1.3 System of Units

As any quantity can be expressed in whatever way you like, it is sometimes easy to become confused as to what exactly or how much is being referred to. This is particularly true in the field of fluid mechanics. Over the years many different ways have been used to express the various quantities involved. Even today different countries use different terminology as well as different units for the same thing - they even use the same name for different things,
e.g. an American pint is 4/5 of a British pint!

1.3.1 Dimension and Units

Dimension = A dimension is the measure by which a physical variable is expressed quantitatively.

Unit = A unit is a particular way of attaching a number to the quantitative dimension.

Thus length is a dimension associated with such variables as distance, displacement, width, deflection, and height, while centimeters or meters are both numerical units for expressing length.

1.3.2 The SI System of units

The SI system consists of six primary units, from which all quantities may be described. For convenience secondary units are used in general practice, which are made from combinations of these primary units.

1.3.3 - Primary Units

The SI system consists of six primary units, from which all quantities may be described. For convenience secondary units are used in general practice, which are made from combinations of these primary units.

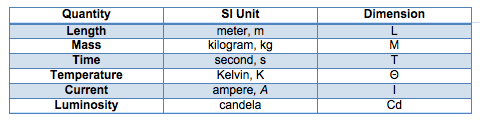
In fluid mechanics we are generally only interested in the top four units from this table.
Notice how the term 'Dimension' of a unit has been introduced in this table. This is not a property of the individual units, rather it tells what the unit represents. For example, a meter is a length which has a dimension L but also, an inch, a mile or a kilometer are all lengths so have dimension of L.

(The above notation uses the MLT system of dimensions, there are other ways of writing dimensions)

1.3.4 - Derived Units

There are many derived (secondary) units all obtained from combination of the above primary units. Those most used are shown in the table below:

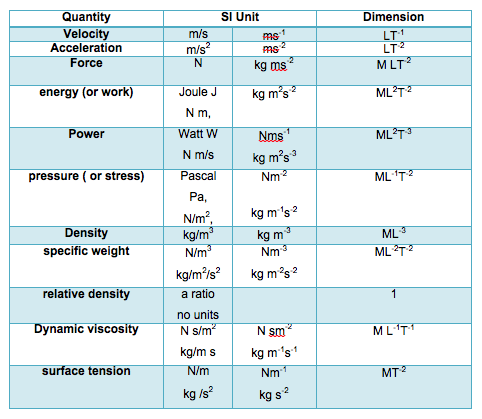
The above units should be used at all times. Values in other units should NOT be used without first converting them into the appropriate SI unit.

1.3.5 - Dimensional Analysis

The fundamental quantities mainly relevant to fluid mechanics are Mass, Length and Time. All other quantities can be expressed in terms of them (e.g. velocity = length/time). The unit schemes give a way of measuring these quantities. All equations must be dimensionally consistent

dim(X) = dim(Y )

The fundamental mass M, length L and time T constituents that make up X and Y must be the same. e.g.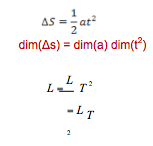

Since the LHS and RHS have the same dimensions it is possible for the equation to be correct.
It is only possible to add or subtract two quantities if they have the same dimension (e.g. you can’t add apples and oranges). The equation can only be true if A and B dimensions are the exact same:

X = A + B
dim(X) = dim(A) + dim(B)

Recommendation from the Module Team:
In working with problems with complex or mixed system units, at the start of the problem convert all parameters with units to the base units being used in the problem, e.g. for S.I. problems, convert all parameters to kg, m, & s. Then convert the final answer to the desired final units.

1.4 Fluids

There are two aspects of fluid mechanics which make it different to solid mechanics:

1. The nature of a fluid is much different to that of a solid
2. In fluids we usually deal with continuous streams of fluid without a beginning or end. In solids we only consider individual elements.

As previously stated that liquid and gas are called fluids and are in contrast to solids they lack the ability to resist deformation. To appreciate this fundamental difference between solids and fluids let us subject block of a solid and block of a fluid to a shearing forces and observe their different behaviour.
Behaviour of a solid when subjected to a tensile force

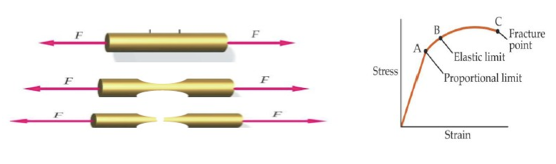
If a solid body is subjected to forces that tend to stretch, compress or shear the object, its shape changes, reaching a new status of equilibrium between external and internal forces. If the object returns to its original shape when the external forces are removed, it is said to be elastic. Most objects are elastic for forces up a certain maximum, called the elastic limit. If the acting forces exceed the elastic limit the object remains permanently deformed or it is fractured. A solid can resist a deformation force while at rest, this force may cause some displacement but the solid does not continue to move indefinitely.

Behaviour of a fluid when subjected to a shearing force

Consider two flat plates of infinite length placed a distance h apart as shown in Figure below. The lower plate is fixed while the upper plate is allowed to move.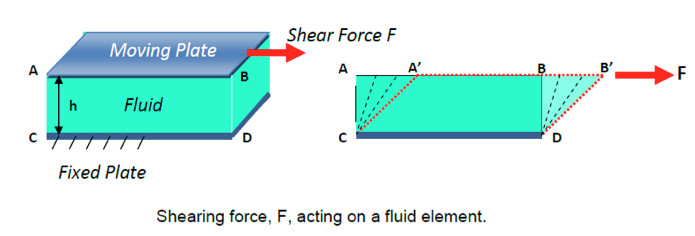

The deformation is caused by shearing forces which act tangentially to a surface. Referring to the figure above, we see the force F acting tangentially on a rectangular element ABDC. This is a shearing force and produces the (dashed lined) rhombus element A’B’DC. Because a fluid cannot resist the deformation force, it moves, it flows under the action of the force. Its shape will change continuously as long as the force is applied.
This is a fundamental difference between solids and fluids and hence is used as a base for the definition of a fluid:

A fluid is a substance which deforms continuously, or flows, when subjected to shearing forces however small it may be.

and conversely this definition implies the very important point that:

If a fluid is at rest there are no shearing forces acting. All forces must be perpendicular to the planes on which they are acting.

1.5 Fluid Properties

Solids, liquids and gases are all composed of molecules in continuous motion. However, the arrangement of these molecules, and the spaces between them, differ, giving rise to the characteristics properties of the three states of matter. In solids, the molecules are densely and regularly packed and movement is slight, each molecule being strained by its neighbors. In liquids, the structure is loser; individual molecules have greater freedom of movement and, although restrained to some degree by the surrounding molecules, can break away from the restraint, causing a change of structure. In gases, there is no formal structure, the spaces between molecules are large and the molecules can move freely.

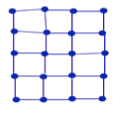
In a solid the atoms are tightly bound by intermolecular forces.

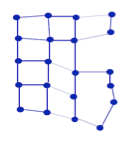
In a liquid the intermolecular forces keep the atoms close together. But, lack of long range order with disruption of molecular forces makes it possible for groups of atoms to slide past each other.

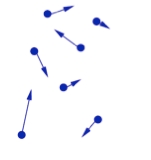
In a gas the molecules can move independently of each other.

Continuum Hypothesis

In this course, fluids will be assumed to be continuous substances, and, when the behaviour of a small element or particle of fluid is studied, it will be assumed that it contains so many molecules that it can be treated as part of this continuum. Quantities such as velocity and pressure can be considered to be constant at any point, and changes due to molecular motion may be ignored. Variations in such quantities can also be assumed to take place smoothly, from point to point.

1.5.1 Density

There are three ways of expressing density:

a. Mass density (ρ):

The fluid mass density (ρ) is one of the primary fluid properties. For a fluid, the mass density is the mass m per unit volume V, so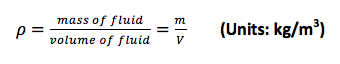

b. Specific Volume (v):

The specific volume is the volume per unit mass and is the reciprocal of the density. Specific volume is mainly used in thermodynamics.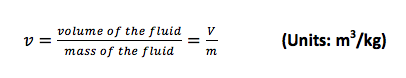

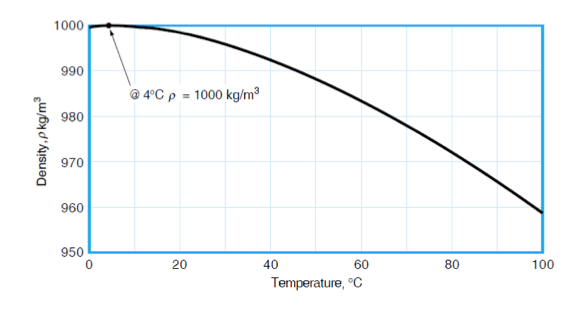
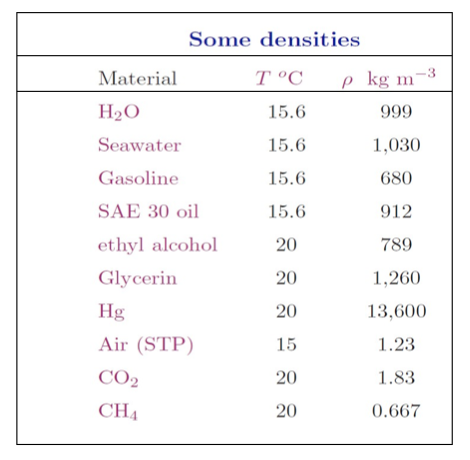
Temperature and pressure do not have much effect on the density of liquids as shown below for the density of water, however they have a huge effect on gases’ density. The density of water is 1000 kg/m3 at 4oC and about 958 kg/m3 at 100oC at atmospheric pressure.

c. Specific Weight (ω):

The specific weight (ω) of a fluid is designated as the weight force per unit volume.

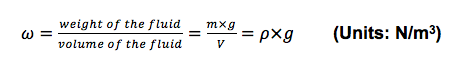
Because the weight (a force), W, related to its mass, m, by Newton’s second law of motion in the form

W = m × g

In which g is the acceleration due to the local force of gravity. The specific weight of water is approximately 9.80 kN/m3

Relative Density (RD):

The relative density of a fluid is the ratio of the fluid mass density to the mass density of water at a specific temperature. For solids and liquids this standard mass density is the maximum mass density for water (which occurs at 4oC) at atmospheric pressure. The reference temperature is usually 4oC since ρ is largest here.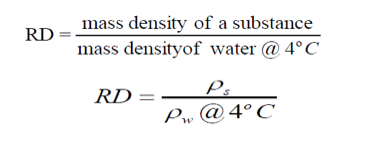

The specific density is a ratio of densities so it is dimensionless.

1.6 Pressure

What is pressure?

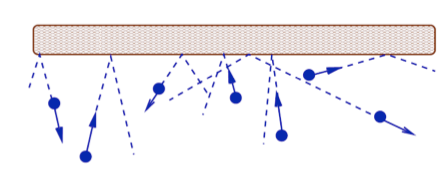
The pressure force arises due to the continual transfer of momentum from individual molecules during collisions with the walls. The SI unit for pressure is the Pascal Pa and as it is a stress 1 Pa = 1 N/1 m2. The pressure force is an example of a stress, i.e. a force that is applied over an area. The pressure force acts in a direction perpendicular to the surface. Hence it is convenient to work in terms of pressure, p, which is the force per unit area.

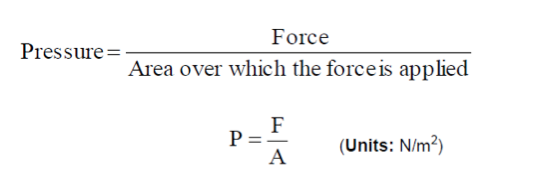
Units: Newtons per square meter, N/m2, kg/m s2 (kg m-1s-2). Also known as a Pascal, Pa, i.e. 1 Pa = 1 N/m2.
Also frequently used is the alternative SI unit the bar, where 1bar = 105 N/m2.
Standard atmosphere = 101325 Pa = 101.325
kPa 1 bar = 100 kPa (kilopascals)
1 mbar = 0.001 bar = 0.1 kPa = 100 Pa

Uniform Pressure: If the pressure is the same at all points on a surface, we call it uniform pressure.

Pressure definitions

There are 3 different working definitions for pressure. These are absolute, gauge or differential pressure.

The absolute pressure is the force per unit area that the molecules inside a chamber exert on the chamber walls. Always positive.

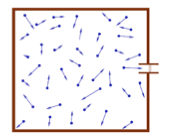
The chamber is immersed in the atmosphere. The gauge pressure is the difference between the absolute pressure and the atmospheric pressure. Can be negative if pressure in chamber is less than atmosphere.

The differential pressure refers to the pressure between two different chambers.

Week1 Activities 1-4
4 activity with randomized numbers and tasks using MapleTA