01
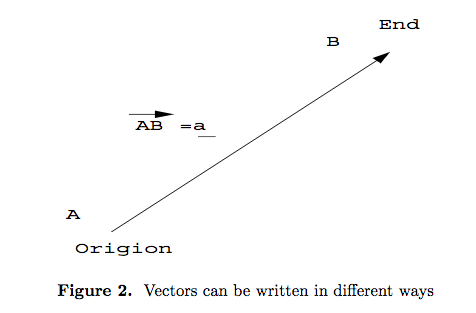
  • It is important when writing vectors to distinguish them from scalars, and so various notations are used. In Fig. 2 we can write the vector as $\overrightarrow{ AB}$, in this figure the point A is called origin and the point B is referred to its end. In handwriting it is customary to underline the vectors when it is shown by only one word, say $\underline a$ .

    BASIC CONCEPTS OF VECTORS


    Introduction
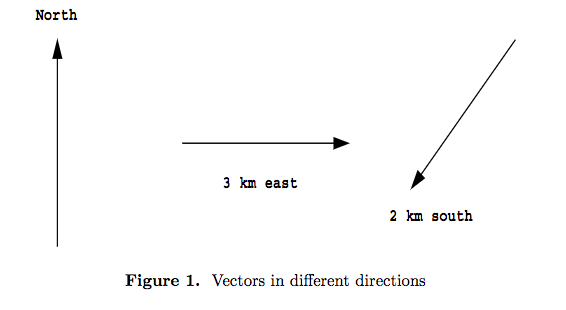
    In engineering, frequently reference is made to physical quantities, such as speed, time, length. It is usefu l to separate physical quantities into two types. Quantities of first type are known as scalars . These can be fully described by a single number called magnitude. Mass, time,length are scalar quantities. Other quantities like velocities, forces, in which direction as well as the magnitude is important, are called vectors. It is customary to present a vector by a directed line segment whose direction represent the direction of the vector and whose length(in terms of some chosen unit of length) represent the magnitude.
    Following are vectors

    Vectors in different directions
  • Vector $\overrightarrow{ AB}$ and $\overrightarrow{ BA}$ have same magnitude and different directions, they are not equal (Fig.3).

    The negative vector has the opposite direction

    Equal vectors


    We say that two vectors are equal provided that they have same di- rection and the same magnitude. We shall ordinarily deal with free vectors, meaning that a vector is free to move about under parallel displacements.

    Vectors can be written in different ways

  • Multiplication of a vector by a scala


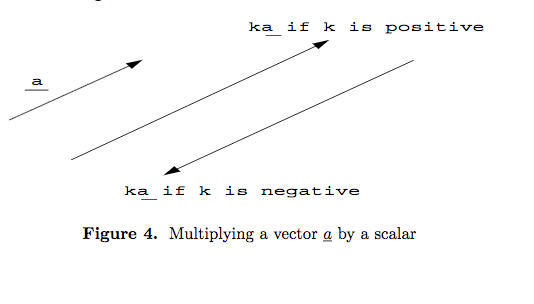
    If k is any scalar and $\underline a$ is any vector then $k\underline a$ is a vector whose magnitude is k times of the vector $\underline a$. Direction of this vector is same as a if k is positive and it is in the opposite direction of $\underline a$ if k is negative. This is shown in Fig. 4.

    Vectors can be written in different ways
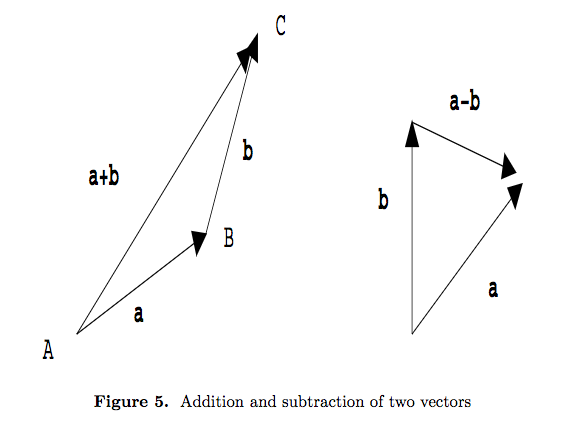
  • Multiplying a vector by a scalar
    Thus we have   $\underline a=\overrightarrow{ AB},~~~\underline b=\overrightarrow{ AC}$$
    and   $\underline a-\underline b=-\underline b+\underline a=\overrightarrow{ CA}+\overrightarrow{ AB}=\overrightarrow{ CB}$

    Addition and subtraction of vectors: Geometrical form


    Two vectors $\underline a$ and $\underline b$ are added by drawing a vector $\underline a$ ,say from A to B in figure 5, and then a vector equal to $\underline b$ starting from the terminal point of $\underline a$; thus $\underline b$=\overrightarrow{ BC}$$ in figure 5. The sum $\underline a$+$\underline b$ is then the vector from the starting point A to the terminal point C of $\underline b$

    Multiplying a vector by a scalar
    $$\underline a=\overrightarrow{ AB},~~~\underline b=\overrightarrow{ BC}$$
    \underline a+\underline b=\overrightarrow{ AB}+\overrightarrow{ BC}=\overrightarrow{AC}$$

    To subtract one vector $\underline b$ from another vector $\underline a$ geometrically, we draw both from a same origin and then draw the vector from the tip of $\underline b$ to the tip of a (see figure 5).

  • Resultant of two forces acting upon a body


    A force $\underline{F}_1$with he magnitude 5N acts on a body vertically downwards, and a force$\underline{F}_2$of 2N acts horizontally to the right, given in figure 6.

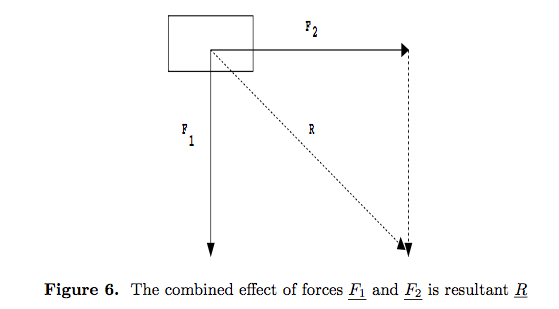
    The combined effect of forces is resultant R

    Addition of these forces known as resultant force.

    $\underline R=\underline {F}_1+\underline {F}_2$

    The resultant force acts at angle of θ where tan θ=5/2, so that θ≈68.2o, with the magnitude of $\sqrt{29}$.

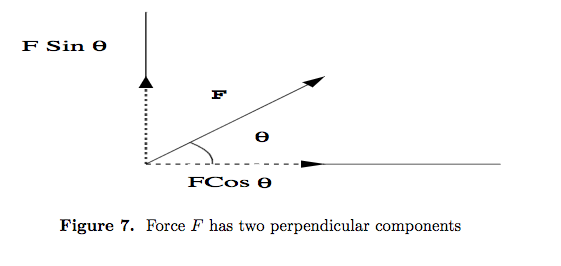
  • Resolving a force into two perpendicular directions


    Consider the force $\underline F$ in figure 7. This force can be replaced by two orthogonal forces as shown. It can easily be shown that the vertical force has magnitude $\underline F_y$=$\underline F$sin θ and horizontal force has magnitude $\underline F_x$=$\underline F$cos θ.

    Force F has two perpendicular components

  • The unit vector


    The unit vector of the vector $\underline a$ is a vector in the same direction of $\underline a$ with the length equal to 1 and it is represented by \underline{\hat{a}}. Hence it can be defined as
    \hat{\underline{a}}={\underline{a}\over |\underline{a}|}

  • Position vector


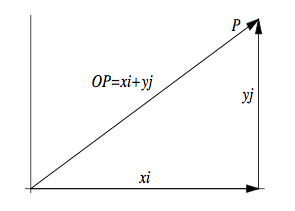
    If P=(x, y) is a point on the plane (shown on the figure below) then the vector\overrightarrow{OP}is called the position vector and can be written as
    \overrightarrow{OP}=x\underline i+y\underline j
    where $\underline i$ and $\underline j$ are unit vectors lie on the x and y-axes, respectively. This representation is called Cartesian or component form of the vector \overrightarrow{OP}.

    Force F has two perpendicular components

    Example 1. Assume P=(8,15) write down the position vector \overrightarrow{OP} in the Cartesian form, and then determine the unit vector in the direction of \overrightarrow{OP}

    r:=\overrightarrow{OP}=8\underline i+15\underline j       \underline {\hat r}={\underline r\over |\underline r|}={8\underline i+15\underline j\over 17}

    where   \underline r|=\sqrt{8^2+15^2}=17and it is called the length of the vector which is described below.

  • Addition and subtraction of two vectors: Component’s form


    If two vectors $\underline a$ and $\underline b$ are given in terms of components
    \underline a&=&a_1\underline i+b_1\underline j
    \underline b&=&a_2\underline i+b_2\underline j,
    then
    \underline a\pm\underline b=(a_1\pm a_2)\underline i+(b_1\pm b_2)\underline j

    Example 2.
    If P=(3,4) and P=(−2,5) then

    \overrightarrow{OP}+\overrightarrow{OQ}&=&(3\underline{i}+4\underline{j})+(-2\underline{i}+5\underline{j})\\&=&\underline{i}+9\underline{j}

  • Cartesian components of vectors in 2-dimensional coordinate system


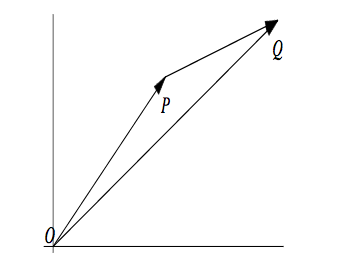
    If P=(x1,y1) and Q=(x2,y2) then referring to the below figure

    \overrightarrow{OP}+\overrightarrow{PQ}=\overrightarrow{OQ}

    Which implies that

    \overrightarrow{PQ}=\overrightarrow{OQ}-\overrightarrow{OP}

    or

    \overrightarrow{PQ}=\overrightarrow{OQ}-\overrightarrow{OP}

    Example 3
    If P(6,4) and Q(8,1), evaluate \overrightarrow{PQ} in component form.
    \overrightarrow{PQ}=(8-6)\underline i+(1-4)\underline j=2\underline i-3\underline j

  • The length of a vector


    The length of vector $\underline a$ s usually denoted by |\underline a|, which is also called magnitude of $\underline a$.
    If  \underline a=x\underline i+y\underline j  then using Pythagoras theorem (figure below) we can obtain
    |\underline a|=\sqrt{x^2+y^2}.

    Example 4
    A force 12 N acts in a direction parallel to \underline a=2\underline i+3\underline j
    Find component form of \underline F

    \underline {\hata}&=&{\underline a\over|\underline a|}\\&=&{2\underline i+3\underline j\over \sqrt{13}}
    \Longrightarrow
    \underline F&=& 12\underline {\hat a}\\&=&{12\over\sqrt{13}}( 2\underline i+3\underline j)
  • Note:
    The following rules apply to the angle \theta

    • if the vector is in the first quadrant then \theta=\tan^{-1}{y\over x}

    • if it is in second quadrant then \theta=180^0-\tan^{-1}|{y\over x}|

    • if it is in third quadrant then \theta=180^0+\tan^{-1}|{y\over x}|

    • if it is in fourth quadrant then \theta=360^0-\tan^{-1}|{y\over x}|

    or
    • if it is in fourth quadrant then \theta=-\tan^{-1}|{y\over x}|

    Example 5
    \underline a=5\underline i-12\underline j. Evaluate the |\underline a| and the angle that \underline a makes with the x-axis. Write down \underline a in polar form.

    The vector is in the fourth quadrant:
    |\underline a|&=&\sqrt{5^2+(-12)^2}=13 \theta&=&360^0-\tan^{-1}|{-12\over5}|=292.6^0=-67.4^0 \Longrightarrow \underline a=(13,-67.4^0)

    Example 6
    Express \underline b=(3, 150^o) in Cartesian (component) form.
    \underline b&=&3\cos(150^0)\underline i+3\sin(150^0)\underline j
    \\&=&-2.6\underline i+1.5\underline j

    Polar form


    If \underline a:=\overrightarrow{OP}=x\underline i+ y\underline jthen angle of this vector with the positive direction of x axis is  \theta=\tan^{-1} (y/x) and the polar form is shown as (|\underline a|,\theta)

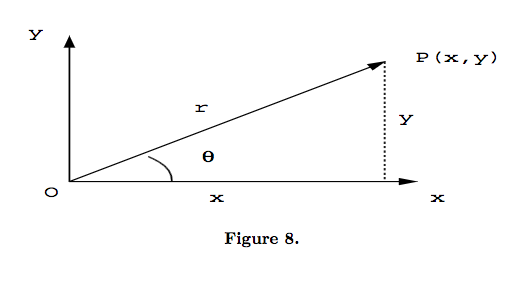
    Polar form image
    It is obvious that

    |\underline a|\cos\theta and \\y&=&|\underline a|\sin\theta




  • The length of any vector  \underline v=a\underline i+b\underline j+c\underline k is determined by applying Pythagoras theorem twice; once to the diagonal of a face of a box (figure 10) and then to the diagonal of the box. In the right angle triangle ABCin (figure 10),

    |\overrightarrow{AC}|=|a\underline i+b\underline j|=\sqrt{a^2+b^2}

    and in the right angle triangle ACD,

    |\overrightarrow{AD}|=\sqrt{|\overrightarrow{AC}|^2+|\overrightarrow{CD}|^2}=\sqrt{a^2+b^2+c^2}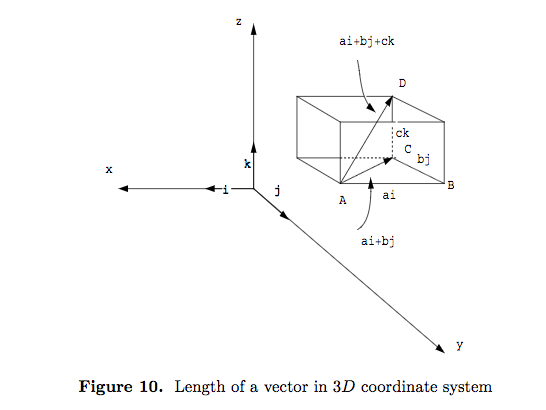
    Example 7
    The position of a helicopter is defined to be 2000m east, 12000m north and 500m high. Thus

    \underline r=2000 \underline i+12000 \underline j+500\underlinek

    Example 8
    If  \underline a=2\underline i+\underline j-3\underline k  and   \underline b=5\underline i-3\underline j+4\underline k  determine:

    1.  \underline a+\underline b

     \underline a+\underline b&=&(2+5)\underline i+(1-3)\underline j+(-3+4)\underline k
    &=& 7\underline i-2\underline j+\underline k


    2.  3\underline b-2\underline a

             3\underline b &=& 15\underline i -9\underline j+12\underline k
             2\underline a &=& 4\underline i +2\underline j-6\underline k
    3\underline b-2\underline a &=& (15-4)\underline i +(-9-2)\underline j+(12+6)\underline k
                   &=& 11\underline i -11\underline j+18\underline k

    3. |\underline a|+|\underline b|

    |\underline a+\underline b|=\sqrt{49+4+1}=\sqrt{54}

    4. |\underline a|+|\underline b|

              |\underline a|&=& \sqrt{4+1+9}=\sqrt{14}
              |\underline b|&=& \sqrt{25+9+16}=\sqrt{50}
    |\underline a|+|\underline b|&=&\sqrt{14}+\sqrt{50}

    Vectors in space


    The vectors from the origin to the points (1,0,0), (0,1,0) and (0,0,1) are the basic unit vectors, which we denote them by \underline i, \underline j and \underline k. In this notation a vector from origin to the point P(x, y, z)is simply   \overrightarrow{OP}=x\underline i+y\underline j+z\underline k

    A vector on 3D coordinate system
    If P_1=(x_1,y_1,z_1) and P_2=(x_2,y_2,z_2) are two points in space (figure9) then the vector from P1 to P2 is the vector sum
    \overrightarrow{P_1P_2}=\overrightarrow{P_1O}+\overrightarrow{OP_2}
    Since  \overrightarrow{P_1O}=-\overrightarrow{OP_1}

    then   \overrightarrow{P_1P_2}=\overrightarrow{OP_2}-\overrightarrow{OP_1},

    or  \overrightarrow{P_1P_2}=(x_2-x_1)\underline i+(y_2-y_1)\underline j+(z_2-z_1)\underline k

  • Scalar product of two vectors


    So far we have not defined what is the meaning of multiplication of two vectors. There are two kind of vector multiplication which are significant in physical applications.

    1. The scalar product is denoted by \underline A.\underline B.  This product is also called dot product. The result is a scalar.

    2.The vector product is denoted by \underline Ax \underline B.  The result is a vector.

    The scalar product is defined by the equation  \underline A.\underline B=|\underline A||\underline B|\cos\theta

    where \theta is the angle between the two vectors (0\leq\theta\leq \pi)

    • If two vector are orthogonal,ie.\theta=\pi/2   then   \underline A.\underline B=0

    • Since  \underline i, \underline j and \underline k are mutually orthogonal then \underline i.\underline j=0, \underline i.\underline k=0, and \underline j.\underline k=0

    • Since  |\underline i|=|\underline j|=|\underline k|=1 then  \underline i.\underline i=\underline j.\underline j= \underline k.\underline k=1


    Now we calculate the scalar product of 2 vectors in terms of their components. To calculate the scalar product \underline A.\underline B.in terms of the components of the vectors, we assume (see figure 11)

    \underline A&=&a_1\underline i+a_2\underline j+a_3\underline k
    \underline B&=&b_1\underline i+b_2\underline j+b_3\underline k

    and

    \underline C&=&\underline B-\underline A
    &=&(b_1-a_1)\underline i+(b_2-a_2)\underline j+(b_3-a_3)\underline k.
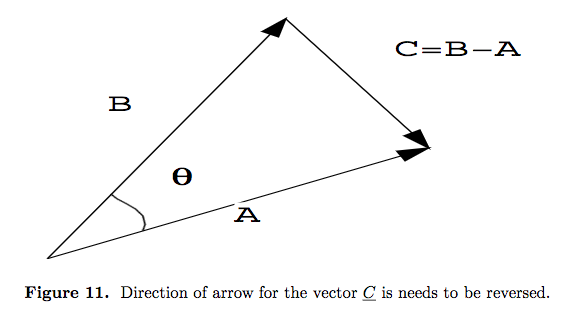
    Direction of arrow for the vector C is needs to be reversed.
    Now we apply the law of cosines to the triangle whose sides are vectors   \underline A,~\underline B and \underline C, then we obtain |\underline C|^2&=&|\underline A|^2+|\underline B|^2-2|\underline A||\underline B|\cos\theta \\ |\underline A||\underline B|\cos\theta &=& {|\underline A|^2+|\underline B|^2-|\underline C|^2\over 2}

    Evaluating the terms in the right hand side of the above equation in terms of components of  \underline A.\underline B implies that  \underline A.\underline B=a_1b_1+a_2b_2+a_3b_3

    Example 9.
    Vectors are drawn from the origin O to the two points  A=(1,-2,-2) and  B=(6,3,-2)  

    Find the angle between AOB.

    \overrightarrow{OA}&=&\underline i-2\underline j-2\underline k\\ \overrightarrow{OB}&=&6\underline i+3\underline j-2\underline k\\ \cos\theta&=&{\overrightarrow{OA}.\overrightarrow{OB}\over |\overrightarrow{OA}||\overrightarrow{OB}|}\\ &=&{6-6+4\over \sqrt{9}\times \sqrt{49}}={4\over 21}

    \Longrightarrow
    \theta=\cos^{-1}{4\over 21}\approx 70^0

    Example 10.
    Show that  \underline N=a\underline i+b\underline j is perpendicular to the line ax+by+c=0.

    Assume the two points A=(x_1,y_1) and B=(x_2,y_2) lie on the line, then \overrightarrow{AB}=(x_2-x_1)\underline i+(y_2-y_1) \underline j

    The vector \underline N is perpendicular to the line if 
    \overrightarrow{AB}.\underline N=0 ~~~~\mbox{i.e}~~~a(x_2-x_1)+b(y_2-y_1)=0

    Now since A and B are on the line hence:
    ax_1+by_1+c&=&0
    ax_2+by_2+c&=&0
    Subtracting the above equations \Longrightarrow
    a(x_2-x_1)+b(y_2-y_1)=0


    Example 11
    If  \underline a=x\underline i+y\underline j+z\underline k 
    then
    \underline a.\underline a=x^2+y^2+z^2  
    thus
    \underline a.\underline a=|\underline a|^2


    Example 12
    Find the angle between \underline a=2\underline i +\underline j-2\underline k$ and $\underline b=4\underline i +3\underline j+5\underline k 
    \cos\theta&=&{\underline{a}.\underline{b}\over |\underline{a}||\underline{b}|}  
    thus
    =&{1\over 3\sqrt{50}} \Longrightarrow
    \theta&=&\cos^{-1}{1\over 3\sqrt{50}}\approx 87.3^0


    Example 13
    Find angles which \underline r=2\underline i-4\underline j+3\underline k  makes with the coordinate axes

    \underline r.\underline i&=&|\underline r||\underline i|\cos\theta_x\\ 2&=&\sqrt{29}\cos\theta_x \Longrightarrow\\ \theta_x&=&\cos^{-1}{2\over \sqrt{29}}\approx 68.2^0 \\
    \underline r.\underline j&=&|\underline r||\underline j|\cos\theta_y\\ -4&=&\sqrt{29}\cos\theta_y \Longrightarrow\\ \theta_y&=&\cos^{-1}{-4\over \sqrt{29}}\approx 137.97^0
    \underline r.\underline k&=&|\underline r||\underline k|\cos\theta_z\\ 3&=&\sqrt{29}\cos\theta_z\Longrightarrow\\ \theta_z&=&\cos^{-1}{3\over \sqrt{29}}\approx 56.15^0