10
-
10.1 - Energy Transfer by Heat
- When you put a cold spoon into a cup of hot coffee, the spoon warms up and the coffee cools as they approach thermal equilibrium. The interaction that causes these temperature changes is fundamentally a transfer of energy from one substance to another. Energy transfer that takes place solely because of a temperature difference is called heat flow or heat transfer, and energy transferred in this way is called heat.
Heat is a form of energy that can cross the boundary of a system. (Note that the type of system is not specified as heat can be transferred to both closed and open systems). As such it is analogous to work but, whereas work is easier to visualise because it is associated with physical movement of a piston or a rotating shaft, heat is more difficult to understand.
It is important to note that temperature and thermal energy are not the same thing. The concept of temperature is rooted in qualitative ideas of “hot” and “cold” based on our sense of touch. A body that feels hot usually has a higher temperature than a similar body that feels cold. Temperature is related to the kinetic energies of the molecules of a material. In general this relationship is fairly complex. For heat to be transferred between two points, a temperature difference between those two points must exist. That is, one point must be hotter than the other. Of its own accord, heat flows from regions of higher temperature to regions of lower temperature.
Heat can, therefore, be defined as “the form of energy that is transferred between a system and its surroundings as a result of a temperature difference”. There can only be a transfer of energy across the boundary in the form of heat if there is a temperature difference between the system and its surroundings. Conversely, if the system and surroundings are at the same temperature there is no heat transfer across the boundary.
Strictly speaking, the term “heat” is a name given to the particular form of energy crossing the boundary. However, heat is more usually referred to in thermodynamics through the term “heat transfer” which is consistent with the ability of heat to raise or lower the energy within a system.
There are three modes of heat transfer: Conduction, Convection, and Radiation. All three are different.
Conduction relies on transfer of energy between molecules within a solid or fluid. Metals are very good conductors of heat. Like all substances, metals are made up of tiny particles. The particles in all solid substances are vibrating. When you heat a solid object, its temperature increases causing the particles vibrate faster and bump into each other. The vibrations are passed from particle to particle along the object until the whole object is hot.
- Heat Transfer by Conduction 📹
- Convection relies on movement of a fluid. Liquids and gases are fluids. The particles in these fluids can move from place to place. Convection occurs when particles with a lot of heat energy in a liquid or gas move and take the place of particles with less heat energy. Heat energy is transferred from hot places to cooler places by convection.
- Heat Transfer by Convection 📹
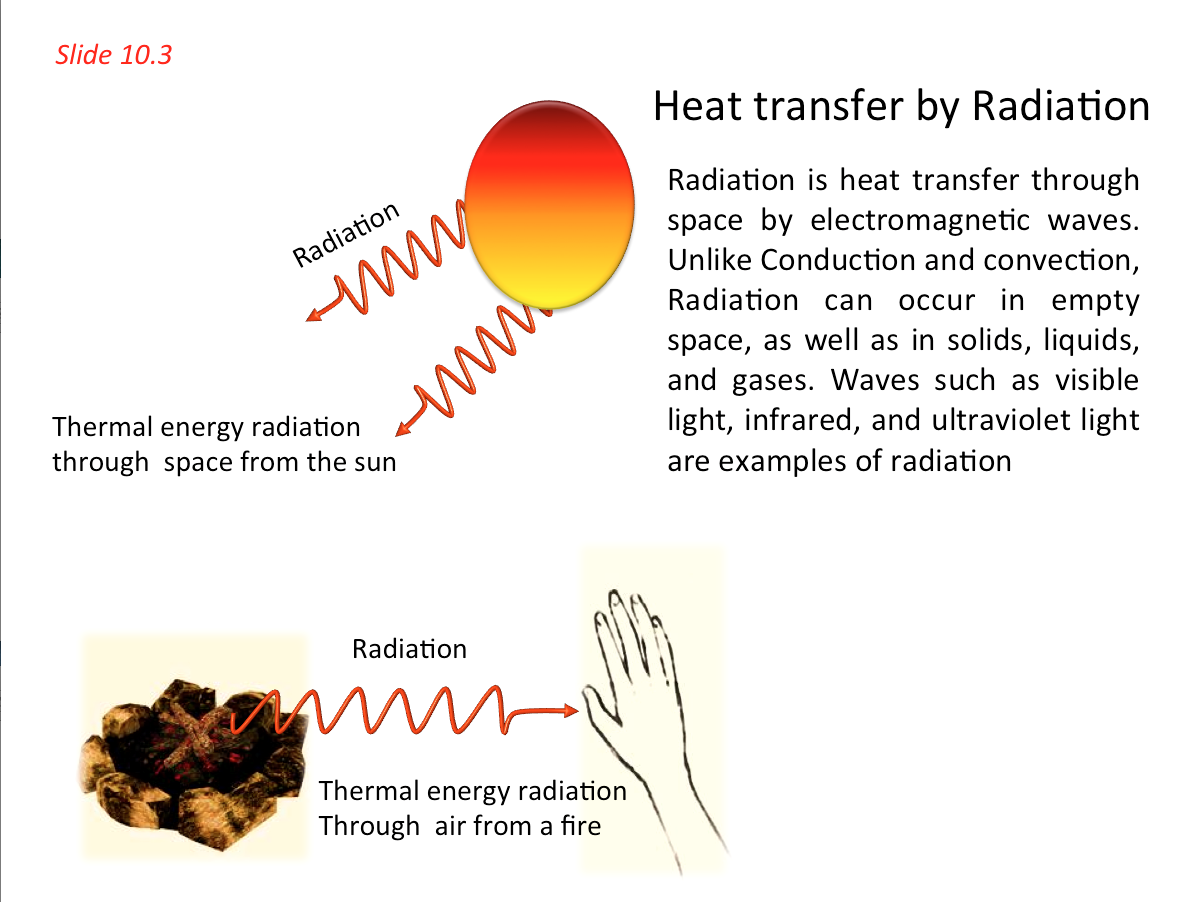
- Radiation is a form of electromagnetic energy transmission and is independent of the substance between the emitter and receiver of such energy. Unlike Conduction and convection, Radiation can occur in empty space, as well as in solids, liquids, and gases. Waves such as visible light, infrared, and ultraviolet light are examples of radiation
- Heat Transfer by Radiation 📷
- However, all three modes of heat transfer rely on a temperature difference for the transfer of energy to take place. If the temperature of the surroundings is higher than the fluid in the system then the transfer of energy is positive and there is said to be “heat addition” to the system. If the fluid in the system is at a higher temperature than the surroundings, then there is “heat rejection” from the system.
- When you put a cold spoon into a cup of hot coffee, the spoon warms up and the coffee cools as they approach thermal equilibrium. The interaction that causes these temperature changes is fundamentally a transfer of energy from one substance to another. Energy transfer that takes place solely because of a temperature difference is called heat flow or heat transfer, and energy transferred in this way is called heat.
-
10.2 - Energy transfer by Work
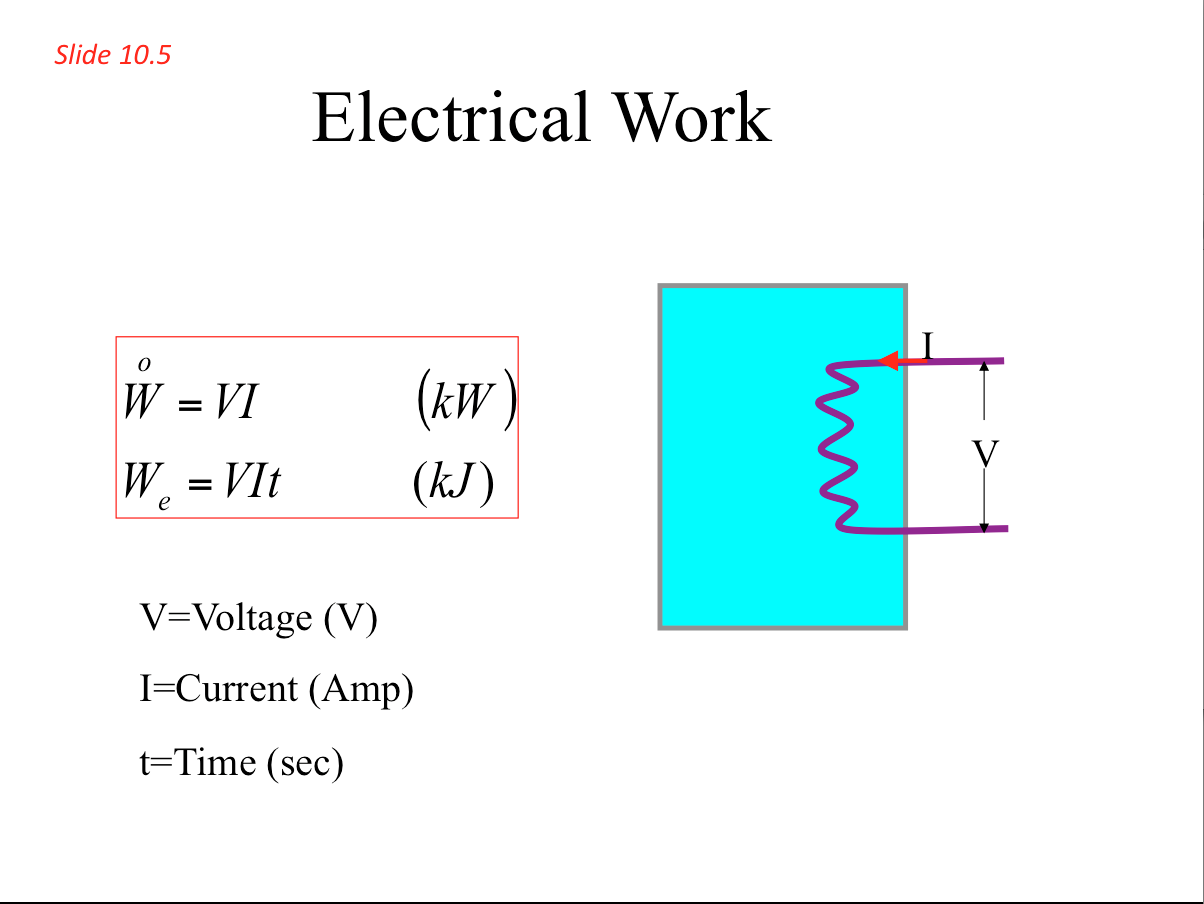
- The transfer of work between a system and its surroundings can be carried out in many forms, including mechanical, electrical and magnetic work.
- Energy Tranfer by Work 📹
- Electrical Work 📷
- Work is a mechanical form of energy that can cross the boundary of a closed system. It is associated with a force (F) moving through a distance (S):
Where F is the force on a body displaced by a distance S.
This relationship is important in thermodynamics. In the present section it is used to evaluate the work done in the compression or expansion of a fluid.
- Definition of Mechanical Work 📹
-
10.2.1 - Work across a static boundary
- A typical example of a closed system with a static boundary is a fluid inside a rigid sealed container. Work can cross the boundary by means of a rotating shaft that drives a propeller or paddle wheel inside the container, as shown below.
- Mechanical Work: Shaft work 📹
- Mechanical Work: Spring work 📷
- Example: A transmission shaft in a car engine rotates at a rate of 5000 revolution per minute (rpm).
Given that the applied torque is 250 N.m, determine the power transmitted through the shaft.
Solution: The shaft power is directly determined from the following equation
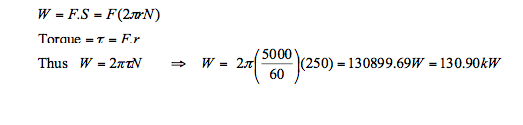
- Self Assessment
- Air is supplied to a train tunnel using a shaft-driven air-handling fan rotating at the rate of 200 rpm. The fan is operated by a belt running on a pulley of 250mm diameter. Given that the total force acting on the pulley is 3500N, determine the power transmitted in kW.
- Self-assessment Solution 📹
- A typical example of a closed system with a static boundary is a fluid inside a rigid sealed container. Work can cross the boundary by means of a rotating shaft that drives a propeller or paddle wheel inside the container, as shown below.
-
10.2.2 - Work across a moving boundary
- A typical example of a closed system with a movable boundary is a cylinder and piston assembly. As the assembly moves the work done is due to the force on the piston, as a result of the pressure of the fluid within the system, moving through a distance.
Consider the situation shown in figure below. One kg of fluid (as a gas as this is probably the easiest to visualise), is contained within a cylinder having a frictionless piston. The piston is loaded with two weights. With all the weights in position, as shown in the first figure, the pressure inside the system is P. Under these conditions it can be assumed that the system is in equilibrium and there is no heat transfer between the system and the surroundings.
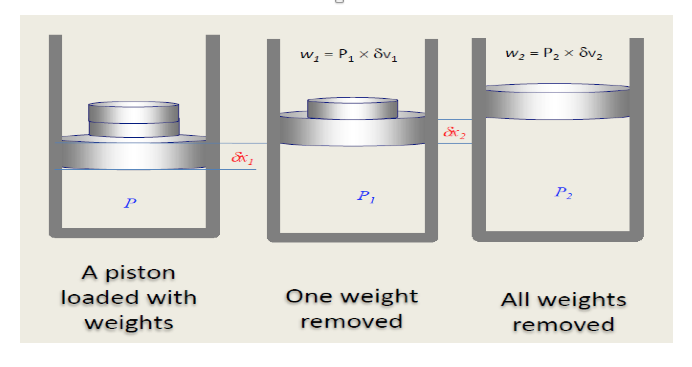
The removal of the first weight will cause a sudden drop in pressure to P1 and the piston to move. Once the system has regained a state of equilibrium the piston will have moved through a distance δx1. As shown in the middle figure. Similarly, removal of the second weight will cause a drop in pressure to P2 and a movement of the piston by δx2, as shown in the last figure. Movement of the piston causes work to be done and ignoring the pressure of the surroundings, the work done by removing weight 1 is given by: w = P1 × A × δx1 = P1 × (Aδx1) where A is the cross-section area of the piston.
Now (Aδx1) is a change in volume and since the system contains unit mass, this is a change in specific volume δv1. Hence, the work done by removing weight 1 is given by
w1 = P1 × δv1
Similarly for weight 2, the work is
w2 = P2 × δv2
The expansion processes for the removal of the weights is shown on a pressure-specific volume diagram in Figure 2.4. If, for each individual process, the system is at equilibrium then the total work for all processes is the sum of all the individual works.
w = w1+w2 + ....
= P1δv1+P2δV2 .....
If the incremental weights and therefore, the resultant change in volume were made infinitesimally small, the work for each incremental change in pressure would be
δW = PdV
With such small changes each individual process becomes merged into one continuous process. For the whole process, as shown in Figure below, the total work is the integration of all the infinitesimal changes between the initial state, point 1 and the final state, point 2.
Since the original series of processes, portrayed in Figure above are reversible it is assumed that the continuous process, shown in Figure above, is also reversible. In fact, the above is only valid for a reversible process. If there was friction between the piston and cylinder then some part of the work would be used in overcoming that friction and that actual work done would be less.
Just as for the original series of processes, the work is the area under the curve from point 1 to point 2. It can, therefore, be concluded that for a reversible process, within a closed system, the area under a process curve on a pressure-specific volume diagram is equal to the work done. This is true irrespective of whether there is heat transfer across the boundary or not. The principle holds true if the mass of fluid inside the closed system is greater, or less, than 1kg. By multiplying both sides of equation
by the mass of fluid m it can be shown that the actual work done is equal to the area under the process curve on a pressure-volume (P-v) diagram. Under these circumstances the actual work done is expressed in joules (or kJ).
A typical example of a closed system 📹
A typical example of a closed system with a movable boundary 📹
Mechanical work: Moving Boundary work 📹
Analysis of displacement work 📹
Analysis of displacement work - fluid under constant pressure 📹
Displacement work 📹
Moving Boundary work 📹
- A typical example of a closed system with a movable boundary is a cylinder and piston assembly. As the assembly moves the work done is due to the force on the piston, as a result of the pressure of the fluid within the system, moving through a distance.
-
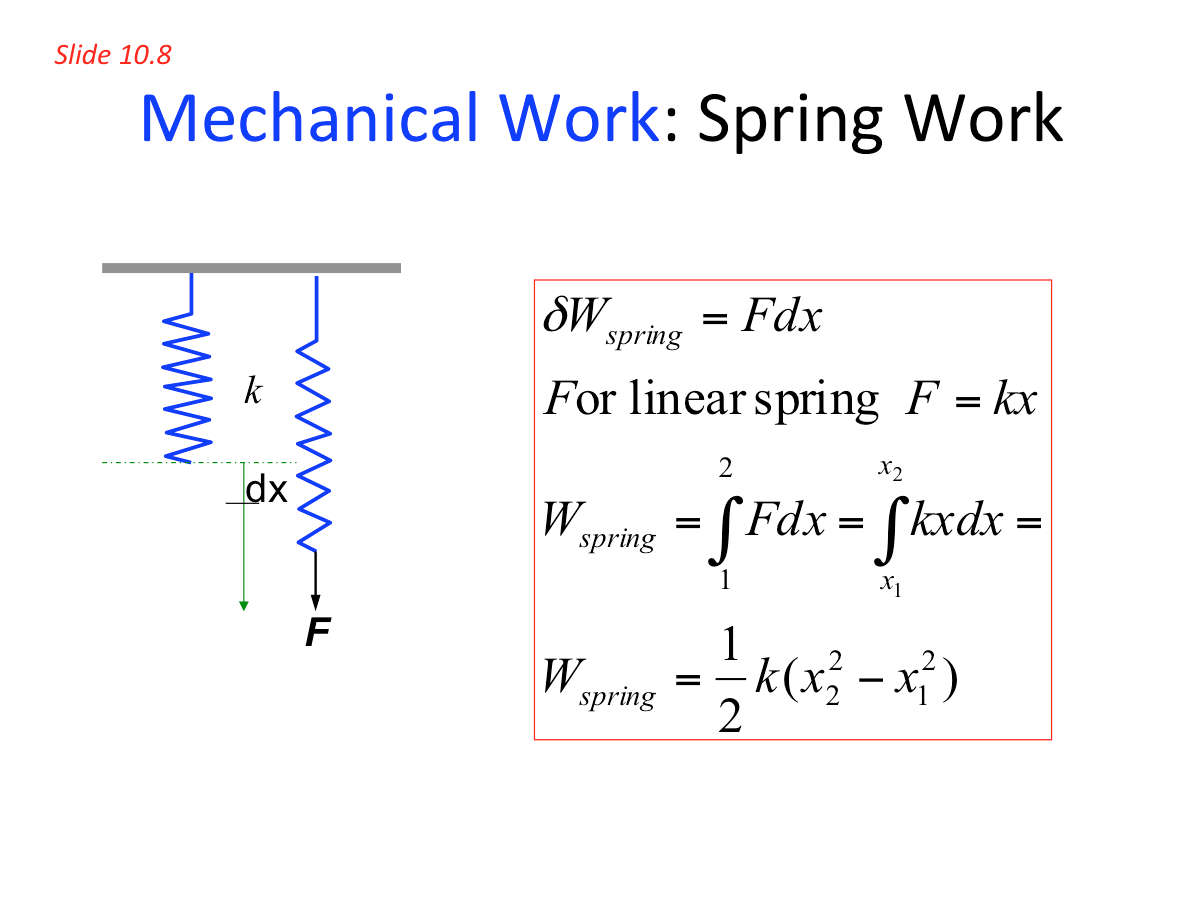
10.2.3 - Other Types of Work
- Displacement work ( ) is fundamental in most of thermodynamic systems. As a result we will be concentrating on understanding this type of work and shaft work. However, students should be aware of other kinds of work such as an elastic wire or to compress a spring, magnetic work and electrical work.
-
10.3 - Energy Equation and First Law of Thermodynamics
- The first law of thermodynamics - the law of conservation of energy - when applied to any system, open or closed, is a statement of “energy balance”, such as
(net amount of energy added to system) = (net increase in stored energy of system)
OR
With both open and closed systems, energy can be added to the system or taken from it in the form of heat and work.
- Application of general energy equation to a closed system 📹
- In section 9 we introduced the different forms of energy associated with a substance and its state. These include the internal energy U, kinetic energy KE and potential energy PE. The total energy possessed by a mass can be written as
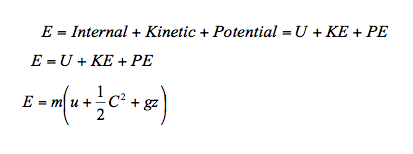
In many thermodynamic processes we are interested in the energy change between the initial and the final states and not the intermediate states at which the process proceeds. The energy equation for finite change become
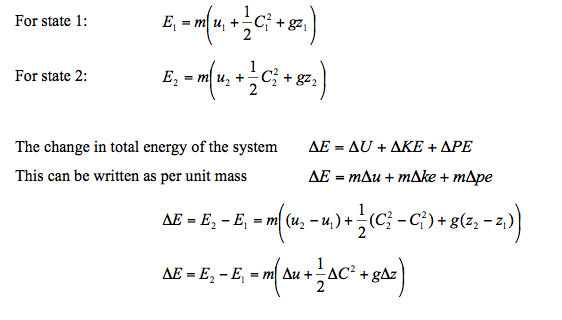
- The first law of thermodynamics - the law of conservation of energy - when applied to any system, open or closed, is a statement of “energy balance”, such as
-
10.3.1 - Energy balance for Closed Systems
- As mentioned, the first law of thermodynamics is a statement of the principle of conservation of energy. It asserts that the net flow of energy across the boundary of a system is equal to the change in energy of the system. Because we are discussing only transients, we need consider only two types of energy flow across a boundary - work done
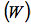on or by the system and heat transferred 
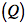to or from the system. The energy balance can be expressed as
Energy Balance for closed system 📷
- The First Law of Thermodynamics:
Therefore, the first law for closed systems executing a cyclic process is as follows: during any thermodynamic cycle a system undergoes the cyclic integral of the heat proportional to the cyclic integral of work. Hence,
This experimentally verified equation is an accurate form of the first law, but it is not the most convenient. Note that this equation is called a law; that is guaranteed to be correct for all situations. If you doubt the universal accuracy of this statement, the only rebuttal one can make is that in all its forms and applications, it has not been found to be in error.
Equation 2-2 applies only to closed-system cyclic processes. Let us extend this line of reasoning to non-cyclic processes (the change of state of a system). The non-cyclic form may be deduced from the cyclic form directly. To do this, consider a change in state of the system from state 1 to state 2 by path A and then back to state 1 by path B (see Figure below)
Cyclic Process 📷
Important Note: The above discussion presents two different paths for the system to follow between the same starting and ending points, and the change in internal energy for each is the same — This proves that ΔU (internal energy) is independent of path of the process and only depend on the initial and final states of the system. Hence ΔU is a thermodynamic property. Note that Q andW are NOT thermodynamic properties and their value depend on the path of the process selected.
Example
Express the change in internal energy of a system when;
(i) No heat is absorbed by the system from the surroundings, but work (W) is done on the system. What type of wall does the system have?
(ii) No work is done on the system, but amount of heat (Q) is transferred from the system to the surroundings. What type of wall does the system have?
(iii) Amount of work is done by the system and Q amount of heat is supplied to the system. What type of system would it be?
Example
An insulated rigid vessel fitted with paddle wheel contains 1.45 kg of water, initially with a specific internal energy of 192kJ/kg. The paddle wheel transfers energy to the water by means of rotating with a torque of 0.3Nm and completes 1000 rpm. Given that there is no significant change in the kinetic or potential energy of the water, determine the final value of specific internal energy.
Example
Consider a piston-cylinder device contains 10 kg of water vapour (steam). Heat is added causing the system to undergo an expansion process from initial state (state 1), where the specific internal energy is 2631kJ/kg, to final state (state 2), where the specific internal energy is 2798kJ/kg. During the process, 217kJ of heat is transferred to the steam and 70kJ lost from the side walls of the cylinder. Also a paddle wheel transfers 50kJ energy to the steam in the form of work. Given that there is no significant change in the kinetic or potential energy of the steam, determine the amount of work transfer, in kJ, from the steam to the piston during the expansion process.
Example
A closed system undergoes a process from state 1 to state 2 in which there is 219 kJ of heat transferred from the surroundings to the system. The internal energy is increased by 129 kJ. To restore the closed system to its initial state (state 2 to state 1), 90kJ of work is done on the system. Given that there is no significant change in the kinetic or potential energy of the steam, determine 2Q1 in kJ.
- As mentioned, the first law of thermodynamics is a statement of the principle of conservation of energy. It asserts that the net flow of energy across the boundary of a system is equal to the change in energy of the system. Because we are discussing only transients, we need consider only two types of energy flow across a boundary - work done
-
Self-Assessment Questions
- 1. The first law of thermodynamics is the law of
(a) conservation of mass
(b) conservation of energy
(c) conservation of momentum
(d) conservation of heat
(e) conservation of temperature.
2. The first law of thermodynamics states that:
a. matter and energy may be interconverted
b. energy is degraded when it changes form
c. all systems move towards maximum disorder
d. energy is neither created nor destroyed
3. For a simple closed system of constant composition, the difference between the net heat and work interactions is identifiable as the change in
a. enthalpy
b. entropy
c. flow energy
d. internal energy
4. Gas contained in a closed system consisting of a piston cylinder arrangement is expanded. Work done by the gas during expansion is 50kJ.
Decrease of internal energy of the gas during expansion is 30kJ. Heat transfer during the process is
a. -20kJ
b. +20kJ
c. -80kJ
d. +80kJ
5. The specific internal energy of a system containing 2 kg of gas is increased from 120kJ/kg to 180 kJ/kg during a constant volume process.
The required heat transfer is:
a. -120kJ
b. +120kJ
c. -180kJ
d. +180kJ
6. A mass of gas expands from 0.03m3 to 0.06m3 at a constant pressure of 1 MPa and absorbs 84 k J of heat during the process.
The change in internal energy of the gas is
a. 30 k J
b. 54 k J
c. 84 k J
d. None of the above
7. A gas is compressed in a cylinder by a movable piston to a volume one-half its original volume. During the process 300kJ heat left the gas and internal energy remained same.
The work done on gas in Nm will be
(a) 300 Nm
(b) 300,000 Nm
(c) 30 Nm
(d) 3000 Nm
(e) 30,000 Nm.
8. Minimum work in compressor is possible when the value of adiabatic index n is equal to
(a) 0.75
(b) 1
(c) 1.27
(d) 1.35
(e) 2.
9. In a non-flow reversible process for which p = (- 3V+ 15) x 105N/m2, the volume (V) changes from 1 m to 2 m3.
The work done will be about
(a) 100 xl05 J
(b) 1 xl05 J
(c) 10 xl05 J
(d) 10 xl05 kJ
(e) 10xl04kJ
10 . If a gas is heated against a pressure, keeping the volume constant, then work done will be equal to
(a) + v
(b) – ve
(c) zero
(d) pressure x volume
(e) any where between zero and infinity.
11. A gas is compressed in a cylinder by a movable piston to a volume one-half its original volume. During the process 300kJ heat left the gas and internal energy remained same.
The work done on gas in Nm will be
(a) 300 Nm
(b) 300,000 Nm
(c) 30 Nm
(d) 3000 Nm
(e) 30,000 Nm.
Click this link to view answers- 1. The first law of thermodynamics is the law of
(a) conservation of mass
(b) conservation of energy
(c) conservation of momentum
(d) conservation of heat
(e) conservation of temperature.
Ans: b
2. The first law of thermodynamics states that:
a. matter and energy may be interconverted
b. energy is degraded when it changes form
c. all systems move towards maximum disorder
d. energy is neither created nor destroyed
Ans: d
3. For a simple closed system of constant composition, the difference between the net heat and work interactions is identifiable as the change in
a. enthalpy
b. entropy
c. flow energy
d. internal energy
Ans: d
4. Gas contained in a closed system consisting of a piston cylinder arrangement is expanded. Work done by the gas during expansion is 50kJ. Decrease of internal energy of the gas during expansion is 30kJ. Heat transfer during the process is
a. -20kJ
b. +20kJ
c. -80kJ
d. +80kJ
Ans: b
5. The specific internal energy of a system containing 2 kg of gas is increased from 120kJ/kg to 180 kJ/kg during a constant volume process. The required heat transfer is:
a. -120kJ
b. +120kJ
c. -180kJ
d. +180kJ
Ans: b
6. A mass of gas expands from 0.03m3 to 0.06m3 at a constant pressure of 1 MPa and absorbs 84 k J of heat during the process. The change in internal energy of the gas is
a. 30 k J
b. 54 k J
c. 84 k J
d. None of the above
Ans: b
7. A gas is compressed in a cylinder by a movable piston to a volume one-half its original volume. During the process 300kJ heat left the gas and internal energy remained same. The work done on gas in Nm will be
(a) 300 Nm
(b) 300,000 Nm
(c) 30 Nm
(d) 3000 Nm
(e) 30,000 Nm.
Ans: b
8. Minimum work in compressor is possible when the value of adiabatic index n is equal to
(a) 0.75
(b) 1
(c) 1.27
(d) 1.35
(e) 2.
Ans: b
9. In a non-flow reversible process for which p = (- 3V+ 15) x 105N/m2, the volume (V) changes from 1 m to 2 m3. The work done will be about
(a) 100 xl05 J
(b) 1 xl05 J
(c) 10 xl05 J
(d) 10 xl05 kJ
(e) 10xl04kJ
Ans: c
10 . If a gas is heated against a pressure, keeping the volume constant, then work done will be equal to
(a) + v
(b) – ve
(c) zero
(d) pressure x volume
(e) any where between zero and infinity.
Ans: c
11. A gas is compressed in a cylinder by a movable piston to a volume one-half its original volume. During the process 300kJ heat left the gas and internal energy remained same. The work done on gas in Nm will be
(a) 300 Nm
(b) 300,000 Nm
(c) 30 Nm
(d) 3000 Nm
(e) 30,000 Nm.
Ans: b - 1. The first law of thermodynamics is the law of
-
TUTORIAL 10 : THE FIRST LAW OF THERMODYNAMICS
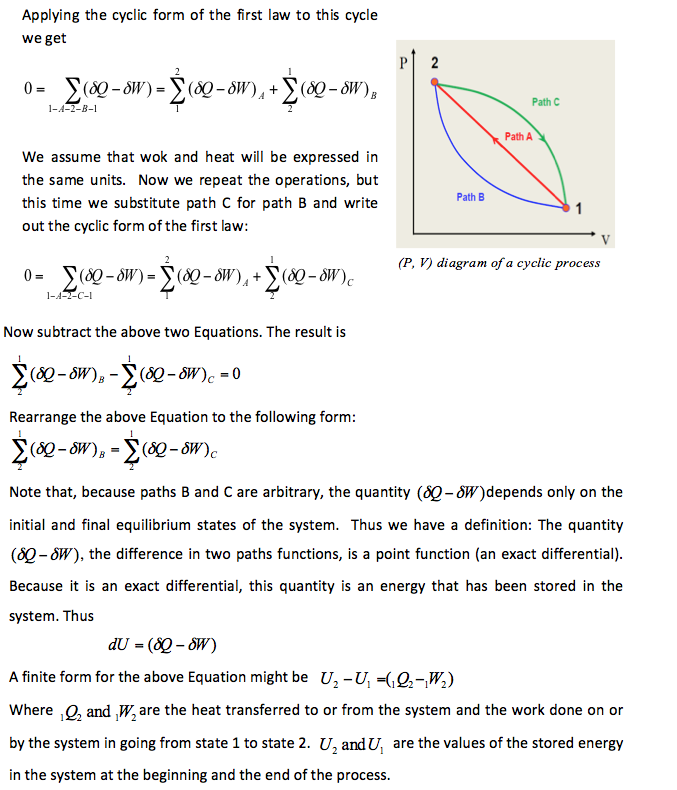
- 1. Each line in the following table gives information about a process of a closed system. Every entry has the same energy units. Fill in the blank spaces in the table.
2. A closed system of mass of 5kg undergoes a process in which there is a heat transfer of 150kJ from the system to the surroundings. The work done by the system is 75kJ. If the initial specific internal energy of the system is 450kJ/kg, determine the final specific internal energy in kJ/kg.
3. A rigid tank contains a hot fluid that is cooled while being stirred by a paddle wheel. The internal energy of the fluid is 800 kJ. During the cooling process, the fluid loses 500kJ of heat, and the paddle wheel does 100kJ of work on the fluid. Determine the final internal energy of the fluid.
4. (a) A closed system which consists of a mass of working fluid, undergoes a process. During the process the heat transfer to the system is 42.2 kJ, and the work transfer from the system is 61,000 N m. Determine the change of internal energy of the system.
(b) If the system were to undergo a process, during which the work transfer from the system was 47,200 N m between the same initial and final states, determine the magnitude and direction of the heat transfer during the process.
5. A piston cylinder containing 2kg of steam, which expands from state-1 (u1=2700 kJ/kg) to state-2 (u2=2650 kJ/kg). During the expansion process the system receives 30kJ of heat. Determine the system work.
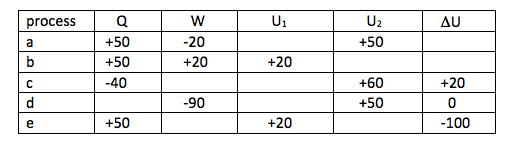
6. An adiabatic (adiabatic means heat transfer is zero) tank contains 10 kg of water. A 110 volt, 0.1 amp motor drives a paddle wheel and runs for 1 hour, as shown in Figure 6.
Determine the change of specific and total internal energy of the water.
7. A vertical piston cylinder assembly containing water is being heated on a stove. During this process 100 kJ of heat is transferred to the water. In the water’s expansion process (because of heat addition), 10 kJ of work done. Also there is 20 kJ of heat loss from the assembly. Determine the water’s change of internal energy as a result of the heat addition process.
8. Fill in the missing data in the table below for a closed system changing from state 1 to state 2. Every entry has the same energy units
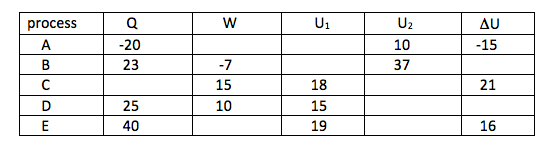
9. A system operates on a two-process cycle. During the first process 50 kJ of heat is added to the system, and the system performs 70 kJ of work. In the second process 50 kJ of work is added to the system.
Determine:
i. the heat transfer during the second process;
ii. the network and the net heat transfer for the cycle.
Click on this link for theTutorial Answer 📷
Tutorial Answers:
- 2. Answer: 405 kJ/kg
3. Answer: 400 kJ
4(a). Answer: -18.8 kJ
4(b). Answer:28.4kJ
5. Answer: 130 kJ
6. Answer: 3.96 kJ/kg
7. Answer: 70 kJ
8. Answer: -30 kJ ; 20 kJ ; 20 kJ
9. Answer: 140 kJ ; 80 kJ ; 80 kJ - 1. Each line in the following table gives information about a process of a closed system. Every entry has the same energy units. Fill in the blank spaces in the table.