2.2 - Objectives

● Introduce the forces acting on a plate moving on a fluid surface
● Describe the concept of shear strain and shear stress
● Understand the difference between the dynamic and kinematic viscosity

2.3 - Plate movement on fluid surfaces

We can start by considering a 3d rectangular element of fluid, like that in the figure below.
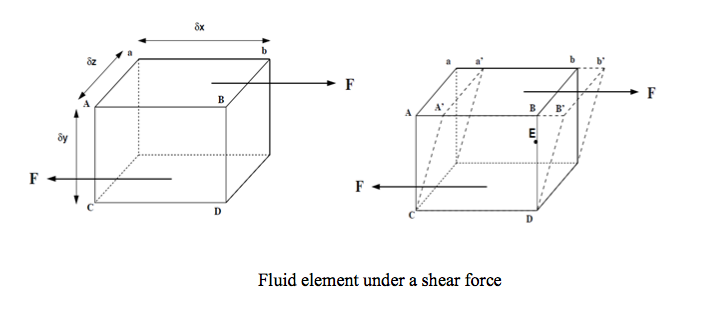
The shearing force F acts on the area on the top of the element. This area is given by A=δz X δx . We can thus calculate the shear stress which is equal to force per unit area i.e.



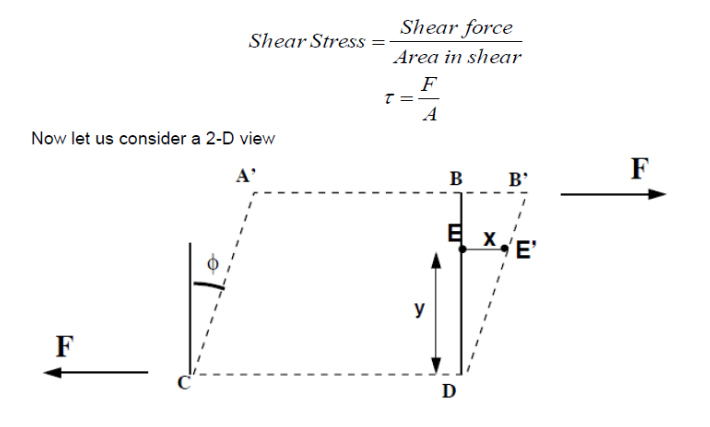
The deformation which this shear stress causes is measured by the size of the angle Ф and is known as shear strain.
It has been found experimentally that the rate of shear stress (shear stress per unit time, τ / time) is directly proportional to the shear stress.
If the particle at point E (in the above figure) moves under the shear stress to point E’ and it takes time t to get there, it has moved the distance x.
For small deformations we can write


Using the experimental result that shear stress is proportional to rate of shear strain then:


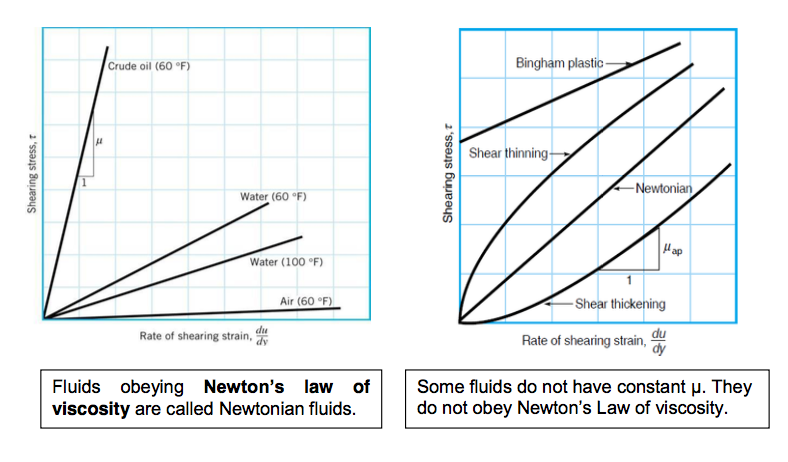
There are two ways of expressing viscosity:

Coefficient of Dynamic Viscosity:


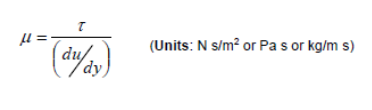
The unit Poise is also used where 10 P = 1 Pa s

Water μ = 8.94 × 10−4 N s/m2
Mercury μ = 1.526 × 10−3 N s/m2
Olive oil μ = 0.081 N s/m2
Pitch μ = 2.3 × 108 N s/m2
Honey μ = 2000 – 10000 N s/m2
Ketchup μ = 50000 – 100000 N s/m2 (non-Newtonian)


Kinematic Viscosity: The ratio of the viscosity and the density often occurs in fluid flow situation.
This ratio is called the Kinematic Viscosity (ν)

This gives a measure of the amount of viscosity per unit mass.

Water ν = 1.7 × 10−6 m2/s.
Air ν = 1.5 × 10−5 m2/s.



Example:
A thin plate of dimensions 0.4 m by 0.6 m is supported horizontally by a thin oil film of thickness 5.5 mm as shown in Figure below.
Given that the oil has a viscosity of 0.29 kg/ms, determine the force required to pull the plate at a constant velocity of 0.34 m/s, assuming a linear variation of velocity within the oil.



Example:
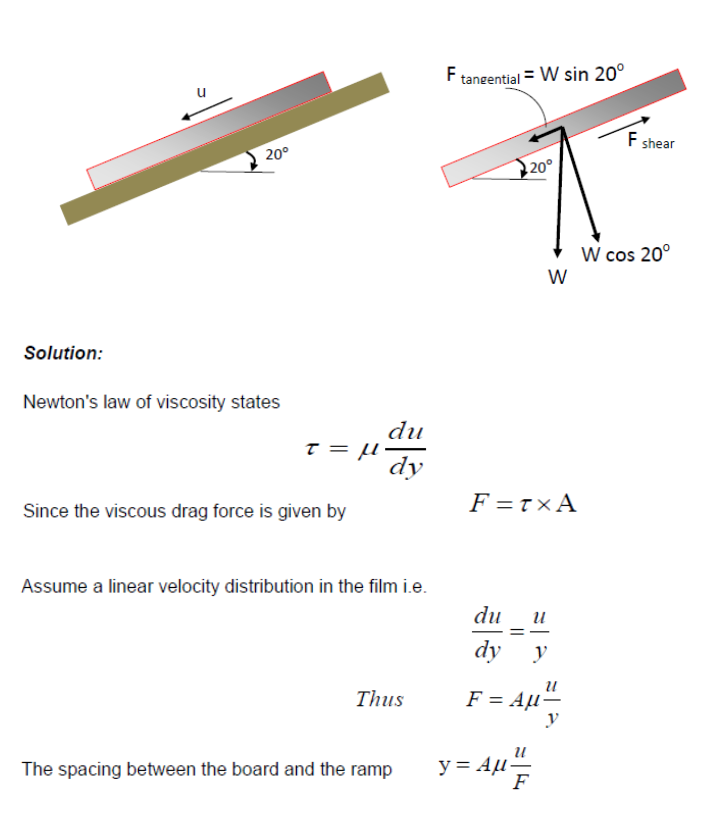
A square board (1m x 1m) that weigh 25 N slides down an inclined ramp (slope = 20o) with a velocity of 2.0 cm/s.
The board is separated from the ramp by a thin film of oil of dynamic viscosity of 0.05 Ns/m2.
Neglecting edge effects, determine the spacing between the board and the ramp

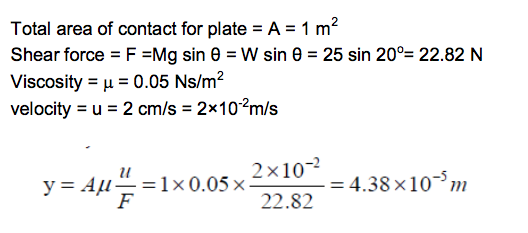
Causes of Viscosity in Fluids

Viscosity in Gases

As previously stated in a gas the molecules can move independently of each other

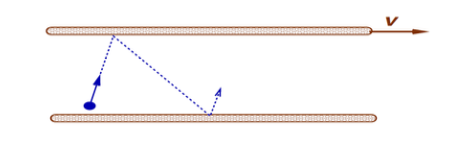
Consider the above arrangements where molecules bounce between two surfaces.
During molecule-surface collisions momentum is exchanged. Momentum interchange results in force that tends to retard relative motion. This force is called the viscosity force. Higher temperatures lead to more frequent collisions and more momentum exchange. If temperature of a gas increases the momentum exchange between layers will increase thus increasing viscosity.

Viscosity will also change with pressure - but under normal conditions this change is negligible in gasses.

Viscosity in Liquids


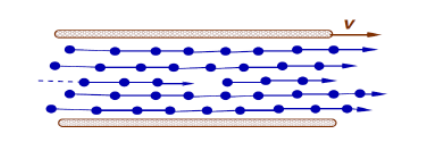
Strong intermolecular forces give the liquid its structure. Moving plate drags top layer of liquid molecules adjacent to the solid surface. The top layer of liquid molecules drags next layer, but at slower speed. And so on, layer by layer. The propagation of these forces from the top plate to the bottom plate leads to the retarding force on top plate.

Increasing the temperature of a fluid reduces the cohesive forces and increases the molecular interchange. Reducing cohesive forces reduces shear stress, while increasing molecular interchange increases shear stress. Because of this complex interrelation the effect of temperature on viscosity has something of the form:

μT = μo(1+AT + BT)

where μT is the viscosity at temperature ToC, and μo is the viscosity at temperature 0°C. A and B are constants for a particular fluid.

High pressure can also change the viscosity of a liquid. As pressure increases the relative movement of molecules requires more energy hence viscosity increases.