5.2 Objectives

● Introduce and derive the Bernoulli (energy) equation
● Demonstrate practical uses of the Bernoulli equation in the analysis of flow
● Introduce the momentum equation for a fluid
● Demonstrate how the momentum equation and principle of conservation of momentum is used to predict forces induced by flowing fluids

5.3 Bernoulli equation

The Figure below shows an element of non-viscous or ideal fluid moving along a streamline



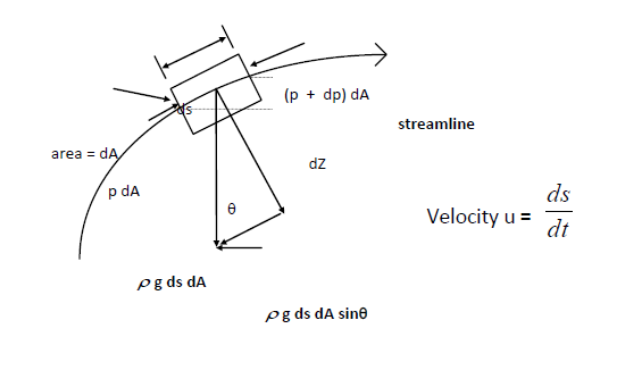
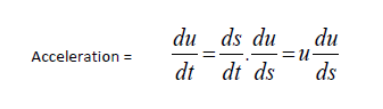
Applying Newton’s second law to the element of fluid in the s direction on a particule moving along stream line gives:

Force = mass x acceleration

In regions of flow where net frictional forces are negligible, the significant forces acting in the s direction are the pressure (acting in both sides) and the component of the weight of the particle in the s direction

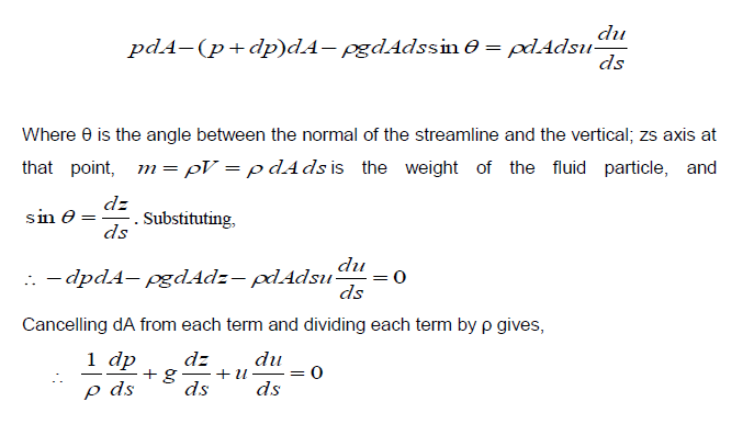
This is the Euler equation for one-dimensional incompressible flow of an ideal fluid. Integrating the equation along a streamline gives:

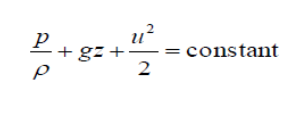
This is the famous Bernoulli equation which is commonly used in fluid mechanics for steady, incompressible flow.


The units of each term are units of energy per unit mass i.e. they are specific energy terms (J/kg).

Alternative derivation to Bernoulli equation

Consider an element of fluid moving with velocity u at a height z above a datum line.

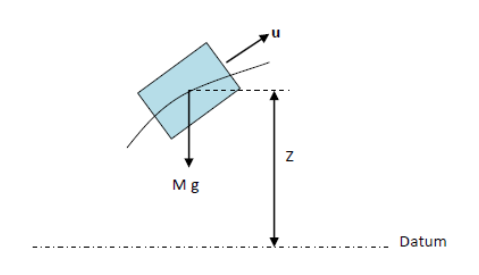
An element of fluid, as that in the figure above, has potential energy due to its height z above a datum and kinetic energy due to its velocity u. If the element has weight Mg then the those energies could be expressed as described in the followings.

5.4 Kinetic energy

Energy is required to accelerate a stationary body. Thus, a moving mass of fluid possesses more energy than an identical stationary mass. The energy difference is the Kinetic energy of the fluid

5.5 Potential Energy

Work is performed in elevating a body. Thus, a mass of fluid at a high elevation will have more energy than an identical mass of fluid at a lower elevation. The energy difference is the Potential energy of the fluid.

Potential energy = (mass)(acceleration)(height above datum)



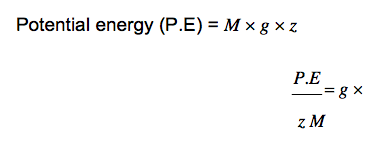
Where, z is the elevation of the fluid. The reference point (i.e. zero elevation point) is entirely arbitrary and can be chosen for convenience.

5.6 Pressure energy

Work is performed, and energy is expended, when a substance is compressed. Thus, a mass of fluid at high pressure will have more energy than an identical mass of fluid at a lower pressure. The energy difference is the pressure energy of the fluid.

The total energy possessed by the fluid per unit mass is the sum of its pressure, kinetic and potential i.e.

Total energy per unit mass = Pressure energy + Kinetic energy + Potential Energy

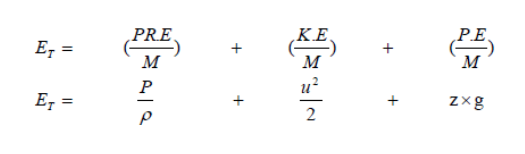
5.7 Application of the Bernoulli equation

Apply the above principles to a steady flow of incompressible fluid between points 1 and 2 in a system such as shown below:

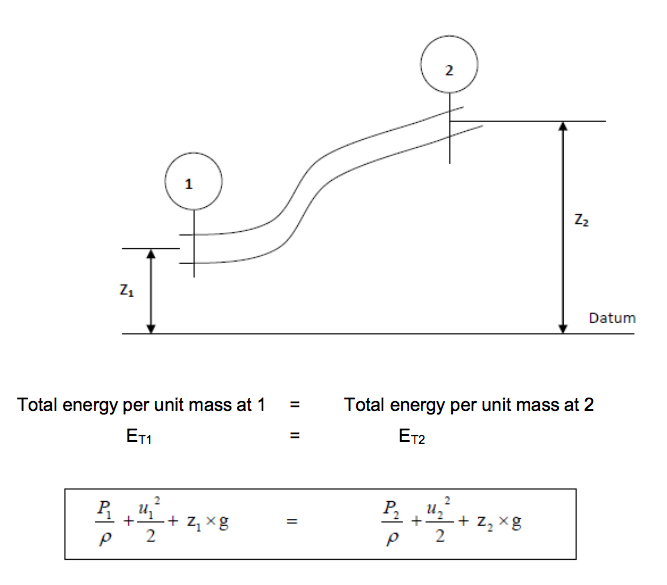
The above equation is called Bernoulli’s equation

Bernoulli’s equation is an energy conservation equation based on several reasonable assumptions. The equation assumes the following:
   ● The fluid is incompressible
   ● There is no fluid friction
   ● Changes in thermal energy is negligible

Example

The Figure below shows a steady flow of water in a 100 mm diameter horizontal pipe. The pipe has a reduced section of 50 mm in diameter forming a Venturi tube. The difference in pressure between the 100 mm and 50 mm sections is measured by a mercury filled U-tube manometer showing a reading of 445 mm. Given that the densities of water and mercury are 1000 kg m-3 and 13600 kg-3 respectively, determine:

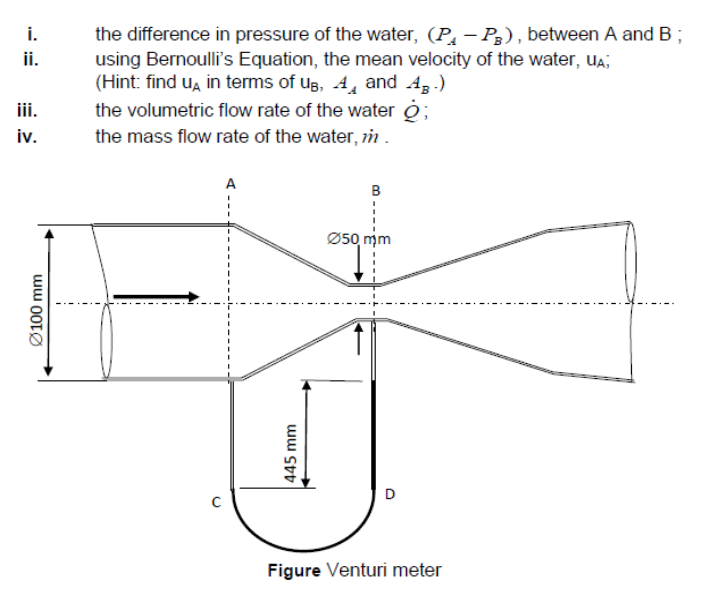
Solution  📷

Week5 Activities1-4

4 activity with randomized numbers and tasks using MapleTA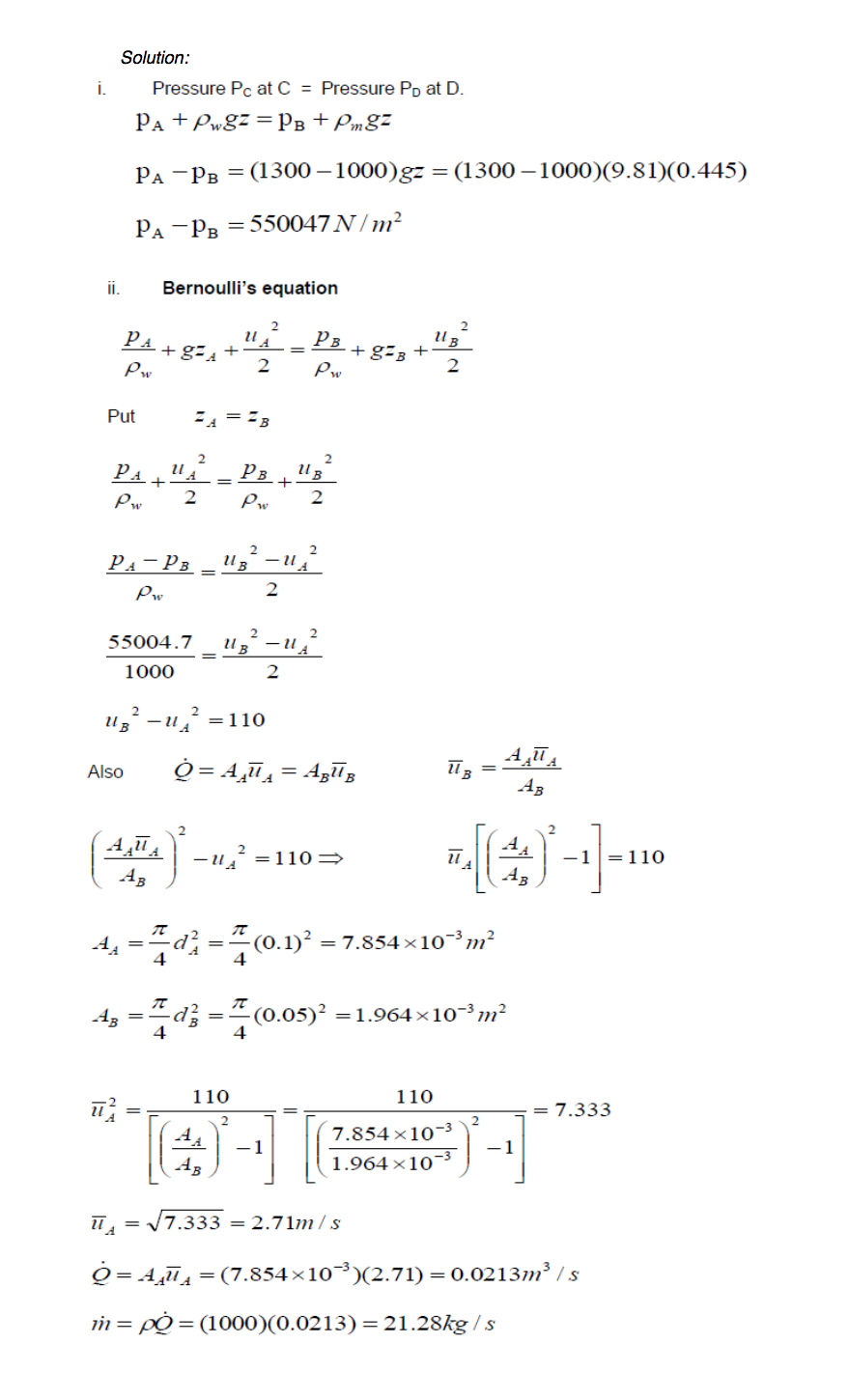

Summary

This week, we introduced and derived the Bernoulli Energy equation necessary to analyse fluids in motion.

We demonstrated the practical uses of the Bernoulli equation in the analysis of flow.

We also introduced the momentum equation for a fluid and demonstrated how the momentum equation and principle of conservation of momentum is used to predict forces induced by flowing fluids.