7.2 Changing state

It is important to remember that an object-oriented program as it runs is dynamic – objects are created as needed, and objects, once created, can change their state. If the properties of an object are encapsulated as private properties the only way to change an object’s state is to call a method of that object that makes that change.

Changing the state of an object can be so simple that it doesn’t need an algorithm. For example, a basic setter method just sets the value of the relevant field. However, some actions that result in a change of state need to implement more complex behaviour.

The example we will look at here is one you have seen before – the speedup method of the Rider class in the bicycles project. This method changes the state of the rider’s bicycle object resulting in changing its pedalRpm and gear fields. It encapsulates the rider’s knowledge of how to use the pedals and gears of the bicycle together to increase speed smoothly over the whole range of possible speeds.

To recap, the rider can only pedal at speeds up to 300rpm. Speeding up involves pedalling 50rpm faster than before. If this change would result in pedalling faster than 300rpm, then the rider should decide to tell the bicycle to change to a higher gear. At this point, the rider should adjust pedalling speed to match the current road speed – the road speed should not change immediately while changing gear.

Let’s make a first attempt at writing the algorithm to implement this knowledge. The algorithm will need to use selection as there are different possible actions depending on how fast the rider is currently pedalling.

1. if increasing pedalRpm would make it > 300
2. Change gear up and pedal slower to keep speed constant
3. else
4. Pedal 50rpm faster

Line 2 needs some thought. How do you know what value of pedalRpm is needed to keep the speed the same while changing gear? Well, if you look at the Bicycle class you see that its speed is in direct proportion to the gear. Pedalling at the same RPM in gear 2 makes the bicycle go twice as fast as in gear 1. Therefore, you would have to pedal at half the previous RPM to keep the speed the same when changing gear. Similarly, gear 3 is 3/2 times faster than gear 2 for the same RPM, so you would need to pedal at 2/3 times the previous RPM. In general, the formula for working out the new value of pedalRPM is:

new RPM = previousRPM * current gear / new gear

To implement this, you need to store the current and new gear values in variables. You need to store the current gear, then change up, then store the new gear. The algorithm can be refined to:

1. if increasing pedalRpm would make it > 300
2.1 get currentGear
2.2 Change gear up
2.3 get newGear
2.4 pedalRPM = pedalRPM * currentGear / newGear
3. else
4.1 pedalRPM = pedalRPM + 50

This refinement is detailed enough to be implemented in Java. You need to use calls to methods of the Bicycle class to find the gear and pedalRpm values and to set pedalRpm. The private method changeUp in Rider calls the changeGear method in Bicycle.

Will this always work? What if the bicycle is already in its highest gear? The algorithm that the Bicycle class uses to change gear is written so that it just stays in the same gear. So, in that case the algorithm here multiplies pedalRpm by, for example, 3/3, so pedalRpm and hence the speed stay the same.

So, here is the Java implementation that you saw earlier. It should be clear now why this is written the way it is.

public void speedUp()
{
   if((this.bicycle.getPedalRpm() + 50) > 300)
   {
       int currentGear = this.bicycle.getGear();
       changeUp();
       int newGear = this.bicycle.getGear();
       this.bicycle.setPedalRpm(
       this.bicycle.getPedalRpm() * 
       currentGear / newGear);
   }
   else
   {
       this.bicycle.setPedalRpm(
       this.bicycle.getPedalRpm() + 50);
   }
}

The Rider class has another method slowDown, which is very similar to speedUp, except that the rider pedals slower and changes gear down as required. The algorithm is slightly different. Notably, the if statement uses a compound condition. Look at this method and see if you can work out why.

You should watch the demo again from Week 5 where this method is tested and think about how the algorithm is working.

7.4 Processing information

There is often a need to take a set of input values and process these in some way to give a result, which may be a single value. An example of this would be to find the maximum value of a set of numbers. This is not quite as simple as applying a formula. The processing requires a number of steps, and you need to devise an algorithm to do this. Because there are several input values, it is likely that some processing will need to be repeated for each value, so the algorithm will probably make use of iteration.

We can write the algorithm initially using pseudocode. Pseudocode is not a real programming language – it is simply a way of thinking about and writing down what the steps for an algorithm are without worrying about the details of the actual code until we are clear about how it will work.

The algorithm for finding the maximum needs to repeatedly check numbers and keep track of the highest value found so far. We will work with a fixed sized set of numbers, so a for loop will be the best choice for iteration. Here’s a first attempt:

1. for each number in the input
2. if number greater than highest so far then this becomes highest
3. return current maximum

From thinking about the problem, it is clear that as well as iteration, this algorithm needs selection, with an if statement, as the next number may or may not be the highest so far, and we need to act differently in each case.

This is a good first attempt, but needs more thought. How do we keep track of the highest value found, how do we check and how does the highest value change? Let’s refine this algorithm to put a bit more detail in it. The numbering here helps us keep track of how the lines from the first version have been refined. The main refinement we need is to include a variable, which we will call max, to keep track of the highest value found. We can then use this variable in the condition for the if statement and set its value if the number being checked is higher.

1.1 max = 0
1.2 for each number in the input
2.1 if (number > max)
2.2 max = number
3. return max

The local variable max plays a very important role in this algorithm, a role which is common in many algorithms. Its job is to keep track of an extreme value.

This pseudocode is detailed enough to translate fairly easily into Java code. In more complex cases, more refinement steps may be needed to arrive at this point. This process is called stepwise refinement.

The final implementation of the algorithm is a method that you can find in the class NumberCruncher in the algorithms project and which is listed below. It takes a parameter that specifies the size of the set of numbers, and this is used in the initialisation of the for loop. The numbers to be processed are typed in one at a time in the terminal window as the method runs – this is done using an object input which is an instance of a class Scanner which Java provides for this purpose.

public int maximum(int listSize)
{
   int max = 0;
   for(int i=0; i<listSize; i++)
   {
       System.out.print("Next number >");
       int nextNumber = input.nextInt();
       if (nextNumber > max)
       {
           max = nextNumber;
       }
    }
    return max;
}

To try this out, create an instance of NumberCruncher in the object bench and call the method, supplying a parameter value to specify how many numbers to read in. In the terminal window, keep entering integer numbers while prompted, and the method should then return the largest one you entered.

The NumberCruncher class has another method average that calculates the average (the mean, actually) of a set of numbers. Look at the code for that method. What is the role of the local variable total? Why are the types of total and the return value double when the input values are int? Try the method out and check that it works correctly.

Processing an array

In this case the information to be processed was a list of values that need to be entered as the method runs. It is also common to need to process information that has been gathered previously and stored in, for example, an array. The NumberCruncher class has another method called maximum, with a different signature:

public int maximum(int[] numbers)
{
   int max = 0;
   for(int i=0; i<numbers.length; i++)
   {
      if (numbers[i] > max)
      {
          max = numbers[i];
      }
   }
   return max;
}

This version takes an array of integers as a parameter, and uses the length of this array to set how many times the for loop is executed. There is no need to read in values as the for loop runs as they are already stored in the array – the loop variable i is used to access each value in the array by index in turn. Apart from that, the algorithm is exactly the same as the first version of maximum.

To try this out, create an instance of NumberCruncher in the object bench and call the method, supplying an array as a parameter. You can do this easily using the shortcut technique you saw earlier for creating an array.

You have now seen some examples of methods and the algorithms they implement. Before we move on, let’s take a look in more detail about how methods are called and what happens when a method is called.

You have seen that statements are executed in the order they are written in the program, except when there are control flow statements in the code. However, some statements can call methods, for example, where b is a Bicycle object:

double currentSpeed = b.speed();
System.out.println(currentSpeed);

Here the method call is part of a sequence of statements, so the computer will appear to execute it and move on to the next statement. It may be that all you care about is the result of calling the speed method, then it makes sense to think about it this way.

Sometimes, however, you need to think in more detail about what happens as the method runs. This can be particularly important when you are trying to understand how a program works (or why it doesn’t work!).

Let’s look at this method call in more detail. Here is the call as part of a sequence of statements, and also the code for the method, in the Bicycle class. The arrows show the order in which the statements are executed.

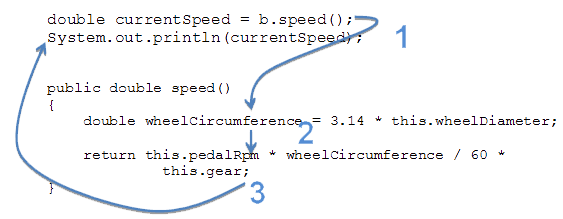
1. speed method is called, the next statement to be executed is the first statement inside the speed method
2. Statements inside the speed method are executed in sequence
3. Once the last statement in the speed method is executed, the computer returns to the calling code and executes the next statement after the method call

All method calls work like this, no matter whether the method is in the same class as the calling code or in another class.

📹 WATCH DEMO: Looking at method calls

As objects collaborate, it is common for a method to be called that in turn calls another method, which itself might call another method, and so on. Running a Java program will therefore usually involve an ever-changing chain of method calls. The computer needs to keep track of what method is currently executing, and also where it was called from in order to know where to return to when the method finishes.

The computer uses an area of its memory, known as the call stack, to do this. The name comes about because the way it works is a bit like a stack of boxes. If you stack boxes you can only get at the contents of the top box, and you need to remove the top box to get at the next one down, which then becomes the top box. In the call stack, each “box” corresponds to a method call, and is represented by a chunk of memory known as a stack frame.

The top frame corresponds to the currently executing method, and contains the parameters and local variables of that method. When that method finishes, its stack frame is removed from the stack. Execution returns to the method that made the call, whose stack frame then becomes the top frame.

Java programs start by executing the main method. As a program starts, and the code in the main method executes, main is the only method on the stack. As objects are created and methods are called, then further stack frames are added to the stack and removed when their methods finish. Once the main method finishes, its stack frame is removed and at that point the program terminates.

As an example, look at this method in the Rider class:

public void changeUp()
{
   this.bicycle.changeGear(1);
}

This method, changeUp, calls another method changeGear (in the Bicycle class – the Rider object is sending a message to its Bicycle object).

Now assume that a main method in a program has created a Rider object called myRider, and calls the changeup method:

myRider.changeUp();

The diagram below illustrates the frames on the stack as the program executes, starting on the left where the the main method frame is the only frame on the stack

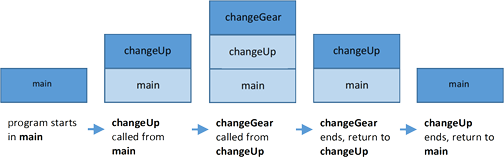
The call stack is not the only memory used to run a program. Another area of memory, called the heap, is used to store objects and their properties as the program runs. Variables of object types in the call stack can contain references to objects that are stored on the heap.