11.1 Properties of Gases

Gases have a very special part to play in thermodynamics for a number of reasons. A number of very important cyclic processes have a gas as the working fluid (Joule gas turbine cycle, Otto petrol engine cycle, Diesel engine cycle) or a condensable gas as the working fluid (Rankine steam power cycle, refrigeration cycle). The flow of gases is also clearly a major part of the study of fluid dynamics and aerodynamics. Fortunately properties of gases very often relate to one another in a very similar way.

11.2 Ideal Gases (Perfect Gases)

Gases are highly superheated vapours and under normal operating conditions they exist at temperatures well in excess of the saturation temperature. Under these conditions gases tend to obey Boyle’s law and Charles’ law.

11.2.1 Boyles Law

If a mass of gas is enclosed in a cylinder and the piston is moved up the cylinder so that the gas occupies a smaller volume then if sufficient time is allowed for any rise in temperature to subside the pressure will be seen to have increased. If we plot the volume against the absolute pressure a graph as shown will be obtained.

If we now plot the pressure against the reciprocal of the volume a straight line graph will be obtained hence we see that the pressure is inversely proportional to the volume.


This is known as BOYLES LAW viz. The absolute pressure of a given mass of gas varies inversely as its volume at its temperature remains constant. Thus for a system executing a process between two states, say state 1 and state 2, apply Boyles law gives

P1V1 = P2V2

Slide 11.1 - Boyles Law  📹

11.2.2 Charles Law

Consider now a piston enclosing a mass of gas such that the piston has a constant force applied to it, which is resisted by the pressure of the gas on the piston i.e. constant pressure. If the heat is now supplied to the gas so that the temperature increases and we plot the volume against temperature we again obtain a straight line graph which indicates that volume is proportional to temperature.


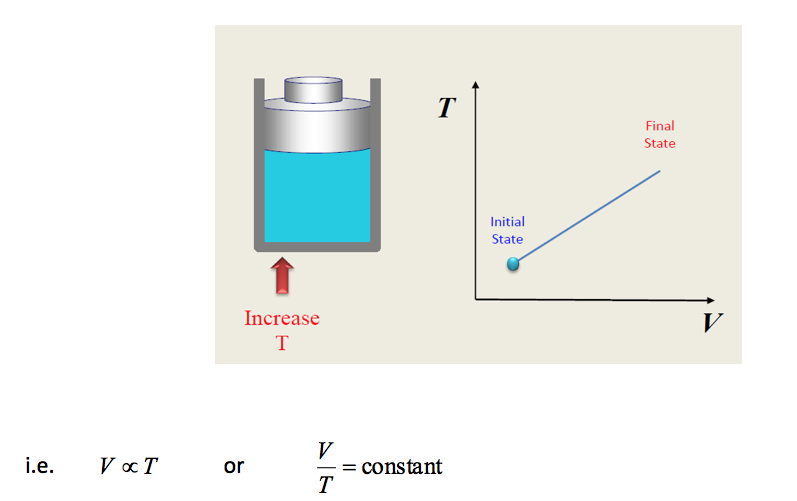
This is known as CHARLES LAW viz. For a given mass of gas at constant pressure a given increase of temperature always produces the same fractional increase in volume.

Thus for a system executing a process between two states, say state 1 and state 2, apply Charles law gives

11.2.3 Charles Law

Slide 11.2 - Charles Law  📹

If we consider now the two changes together we get:-


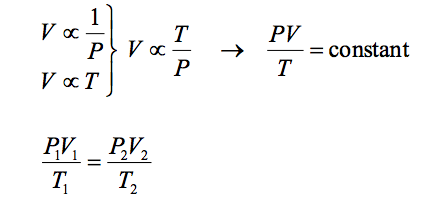
The above equation is known as the combined gas law and can be applied to ideal gases

11.2.4 Ideal Gas Equation of State

Gases at low density their molecular behaviour can be viewed as a set of randomly-moving, non-interacting molecules, except during molecular collisions. Experiments show that at normal ambient conditions such as standard temperature and pressure, most real gases behave in this manner and classed as ideal gases. Ideal gases behaviour can be approximated by:



The equation is known as the characteristic gas equation or the equation state.
If we consider AVOGADROS HYPOTHESIS which states that equal volumes of gases at the same temperature and pressure contain equal numbers of molecules then the mass contained in a particular volume will depend on the molecular mass (Mwt) of the gas.

Hence we get the relationship

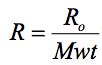
where R0 is the UNIVERSAL GAS CONSTANT and Mwt is the molecular mass of gas.

The equation would then become:

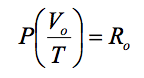
where V0 is the molar volume, ie the volume of one kilogram-mol (m3/kg. mol).

A kilogram-mol (kg.mol) is the molecular mass in kilograms

R0 and V0, are equal for all gases i.e. R0 = 8.3144kJ/kg -mol and V0 = 22.416m3/kg-mol at 0o C and standard atmospheric pressure (101.325 kN/m2).

Take the value of the gas constant for atmosphere air R = 0.287kJ/kgK

Example
The pressure in a tyre is found to be 175 kN/m2 in the morning when the temperature is 5oC. In the afternoon after a journey the temperature is found to be 25oC, determine the new pressure of the tyre assuming an increase in volume of 5%.

Solution
For change between two states apply combined gas law





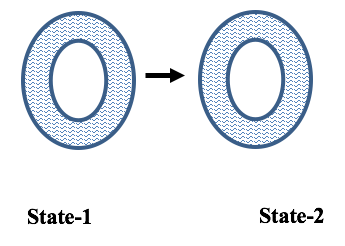
Example
A bubble of gas is emitted at a depth of 50m below the surface of a loch. Given that the volume of the bubble is 2000mm3 and the temperature is 5oC determine the volume of the bubble when it reaches the surface at a temperature of 20oC.




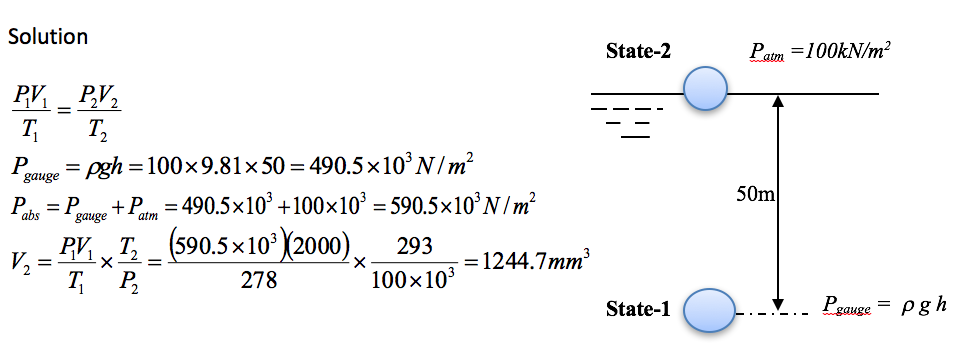
Example
Determine the specific volume of nitrogen (Mwt = 28kg/kg-mol), at a pressure of 200 kPa and a temperature of 15C.

Analysis - applying equation


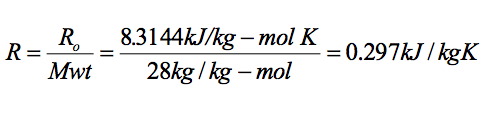
Using this value in the equation of state   PV = mRT



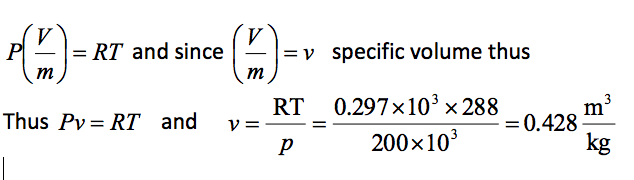
Example

A room 5m x 4m x 3m contains 72kg of air at a pressure of 101kPa. Determine the temperature of the air in the room assuming R = 0.287kJ/kg K.

Analysis - the volume of the room=V= 5 x 4 x 3 = 60m3.

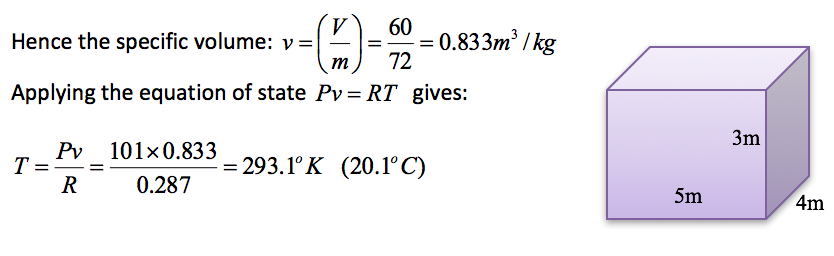
11.3 Specific Heats

Specific heats, in general, relate heat input to rise in temperature. In thermodynamics there are two definitions of specific heat relating energy terms (enthalpy and internal energy) to rise in temperature. These definitions at first site seem complex, but are usually used in an easier form depending on the simplifying assumptions that are possible.


11.3.1 Definitions of Specific Heat for Any Pure Substance

The general definitions of the specific heat terms and the symbols used are as follows:

This gives the relationship between enthalpy and temperature for a process occurring at constant pressure. Cp is not necessarily a constant.

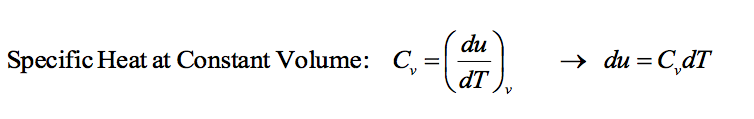
This gives the relationship between internal energy and temperature for a process occurring at constant volume. Cv is not necessarily a constant.


11.3.2 Definitions of Specific Heats for Ideal Gases

For an ideal gas obeying the ideal gas model, specific internal energy u and specific enthalpy h are both depend only on temperature T, so specific heats Cp and Cv are also function of temperature alone. This allows a simple integration of the specific heat relationships:

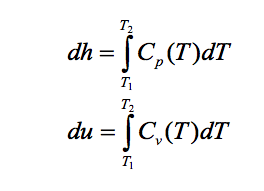
Although Cp and Cv are function of temperature but for simplicity of calculations we will assume that they are constants for ideal gases. Thus the above integrations become:



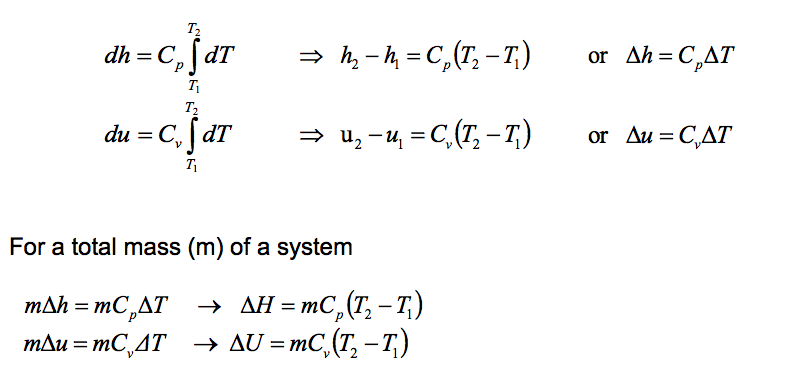
11.3.3 Ratio of Specific Heats (y)

The ratio of specific heats appears in a number of thermodynamic equations and is given the symbol

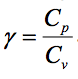
For an ideal gas, is constant.



11.3.4 Relationship between, R, Cp and Cv for an Ideal Gas (y)

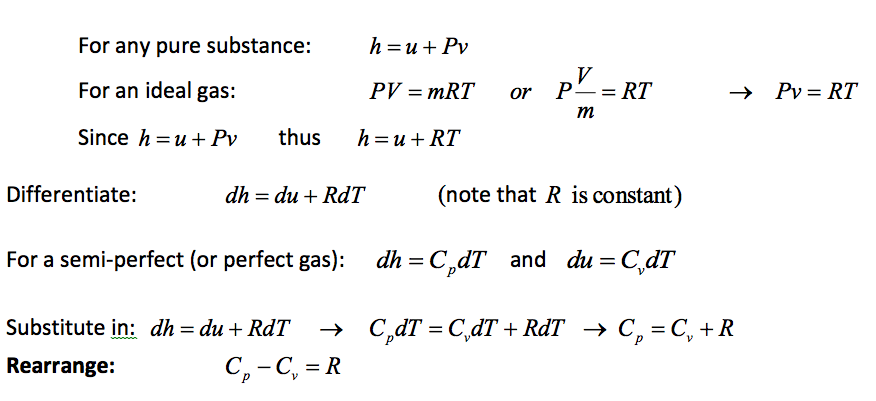
The above equation show that the specific heats of an ideal gas differ by just a constant (the gas constant, R). Knowledge of either specific heat (Cp or Cv) for a particular ideal gas allows the other to be calculated with the knowledge of the gas constant (R).

Example
When 1 kg of a perfect gas is heated from 20oC to 80oC at constant pressure, the heat input is 120 kJ. When the same gas is heated at constant volume, the heat input is 90 kJ. Find the gas constant for the perfect gas.

Thermodynamics: TUTORIAL 11: IDEAL GAS LAWS

1.	Determine the volume occupied by 0.05 kg of air at pressure of 120 KN/m2 and a temperature of 15oC. Take R (air) = 0.287 kJ/kgoK
2.	A vessel of volume 0.2 m3 contains nitrogen at 1.013 bar and 15C. If 0.2 kg of nitrogen is now pumped into the vessel, determine the new pressure when the vessel has returned to its initial temperature. The molecular weight of nitrogen is 28 kg/kg-mol and it may be assumed to be a perfect gas.
3.	0.01 kg of a certain perfect gas occupies a volume of 0.003 m3 at a pressure of 7 bar and a temperature of 131oC. Determine the molecular weight of the gas. When the gas is allowed to expand until the pressure is 1 bar the final volume is 0.02m3. Determine the final temperature.
4.	Oxygen, O2, at 200 bar is to be stored in a steel vessel at 20oC. The capacity of the vessel is 0.04 m3. Assuming that O2 is a perfect gas, determine the mass of oxygen that can be stored in the vessel. The vessel is protected against excessive pressure by a fusible plug which will melt if the temperature rises to high. Determine the temperature at which the plug must melt to limit the pressure in the vessel to 240 bar. The molecular weight of oxygen is 32 kg/ kg-mol.
5.	Determine the number of small containers that can be filled from a large air tank. Given data: R = 0.287 kg/ kg K Property      Tank      Container V (m3) 5 0.1 t (oC) 25.7 25 p (kN/m2) 600 120

Tutorial Answers  📷