12
-
- Section 12: Applications of First Law of Thermodynamics to Ideal Gases
- The aim of this section is to make use of the ideal gas relations to determine heat and work transfers and energy changes during a number of simple processes. This serves not only to demonstrate application of the First Law of thermodynamics (non-flow energy equation) but also forms the basis for future studies of the air-standard cycles including gas turbines.
Energy balance for closed system
ΔU + ΔKE + ΔPE = Q - W
Neglect kinetic and potential energy changes that the First Law reduces to
ΔU = Q - W
Below for each process we will consider the application of the non-flow processes specifically to ideal gases.
For any ideal gas the following formulae are true:
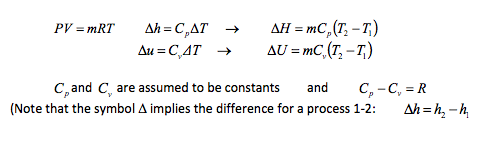
The simple nature of ideal gases formulae allows calculations of heat transfer and work for many processes to be expressed in simple terms. It also permits changes in one property to be related with little difficulty to changes in another property for which we have data.
It is most convenient to express all equations in specific terms (per kilogram of gas). To get the actual change, multiply the quantity by the mass of gas in the system. -
- 12.1 Constant-Volume Process for Ideal Gases
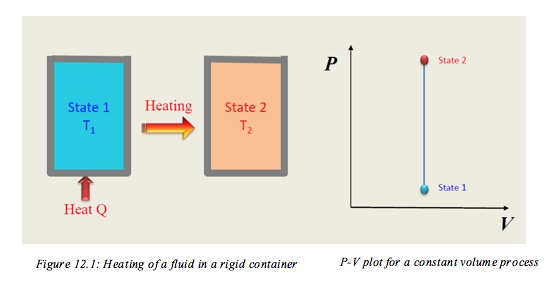
- Heating of Fluid in a rigid comtainer 📹
- Consider the process shown in Figure 12.1. If the process occurs with no change in volume, then the process is classified as a constant volume process. It is clear that during the process the volume remains constant while the pressure increases as the temperature increases.
Since there is no volume change taking place then no displacement work (PdV) then displacement work is given by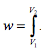 and since there is no change in volume thus dv = 0 resulting in w = 0 (note that other forms of work such as stirring may still take place).
and since there is no change in volume thus dv = 0 resulting in w = 0 (note that other forms of work such as stirring may still take place).
Now apply the first law of thermodynamics for closed system neglecting kinetic and potential energy
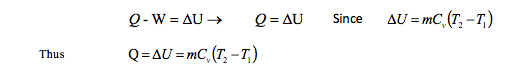
Where m is the mass, Cv is the specific heat capacity for a constant volume and T is the temperature Kelvin (K)
Also for an ideal gas, the process would be represented by.
For state 1: P1V1 = mRT1
For state 2: P2V2 = mRT2
And for the combined state: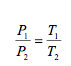
Example
A 2kg of gas, occupying 0.7 m3, had an original temperature of 15oC. It was then heated at constant volume until its temperature became 135oC. Determine the amount of heat transferred to the gas and the final pressure of the gas. Take Cv=0.72kJ / kgK and R=0.29kJ / kgK

-
- 12.2 Constant Pressure Process
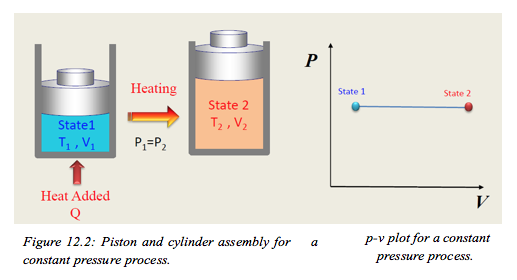
- Piston and cylinder asembly for constant pressure process 📹
It is possible to obtain a constant pressure process for a closed system using the simple construction shown in Figure 12.2. To ensure that a process is kept at a constant pressure the boundary must move as heat is added to the system. The system is normally visualised as a piston and cylinder assembly, where a mass is placed on the piston which is free to move. The mass then creates a constant force that results in a constant pressure. The constant pressure process can also be plotted on the p-v chart as shown in Figure 12.3.

Also for an ideal gas, the process would be represented by.
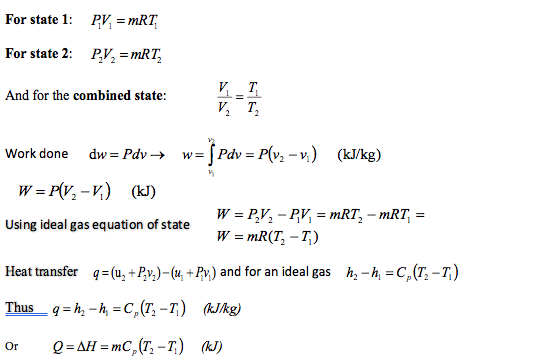
Example
A fluid inside a closed cycle undergoes a series of reversible processes. The fluid initially starts at 800kPa and specific volume of 0.05m3/kg. It is allowed to expand to a specific volume of 0.25m3/kg at a constant pressure. At this volume the pressure is then reduced to 200kPa. At this pressure the fluid is compressed until the specific volume is 0.05m3/kg. Finally, the pressure is increased to 800kPa and the fluid reaches its initial state. Determine the specific work done during this cycle.

Example
A piston cylinder device initially contains air at a pressure of 275kN/m2, volume of 0.09 m3 and a temperature of 185oC. The air is now cold at constant pressure until its temperature becomes 15oC. Determine heat transferred and the work done during this process. For air Take R = 0.29 kJ/kg K Cp = 1.005 kJ/kg K.
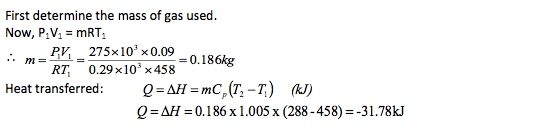
Notice the negative sign indicating that the heat has been extracted from the gas.
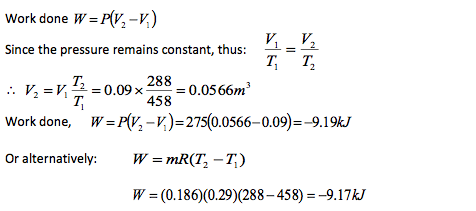
-
- 12.3 Constant Temperature / Isothermal Process
- Constant temperature Isothermal process 📹
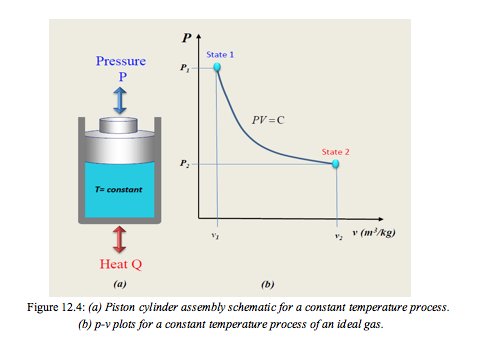
- In the derivation of Boyle’s law, the experiments conducted for any expansion or compression processes were conducted at a slow rate to ensure that any heat change in the working fluid was negligible. In normal operating conditions, however that level of control is not possible, nor desirable. It is therefore important to consider the following for a closed system;
As the pressure changes due to expansion, there is a tendency for the temperature to fall. To create an isothermal process heat must be added during the expansion as illustrated in Figure 12.4.
For compression, heat must be removed.
Constant Temperature Process for an Ideal Gas:
For an ideal gas the relationship between pressure p, volume v and temperature T is given by,
For state 1: P1V1 = mRT1
For state 2: P2V2 = mRT2
And for the combined state: P1V1 = P2V2
When T is constant a hyperbolic relationship is obtained, Figure 12.4: (b)
Since a definite constant exists it is possible to derive a relationship for the area under the p – v curve, which in turn represents the work done
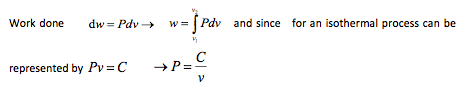

From this, then, it follows that during an isothermal expansion all the heat received is converted into external work. Conversely, during an isothermal compression, all the work done on the gas is rejected by the gas as heat. This sometimes seems a little odd at first, but if it is remembered that since the temperature must remain constant through-out, then it will be seen that the internal energy before will be the same as the internal energy after the process. Now in the case of an expansion, external work is performed by the gas. Since during an isothermal process the internal energy content of the gas must remain constant, then it appears that any heat input to the gas must immediately be dissipated in carrying out the external work. A similar analysis holds for the case of an isothermal compression. In this case the energy input is in the form of work done on the gas and this energy input is immediately rejected by the gas as heat.
Example
A piston-cylinder device contains a quantity of gas initially at a pressure of 100kPa, a temperature of 20oC and a volume of 0.3m3. The gas is now compressed in isothermal process (Pv = C) to a pressure of 500kN/m2. Determine, for this quantity of gas:
(a) the heat received or rejected (state which) during the compression,
(b) the mass of gas.
Assume for this gas that y = 1.4 and Cp = 1.0kJ/kgK
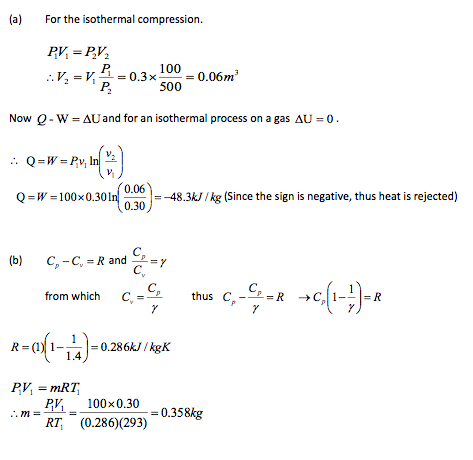
-
- 12.4 Polytropic Process
- Polytropic process video 📹
- In many real processes it is found that the status during an expansion or compression can be described approximately by a relation of the form PVn where n is a constant called the index of compression or expansion.
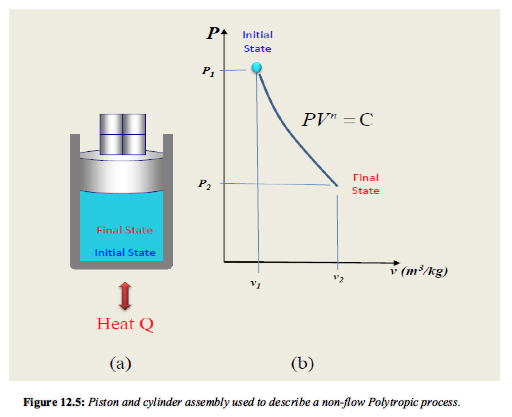
It is found that in practice many processes using both vapours and ideal gases follow the law,
PVn = Constant = C
Where n is a constant (Index of compression or expansion)
For the initial, final and any intermediate state during a reversible polytropic process
P1V1n = P2V2n = C
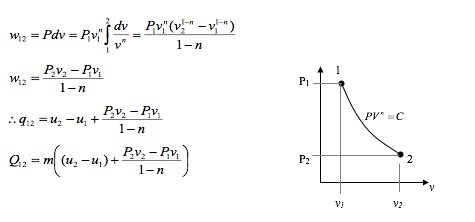
The slope of the curve representing the process on a p-v diagram increases as “n” increased.
In any polytropic process, definite quantities of heat and work cross the boundary of the system and the initial and the final states are defined by (p1) , v1) and (p2 , v2) respectively, then the index “n” can be found and hence W may be calculated.
Example
A fluid at a pressure of 200 kPa and specific volume 0.6 m3/kg is compressed within a cylinder by a piston until the specific volume is 0.2 m3/kg. If the fluid obeys the law Pv2 = constant, calculate the work done.

Note - The negative sign indicates work being done on the system.
Polytropic Process for an Ideal Gas:
A gas is no exception to this concept and so, if a mass of gas expanded or compressed, the general law of expansion or compression is of the polytropic form.
PVn = Constant = C
From the polytropic law then, if n is the polytropic index
P1V1n = P2V2n = C
Now, from equation of state:
For state 1: P1V1 = mRT1
For state 2: P2V2 = mRT2
Also, from the polytropic law.
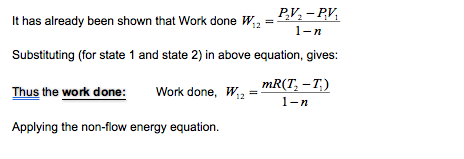
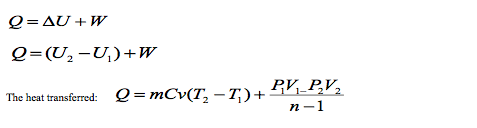
Example
0.25 kg of air at a pressure of 140 kN/m2 occupies 0.15 m3 and from this condition it is compressed to 1.4 MN/m2 according to the law PV1.25 = C.
Determine:
(a) the change of internal energy of the air,
(b) the work done on or by the air,
(c) the heat received or rejected by the air.
Take Cp = 1.005 kJ/kg K, Cv = 0.718 kJ/kgK
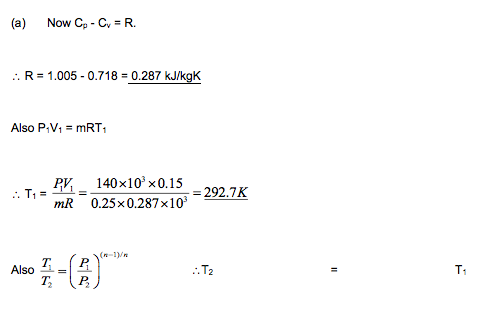

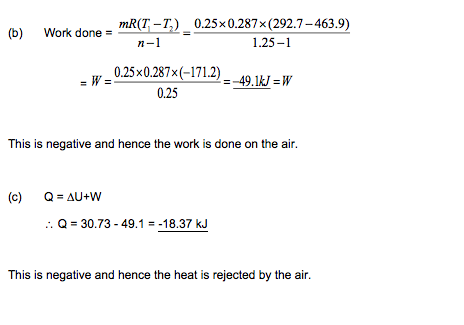
Self Assessment
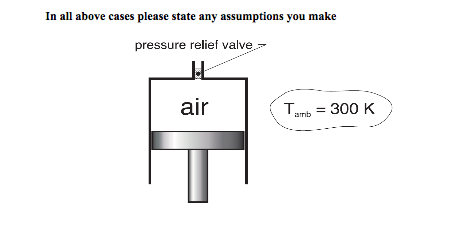
Problem T4.1: Air at 300 K, 0.14 MPa is contained in a piston-cylinder device as shown below.
The initial volume is 0.3 m3. The piston is then slowly pushed upward until the volume reaches 0.06 m3. Heat transfer with the surroundings allows the temperature of the air inside the cylinder to remain at 300 K throughout the process. The pressure relief valve at the top of the cylinder opens when the pressure reaches 0.6 MPa to allow mass to escape and thus prevent the pressure from ever exceeding 0.6MPa.
a) Determine the specific volume [m3/kg] of the air in the cylinder at the final pressure and temperature.
b) Determine the mass [kg] of the air that flows through the valve.
c) If for some reason the valve failed to open, what would the final pressure [MPa] be?
d) Determine the final temperature of the air, if the piston-cylinder is insulated (no heat transfer) and a final pressure of 0.6MPa is achieved through a reversible compressive process while the valve remains closed.
(0.1435 m3/kg; 0.0.0697kg; 07MPa; 454.9K)
-
- Thermodynamics: TUTORIAL 12: NON-FLOW PROCESSES FOR IDEAL GASES
1. A receiver of 0.85m3 capacity contains a gas at 15C and 275 kN/m2. If an additional 1.7 kg of the same gas is pumped into the receiver, what will be the pressure when the temperature is again 15oC? Calculate, also, the specific enthalpy of the gas in the initial state and final state above 0oC as the basic temperature for zero energy. Take cp = 1.005 kJ/ kg K, cv = 0.715 kJ/kg K.
2. An oxygen cylinder has a capacity of 300 litres and contains oxygen at a pressure of 3.1 MN/m2 and temperature 18oC. The stop valve is opened and some gas is used. If the pressure and temperature of the oxygen left in the cylinder falls to 1.7 MN/mo and 15oC, respectively, determine the mass of oxygen used.
If after the stop valve is closed the oxygen remaining in the cylinder gradually attains its initial temperature of 18C, determine the amount of heat transferred through the cylinder wall from the atmosphere. The density of oxygen at 0C and 0.101 325 MN/m2 may be taken as 1.429 kg/m3 and for oxygen as 1.4
3. A quantity of gas has an initial volume of 0.06 m3 and a temperature of 15oC. It is expanded to a volume of 0.12 m3 while the pressure remains constant. Determine the final temperature of the gas.
4. A mass of gas had an initial pressure of 1 bar and a temperature of 20oC. The temperature is now increased to 550oC while the volume remains constant. Determine the final pressure of the gas.
5. A certain gas has a density of 0.09 kg/m33 at 0oC and 1.013 bar. Calculate the characteristic gas constant and hence find the volume of 1 kg of this gas at 70oC and 2.07 bar. If a volume of 4.7 m3 of this gas at 1.02 bar and 0oC is heated at constant pressure to 50oC, calculate:
(a) the heat transfer:
(b) the change of internal energy:
(c) the work done.
Take cv = 10.08 kJ/kg K.
6. A certain gas has a density of 1.875 kg/m3 at 1 bar and 15oC. Calculate the characteristic gas constant R. When 0.9 kg of this gas is heated from 15oC to 250oC at constant pressure, the heat required is 175 kJ. Calculate the specific heat capacity of the gas at constant pressure and the specific heat capacity of the gas at constant volume. Calculate, also, the change of internal energy and the external work done during the heating.
7. 0.675 kg of gas at 1.4 MN/m2 and 280oC is expanded to four times the original volume according to the law pv1.3 = constant. Determine:
(i) the original and final volume of the gas
(ii) the final pressure of the gas
(iii) the final temperature of the gas
Take R = 0.287 kJ/kgK
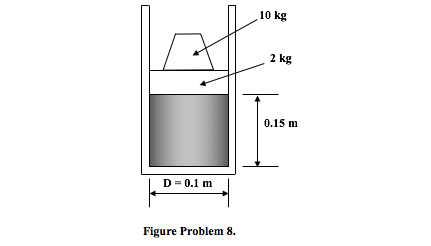
8. Consider the system shown in Figure Problem 8 in which a vertical cylinder 0.1m diameter is fitted with a frictionless, leak-proof piston of mass 2 kg which carries an additional mass of 10 kg. The atmospheric pressure is 1 bar and the air is initially at a temperature of 400o K. The air inside the cylinder is cooled and the amount of heat transfer from the system is 200 J. Assuming air to be an ideal gas and taking Rair = 0.287 kJ/kg K and Cp air=1.005kJ/kg K, determine:
i) the pressure and the mass of the air in the cylinder;
ii) the air temperature at the end of the cooling process;
iii) the downward distance moved by the piston as a result of the cooling;
iv) the work done by the air in the cylinder during the process.
- Tutorial Answers 📷
- Tutorial Answers.
1. 442 kN/m2, 15.075 kJ/kg
2. [5.5 kg, 10.725 kg
3. 303oC
4. 2.81 bar
5. 4.1229 kJ/kg K, 6.43 m3. (a) 305 kJ; (b) 215 kJ; (c) 90 kJ
6. 0.185 kJ/kgoK, 0.828 kJ/kgoK. 0.643 kJ/kgoK, 136 kJ. 39 kJ
7. (i) V1 = 0.0765 m3, V2 = 0.306 m3, (ii) P2 = 231 KN/m2; (iii) t2 = 92oC