03
-
- THE IDEAL-GAS EQUATION OF STATE
- Any equation that relates the pressure, temperature, and specific volume of a substance is called an EQUATION OF STATE. There are several equation of state. The simplest and the best known equation of state for substances in the gas phase is THE IDEAL-GAS EQUATION OF STATE.
In 1802, J. Charles and J. Gay-Lussac experimentally determined that at low pressures the volume of a gas is proportional to its temperature. That is,
P = R(\frac{T}{v})
Pv = RT
Where the constant of proportionality R is called the “GAS CONSTANT”. The above equation is called the IDEAL-GAS EQUATION OF STATE, or simply the IDEAL-GAS RELATION, and a gas that obeys this relation is called an IDEAL GAS
In this equation, P (kN/m2 or kPa/m2) is the absolute pressure, T (K) is the absolute temperature, and ν (m3) is the specific volume
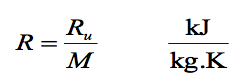
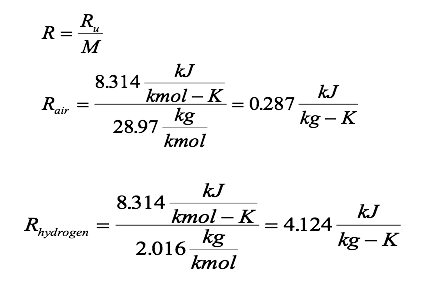
Where Ru is the UNIVERSAL GAS CONSTANT and M is the molar mass (also called molecular weight) of the gas. The constant Ru is the same for all substances, and its value is 8.314 kJ/Kmol. K or kJ/kgmol. K
The MOLAR MASS (M) can simply be defined as the “mass of one mole” (also called a gram-mole, abbreviated “gmol”) of a substance in grams, or the mass of one kmol (also called a “kilogram-mole”, abbreviated kgmol) in kilograms.
Notice that the molar mass of a substance has the way it is defined. When we say the molar mass of nitrogen is 28, it simply means the mass of 1 kmol of nitrogen is 28 kg. That is, M = 28 kg/kmol
The mass of a system is equal to the product of its molar mass M and the mole number N: m = MN (kg)
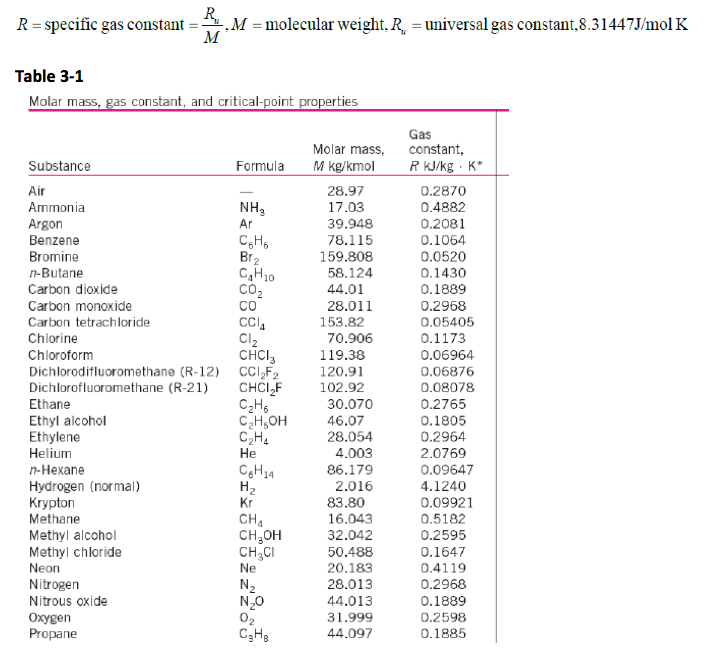
The values of R and M for several substances are given in Table below.
The ideal-gas equation of state can be written in several different forms:
V = mv → PV = mRT
Where ν is the molar specific volume, i.e., the volume per unit mole (in m3/kgmol)
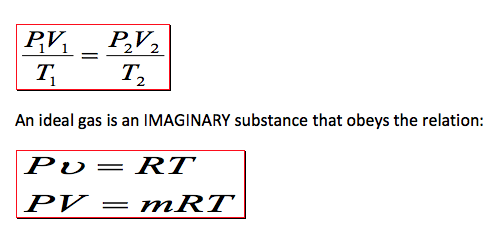
Example:
Determine the particular gas constant for air and hydrogen.
Example:
A spherical balloon with a diameter of 6 m is filled with helium at 20oC and 200 kPa. Determine the mole number and the mass of the helium in the balloon.

The volume of sphere is given by


m = MN and hence
N = \frac{m}{M} = \frac{0.03717}{4.003} = 9.285 \times 10^3 moles
Example:
A 1 m3 tank containing air at 25oC and 500 kPa is connected through a valve to another tank contain 5 kg of air at 35oC and 200kPa. Now the valve is opened, and the entire system is allowed to reach thermal equilibrium with the surroundings, which are at 20oC. Determine the volume of the second tank and the final equilibrium pressure of air.
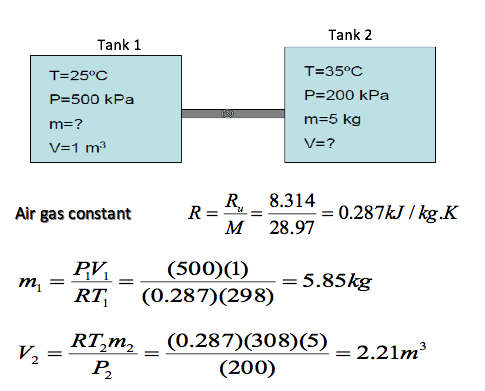
When the valve is opened, and the entire system is allowed to reach thermal equilibrium
V = V1 + V2 = 1 + 2.21 = 3.21m3
m = m1 = m2 = 5.58 = 5 = 10.85kg
T = 20 + 273 = 293K
P = \frac{mRT}{V} = \frac{(10.85)(0.287)(293)}{3.21} = 284.23kPa
IS A WATER VAPOUR AN IDEAL GAS?
The answer is yes and no.
At pressure below 10 kPA, it can be treated as one, regardless of its temperature, with errors less than 0.1 %. Thus, in air-conditioning applications, the water vapor can be treated as an ideal gas with almost no error since the vapor pressure is very low. However, in steam power plants, the pressures are usually very high – ideal-gas relations are no longer valid! -
- Useful Ideal Gas Relation: The Combined Gas Law
- By writing the ideal gas equation twice for a fixed mass and simplifying, the properties of an ideal gas at two different states are related by
m_1 = m_2 \rightarrow \frac{P_1V_1}{RT_1} = \frac{P_2V_2}{RT_2} \rightarrow \frac{P_1V_1}{T_1} = \frac{P_2V_2}{T_2}
Example:
An ideal gas having an initial temperature of 25C under goes the two processes described below. Determine the final temperature of the gas.
Process 1-2: The volume is held constant while the pressure doubles.
Process 2-3: The pressure is held constant while the volume is reduced to one-third of the original volume.

Process 1-3:
m_1 = m_1 \rightarrow \frac{P_1V_1}{T_1} = \frac{P_3V_3}{T_3}
but V3 = V1/3 and P3 = P2 = 2P1
Therefore
T_3 = T_1 \frac{P_3}{P_1} \frac{V_3}{V_1}
T_3 = T_1 \frac{2P_1}{P_1} \frac{V_1/3}{V_1} = \frac{2}{3}T_1
T_3 = \frac{2}{3}(25 + 273)K = 198.7K = -74.3 ^oC -
- Compressibility Factor, Z
- The ideal-gas relation can be used for real gases by including a correction factor called the compressibility factor Z in the ideal-gas relation, where
P_v = ZRT or Z = \frac{P_v}{RT}
Z also be written as,
Z = \frac{v_{actual}}{v_{ideal}}
where
v_{ideal} = \frac{RT}{P}
• For ideal gases, Z = 1. The farther away Z is from unity, the more the gas deviates from ideal-gas behaviour.
Normalization process: Define the following parameters
Reduced pressure, P_R = \frac{P}{P_{cr}} Reduced temperature, T_R = \frac{T}{T{cr}}
Principle of corresponding states = the Z factors for all gases is approximately the same at the same reduced pressure and temperature
By curve-fitting all data for many different type of gases, we obtain the generalized compressibility chart that can be used for all gases. These observations can be made for the chart :
• At low pressures ( PR << 1 ), gases behave as an ideal gas regardless of temperature
• At high temperatures ( TR > 2 ), ideal-gas behaviour is observed regardless of pressure (except when PR >> 1 ).
• Deviation of a gas from ideal-gas behaviour is greatest in the vicinity of the critical point
“GENERALIZED COMPRESSIBILITY CHART” is given in the figure below.
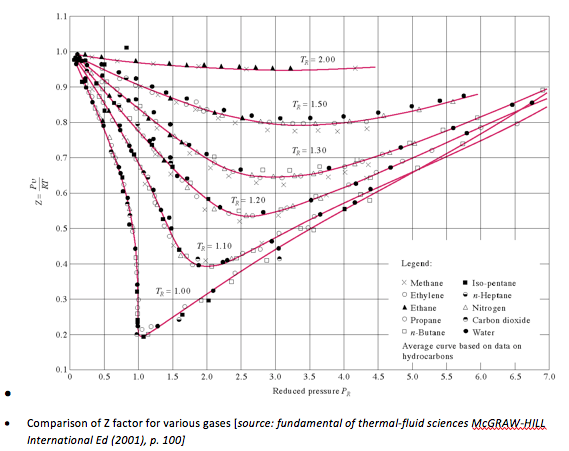
Example Determine the pressure of water vapour at 350 oC and 0.035262 m3/kg, using (a) steam tables, (b) ideal-gas relation, and (c) the generalized compressibility chart
For water vapour, R = 0.4615 kJ/kg K, Pcr = 22.06 kPa, Tcr = 647.1 K
(a) From tables, at 350 oC and 0.035262 m3/kg, → P = 7 MPa (most accurate)
(b) Using ideal-gas assumption,
P = \frac{RT}{V} = \frac{0.4615(623)}{0.035262}
= 8.15 MPa (16.4 % error)
(c) compressibility chart,
v_R = \frac{v_{actual}}{RT_{cr} | P_{cr}} = \frac{0.035262(22.064)}{0.4615(647.1)} = 2.605
T_R = \frac{T}{T_{cr}} = \frac{623}{647.1} = 0.96
From chart, PR = 0.31. Therefore, P = PR Pcr = 0.31 (22.06) = 6.84 MPa (2.3 % error) -
- OTHER EQUATIONS OF STATE.
- Many attempts have been made to keep the simplicity of the ideal gas equation of state but yet account for the intermolecular forces and volume occupied by the particles. Three of these are
Van deer Waals Equation of State
(P + \frac{a}{v^2}) (v - b) = RT
where
a = \frac{27R^2T^2_{cr}}{64P_{cr}} and b = \frac{RT_{cr}}{8P_{cr}}
Beattie-Bridgeman Equation of State
P = \frac{R_uT}{\overline v}(1 - \frac{c}{{\overline v} T^3})(\overline v + B)- \frac{A}{\overline v^2}
Where
A = A_o(1 - \frac{a}{\overline v}) and B = B_o(1 - \frac{b}{\overline v})
The constants a, b, c, Ao, Bo for various substances can be found in many references in literature.
Benedict-Webb-Rubin Equation of State
P = \frac{R-uT}{\overline v} + (B_0R_uT - A_0 - \frac{c_0}{T^2})\frac{1}{\overline v^2} + \frac{bR_uT - a}{\overline v^3} + \frac{a \alpha}{\overline v^6} + \frac{c}{\overline v^3 T^2}(1 + \frac{y}{\overline v^2})e^{-y / \overline v^2}
The constants for various substances appearing in the Benedict-Webb-Rubin equation can be found in many references in literature.
Virial Equation of State
P = \frac{RT}{v} + \frac{a(t)}{v^2} + \frac{b(t)}{v^3} + \frac{c(t)}{v^4} + \frac{d(t)}{v^5} + ... -
- Specific Heats
- Physical meaning: a thermodynamic property that characterizes the capacity of a substance to store energy
In general, this energy will depend on how the process is executed. In thermodynamics, we are interested in two kinds of specific heats:
cv = specific heat at constant volume is “the energy required to raise the temperature of a unit mass of a substance by one degree as the volume is maintained constant”.
cp = specific heat at constant pressure is “the energy required to raise the temperature of a unit mass of a substance by one degree as the pressure is maintained constant”
cp = cv because for the expansion process, work must be supplied to the system.
● c_v =(\frac{\partial u}{\partial T})_v .......... (kJ/kg.K or kJ/kg.oC)
● c_p =(\frac{\partial h}{\partial T})_p .......... (kJ/kg.K or kJ/kg.oC)
cp and cv are properties, since they are expressed in terms of other properties -
- Internal Energy, Enthalpy, and Specific Heats of Ideal Gases
- It has been demonstrated experimentally that for an ideal gas, u = u(T).
For an ideal gas, Pv = RT
Definition of enthalpy, h = u + Pv
Thus, h = u + RT
Since R is constant and u = u(T) → h = h(T)
Since u and h depend only on temperature for an ideal gas, cp and cv also depend on temperature only. Thus, for ideal gases :
c_v = (\frac{du}{dT})_y and c_p = (\frac{du}{dT})_p
Or du = cvdT and dh = cpdT
The change in internal energy or enthalpy for an ideal gas during a process from state 1 to state 2 is obtained by integrating these equations, to give:
\Delta u = u_{2} - u_{1} = \int_{1}^{2}c_vdT ...... ( kJ/kg )
\Delta h = h_{2} - h_{1} = \int_{1}^{2}c_pdT...... (kJ/kg)
Although cv and cp are temperature dependent, using average specific heats simplifies the calculations:
u_2 - u_1 = c_{v,avg}(T_2 - T_1)
h_2 - h_1 = c_{p,avg}(T_2 - T_1)
For an ideal gas, h = u + RT can be differentiated to give dh = du + RdT
Using the specific heats, c_pdT = c_vdT + RdT
Dividing by dT,
\frac{c_pdT}{dT} = \frac{c_vdT}{dT} = \frac{RdT}{dT}
gives
cp - cv = R
At this point, we introduce another ideal gas property called the SPECIFIC HEAT RATIO k, defined as
k = \frac{c_p}{c_v}
Specific Heat Characteristics
● Cp is related to enthalpy and Cv is related to internal energy and so C is a property, Unit is kJ/kg.K
● Cp and Cv are independent of processes because Cp and Cv are thermodynamic properties and Cp Cv
● Cp and Cv can be applied to any substance and any process
● Specific heats are temperature dependent
Example
Air at 300 K and 200 kPa is heated at constant pressure to 600 K. Determine the change in internal energy per unit mass using the average specific heat value (Table A-2b).
Average temperature = (300 + 900)/2 = 450 K
At this temperature from table, cv = 0.733 kJ/kg.K
Thus,
u2 - u1 = cv(T2 - T1) = 0.733 (600 – 300) = 220 kJ/kg
Example
An insulated rigid tank initially contains 0.7 kg of helium at 27 oC and 350 kPa. A paddle wheel with a power rating of 0.015 kW is operated within the tank for 30 min. Determine: (a) the final temperature and (b) the final pressure of the helium gas. Take cv as 3.1156 kJ/kg oC.
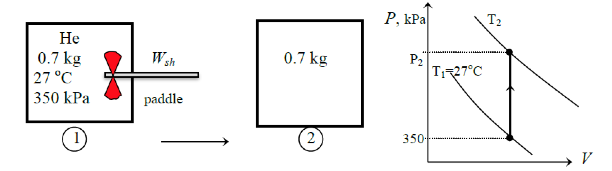
(a) The amount of paddle-wheel work done on the system is
Wsh = Wsh ∆t = 0.015 (30 x 60) = 27 kj
The system is insulated → Q = 0
Qin - Wout = m(u2 - u1) = mcv(T2 - T1)
0 - (-27) = 0.7(3.1156)(T2 - 27)→ T2 = 39.4oC
(b) At state 1,
m = \frac{P_1V}{RT_1}
and at state 2,
m = \frac{P_2V}{RT_2}
Thus
\frac{P_1}{T_1} → P_2 = T_2({P_1}{T_1}) = (39.4 + 273)(\frac{350}{27 + 273}) = 364.5 kPa
Note : In an ideal gas equation, P and T are absolute quantities ! -
- INTERNAL ENERGY, ENTHALPY, AND SPECIFIC HEATS OF SOLIDS AND LIQUIDS
- A substance whose specific volume (or density) is constant with applicable pressure is called an INCOMPRESSIBLE SUBSTANCE. The specific volume of solids and liquids essentially remain constant during a process. Therefore, liquids and solids can be approximated as incompressible substances without sacrificing much in accuracy.
Cp = Cv = C
Like those of ideal gases, the specific heats of incompressible substances depend on temperature only.
du = CvdT = C(T)dT
The change in internal energy between states 1 and 2 is then obtained by integration
\Delta u = u_2 - u_1 = \int_{1}^{2}C(T)dT \; (kJ / kg)
\Delta u = u_2 - u_1 \approx C_av(T_2 - T_1) \; (kJ / kg)
The enthalpy change of incompressible substances (solids or liquids) during process 1-2 can be determined from the definition of enthalpy (h = u + Pv) to be
h2 - h1 = (u2 - u1) + v(P2 - P1)
Since ν1 = ν2 = ν. It can also be expressed in a compact form as
∆h = ∆u + v∆P
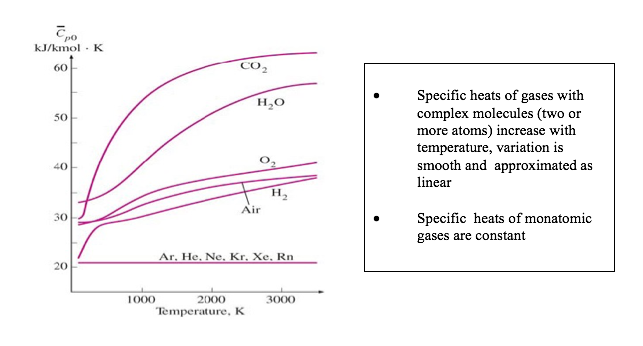
How to obtain Cv and Cp?
• Constant at room temperature ( at 300 K)

-
- Summary of Cp and Cv Application
- Constant Pressure
C-pdT - du + p dv
C_p - (\frac{\partial h}{\partial T})p
To calculate enthalpy change
dh = C_p(T)dT
\Delta h = h_2 - h_1 = \int_{1}^{2}C-p(T)dT
\cong C_{p,avg}(T_2 - T_1)- Constant volume
C-vdT = du
C_v - (\frac{\partial u}{\partial T})v
To calculate internal energy change
du = C-v(t)dT
\Delta u = u_2 - u_1 =\int_{1}^{2} C_v(T)dT)
\cong C_{v,avg}(T_2 - T_1)
- Example:
The temperature of 2 kg of neon is increased from 20oC to 180oC. Calculate the change in the total internal energy of the neon, in kJ. Would the internal energy change be any different if the neon were replaced with argon.
Since neon is a monoatomic gas and Specific heats of monatomic gases are constant, thus Cp = 21kJ/kmol. K (please see above graph)
The Molar mass of neon is M = 20.183 kg/kmol
Thus Cp = (21)/(20.183) = 1.0405 kJ/kg. K
R= 0.4119 kJ/kg. K
C_p - C_v = R \frac{kJ}{kg.K} and C_p - R = C_v
C_V = 1.0405 - 0.4119 = 0.6286kJ / kg.K
T_1 = 273 = 20 = 293K
T_2 = 273 + 180 = 453K
\Delta U = m(u_2 - u_1) = mC_v(T_2 - T_1) = 2(0.6286)(160) = 201.152kJ
Since the Molar mass of argon is different from that of molar mass of neon it is expected that the Cv to be different and hence the internal energy will be different for the condition applied.
Example:
Air at 300oK and 200kPa is heated at constant pressure to 600K. Determine the change in internal energy per unit mass, (a) using data from table A-2b, (b) the functional form of specific heat table A-2c.
(a) Using data from table A-2b
The average temperature is (300 + 600)/2= 450 K
Cv @ 450 K = 0.733 kJ/kg K
\Delta u = (u_s - u_1) = C_{v,av}(T_2 - T_1)=(0.7333)(600 - 300)= 219.9kJ / kg
(b) The functional form of specific heat table A-2c.
\overline C_p(T) = a + bT + cT^2 + dT^3
From Table A-2b: a = 28.11 b = 0.1967×10-2 c = 0.4802×10-5 d=-1.966×10-9
\overline C_p(T) = C_v(T) = R_u \frac{kJ}{kmol.K}
\overline C_v(T) = \overline C_p(T) - R_u = (a - R_u) +bT + cT^2 + dT^3
\Delta \overline U = \int_{1}^{2} \overline C_v(T)dT = \int_{1}^{2}[(a-R_u)+bT+cT^2+dT^3]dT
\Delta \overline U = [(9aT - R_uT) + \frac{1}{2}bT^2 + \frac{1}{3}cT^3 + \frac{1}{4}dT^4]_{300}^{600}
Substituting the values we obtain
\delta \overline U = 6447.15kJ / kmol
\delta U = \frac{\delta \overline U}{M} = \frac{6447.15}{28.97} = 222.5kJ / kg -
- Week 3a: Ideal Gas Tutorial
- 1. A constant mass of gas is compressed from a pressure of 1.0 bar, a volume of 0.04 m3, and a temperature of 20oC, to a pressure of 6.96 bar and a volume of 0.01 m3. Determine the final temperature of the gas.
(Ans: 509.8 K, 236.8oC)
2. A constant mass of gas is expanded from a pressure of 6.06 bar, a volume of 0.01m3, and a temperature of 171oC, to a pressure of 1.0 bar and a temperature of 20oC. Determine the final volume.
(Ans: 0.04m3)
3. Determine the mass of gas in the cylinders of Q1 and Q2 if the temperature of the gas in each case is 30oC. R for the gas is 288 J/kg⋅K. (0.045 kg; 0.069 kg) 4. A cylinder of volume 0.1 m3 contains 1 kg of air at a pressure of 20 bar. If R for air is 287 J/kg⋅K, determine the temperature of the air in the cylinder.
(Ans: 696.86 K)
5. A mass of air of 3 kg at a pressure of 400 kN/m2 and a temperature of 60oC is contained in a cylinder closed by a piston. Expansion and heat transfers cause the temperature to fall to 5oC and the pressure to 300 kN/m2. For air the gas constant may be taken as 287 J/(kg K) and the specific heat at constant volume may be taken as 718 J/(kg K).
Evaluate:
(i) the increase in the internal energy of the air,
(ii) the increase in heat energy of the air.
(Ans: -118.47 kJ, -165.83 kJ)
6. Determine the characteristic gas constant of a gas which has a specific volume of 0.5 m3/kg at a temperature of 20oC and pressure 150 kPa.
(Ans: 0.256kJ / kgK )
7. A vessel X contains gas at a pressure of 750 kPa at a temperature of 27oC. It is connected via a valve to vessel Y that is filled with a similar gas at a pressure of 1.2 MPa and a temperature of 27oC. The volume of vessel X is 2.0 m3 and that of vessel Y is 3.0 m3. Determine the final pressure at 27oC when the valve is opened and the gases are allowed to mix. Assume R for the gas to be 300 J/(kg K).
(Ans: 1020.06kPa )
-
- Reversible Non-Flow Ideal Processes
- Introduction
In Chapter 2, methods of determining the state of the working fluid were introduced. For this current section of work these previous concepts are extended and applied to specific thermodynamic processes.
A thermodynamic system is defined by the system boundary and the movement of the working fluid. If the working fluid does not cross the boundary then the system is called a closed system. If however, the working fluid crosses the boundary then the process is described as an open system.
In this Chapter we will only deal with closed systems.
Constant Volume Process
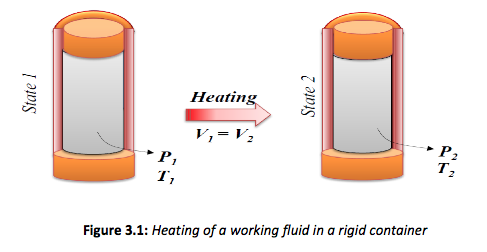
Consider the process shown in Figure 3.1. If the process occurs with no change in volume, then the process is classified as a constant volume process. It is clear that during the process the volume remains constant while the pressure increases as the temperature increases.
The consequence of this definition is that since no volumetric change has occurred then no work is done by the system. The non flow energy equation then becomes,
\varrho = \Delta U
or
q = (u_2 - u_1)
For an ideal gas, the process would be represented by Charles' law. It is also worth noting that for an ideal gas,
dw = pdv dv = 0 thus w = 0
\varrho - W = \Delta U \quad or \quad q - w = \Delta u
\varrho = |delta U \quad or \quad dq = du
c_v = (\frac{du}{dT})_v \longrightarrow dq = du = c_vdT
mdq = mdu = mn_vdT
\varrho = \Delta U = mc_v(T2 - T1)
Where m is the mass, cv is the specific heat capacity for a constant volume and T is the temperature.
Constant Pressure Process
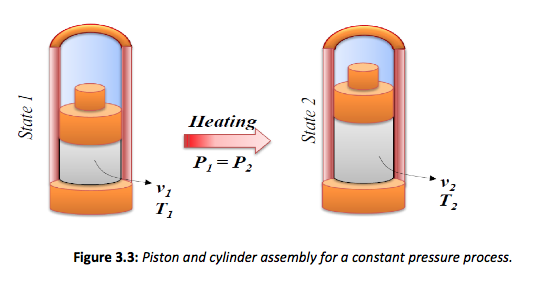
It is possible to obtain a constant pressure process for a closed system using the simple construction shown in Figure 3.3. To ensure that a process is kept at a constant pressure the boundary must move as heat is added to the system. This is similar to the experiment carried out by Charles, where the system is normally visualised as a piston and cylinder assembly, where a mass is placed on the piston which is free to move. The mass then creates a constant force that results in a constant pressure. The constant pressure process can also be plotted on the p-v chart as shown in Figure 3.4.
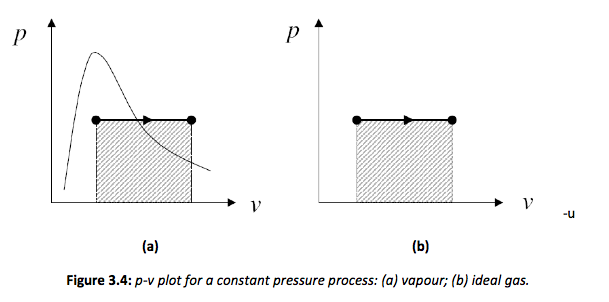
The area beneath the lines defines the work by the system. In mathematical terms the work is,
dw = pdv \quad or \quad w = \int pdv = p(v_2 - v_1)
Inserting this definition of work into the non-flow equation yields
\varrho - W = \Delta U \quad or \quad q - w = (u_2 - u_1)
q - p(v_2 - v_1) = (u_2 - u_1) or q = (u_2 + pv_2) - (u_2 + pv_1) thus q = h_2 - h_1
The latter definition arises from h = u + pv. Therefore the heat added to or subtracted from the system is a function of the change in enthalpy.
It is also worth noting that for a perfect gas,
c_p = (\frac{dh}{dT})_p \implies dh = c_pdT
mdq = mdh = mc_pdT
\varrho = \Delta H = mc_p(T_1 - T_2)
Where m is the mass, cv is the specific heat capacity for a constant volume and T is the temperature.
3.10.3 Constant Temperature/ Isothermal Process
For the experiments conducted by Boyle, any expansion or compression was conducted at a slow rate to ensure that any heat change in the working fluid was negligible. In normal operating conditions, however that level of control is not possible, nor desirable. It is therefore important to consider the following for a closed system;
• As the pressure changes due to expansion, there is a tendency for the temperature to fall. To create an isothermal process heat must be added during the expansion as illustrated in Figure 3.5.
For compression, heat must be removed.
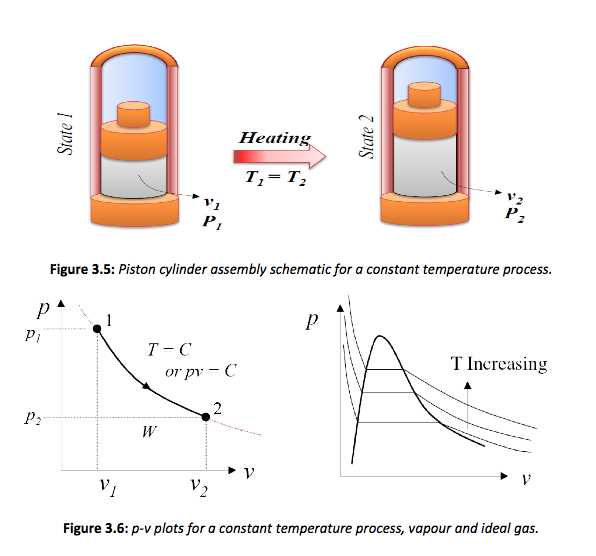
The isothermal lines on the p –v chart are illustrated above. Note that both the temperature and pressure remain constant in the wet vapour range. In the liquid and super heated range the temperatures changes relative to the pressure. Each of these isothermal lines defines an isothermal process. This process is easily defined in the wet vapour range, but is more difficult in the superheated range. The heat supplied in the wet vapour range is simply h2 – h1, the internal energy is u2 – u1, therefore the work is F
w = q - (u_2 - U_1) \quad or \quad w = (h_2 - h_1) - (u_2 - u_1)
or an ideal gas the relationship between pressure p, volume v and temperature T is given by,
pv = RT \quad or \quad pV = mRT
When T is a constant a hyperbolic relationship is obtained,
pv = constant = c
Since a definite constant exists it is possible to derive a relationship for the area under the p – v curve,
w=\int_{v_1}^{v_2}pdv \quad or \quad w=\int_{v_1}^{v_2}\frac{c}{v}dv
w=cln(\frac{v_1}{v_2})
Since p1v1 = constant = p2v2 then we can also write,
w=p_1v_1ln(\frac{v_1}{v_2}) \quad or \quad w=p_2v_2ln(\frac{v_1}{v_2})
likewise
w=p_1v_1ln({p_2}{p_1})
Several other formulations exist each of which can be derived from first principals. The final form of the equation will depend on the process. It is also worth noting that from joules law for a constant temperature process,
\Delta U = (U_2 - U_1) = mc_v (T_2 - T_1) = 0
(U_2 - U_1) = 0
Therefore for an ideal gas ONLY \varrho - W = 0
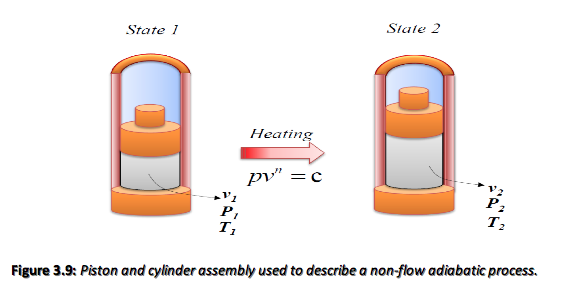
3.10.4 Adiabatic Processes
An adiabatic process is one in which no heat transfer occurs, i.e. the systems is perfectly insulated, therefore q = 0. The non-flow energy equation then becomes,
-w = u_2 - u_1
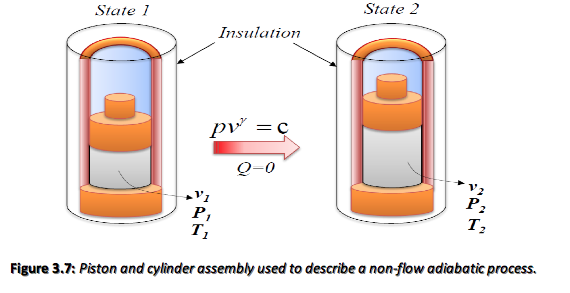
For the non-flow expansion shown in Figure 3.7, the temperature drops as the piston moves upwards. It is possible to derive a relationship between p and v for a perfect gas,
pv^\gamma = constant = c
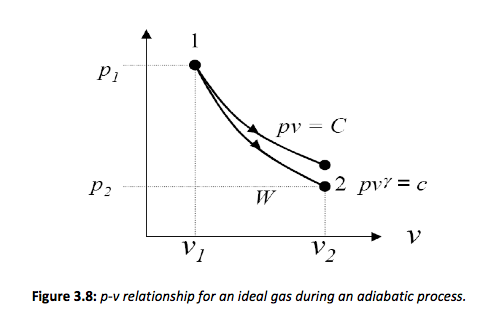
Each ideal gas will have a unique value of \gamma(\gamma = cp / cv). The process can also be represented graphically as illustrated in Figure 3.8. Note that for an ideal gas the temperature changes during the process, for the expansion shown in Figure 3.7 the temperature drops.
The work can therefore be defined as,
w=\int_{v_1}^{v_2}pdv \quad or \quad w=\int_{v_1}^{v_2}\frac{c}{v^\gamma}dv
w=c \left [\frac{v^{-\gamma+1}}{-\gamma + 1}\right]^{v_2}_{v_1} = c \left[ \frac{v_2^{1-\gamma}-v_1^{1-\gamma}}{1-\gamma} \right]=\left [ \frac{p_2v_2^\gamma v_2^{1-\gamma} - p_1v_1^\gamma v_2^{1-\gamma}}{1-\gamma} \right]
w=\left [ \frac{p_2v_2-p_1v_1}{1-\gamma} \right ]
Each ideal gas will have a unique value of γ (γ= cp/cv). This value can also be represented graphically as,
3.10.5 Ploytropic Processes
It is found that in practice many processes using both vapours and ideal gases follow the law,
pv^n = constant = c
Where n is a constant. Following the same integration method as used above for the adiabatic process the work can be defined as,
w=\left [ \frac{p_2v_2-p_1v_1}{1-n} \right ]
Using the same methods illustrated for the isothermal process it is possible to derive further equations using Pν = RT, detailed derivations can be found elsewhere. One useful relationship that can be applied to ideal gases is,
q=\left [ \frac{n=y}{1-y} \right ]w
Then by assuming different values of n,
n = 0, pv0 = constant, p = constant, Constant Pressure Process.
n = 1, pv1 = constant, pv = constant, Isothermal Process.
n = g, pvγ = constant, Adiabatic Process.
n = ∞, pv∞ = constant, v = constant, Constant volume Process.
All of these functions can only be applied to an ideal gas.
-
- Self Assessment (3-1): Non-flow processes for gases:
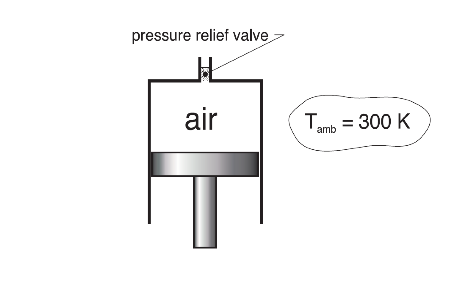
- Air at 300 K, 0.14 MPa is contained in a piston-cylinder device as shown below. The initial volume is 0.3 m3. The piston is then slowly pushed upward until the volume reaches 0.06 m3. Heat transfer with the surroundings allows the temperature of the air inside the cylinder to remain at 300 K throughout the process. The pressure relief valve at the top of the cylinder opens when the pressure reaches 0.6 MPa to allow mass to escape and thus prevent the pressure from ever exceeding 0.6MPa. For air take Cp=1.005kJ/kgK and Cv=0.718 kJ/kgK.
a) Determine the specific volume [m3/kg] of the air in the cylinder at the final pressure and temperature.
b) Determine the mass [kg] of the air that flows through the valve.
c) If for some reason the valve failed to open, what would the final pressure [MPa] be?
d) Determine the final temperature of the air, if the piston-cylinder is insulated (no heat transfer) and a final pressure of 0.6MPa is achieved through a reversible compressive process while the valve remains closed.
(0.1435 m3/kg; 0.0.07kg; 0.7MPa; 454.67K)
-
- Week 3b: Non-flow Processes for Gases: Tutorial
- 1. A constant mass of gas is expanded at a constant temperature from a pressure of 10 bar and a volume of 0.15 m3 to a volume of 0.2 m3. Determine the final pressure.
(7.5 bar)
2. A cylinder 0.04 m3 in volume contains gas at a pressure of 1.0 bar. Given that the gas is compressed according to the law pV1.4 = C until the volume is 0.01 m3, determine the final pressure.
(6.96 bar)
3. If the gas has the same initial conditions as in Q2 is compressed according to the law pV1.3 = C. Given that the final volume is 0.01 m3, determine the final pressure.
(6.06 bar)
4. Give an expression for the relationship between the mass m, pressure p, volume V and temperature T for an ideal gas. Indicate clearly the units in which each of these properties is measured for the expression to be consistent. A mass of 50 g of an ideal gas is initially at ambient temperature 17 oC and pressure 1.0 bar. In two separate experiments it is compressed in a cylinder to a pressure 4000kPa under different conditions: (a) With the cylinder fully insulated, (b) Slowly and with no insulation of the cylinder. Determine in each case the final gas temperature and the initial and final volumes. Take ɤ=1.3 and R = 190 J/kg K
[(a): 408.72 oC, 0.0276 m3 0.0016 m3) (b): 17 oC 0.0276 m3 0.0016m3]
5. At the start if expansion in an engine cylinder the burnt gases are at a temperature of 650 oC and pressure 3.2 MN/m2. The gases expand to ten times their original volume before being exhausted from the cylinder. Calculate the pressure and temperature of the exhausted gases, assuming the expansion to take place according to the law pV1.25 = constant.
(180 kN/m2; 246 oC)
6. A motor cycle engine has an 11 to 1 compression ratio, i.e. the ratio of initial to final volume during compression is 11 to 1. If the inlet pressure and temperature are 96kN/m2 and 37 oC respectively, calculate the final pressure and temperature. Assume compression according to the law pV 1.32 = constant.
(2.27 MN/m2; 394 oC) -
- Week 3c: Non-flow Processes for Steam: Tutorial
- 1. A well-insulated rigid tank contains 5 kg of a saturated liquid–vapour mixture of water at l00 kPa. Initially, three-quarters of the mass is in the liquid phase. An electric resistor placed in the tank is connected to a 110 V source and a current of 8 A flows through the resistor when the switch is turned on. Determine how long it will take to vaporize all the liquid in the tank. Also, show the process on a T-v diagram with respect to saturation lines.
(153.2 min)
2 An insulated piston–cylinder device contains 5 L of saturated liquid water at a constant pressure of 175 kPa. Water is stirred by a paddle wheel while a current of 8 A flows for 45 min through a resistor placed in the water. If one-half of the liquid is evaporated during this constant-pressure process and the paddle-wheel work amounts to 400 kJ, determine the voltage of the source. Also, show the process on a P-v diagram with respect to saturation lines.
(223.9V)
3 A piston-cylinder device contains a saturated liquid-vapour mixture of water at 800kPa pressure. The mixture is heated at constant pressure until the temperature rises to 350°C. Draw the process on a P-V diagram and determine: a. The initial temperature;
b. the total mass of water;
c. the final volume.
(170.41oC; 93.45Kg; 33.12 m3)
4 A piston-cylinder device is initially filled with water at 40 oC and 200kPa. The device is heated at constant pressure until all the liquid has vaporized. Draw the process on a T-V diagram and determine: a. the mass of water;
b. the final temperature;
c. the total enthalpy change.
(49.61kg; 120.21oC; 125,943 kJ)
5. A rigid vessel that contains a saturated liquid-vapour mixture at 150oC is heated until it reaches the critical state. Determine:
a) The mass of the liquid water;
b) the volume occupied by the liquid at the initial state.
(96.60kg; 0.105m3)
6. Saturated water vapour in a cylinder at 300 kPa is heated at constant pressure until its temperature rises to 200oC. Determine the boundary work done during this process.
(165.9kJ) -
- right