05
-
The Second Law of Thermodynamics
- Introduce the second law of thermodynamics which asserts that processes occur in a certain direction and that energy has quality as well as quantity.
- A process cannot take place unless it satisfies both the first and second laws of thermodynamics.
- The thermal energy reservoirs, reversible and irreversible processes, heat engines, refrigerators, and heat pumps are introduced.
- The Carnot cycle is introduced, and the Carnot principles are examined.
5.1 Introduction to the Second Law of Thermodynamics
- As pointed out repeatedly in the preceding chapters, energy is conserved property, and no process is known to have taken place in violation of the first law of thermodynamics. Therefore, it is reasonable to conclude that a process must satisfy the first law to occur. However, as explained below, satisfying the first law alone does not ensure that the process will actually take place.
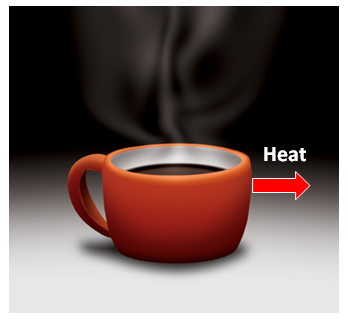
- A cup of hot coffee does not get hotter in a cooler room
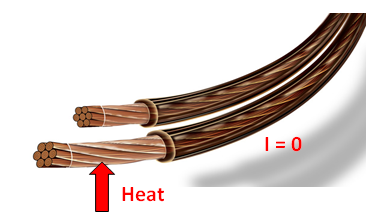
- Transferring heat to a wire will not generated electricity
- It is clear from the above that processes proceed in a certain direction and not in the reverse direction.

- The first law places no restriction on the direction of a process, but satisfying the first law does not ensure that the process will actually occur. This inadequacy of the first law to identify whether a process can take place is remedied by introducing another general principle, THE SECOND LAW OF THERMODYNAMICS.
- We show later in this chapter that the reverse process discussed above violate the second law of thermodynamics. This violation is easily detected with the help of a property, called ENTROPY. A process will not occur unless it satisfies both the first and the second laws of thermodynamics.
-
5.2 Thermal Energy Reservoirs
- Thermal energy reservoir (or reservoir) = a body that can supply or absorb finite amounts of heat without undergoing any change in temperature.
- Examples:
- Large bodies of water – oceans, lakes and rivers because they have large thermal energy capacity (mass x specific heat)
- Atmospheric air because of its large mass
- A two-phase system because it can absorb and release large quantities of heat while remaining at constant temperature
- Industrial furnace, since it operates isothermally where its temperature is controlled.
- Any physical body with large thermal energy capacity relative to the amount of energy it supplies or absorbs can be modeled as a reservoir. The air inside a large room can be considered a reservoir when it absorbs heat from a TV set, because the amount of heat transfer is not large enough to noticeably change the air temperature.
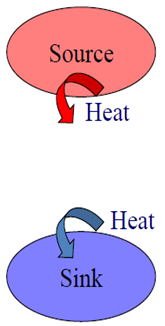
- source = a reservoir that supplies energy in the form of heat
- sink = a reservoir that absorbs energy in the form of heat
- Thermal energy reservoirs are also known as heat reservoirs.
-
5.3 Heat Engines
- The work can easily be converted to other forms of energy, but converting other forms of energy to work is not that easy.
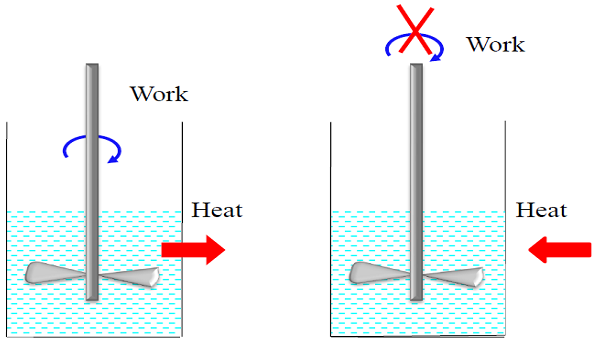
- From this and other observations, we conclude that work can be converted to heat directly and completely, but converting heat to work requires the use of some special devices. These devices are called HEAT ENGINES.
- Heat engines differ considerably from one another, but all can be characterized by the following:
- 1. They receive heat from a high-temperature source (solar energy, oil furnace, nuclear reactor, etc.).
- 2. They convert part of this heat to work (usually in the form of a rotating shaft).
- 3. They reject remaining waste heat to a low-temperature sink (the atmosphere, rivers, etc.)
- 4. They operate on a cycle.
- Heat engines and other cyclic devices usually involve a working fluid to and from which heat is transferred while undergoing a cycle. Working fluid = a fluid in heat engines (and other cyclic devices) to and from which heat is transferred while undergoing a cycle.
- A steam power plant, which is an external combustion engine, is a good example of a heat engine The term HEAT ENGINE is often used in a broader sense to include work-producing devices that do not operate in a thermodynamic cycle.

- Note: water is the working fluid in a steam power plant!
- It is sufficient to draw a simplified diagram of a heat engine as follows
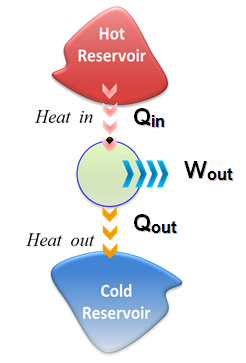
- Part of the heat received by a heat engine is converted to work, while the rest is rejected to a sink
- This is a rather simplified diagram. The various quantities shown on this figure are as follows:
- Qin: amount of heat supplied to steam in boiler from a high-temperature source (furnace).
- Qout: amount of heat rejected from steam in condenser to a low-temperature sink (the atmosphere, a river, etc.).
- Wout: amount of work delivered by a steam as it expands in turbine.
- Win: amount of work required to compress water to boiler pressure.
- Notice that the directions of the heat and work interactions are indicated by the subscripts in and out. Therefore, all four quantities described above are always positive.
- The net work output of this power plant is simply the difference between the total work output of the plant and the total work input.
- W_{net} = W_{out} - W_{in} \qquad \qquad \textrm{(kJ/kg)........5-1}
- The power plant analyzed as a closed system undergoing a cycle, the change in internal energy \Delta \cup = 0 , and therefore the net work output of the system is also equal to the net heat transfer to the system:
- W_{net} = Q_{out} - Q_{in} \qquad \qquad \textrm{(kJ/kg)........5-2}
Thermal Efficiency:
- In the equation 5-2, Qout represents the magnitude of the energy wasted in order to complete the cycle. But Qout is never zero; the net work output of a heat engine is always less than the amount of the heat input. That is, only part of the heat transferred to the heat engine is converted to work. The fraction of the heat input that is converted to the net work output is a measure of the performance of a heat engine and is called the THERMAL EFFICIENCY \left ( \eta_{th} \right)
- Performance or efficiency, in general, can be expressed in terms of the desired output and the required input as
- \text{performance}= \frac{\text{desired output}}{\text{desired input}}
- For heat engines, the desired output is the net work output, and the required input is the amount of the heat supplied to the working fluid. Then the thermal efficiency of the heat engine can be expressed as:
- \text{Thermal efficiency}= \frac{\text{net work output}}{\text{total heat input}}
- Or \eta_{th} = \frac{W_{net}}{Q_{in}}
- It can also be expressed as: \eta_{th} = 1 - \frac{Q_{out}}{Q_{in}}
- Cyclic devices of practical interest such as heat engines, refrigerators, and heat pumps operate between a high-temperature medium (or reservoir) at temperature TH and low-temperature medium (or reservoir) at temperature TL. To bring uniformity to the treatment of heat engines, refrigerators, and heat pumps, we define the following two quantities:
- QH: magnitude of the heat transfer between cyclic device and high-temperature medium at temperature TH.
- QL: magnitude of heat transfer between cyclic device and low-temperature medium at temperature TL.
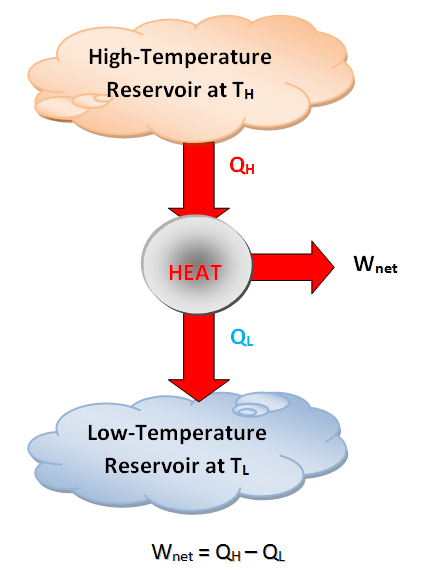
- \eta_{th}=\frac{W_{net}}{Q_H} \qquad \qquad \eta_{th}=1
- If QH = 100 MJ, Wnet = 40 MJ and QL = 60 MJ
- \eta_{th} = 1 - \frac{60 MJ}{100 MJ} = 0.4 \textrm{(or 40\%)}
- Example 5-1A steam power plant produces 50 MW of net work while burning fuel to produce 150 MW of heat energy at the high temperature. Determine the cycle thermal efficiency and the heat rejected by the cycle to the surroundings.
- W_{net, out} = Q_H - Q_L
- Q_L = Q_H - W_{net,out}
- = 150 MW - 50 MW
- = 100 MW
- \eta_{th} = \frac{W_{net, out}}{Q_H}
- = \frac{50 MW}{150 MW} = 0.333 \qquad \textrm{or} \qquad 33.3\%
- Can We Save Qout?
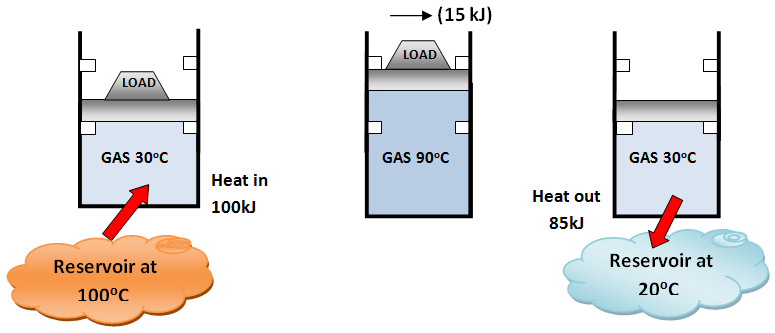
- A heat engine cycle can not be completed without rejecting some heat to the low temperature sink
- THE SECOND LAW OF THERMODYNAMICS: Kelvin-Plank Statement
- “It is impossible for any device that operates on a cycle to receive heat from a simple reservoir and produce a net amount of work”
- The Kelvin-Plank statement can also be expressed as follows: “No heat engine can have a thermal efficiency of 100 percent, or for a power plant to operate, the working fluid must exchange heat with environment as well as furnace”.

-
5.4 The Carnot Cycle
- Reversible cycles cannot be achieved in practice because the irreversibilities associated with each process cannot be eliminated. However reversible cycles provide upper limits on the performance of real cycles.
- Heat engines and refrigerators that work on reversible cycles serve as models to which actual heat engines and refrigerators can be compared.
- Reversible cycles also serve as starting points in the development of actual cycles and are modified as needed to meet certain requirements.
- Probably the best known reversible cycle is the CARNOT CYCLE, first proposed in 1824 by a French engineer Sadi Carnot. The theoretical heat engine that operates on the Carnot cycle is called the CARNOT HEAT ENGINE.
- The Carnot cycle is composed of four reversible processes-two isothermal and two adiabatic- and it can be executed either in a closed or a steady-flow system.
- Consider a closed system that consists of gas contained in an adiabatic piston-cylinder device. The four reversible processes that make up the Carnot cycle are as follows:
- REVERSIBLE ISOTHERMAL EXPANSION.- (Process 1-2, TH=constant). Initially the temperature of the gas is TH, and the cylinder head is in closed contact with a source a temperature TH. The gas is allowed to expand slowly, doing work on the surroundings. The amount of total heat transferred to the gas during this process is QH.
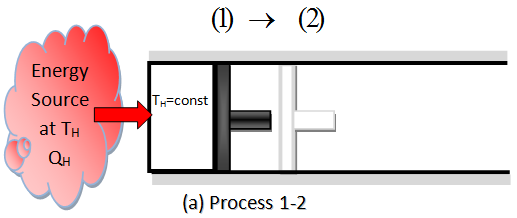
- REVERSIBLE ADIABATIC EXPANSION.- (Process 2-3, temperature drops from TH to TL). At state 2, the reservoir that was in contact with the cylinder head is removed and replaced by insulation so that the system becomes adiabatic. The gas continues to expand slowly, doing work on the surroundings until its temperature drops from TH to TL (step 3). The piston is assumed to be frictionless and the process to be quasi-equilibrium, so the process is reversible as well as adiabatic.

- REVERSIBLE ISOTHERMAL COMPRESSION.- (Process 3-4, TL= constant). At state 3, the insulation at the cilynder head is removed, and the cylinder is brought into contact with a sink at temperature TL. Now the piston is pushed inward by an external force, doing work on the gas. As the gas is compressed, its temperature tends to rise. But as soon as it rises by an infinitesimal amount dT, heat flows from the gas to the sink, causing the gas temperature to drop to TL. The amount of heat rejected from the gas during this process is QL.

- REVERSIBLE ADIABATIC COMPRESSION.- (Process 4-1, temperature rises from TL to TH). State 4, is such that when the low-tmeperature reservoir is removed and the insulationis put back on the cylinder head and the gas is compressed in a reversible manner, the gas returns to its initial state (state 1). The temperature rises from TL to TH during this reversible adiabatic compression process, which completes the cycle.

- Execution of the carnot cycle in a closed system
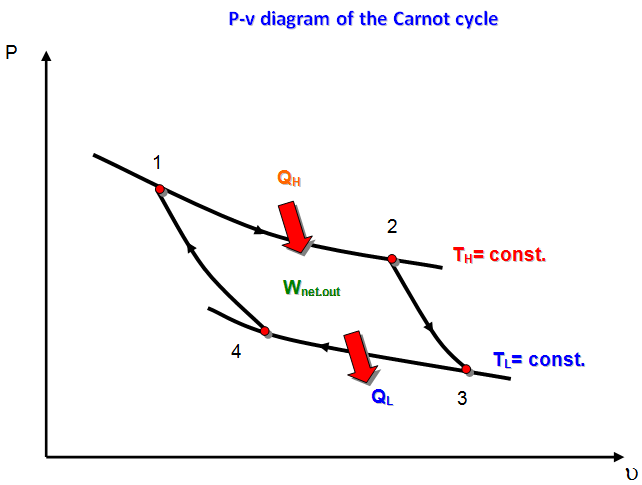
The Carnot Cycle
- Process 1-2:Reversible isothermal heat addition at high temperature, TH > TL, to the working fluid in a piston-cylinder device that does some boundary work.
- Process 2-3:Reversible adiabatic expansion during which the system does work as the working fluid temperature decreases from TH to TL.
- Process 3-4:The system is brought in contact with a heat reservoir at TL < TH and a reversible isothermal heat exchange takes place while work of compression is done on the system.
- Process 4-1:A reversible adiabatic compression process increases the working fluid temperature from TL to TH
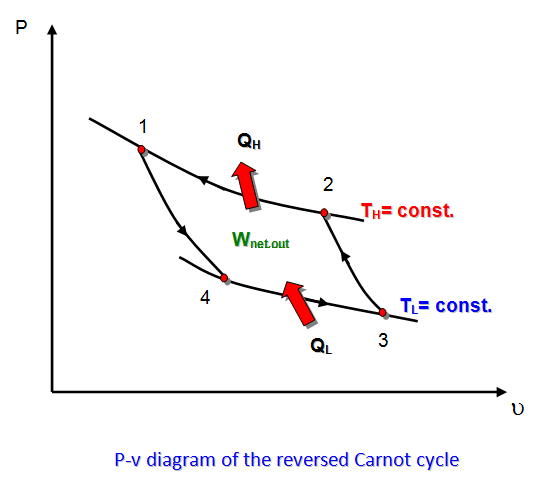
THE REVERSED CARNOT CYCLE
- The Carnot heat-engine cycle described above is a totally reversible cycle. Therefore, all the processes that comprise it can be REVERSED, in which case it becomes the CARNOT REFRIGERATION CYCLE. This time, the cycle remains exactly the same, except that the direction of any heat and work interactions are reversed: Heat in the amount of QL is absorbed from the low-temperature reservoir,heat in the amount of QH is rejected to a high-temperature reservoir, and a work input of Wnet,in is required to accomplish all this.
-
5.5 The Carnot Principles
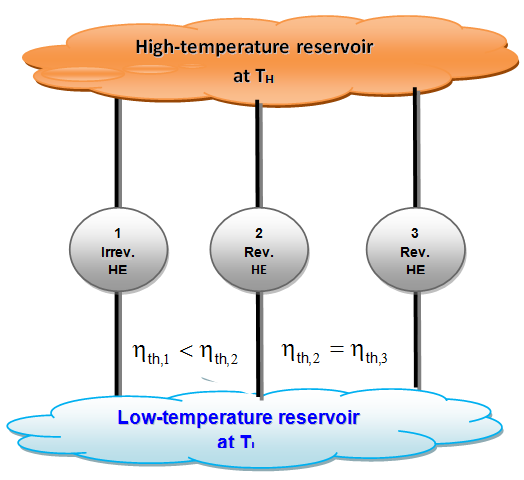
- The second law of thermodynamics places limitations on the operations of cyclic devices as expressed by the Kelvin-Planck and Clausius statements. A heat engine cannot operate by exchanging heat with a single reservoir, and a refrigerator cannot operate without a net work input from an external source.
- We can draw valuable conclusions from these statements. Two conclusions pertain to the thermal efficiency of reversible and irreversible heat engines, and they are known as the CARNOT PRINCIPLES. They are expressed as follows:
- 1. The efficiency of an irreversible heat engine is always less than the efficiency of a reversible one operating between the same two reservoirs.
- 2. The efficiencies of all reversible heat engines operating between the same two revervoirs are the same.
-
5.6 The thermodynamic Scale
- A temperature scale that is independent of the properties of the substances that are used to measure temperature is called a THERMODYNAMIC TEMPERATURE SCALE. Such a temperature scale offers great conveniences in thermodynamic calculations, and its derivation is given below using some reversible heat engine.
- The second Carnot principle discussed in Sec. 5.8 states that all reversible heat engines have the same thermal efficiency when operating between the same two reservoirs. That is, the efficiency of a reversible engine is independent of the working fluid employed and its properties, the way the cycle is executed, or the type of reversible engine used. Since energy reservoirs are characterized by their temperatures, the thermal efficiency of reversible heat engines is a function of the reservoir temperatures only. That is,
- \eta_{th, rev}=g(T_h,T_L)
- \frac{Q_H}{Q_L}=f(T_H,T_L)
- \eta_{th} = 1 - \frac{Q_L}{Q_H}
- Since. In these relations TH and TL are the temperatures of the high-and low-temperatures reservoir respectively.
- \left (\frac{Q_H}{Q_L}\right )_{rev}=\frac{T_H}{T_L}
- This temperature scale is called the KELVIN SCALE, and the temperatures on this scale are called ABSOLUTE TEMPERATURES.
-
5.7 The Carnot Heat Engine
- The hypothetical heat engine that operates on the reversible carnot cycle is called the CARNOT HEAT ENGINE. The thermal efficiency of any heat engine, reversible or irreversible, is:
- \eta_{th}=1 - \frac{Q_L}{Q_H}
- \eta_{th, rev} = 1 - \frac{T_L}{T_H}
- This relation is often referred to as the CARNOT EFFICIENCY since the Carnot heat engine is best known reversible engine. This is the highest efficiency a heat engine operating between the two thermal energy reservoirs at temperatures TL and TH.
- All irreversible heat engines operating between these temperatures limits will have lower efficiencies.

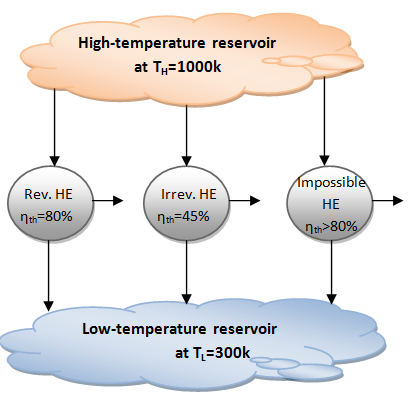
- No heat engine can have higher efficiency than a reversible heat engine operating between the same high- and-low-temperature
The Quality of Energy
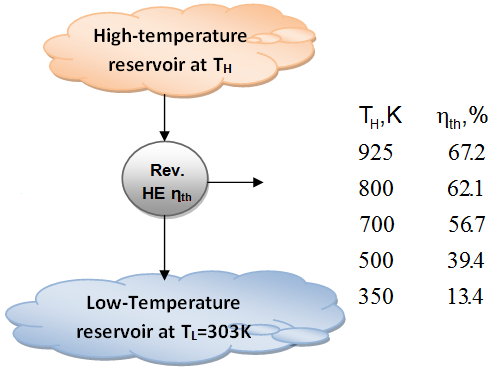
- The fraction of heat that can be converted to work is a function of source temperature (for TL=303K)
- These efficiency values show that energy has QUALITY as well as quantity. It is clear from the thermal efficiency values in figure before that more of the high-temperature thermal energy can be converted to work. Therefore, the higher the temperature, the higher the quality of the energy.
-
5.8 The Carnot Refrigerator and Heat Pump
- A refrigerator or a heat pump that operates on the reversed Carnot cycle is called a CARNOT REFRIGERATOR, or a CARNOT HEAT PUMP. The coefficient of performance of any refrigerator or heat pump, reversible or irreversible, is given as:
- COP_R=\frac{1}{Q_H/Q_L-1} \qquad \textrm{and} \qquad COP_{HP}=\frac{1}{1-Q_L/Q_L}
- The COP relation for reversible refrigerators and heat pumps become:
- COP_{R, rev} = \frac{1}{T_H/T_L-1} \qquad \textrm{and} \qquad COP_{HP,rev}= \frac{1}{1-T_L/T_L}

- No refrigerator can have a higher COP than a reversible refrigerator operating between the same temperature limits.
Example 5-2
- A Carnot heat engine receives 500 kJ of heat per cycle from a high-temperature heat reservoir at 652oC and rejects heat to a low-temperature heat reservoir at 30oC. Determine
- (a) The thermal efficiency of this Carnot engine.
- (b) The amount of heat rejected to the low-temperature heat reservoir.
- (a)
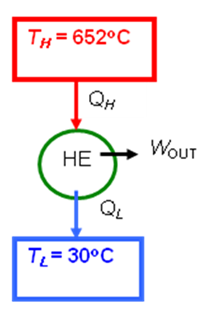
- \eta_{th,rev} = 1 - \frac{T_L}{T_H}
- = 1 - \frac{\left (30 + 273 \right )K}{\left (652 + 273 \right )K}
- = 0.672 \qquad \textrm{or} \qquad 67.2\%
- (b)
- \frac{Q_L}{Q_H}= \frac{T_L}{T_H}
- = \frac{\left (30 + 273 \right)K}{\left(652 + 273 \right )K}
- = 0.672 \qquad \textrm{or} \qquad 67.2\%
Example 5-3
- An inventor claims to have invented a heat engine that develops a thermal efficiency of 80 percent when operating between two heat reservoirs at 1000 K and 300 K. Evaluate his claim.
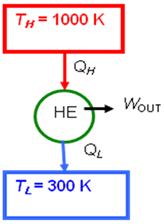
- \eta_{th, rev} = 1 - \frac{T_L}{T_H}
- = 1 - \frac{300K}{1000K}
- = 0.70 \qquad \textrm{or} \qquad 70\%
- The claim is false since no heat engine may be more efficient than a Carnot engine operating between the heat reservoirs.
Example 5-4
- An inventor claims to have developed a refrigerator that maintains the refrigerated space at 2oC while operating in a room where the temperature is 25oC and has a COP of 13.5. Is there any truth to his claim?
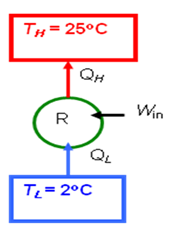
- COP_R = \frac{Q_L}{Q_H - Q_L} = \frac{T_L}{T_H - T_L}
- = \frac{\left ( 2+273\right )K}{\left (25-2 \right )K}
- = 11.96
- The claim is false since no refrigerator may have a COP larger than the COP for the reversed Carnot device.
Example 5-5
- A heat pump is to be used to heat a building during the winter. The building is to be maintained at 21oC at all times. The building is estimated to be losing heat at a rate of 135,000 kJ/h when the outside temperature drops to -5oC. Determine the minimum power required to drive the heat pump unit for this outside temperature.
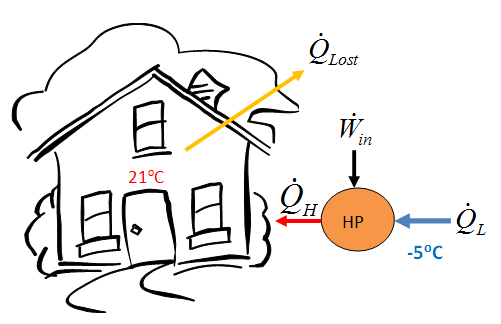
- The heat lost by the building has to be supplied by the heat pump.
- COP_{HP} = \frac{\dot{Q}_H}{\dot{W}_{net, in}}
- \dot{W}_{net, in} = \frac{\dot{Q}_H}{COP_{HP}}
- = \frac{135,000 kJ/h}{11.31} \frac{1h}{3600s} \frac{1kW}{kJ/s}
- = 3.316kW
- \dot{Q}_H = \dot{Q}_{Lost} = 135000 \frac{kJ}{h}
- COP_{HP} = \frac{\dot{Q}_H}{\dot{Q}_H - \dot{Q}_L} = \frac{T_H}{T_H - T_L}
- = \frac{\left(21 + 273 \right )K}{\left (21 - (-5) \right)K}
- = 11.31