Counters

Watch the Video  📹

● Ripple counters

– can be constructed using several forms of bistable
– consider the following arrangement
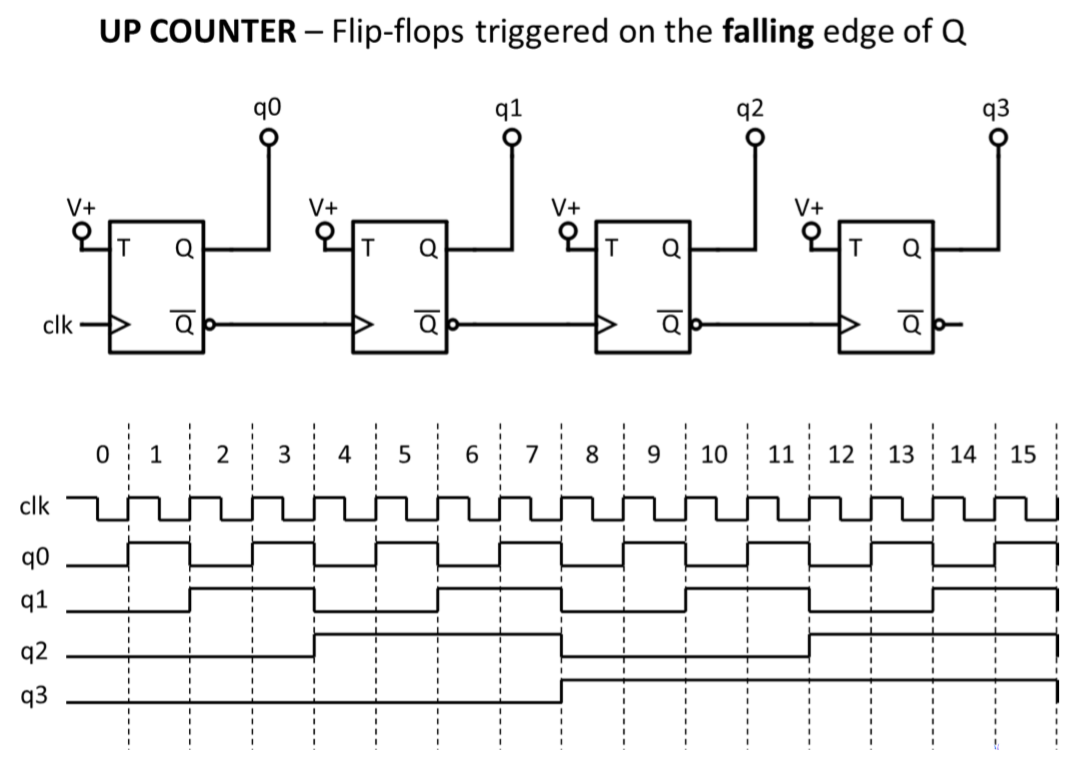
– with J = K = 1 each bistable toggles on the falling edge of its clock input





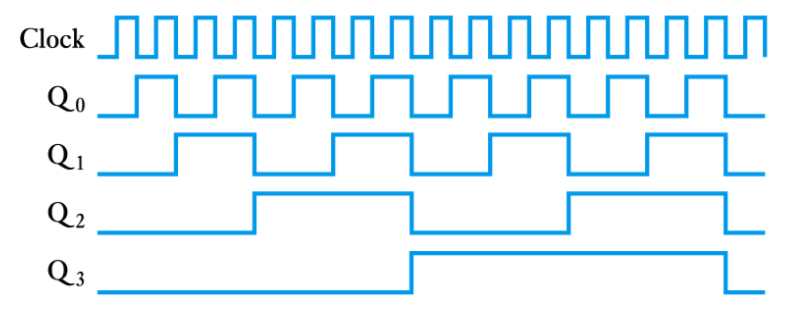
● Each stage toggles at half the frequency of the previous one
   –acts as a frequency divider
   –divides frequency by 2n (where n is the number of stages)

● A design example - see Example 25.4 in course text

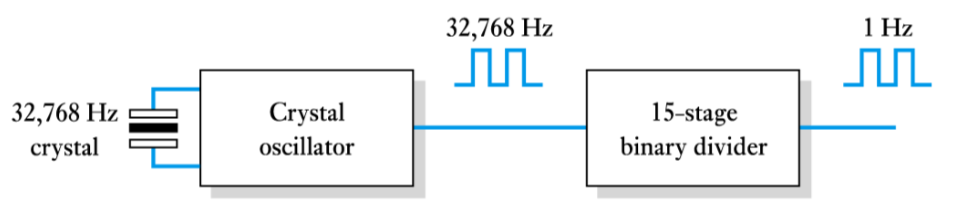
Clock generator for a digital watch
   –15-stage counter divides signal from a crystal oscillator by 32,768 to produce a 1 Hz signal to drive stepper motor or digital display


● Consider the pattern on the outputs of the counter shown earlier
   – displayed below
● the outputs count in binary from 0 to 2n−1 and then repeat
   –the circuit acts as a modulo-2n counter
   –since the counting process propagates from one bistable to the next this is called a ripple counter
   –circuit shown is a 4-bit or modulo-16 (or mod-16) ripple counter



● Modulo-N counters
–by using an appropriate number of stages the earlier counter can count modulo any power of 2
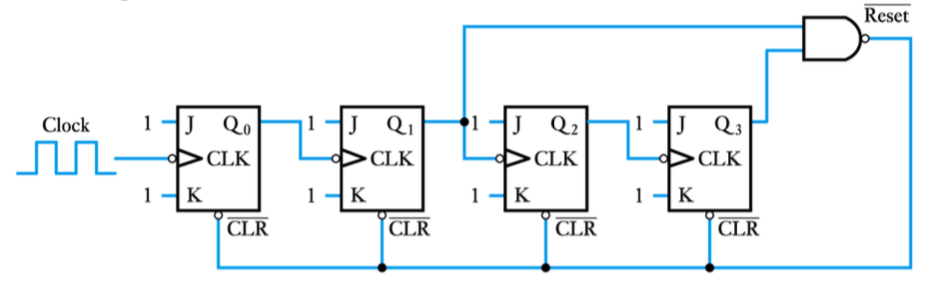
–to count to any other base we add reset circuitry
–e.g. the modulo-10 or decade counter shown here



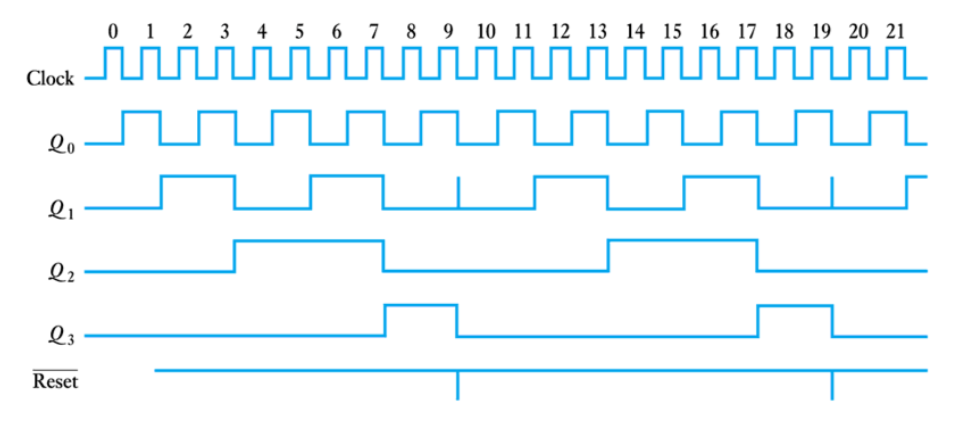
● Waveform diagram for the decade counter



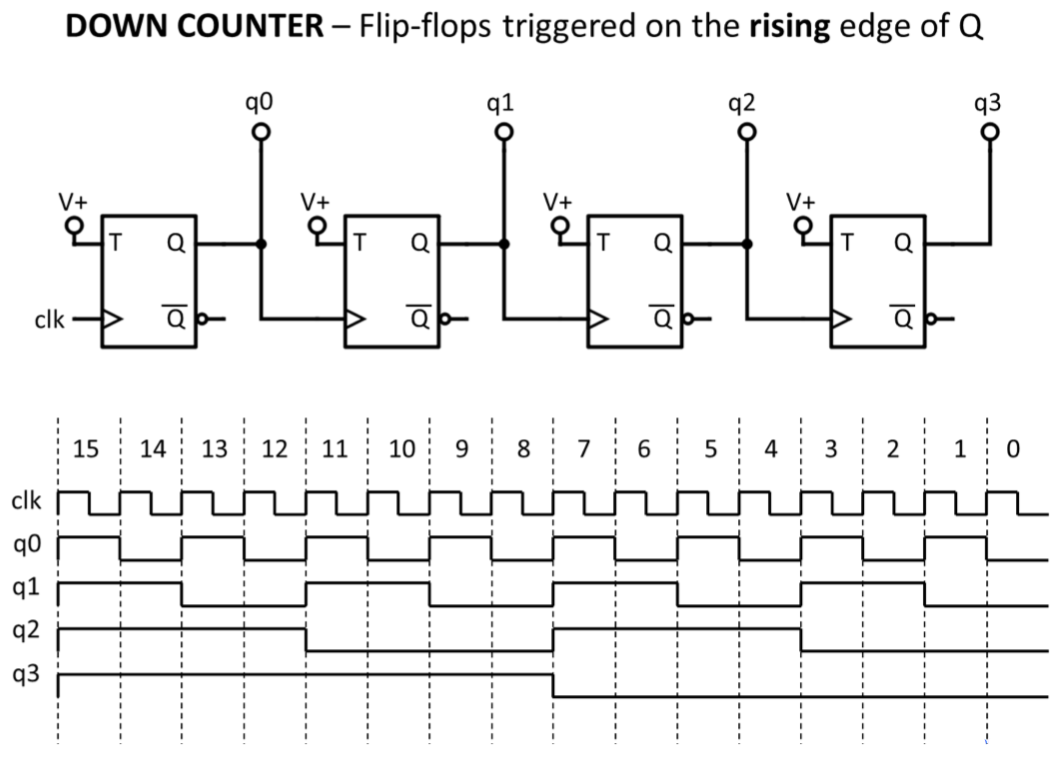
● A ripple down counters



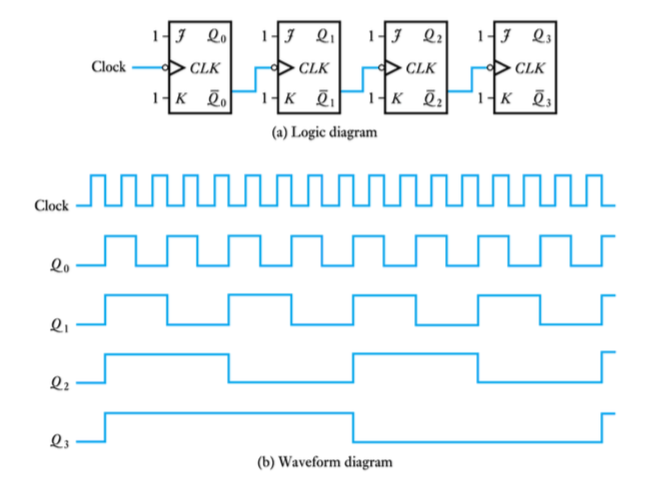
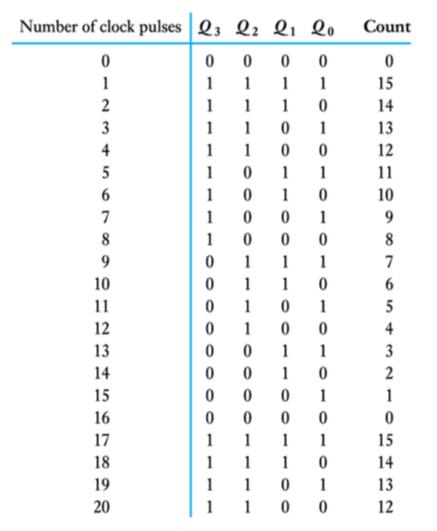
● The output sequence of the ripple-down counter



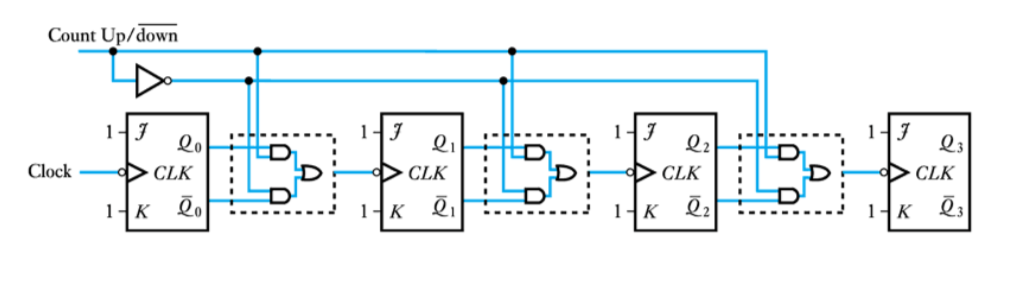
● An up/down counter

Review of Ripple Counters

● Ripple counters are just a CHAIN OF TOGGLE FLIP-FLOPS












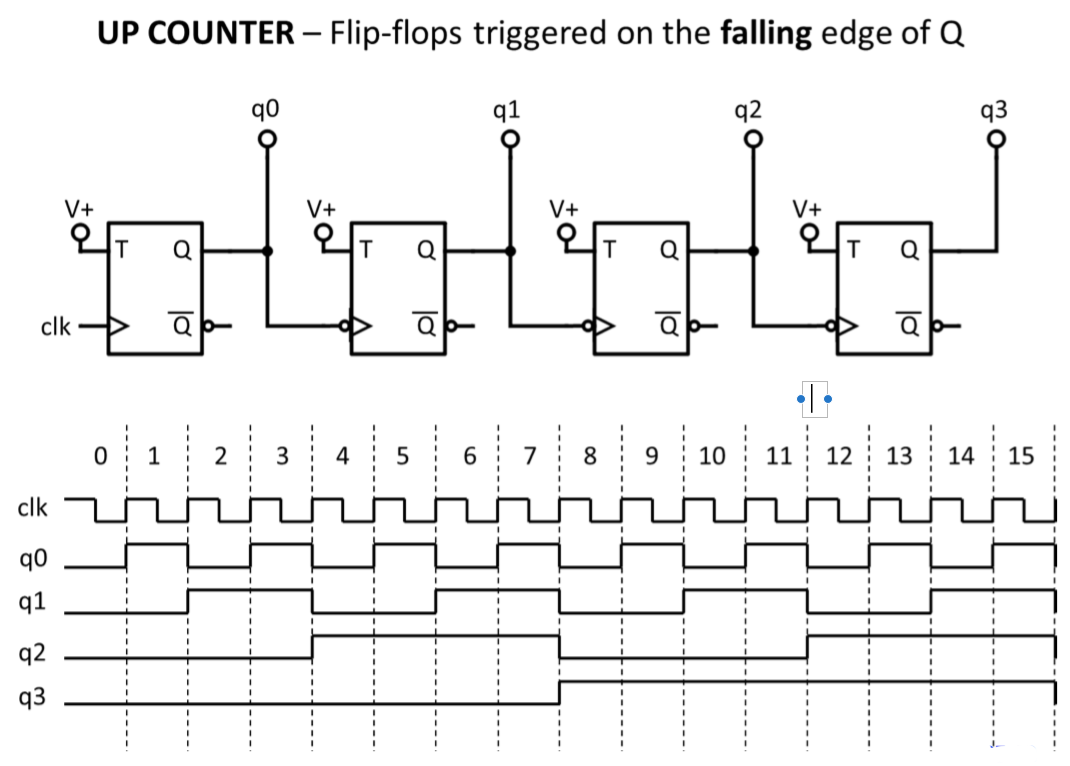
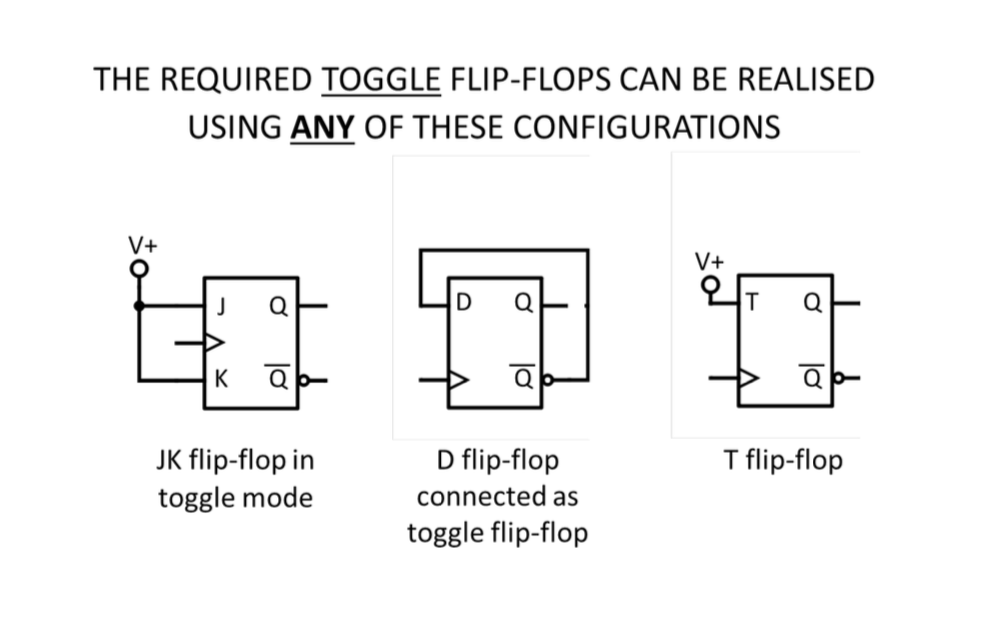
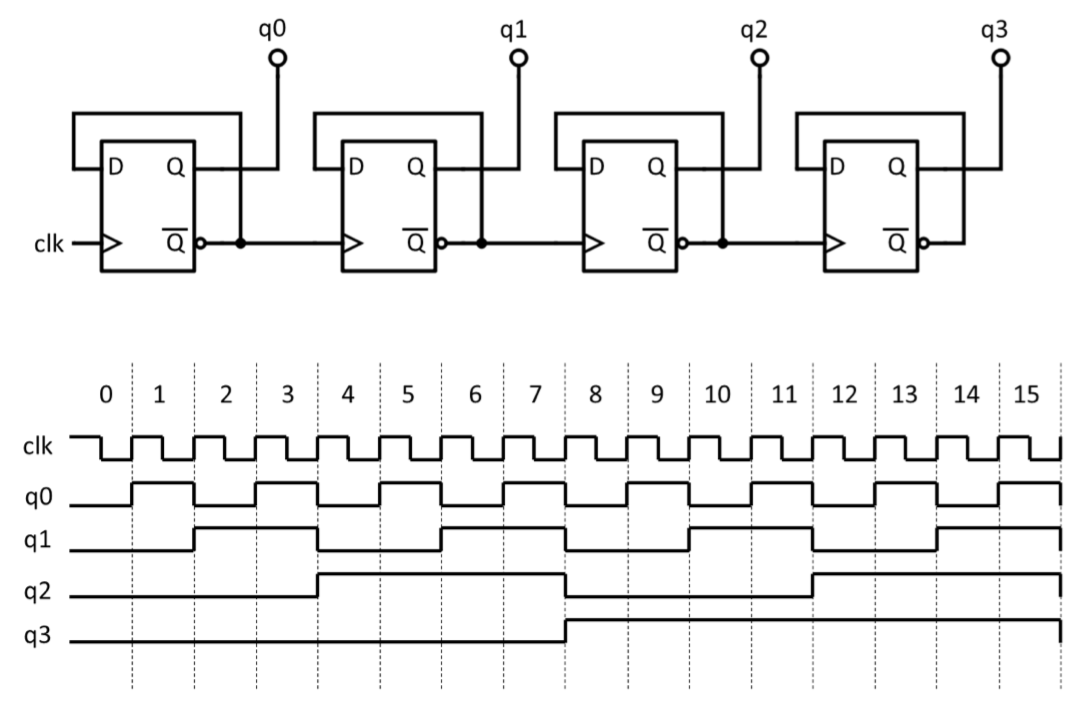
Ripple up-counter using D flip-flops




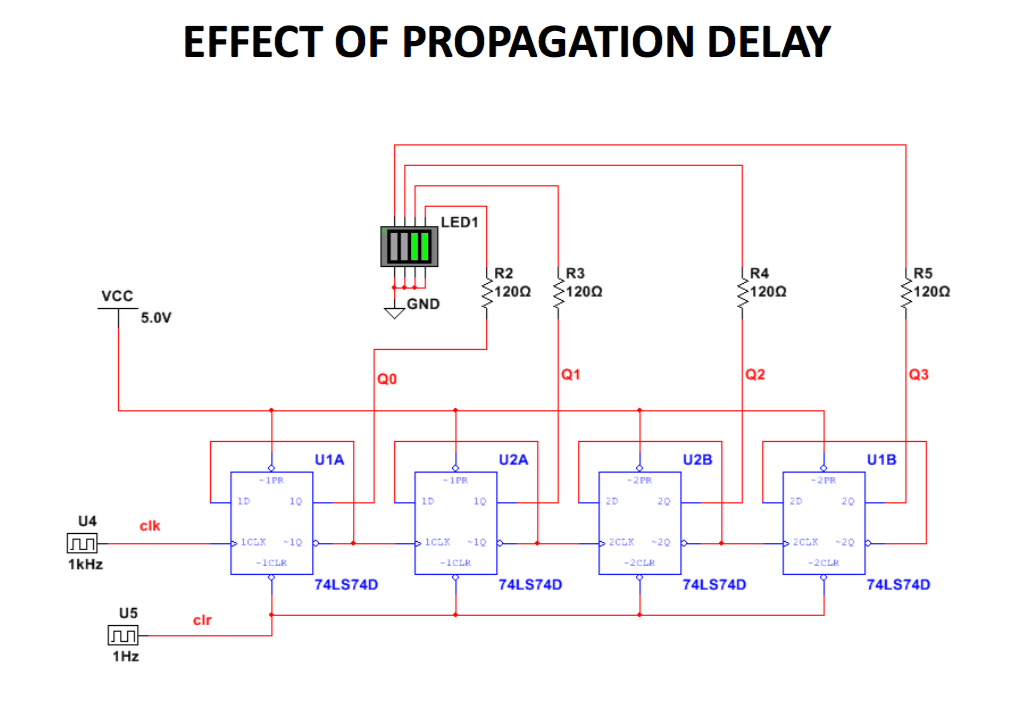
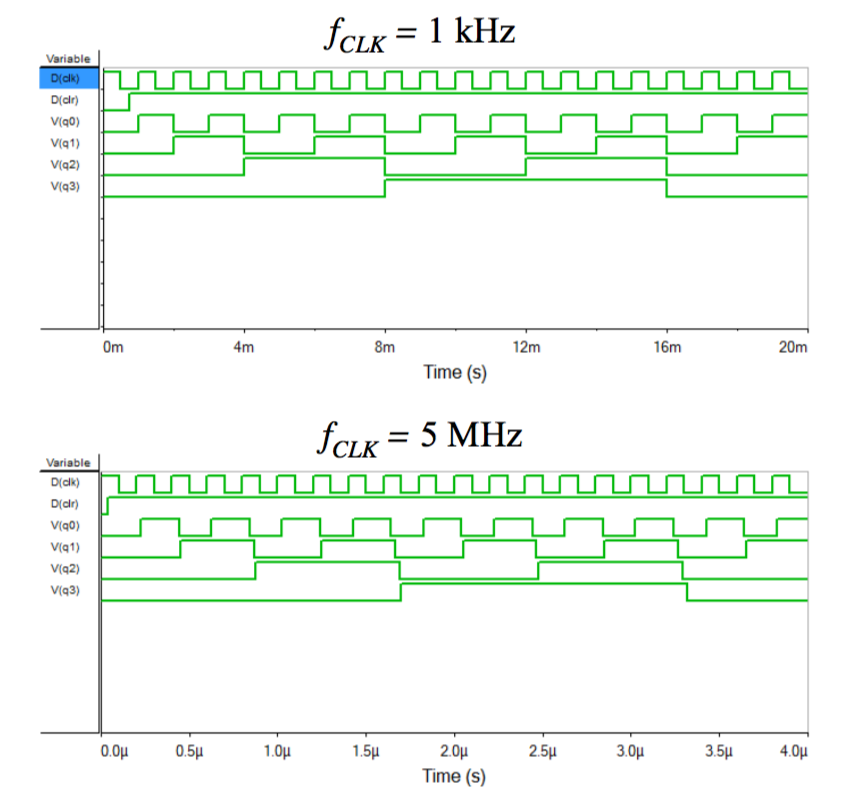
● Propagation delay in ripple counters
    – while ripple counters are very simple they suffer from problems at high speed
    – since the output of one flip-flop is triggered by the change of the previous device, delays produced by each flip-flop are summed along the chain
    – the time for a single device to respond is termed its propagation delay time tPD
    – an n-bit counter will take n x tPD to respond
    – if read before this time the result will be garbled





● Synchronous counters

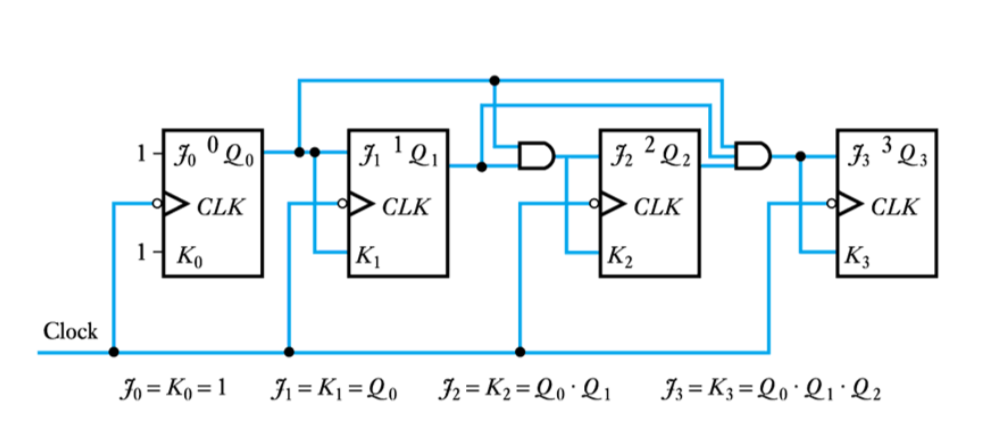
   – these overcome the propagation delay in ripple counters by connecting all the flip-flops to the same clock signal
   – thus each stage changes state at the same time
   – additional circuitry is used to determine which stages change state on each clock pulse
   – faster than ripple counters but more complex
   – available in many forms including up, down, up/down and modulo-N counters


● A synchronous four-stage counter


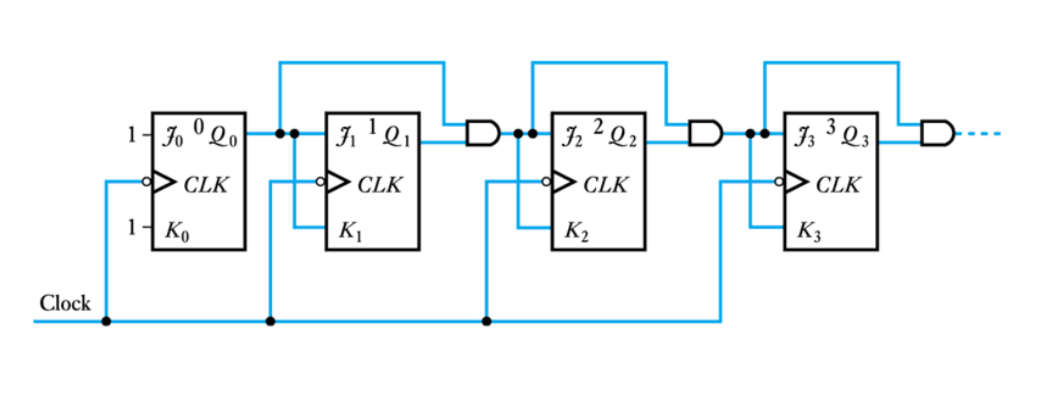
● A cascadable 4-bit synchronous counter




● Integrated circuit counters
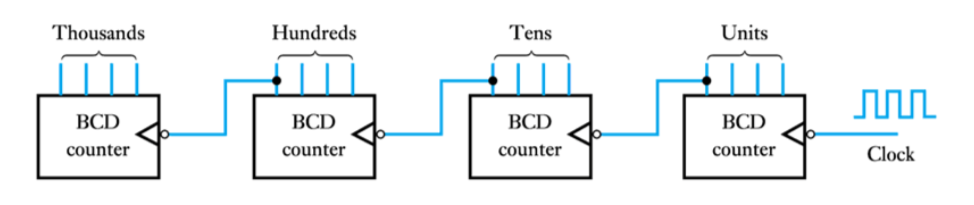
– while we can build counters from flip-flops, we more often use dedicated ICs
– these are available in numerous forms, such as binary, decade, BCD, up, down and up/down
– they are normally designed to simplify cascading

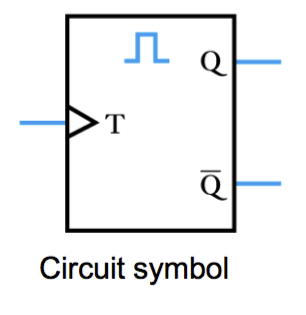
Monostables or one-shots

● Monostables are another form of multivibrator
    – while bistables have two stable output states
    – monostables have one stable & one metastable states ●when in its stable state Q = 0
      • when an appropriate signal is applied to the trigger input (T ) the circuit enters its metastable state with Q = 1
      • after a set period of time (determined by circuit components) it reverts to its stable state
      • it is therefore a pulse generator



● A simple monostable



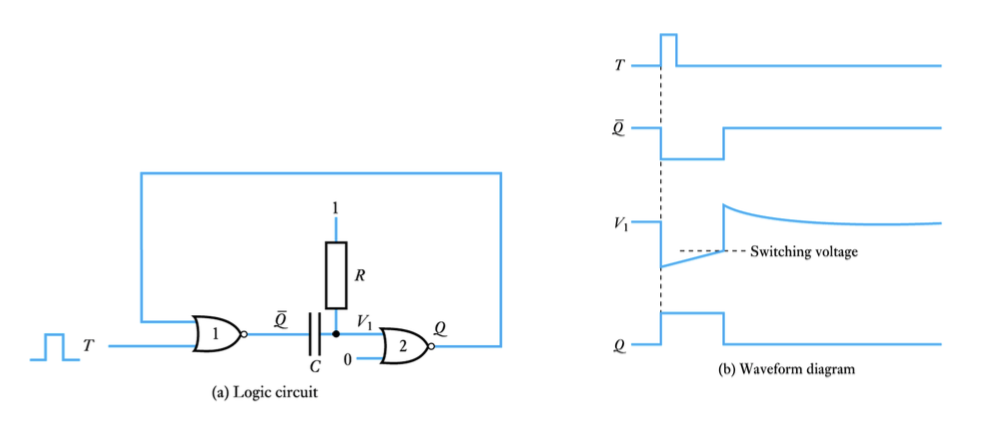
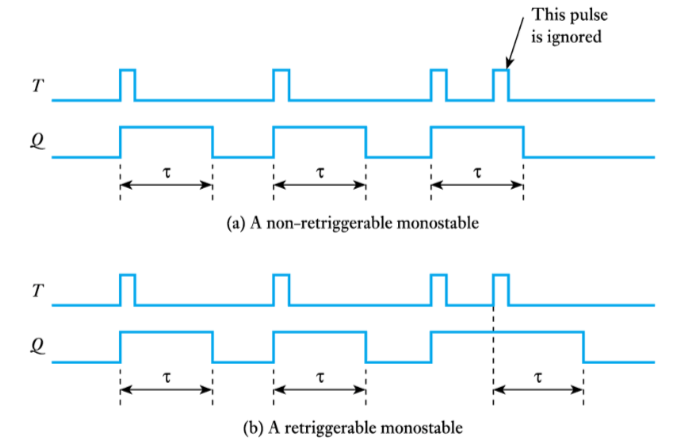
● Monostables can be retriggerable or non-retriggerable

Astables

● The last member of the multivibrator family is the astable
   –this has two metastable states
   –has the function of a digital oscillator
   –circuit spends a fixed period in each state (determined by circuit components)
   –if the period in each state is set to be equal, this will produce a square waveform


● A simple astable arrangement




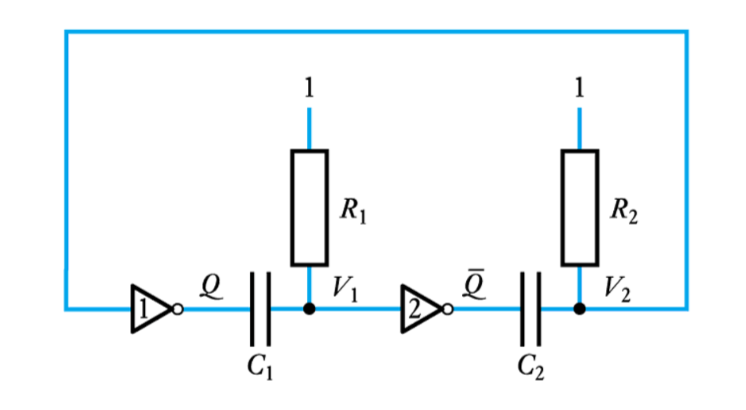
● Waveforms of the simple astable circuit





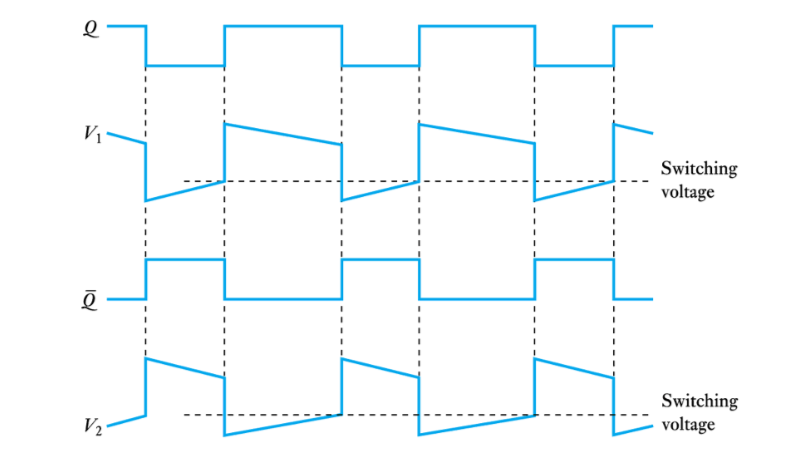
● An astable formed by two monostables

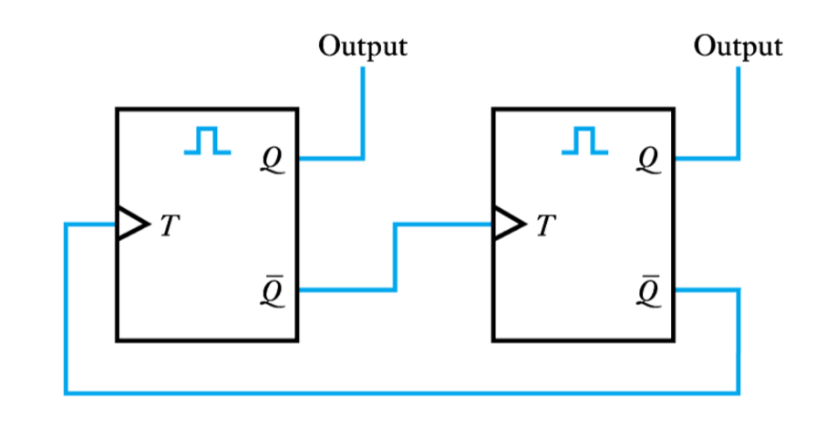
Memory Registers

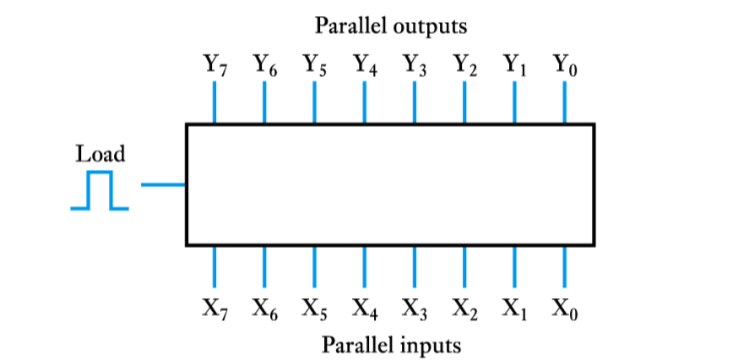
● Combining a number of bistables we can construct a memory register
   –several forms of bistable can be used, for example:



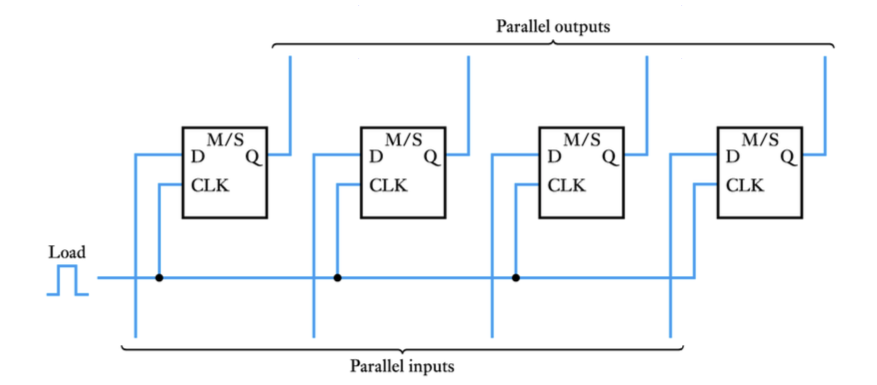
● Often we are not concerned with the internal construction of the register
   –they are a standard integrated component

Shift Registers

Watch the Video  📹

● The operation of a shift register

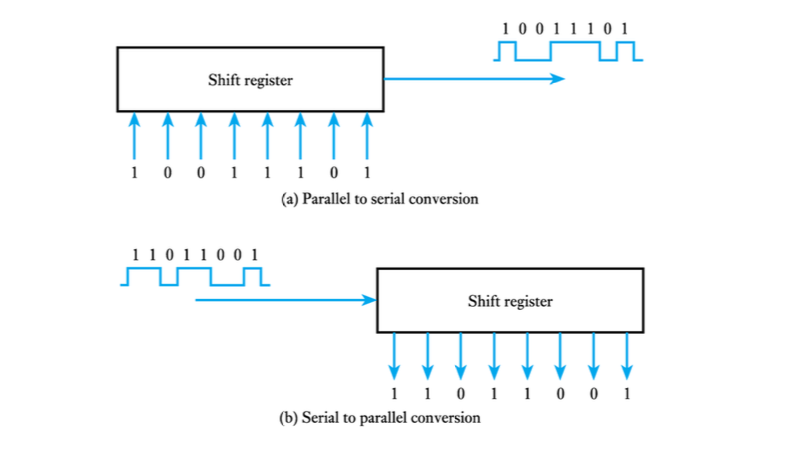
Shift Registers: A Chain of D Flip-Flops

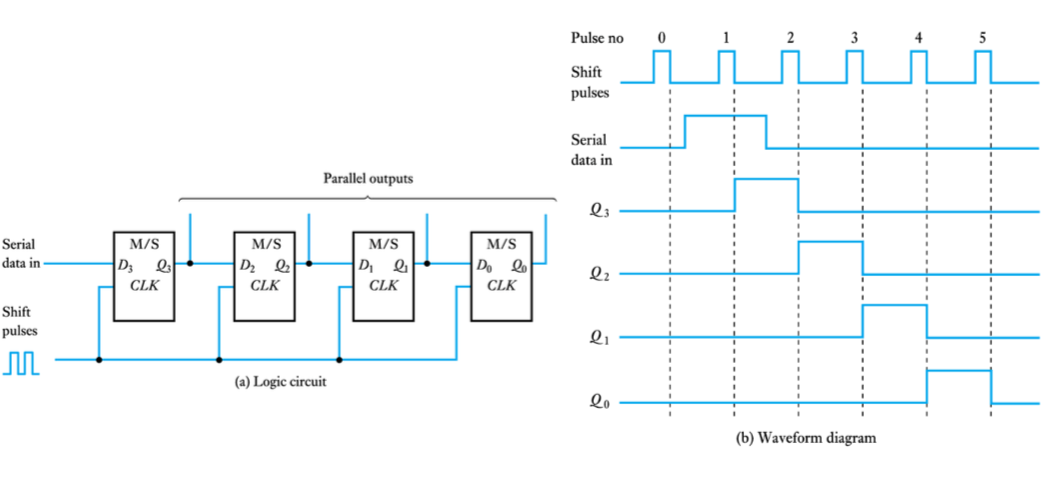
● A 4-bit parallel load shift register



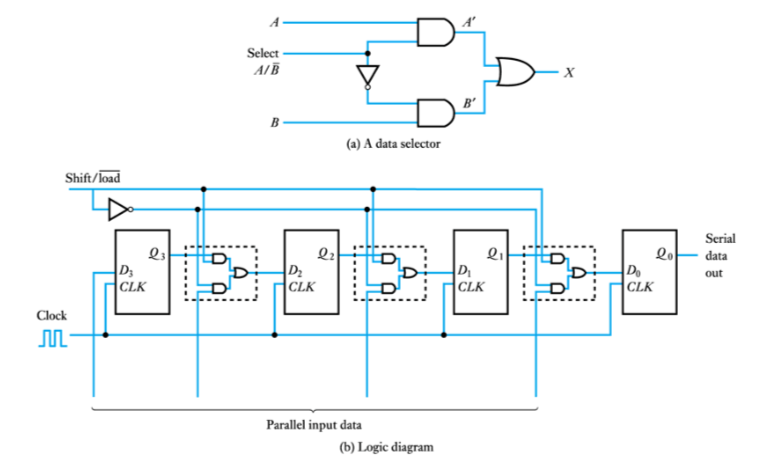
● A design example - see Example 25.3 in course text Application of a shift register

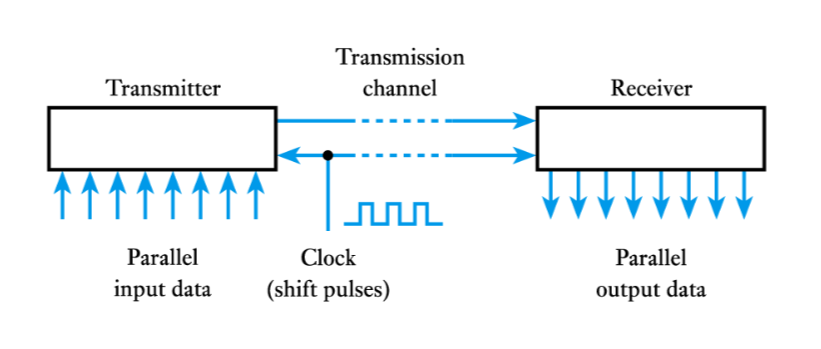
Application of a shift register
   –shift registers are widely used in communications systems

Key points

● Registers form the basis of various memories
● Counters are widely used in a range of applications
● Monostables and astables perform a range of functions