Introduction

Very often in order to solve a given programming problem we need to work with a collection of objects of the same type. A common form of collection is one that represents a sequence of elements. In mathematics a sequence is an enumerated collection of objects in which repetitions are allowed. The number of elements (possibly infinite) is called the length of the sequence. Enumerated simply means that the elements in the list can be listed one-by-one, and that the order of the elements matters. In programming a sequence is defined in much the same way (although not usually infinitely long!). There are many situations where it is useful to represent data as a sequence, for example a list of financial transactions, a list of students, and so on.
Depending on the programming task, we may have to apply different operations to a sequence of data, for example adding and removing elements or finding a specific element, or enumerating the elements in the list.
This week we will:: Recap the concept of abstract data types (ADTs) and data structures; Introduce the List ADT which is useful for representing sequences of data; Learn that the List ADT can have multiple different implementations and look at some of these
Recall that a data structure is a collection of data elements and the functions or operations that can be applied to the data. It can also represent relationships among the elements. Data structures can implement one or more ADT.
In general an ADT gives us a definition (abstraction) of the data structure. It specifies the characteristics and allowed operations without specifying in any implementation details. This allows an ADT to have several different implementations which can store the data in different ways.
This may not seem very important – if we can store the data in one way that lets us get the task done, why would we need different ways? In fact, this is often very important. Different data structures may allow the same operations, but the same operation may take much longer with one data structure than with another. For example, it might take twice as long, or more, to find a specific element in one List data structure than another, just because of the way the data is stored and hence the way it must be accessed.
The way an operation on a data structure performs depends on its efficiency. We will focus very much on the efficiency of data structures and algorithms throughout this module, and will shortly define what we mean by it.
It is common for a particular data structure to be very efficient for some operations, and less efficient for others. The best choice of data structure to implement an ADT often depends on the task, and on which operations are important for that task.
The sequence, or list, is one type of collection of data, but there are others. For example, sometimes we are not interested in the order of a collection of elements, but just want to know what unique elements are in the collection. In this situation the data is better represented by a data structure known as a set, which is an unordered collection of unique elements.
We can differentiate several main groups of data structures. Within each group there are several structures which are similar to each other but have their own specific characteristics. Some of these are listed in the table, and you will learn about many of these in this module.
Mastering basic data structures in programming is essential, as without them we could not program efficiently. They, together with algorithms, are the basis of programming and over the next few weeks you are going to become familiar with some of them.

List Data Structures

Probably the most commonly used data structures are the linear (list) data structures. They are an abstraction of all kinds of rows, sequences, series and others from the real world.

The List ADT

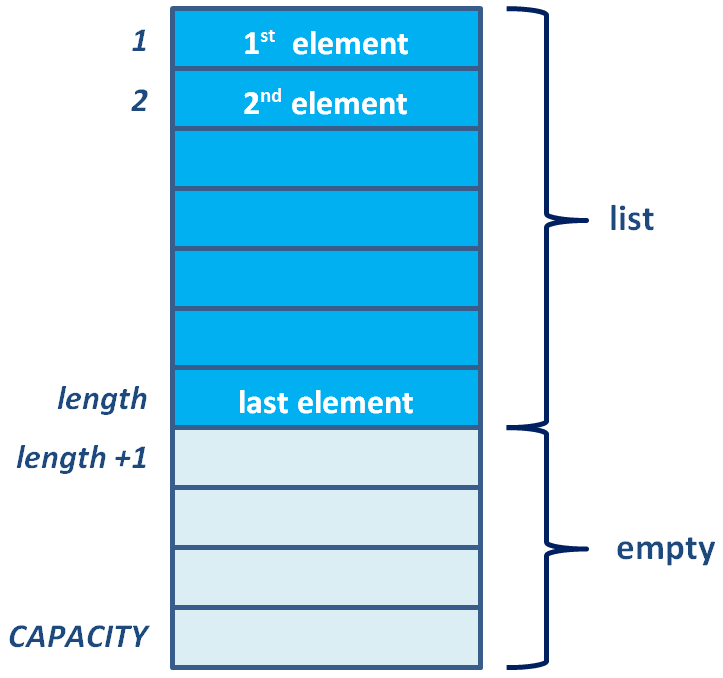
List is a linear data structure, which contains a sequence of elements

A1, A2, A3, …, AN

N is the property length of the list (count of elements) and its elements are arranged consecutively with Ai before Ai+1

A1: first element, AN: last element, Ai: position i

If N = 0 then the list is empty

The list allows adding or inserting elements at different positions, deleting them , traversing from start to end (for example to print the contents of the list) and searching to find a specific element.

can define the List ADT as follows:

Characteristics

Length identifies the number of elements in the list

Operations

Add an element to the list - insert

Delete an element from the list - remove

Show the elements in the list - printList

Find an element in the list - find

Create an empty list - createList

Implementation of the List ADT

As noted previously, there can often be more than one way of implementing an ADT, and this is true for the List ADT. To implement List we need to:

1. Choose an internal data structure, i.e. how we actually store the elements of the List

2. Figure out the algorithm needed for each of the major operations in the List ADT

3. For each operation, write a function or method to implement the algorithm

When choosing the internal structure, we should consider the following:

Each element needs to be stored as an individual data item

The storage must allow the characteristics of the List to be represented. Remember that elements are arranged consecutively, and each element has a position, or index, in the list.

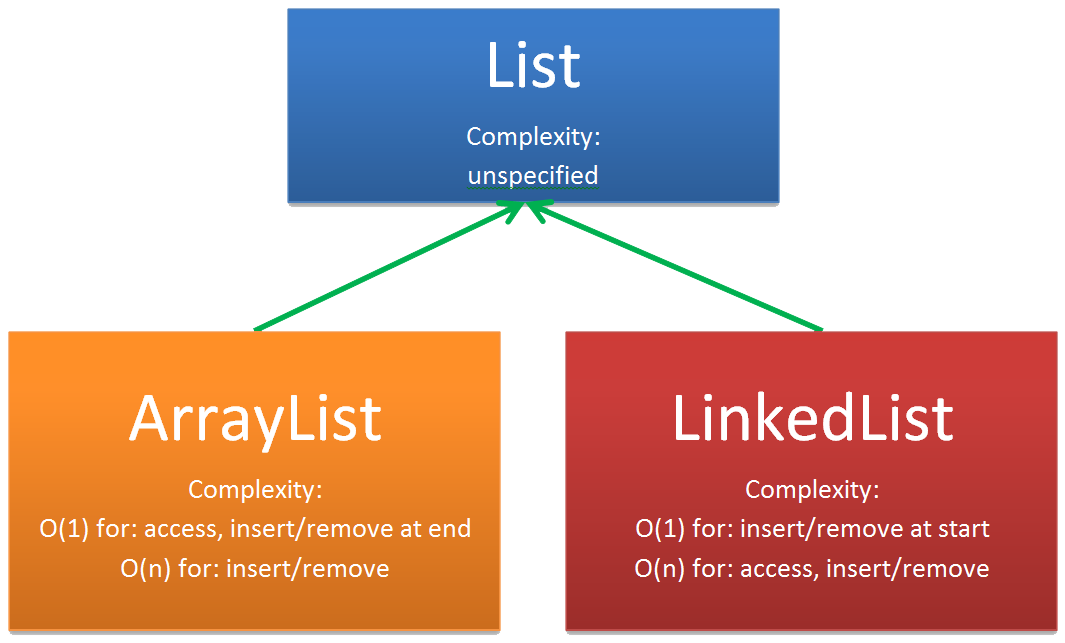
There are two standard implementations for the List ADT

Array list

Linked list

We will look at each of these, starting with the former as it is based on something you are already familiar with – the array. Note that an array in Java does not provide operations, so it is not a data structure, but it can provide a basis for implementing a data structure.
Array Implementation

Elements are stored in contiguous array positions

An array is an indexed structure. In an indexed structure:

elements can be accessed in sequence using a loop that increments the subscript – SEQUENTIAL order

elements may be accessed in any order using subscript values – RANDOM order

With a Java Array you cannot:

increase or decrease its length (length is fixed)

add an element at a specified position without shifting elements to make room

remove an element at a specified position and keep the elements contiguous without shifting elements to fill in the gap

If you implement a list by storing the data in an array, these characteristics need to be taken into consideration.

Firstly, you need to estimate how much data the list is likely to need to hold, i.e. the maximum size of the list. When the length of the list is less than the size of the array, the rest of the array will be empty. You might then encounter situations where that estimate is too low - if there is not enough space in the array then ‘fatal errors’ have to be guarded against. It is usual to overestimate the size - thus wasting space.

Secondly, you need to consider how well the operations will perform when implemented as an array. When you have only a small set of data then this doesn't matter much, but if you have a very large list then the time taken to perform the operations can become significant.
Efficiency of Array Operations

We express the efficiency, or complexity, of an operation in terms of how the time taken to perform it increases as the size of the data increases.

Take the printList operation – how much longer will it take to print a list of 10 elements than a list of 1 element? printList must work by traversing the list, one element at a time, and printing each element. Assuming each element takes the same time to print, it will take 10 times as long to print 10 elements as to print 1 element. It will take 100 times as long to print a 100 element list. In fact, if the list contains some number n elements, it will take n times as long to print as a single element list.

We say that the time taken grows linearly with the size, n, of the data. A useful shorthand for this is:

O(n)

In contrast, an operation that takes the same time no matter the size of the data is not dependent on n and is described as:

O(1)

This way of describing efficiency is known as Big O notation, and you will learn more about this later in the module.

The find operation on an array is done by traversing the list until a matching element is found. In the best case, the matching element is at the start of the list. In the worst case, the matching element is at the end, or not in the list at all. On average, it will be necessary to traverse half the length (n/2) of the list to find an element. If the list length doubles, then the average time will also double, so the time taken grows linearly. So find is also O(n)

insert and remove are also O(n)

e.g. insert at position 0 (making a new element)

requires first pushing the entire array along one position to make room

need to move all elements one-by-one

e.g. delete at position 0

requires shifting all the elements in the list back one position to fill the gap

These are the worst case positions for inserting/removing.

The best case is to add at the end or remove from the end - on average, half of the list needs to be moved for either operation

However, if you specifically need to add/remove at the end of the list, the efficiency of doing so is O(1)
Java ArrayList Class
Limitations of static arrays

Arrays are:

Simple,

Fast

but

Must specify size at construction time, which can't then change – static structure

Have to cater for possibility of under / over flow

"Murphy’s law"

Construct an array with space for n, where n = twice your estimate of largest collection….

Tomorrow you’ll need n+1

Need a more flexible/dynamic system.

The Java ArrayList class

The Java API provides implementations of a range of data structures, called the Collections Framework. These are in the package java.util, and include interfaces and classes that implement these. The List interface is implemented by classes that provide List data structures. Note that the names of the operations in the ArrayList class are a bit different from the List ADT we have defined here, and there are many more of them.

The simplest class that implements the java List interface is the ArrayList class. It uses an array to store the data in the list but overcomes the limitations of static arrays. It is a dynamic structure which can resize itself when it is nearly full. It does so by creating a new, larger array, copying the data to that, and discarding the old one.

The ArrayList class is particularly useful when:

you will be adding new elements to the end of a list

you need to access elements quickly in any order

Examples - using the ArrayList class

Need to import the ArrayList class and List interface:
```
import java.util.ArrayList;
import java.util.List;
```
To declare a List “object” whose elements will reference String objects (note that the ArrayList class is generic – it can store any kind of object, and you specify the type of object to store in <> when you create the ArrayList instance):
```
List<String> myList = new ArrayList<String>();
```
The initial List is empty and has a default initial capacity of 10 elements

To add strings to the list – the add operation places the new element at the end of the list:
```
myList.add("Glasgow"); 
myList.add("Edinburgh");
myList.add("Aberdeen");   
myList.add("Dundee");
```
📷 View Result

Adding an element with subscript 2:
```
myList.add(2, "Inverness");
```
📷 View Result

Notice that the subscripts of "Aberdeen" and "Dundee" have changed from [2],[3] to [3],[4]

When no subscript is specified, an element is added at the end of the list:
```
myList.add("Stirling");
```
📷 View Result

Removing an element:
```
myList.remove(1);
```
📷 View Result

The strings referenced by [2] to [5] have changed to [1] to [4]

You may also replace an element:
```
myList.set(2, "Perth");
```
📷 View Result

You cannot access an element using a bracket index as you can with arrays (array[1])

Instead, you must use the get() method:
```
String city = myList.get(2);
```
The value of city becomes "Perth"

You can also search an ArrayList:
```
int pos = myList.indexOf("Perth");
```
This returns 2 while
```
int pos = myList.indexOf("Paisley");
```
returns -1 which indicates an unsuccessful search

ArrayList also supports Java streams, which allows powerful searching using lambda expressions. The following example finds the first element that starts with “P”, so returns “Perth”:
```
String city = myList.stream().filter(
   s -> s.startsWith("P")).findFirst().get();
```
You can see the full documentation for the ArrayList class at 🔗 https://docs.oracle.com/javase/9/docs/api/java/util/ArrayList.html
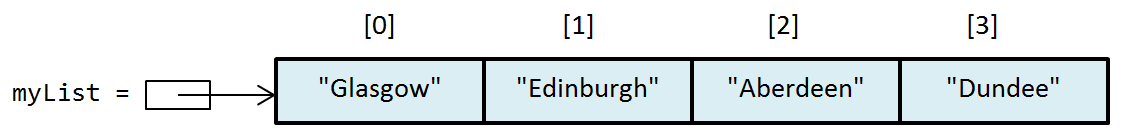x

x

x

x

x
A Simple List ADT and Array List Implementation
The Java Collections Framework classes are sophisticated, tried and tested implementations of common data structures. You would normally only create your own implementation if you need a structure that is not included in the Framework. However, it is useful to look at simpler implementations in order to understand the difference between different approaches. We will now look at a simple array list implementation to see how it works. We will look at the data storage and a couple of the operations.

First, let's define an interface to specify our List ADT– the characteristics and operations for this were stated earlier.
```
public interface ADTList {
    int length();
    void createList();
    String printList();
    void insert(String s);
    void remove(String s);
    boolean find(String s);
}
```
Note that this simple implementation will only store Strings, unlike the Collections Framework ArrayList class.

Now, let's look at part of an implementation of the ADTList interface. The data is stored in a field that is a String array, elements. The capacity of the array is stored as a constant, and the field length is the length of the list, i.e. the number of elements currently stored in the list:
```
public class SimpleArrayList implements ADTList {
    private String[] elements;
    private static final int CAPACITY = 10;
    private int length;
```
The length and createList method implementations are simple:
```
public int length() {
     return length;
 }

public void createList() {
    elements = new String[CAPACITY];
    length = 0;
}
```
This implementation of the insert operation adds a new element at the end of the list, if there is enough room, i.e. the new value goes into the first empty position in the array.
```
public void insert(String s)
{
    if (length < CAPACITY) {
        elements[length] = s;
        length++;
    }
}
```
This implementation operates in O(1) time, as the time taken does not depend on the length.

Another implementation of insert might add the new element at a specified position. This would require a loop to move the elements beyond that position along by one position to leave space for the new one, as shown in the code below. Note that the loop needs to count back from the end of the list to avoid overwriting elements.
```
public void insert(String s, int pos)
{
    if (length < CAPACITY) {
        for(int i=length-1; i>=pos; i--)
            elements[i+1] = elements[i];
        elements[pos] = s;
        length++;
    }
}
```
This implementation operates in O(n) time, as the number of times on average that the loop is executed, and hence the overall time taken, depends linearly on the length.

The remaining operations are left as a lab exercise.
Single Linked Lists

The other common list implementation is the linked list. This uses a completely different way of storing the data. As a result, its operations have different efficiencies to array lists.

A linked list is particularly useful for situations that require inserting and removing at arbitrary locations. The array list is limited because, as you have seen its insert operation operates in linear (O(n)) time except for the case of inserting at the end as it requires a loop to shift elements. The same is true for the remove operation.

A linked list, on the other hand, can add and remove elements at a known location in O(1) time. This is because of the way that a linked list works.

In a single linked list, which is the simplest case, instead of an index each element is linked to the following element. A linked list is like a chain of elements.

A linked list has flexible space use – instead of creating an array to hold all the elements, it can dynamically allocate space for each element as needed.

Linked list implementation

Each element of the list is implemented as a node. A node is an object that contains:

the data item

an reference or pointer to the next node

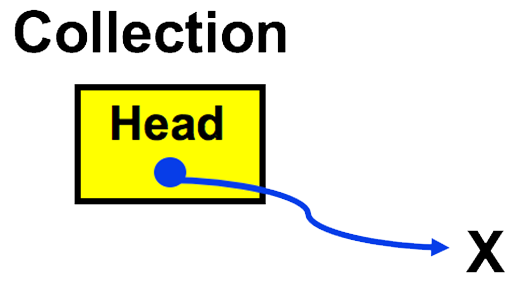
The list data structure has a reference to the first node of the list is known as the head. The data structure doesn’t directly reference any other elements of the list – these can be reached by following the references to successive nodes. In an empty list, before any elements have been inserted, the head is a NULL reference.

Here, X is used to represent NULL or an empty link, i.e. one that doesn’t point to anything

The last node of a list is known as the tail. There is no specific reference to the tail node in a singly linked list, but you will see another variation on the linked list that does have such a reference.
Java LinkedList Class

The LinkedList class in the Java Collections framework

The Java API Collections Framework provides a ready-made linked list implementation to use in your applications. Like the ArrayList class, it implements the List interface and is part of the package java.util.

As a result, it provides the same operations as ArrayList and its usage is the same. The examples of usage you saw previously for ArrayList will work with the ArrayList instance replaced with a LinkedList instance.

However, it is important to understand the efficiency of the operations on a linked list in order to choose the appropriate list implementation for an application. To help understand these, we will, as we did with the array list, look at a simple implementation of the List ADT and see how the data storage and some of the operations work.

You can see the full documentation for the LinkedList class at 🔗 https://docs.oracle.com/javase/9/docs/api/java/util/LinkedList.html
Single Linked List Implementation of Simple List ADT
Our simple linked list class should implement the same ADTList interface as our simple array list. However, this time we will use a variation on this interface that uses Java generics to allow any kind of object, not just Strings, to be stored. The type is referred to in the code by the placeholder type E, and the actual type is specified only in the application code that creates an instance of the list class that implements this interface. Note that the use of generics is not specific to linked lists - the SimpleArrayList class could have also been implemented with generics, but was done with Strings for simplicity in that first example.
```
public interface ADTListGeneric<E> {   
    int length();
    void createList();
    String printList();
    void insert(E e);
    void remove(E e);
    boolean find(E e);    
}
```
The linked list implementation consists of two classes. The first is a class Node, that represents a node of the list. Note that the type of the data item is the generic type E.
```
public class Node<E> {
    E data;
    Node<E> next; 
    
    Node(E e) {
        this.data = e;
        this.next = null;
    } 
}
```
The actual list data structure is represented by a class SingleLinkedList, which has a field to represent the head, which is a reference to a Node.
```
public class SingleLinkedList<E> implements ADTListGeneric<E> {
    private Node<E> head;
    private int length;

    public int length() {
        return length;
    }
    
    public void createList() {
        head = null;
        length = 0;
    }
```
An instance of the list can be created to hold String data as follows:
```
ADTListGeneric<String> strlist = new SingleLinkedList<String>();
sllist.createList();
```
You can create an instance to hold some other type of object, e.g. a class Person that you might have defined in your application:
```
ADTListGeneric<Person> personlist = new SingleLinkedList<Person>();
personlist.createList();
```
Single Linked List Operations - Inserting and Finding
Inserting an item at the beginning of the list

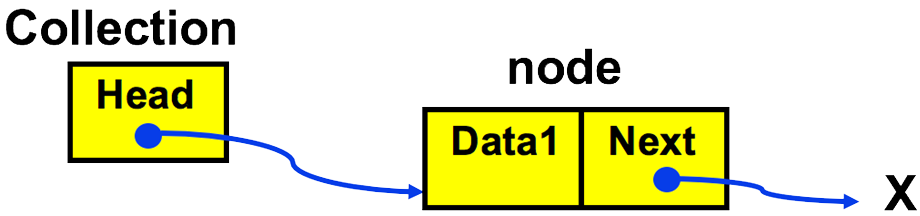
Inserting first item to an empty list:

1. Allocate space in memory for node

2. Set its data item

3. Set Head to point to new node

Insert a second item – this involves “breaking” the link between the head and the first node, inserting the new node, and creating links to position the new node in the “chain”

1. Allocate space in memory for new node

2. Set its data item

3. Set the new node’s Next to current first node

4. Set Head to point to new node

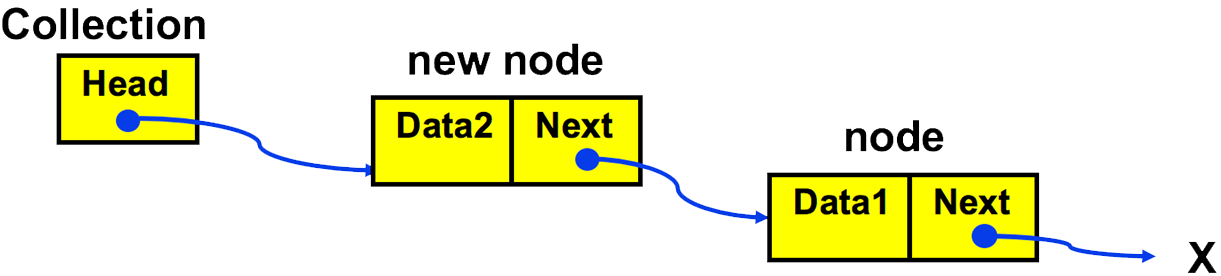
This algorithm for insert at the start of a linked list is the same no matter how many elements are in the list as the rest of the list past the first node is not involved, so this operates in O(1) time.

The algorithm can be implemented as follows. Note that this works for both empty and non-empty list cases:
```
public void insert(E item) {
    Node<E> tmp = new Node<E>(item);
    tmp.next = head;
    head = tmp;
    length++;
}
```
Finding a specified item

To find an item we need to traverse the list from the head until we reach an element whose data item matches what we are looking for. Traversal is done by creating a temporary node reference that initially points to the first node in the list, i.e. the same node as the list head points to. The algorithm is as follows:

1. Create temporary node reference that points to the first node in the list

2. While (the temporary node is not pointing to the last node or to null)

3. Check whether the data item is the one we want and return true if it is

4. Set the temporary node to point to the next node

The implementation is as follows. validAccess is a private method that encapsulates the while condition.
```
public boolean find(E e) {
    Node<E> tmp = head;

    while (validAccess(tmp)) {
        if (e.equals(tmp.data)) {
            return true;
        }
        tmp = tmp.next;
    }
    // to get here we fell off the end of the list 
    // so can’t be in the list
    return false;
}

private boolean validAccess(Node<E> node){
    if(node == null)
        return false;
    if(node.next == null)
        return false;
    return true;
}
```
Traversing, on average, depends linearly on the list size, so this operates in O(n) time.

Note that this implementation of find simply tells us whether a data item is present. Alternatively, we could implement it so that it returns the data item itself.

Inserting an item at a specified other position in the list

This is very similar to inserting at the start of the list, but with the additional requirement to find that position in the list first:

1. Traverse the nodes to get to the position where the item is to be added (remember that this is not an array, you can’t go directly to an element by index)

2. Allocate space in memory for new node

3. Set its data item

4. Set the new node’s Next to node currently in the specified position

5. Set the previous node’s Next to point to new node (you have to keep a reference to the previous node and update it each time you move to the next node)

The actual insertion of the node operates in O(1) time as before, but the time to find the position by traversing, on average, does depend linearly on the list size, so operates in O(n) time.

You can look at the implementations of insert and find which you have seen, and the implementation of remove which follows, to work out how to implement this version of insert.

Group	Common characteristic	Specific example(s)
Linear	Ordered sequences	list, stack, queue
Dictionary	Key-value pairs	hash table
Tree	Hierarchical tree structure	binary tree, B-tree, AVL tree, red-black tree
Set	Unordered collection of unique elements	hash set
others		multi-set, bag, multi-bag, priority queue, graph, …

Single Linked List Operations - Removing and Traversing

The algorithms for removing an item is similar to inserting.
To remove the first item, we simply change the head to refer to the next (second) element. The rest of the list is not involved, so this operates in O(1) time.

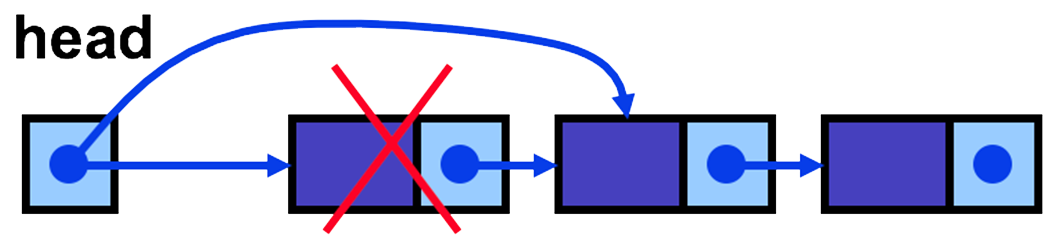
public Node<E> removeFirst() { Node<E> tmp; if (validAccess(head)) { tmp = head; head = head.next; length--; } else { // list is empty tmp = null; length = 0; } return tmp; }
To remove an item at a specified position, we need to traverse the list to find that position, and then change the next reference of the previous node to point to the next node instead of the current one.

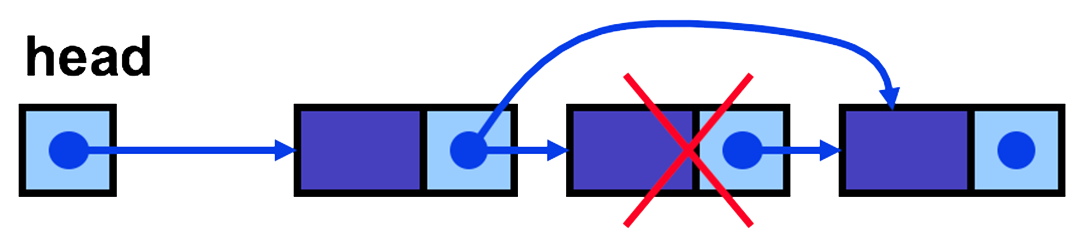
The actual removal of the node operates in O(1) time as before, but the time to find the position by traversing, on average, does depend linearly on the list size, so operates in O(n) time.
The following code implements both cases:
public void remove(E e) { Node previous = null; Node current = head; while (validAccess(current)) { if (e.equals(current.data)) { // found the node that needs to be removed if (previous == null) { // must be removing the first node in the list head = current.next; } else { // removing a node that’s not first in list previous.next = current.next; } current = null; } else { previous = current; current = current.next; } } }
Simple traversal of the list is similar to the traversal you have already seen for finding and removing elements.
public String printList() { StringBuilder listString = new StringBuilder(); int count = 0; Node<E> tmp = head; while (validAccess(tmp)) { listString.append(String.format("(%d) ==> %s ", count, tmp.data.toString())); tmp = tmp.next; count++; } listString.append(String.format("(%d) ==> %s ", count, tmp.data.toString())); return listString.toString(); }
Storage:
Uses only as much memory as needed for the elements in the list. Requires no estimate of the maximum size of the list, so no wasted space as there is in the array implementation. However, each item requires more memory space than an item in an array as the reference to the next node also needs to be stored.

Variation of the Linked List
Circular Singly linked lists

The last node points to the first node of the list.

Different implementations are possible – can have a reference to the head and/or the tail.

If implemented without a tail reference, how do we know when we have finished traversing the list? Needs additional code: could use size() of the current list or check against Head node twice!

Circular lists are useful in applications to repeatedly go around the list, for example:

keeping track of who is next to play in a game

representing stops in the Glasgow subway (if you live in Glasgow, you’ll understand this right away, if not take a look at the map at 🔗 http://www.spt.co.uk/subway/maps-stations/)

Doubly linked lists

Limitations of a singly-linked list include:

Insertion at the front is O(1) but insertion at other positions is O(n)

Insertion is convenient only after a referenced node has been found

Removing a node requires obtaining a reference to the previous node

We can traverse the list only in the forward direction

We can overcome these limitations:

Add a reference in each node to the previous node, creating a double-linked list

Can modify Node class definition to include a prev reference as well as the existing next reference

Each node points to not only successor but the predecessor

There are two NULL (𝜙): at the first and last nodes in the list

Advantage: given a node, it is easy to visit its predecessor. Convenient to traverse lists backwards
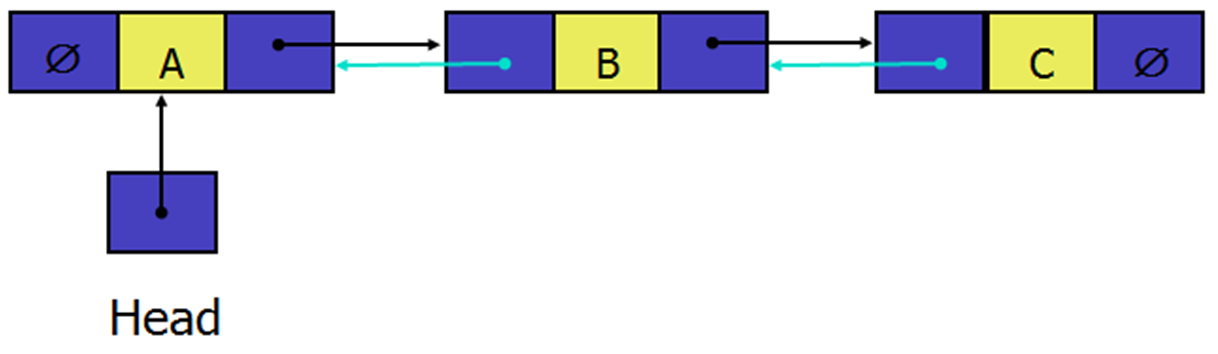
```
public class Node<E> {
E data;
Node<E> prev;
    Node<E> next; 
    
    Node(E e) {
        this.data = e;
	  this.prev = null;
        this.next = null;
    } 
}
```
As with the single-linked class, the actual list data structure is represented by a class which has the following fields:

head (a reference to the first list Node)

tail (a reference to the last list Node)

length
```
public class DoubleLinkedList<E> implements ADTListGeneric<E> {
    private Node<E> head;
    private Node<E> tail;
    private int length;
```
Because we have a reference to the tail, and the last node has a reference to the preceding node, insertion at the end is very similar to insertion at the beginning, and can be done without traversing. Insertion at either end is therefore O(1). However, insertion elsewhere is still O(n) as traversal is needed to reach any other position.

Array implementation of linked lists

It is possible to implement a linked list in a different way, using either a two dimensional array or two separate arrays. In this implementation, one array (or dimension) stores the data items while the other stores the index of the next data item.

As a single linked list the data structure has to hold a head reference. Here, the head is simply the index of the first item in the data array.

What word would the contents of the data array, in list order, spell out for the following example?

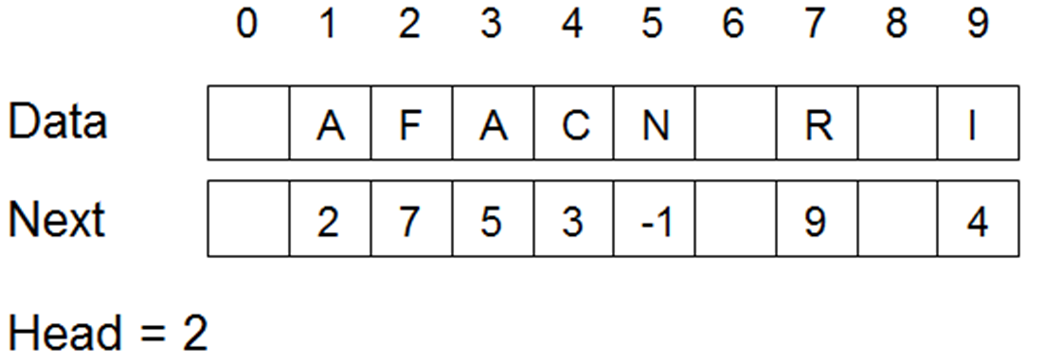
As items are inserted and removed this data structure also needs to keep track of what positions in the array are free. This can be done with using the same arrays. The data structure then needs a First reference that contains the index of the first free position in the data array, and the other array is used to build up a list of free positions.

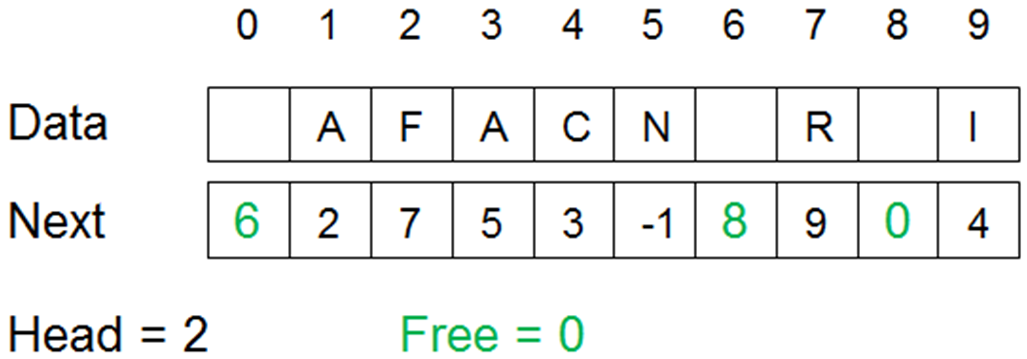
The efficiency of this is similar to the linked list based on nodes. This implementation might be useful if you want a fixed limit to the size of the list rather than a dynamic structure.
Iterators
You have seen that traversal works in different ways in each of our simple list implementations. In the array list we can use a for loop to iterate through the array elements. In the linked list we can use a while loop and follow references from node to node until we reach the end of the list.

The Java Collections Framework implementations offer a more consistent approach to traversal so that application code can traverse the list and do so using the same interface in each case. They do so by providing an iterator object.

An iterator can be viewed as a moving place marker that keeps track of the current position in a particular linked list

An Iterator object for a list starts at the first node

The programmer can move the Iterator by calling its next method. The programmer doesn't need to know anything about the internal working of the data structure and how to move from one element to the next, the Iterator provided by the list encapsulates that knowledge

The Iterator stays on its current list item until it is needed

An important advantage of iterators in Java is that if a collection can provide an iterator then it can be used with the enhanced for loop, for example:
```
for (String s : myList){
	System.out.println(s);
}
```
Many different data structure classes can provide iterators, each with a knowledge of their data structure but with a common programming model by implementing the interface Iterator. A class indicates that it can provide an iterator by implement the interface Iterable.

See this week's Further Reading for more information on iterators.
Relationship of the List ADT to Implementations and Other Data Structures

Implementation Hierarchy

A list data structure can be implemented in different ways:

Specialisation Hierarchy

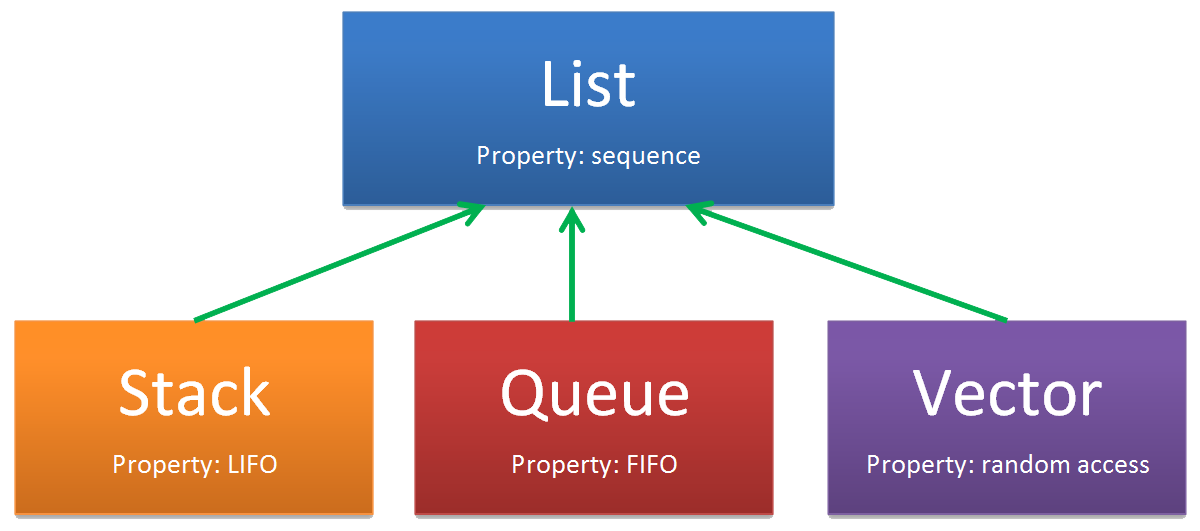
List can be the basis for other more specialized data structures, some of which you will study later in the module. These are based on sequences of data, but have more specific access rules, e.g. last-in-first-out (LIFO).
Summary: Array List Versus Linked List

Storage

Array List:

Static

The size of a Java array is fixed at compilation time

Wasted space if list data does not fill array

Can only resize by copying data into a new array

Linked List:

Dynamic

Don’t need to know how many nodes will be in the list, they are created in memory as needed

No wasted space, although references within nodes take up some memory

A linked list can easily grow and shrink in size

Performance

Array List:

Time to access does not depend on the size of the list – O(1)

To add/remove an element at the end of the list, the time taken does not depend on the size – O(1)

Time taken to add/remove an element at any other point in the list, on average, does depend on the size – O(n)

Linked List:

Time to access, on average, depends on the size of the list – O(n)

To add/remove an element at the start of the list, the time taken does not depend on the size – O(1)

Time taken to add/remove an element at any other point in the list, on average, does depend on the size – O(n)