Stacks share many of the characteristics of lists, except they have a restriction on where data must be accessed or stored (only at the top).

Data in stacks is homogeneous, i.e., all data items are of the same type (note that because of polymorphism, the items can be of the stack element type or any sub-type of that type)

We can use list-type implementations for stacks

Arrays (static/fixed datastructure)

Linked lists (dynamic datastructure)

Array-based stack (version 1)

Problems

The top is fixed, therefore all access for storage (push) or retrieval (pop) must go through it.

To keep it LIFO, the most recent item must be on top

As new items are added older items must shuffle down.

This is slow and unnecessary

A better implementation

Instead of fixing the top and moving the data, fix the data and move the top

As long as we know where top is we can still do all push and pop functions associated with LIFO

Array-based stack (version 1) – floating top

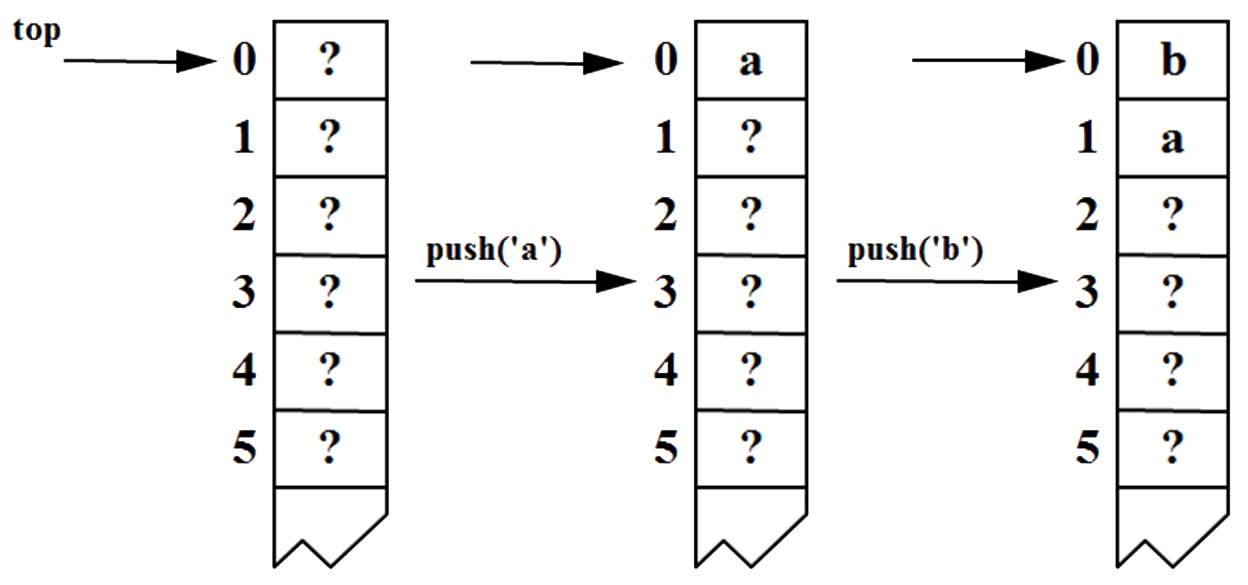
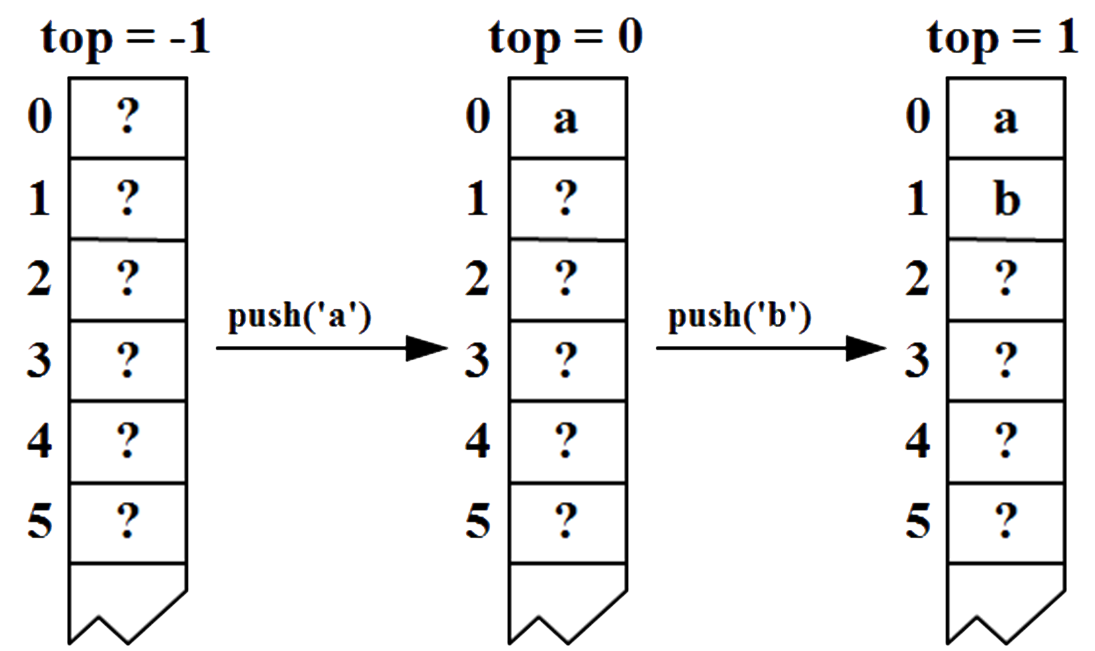
Stack creator (constructor)

// set up the stack top
begin createStack( )
   set stackTop to lowest array index  -1;
end createStack;

push( ) algorithm – array

// function to push an item onto the stack
begin push( stackElement se )
   if ( stackFull ) begin
      print "Stack is full\n";
      set ok to false;
   end
   else begin
      inc stackTop;
      set stack[ stackTop ] = se;
      set ok to true;
   end if
   return ok;
end push;

pop( ) algorithm – array( )

// function to pop the top item from the stack 
begin pop( stackElement se)
   if ( stackEmpty ) begin
      print "Stack is empty\n";
      set ok to false;
   end
   else begin
      se = stack [ stackTop ];
      dec stackTop;
      set ok to true;
   end if
   return ok;
end pop;

stackEmpty( ) and stackFull( )

// function checks to see if the stack is empty
begin stackEmpty( )
   return stackTop == minStackSize;
end stackEmpty;

// function checks to see if the stack is full
begin stackFull( )
   return stackTop == maxStackSize;
end stackFull;

Standard notation for arithmetic expression is called ‘infix’. The operator is ‘in between’ pairs of operands.

Example:

5 + 7

A problem that arises with infix notation is possible ambiguity - which operator is carried out first when there is more than one operator in an expression?

5 + 7 / 2

Precedence rules

Infix ambiguity is solved by precedence rules

1. Evaluate expressions in parentheses first

2. * and / before + and -

3. Equal precedence goes left to right

These rules are sometimes known as BODMAS

Brackets (parts of a calculation inside brackets always come first)

Orders (numbers involving powers or square roots).

Division

Multiplication

Addition

Subtraction

Other forms of expressions

Infix is only one method of representing expressions. Others are ‘postfix’ and ‘prefix’

In postfix expressions the operators come after operand pairs (5 7 +)

In prefix expressions the operators come before operand pairs. (+ 5 7)

Reverse Polish Notation

RPN is a postfix expression form. It requires no parentheses. It does require a stack to evaluate expressions.

Rules of evaluation:

1. Evaluate from left to right

2. When you encounter an operator you immediately apply it to the operands that preceded it. Then put the result on the stack.

Tokenization

Input characters are either operators or operands. Each is evaluated as a ‘token’ and the appropriate action taken for that token.

This process is called ‘tokenization’ or ‘lexical analysis’

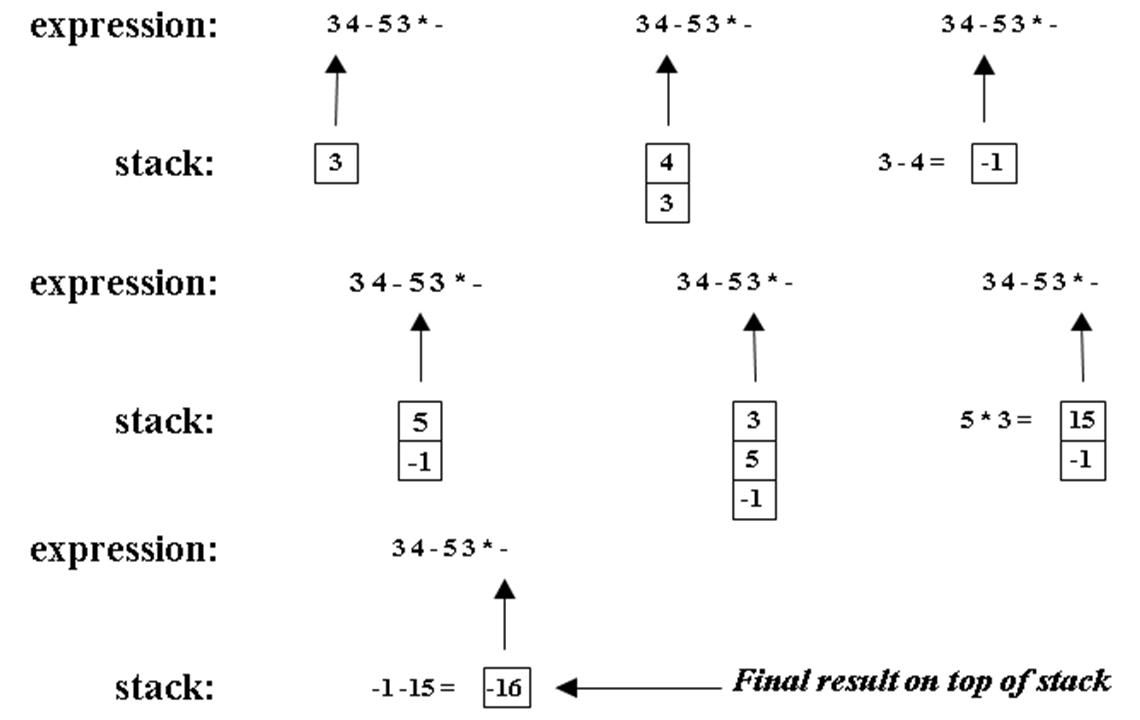
Sample expression

Let's see how the following infix expression would be written in RPN and evaluated using a stack:

(3-4)-(5*3) = -1 - 15 = -16

In RPN this would be written as:

3 4 – 5 3 * -

When a number is read in it is pushed to the stack. When an operator is read in, we check to see if there are number(s) available on the stack as operands for that operator. If so, those numbers are popped from the stack, the operation is evaluated and the result is pushed back to the stack.

Most computer programs involve the use of methods (in OO languages) or functions (in functional languages) that are called as the program runs. In this section we talk about methods, but everything applies also to functions.

Methods can be called from other methods. When one method calls another, execution switches from the code in the calling method to the code in the called method. When the called method completes, execution returns to the calling method.

It is important for the runtime environment to keep track of method calls so that the right code is executed at the right time. This is done by storing method calls and returning them in LIFO order – i.e. using a stack.

When a method is initiated, it gets its own copies of the parameters that are passed to it by the calling code.

Upon a method call, the data for the calling method, along with the address of where the call occurred, must be stored somewhere. These get stored on a stack data structure, the call stack, as ‘stack frames’ or ‘activation records’.

Recursion

A recursive call is a special case of a method or function call, where the code inside a method calls that same function again, which in turn calls the same function, and so on. While there is only one function involved, it may be called many times, and each call needs to be tracked by the call stack.

Method Stack in the JVM

The Java Virtual Machine (JVM) keeps track of the chain of active methods with a call stack

When a method is called, the JVM pushes onto the stack a frame containing

Local variables and return value

Program counter, keeping track of the statement being executed

When a method ends, its frame is popped from the stack and control is passed to the method on top of the stack. This allows for method calls including recursive calls.

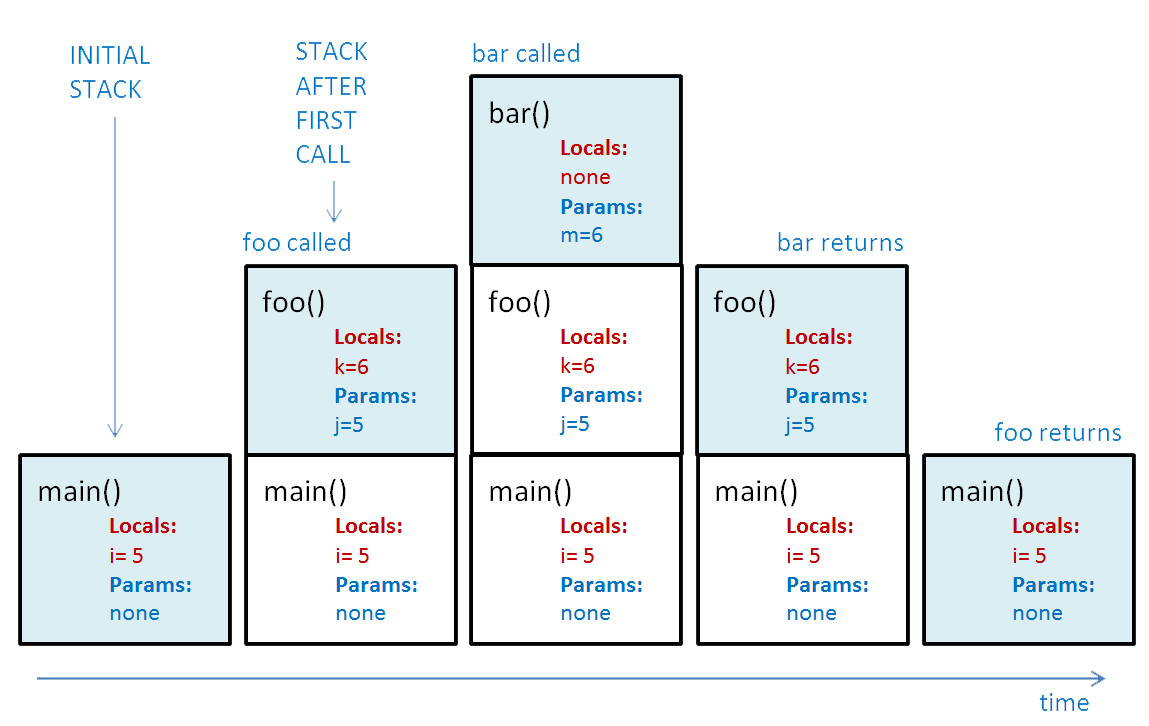
main() {
	int i = 5;
	foo(i);
}
foo(int j) {
	int k;
	k = j+1;
	bar(k);
}
bar(int m) {
	…
}

This diagram shows how the contents of the call stack change over time as methods are called. Time goes from left to right, and each stack of frames shows the contents of the call stack at a point in time.

Stack frames

A stack frame contains all that is necessary to restart a method:

The location of the next instructions

The values of all local variables

The values of all parameters

A call to method g from method f:

Loads a stack frame

Pushes the frame on to the ‘call stack’

Binds the formal parameters for g to the actual parameters for f

Transfers control to the first instruction in g.

To return to method f from g:

Pop the top stack frame from the call stack

Use the values in the stack frame to reinitialize the values for f

Bind the return value for the call to g

Transfer control to the return address in function f

Computes an integer power of a floating point number

double power(double base, int exponent) {
    if (exponent < 1) {
        return 1.0;
    } else {
        return power(base, exponent-1) * base;
    }
}

The function is called as follows:

System.out.println( power(1.7, 3) );

Initial bindings

base = 1.7

exponent = 3

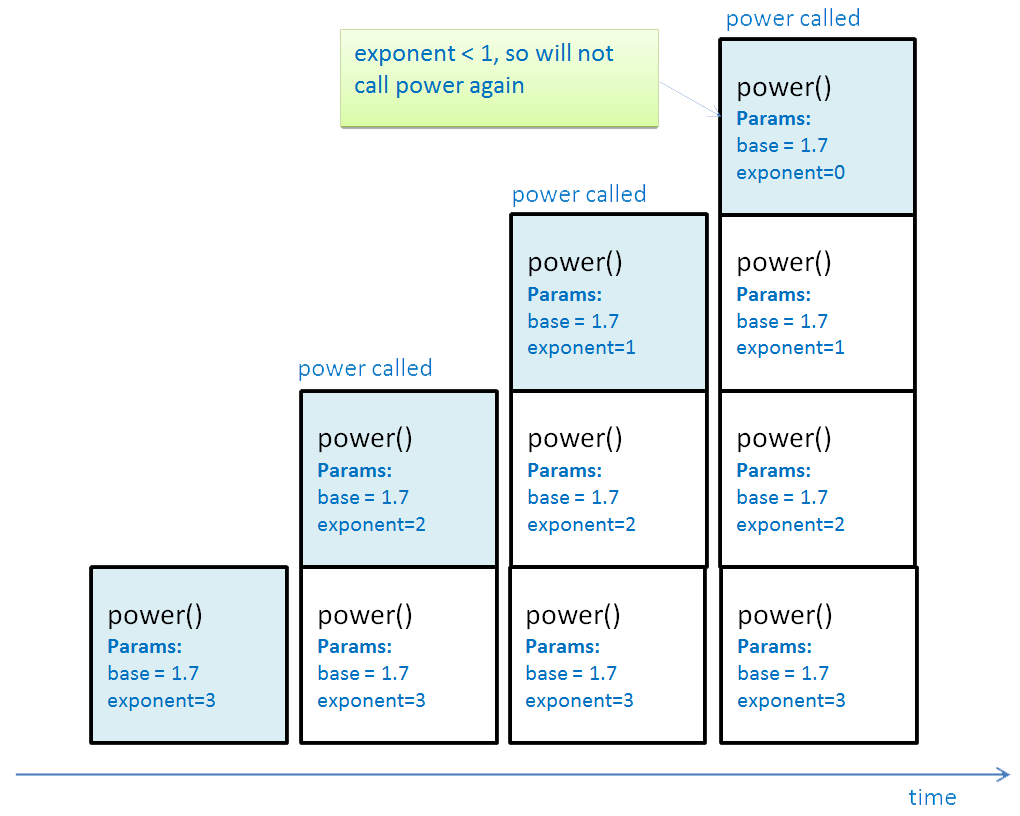
This diagram shows how the contents of the call stack change as recursive calls are made. Each time power executes, it makes another call to power, and pushes a new stack frame to the call stack. The value of the exponent parameter is different each time – look at the code to see why. At the fourth call, exponent is now < 1, so the other branch of the if statement executes and power is not called again. This is the stopping condition – without it the recursion would go on forever!

Call stack with recursive calls

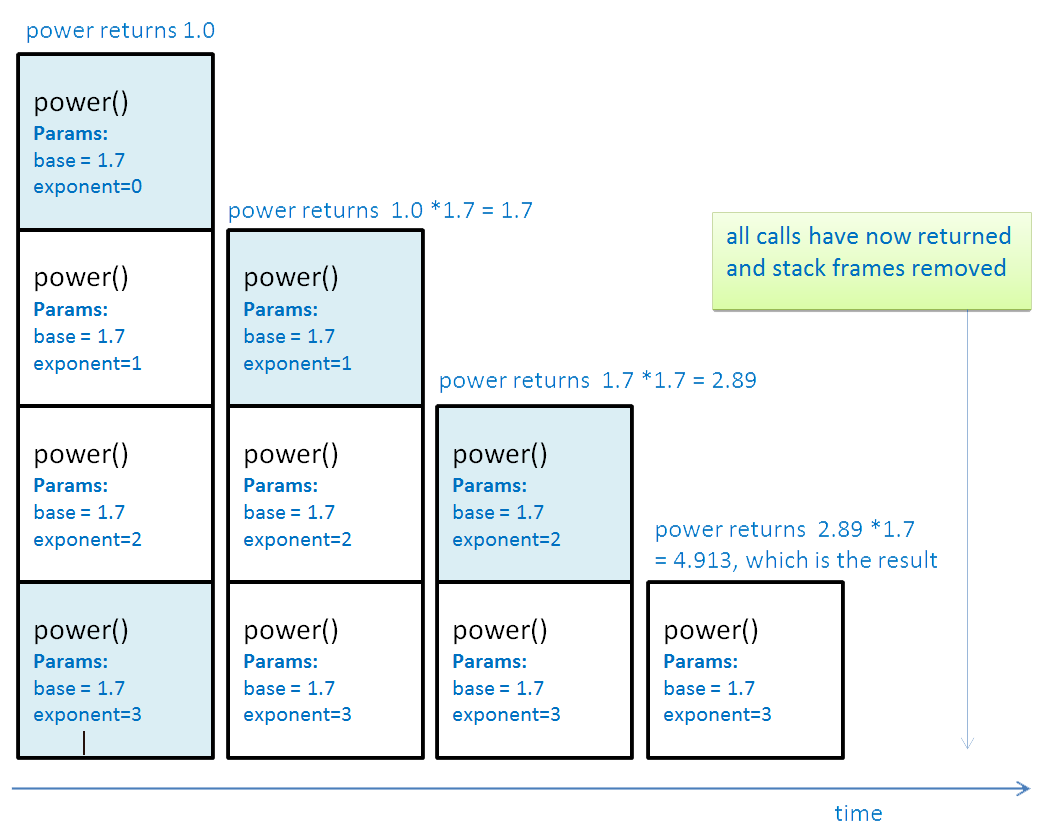
In the fourth call, power returns 1.0 and that frame is popped from the stack. Execution returns to the third call, which returns the result of calculating:

power(base, exponent-1) * base

which is:

value returned by fourth call * base

= 1.0 * 1.7

= 1.7

Now the third frame is popped from the stack and execution returns to the second call, which in turn returns the result of calculating:

value returned by third call * base

= 1.7 * 1.7

= 2.89

Now the second frame is popped from the stack and execution returns to the first call, which in turn returns the result of calculating:

value returned by second call * base

= 2.89 * 1.7

= 4.913

Each return does the following:

Pops a frame off of the stack

Restores its data state

Replaces the call to power with the return value

Continues execution at the return address

Call stack as recursive calls return

Recursion and RAM

Recursive functions may require more space in memory than non-recursive calls. With some deeply recursive algorithms this can be a problem. It is possible to run out of memory space on the stack – stack overflow.

It can also be a problem with poorly written recursive functions with bad stopping condition definitions (result is like an infinite loop only on the stack)

Advantages of recursion

Recursion’s big advantage is the elegance with which it embodies the solution to many problems

It closely follows the mathematical definition of many functions

This makes it easier to prove correctness

Some problems are much easier to solve recursively than iteratively, e.g. Towers of Hanoi

Disadvantages of recursion

Use of system resources slows the process down compared to iterative solutions, although this may not be a big factor on modern machines

Possibility of stack overflow

Difficult to ‘think recursively’

You have seen that a stack can be used to evaluate postfix expressions. However, when you write expressions in most programming languages, you don't write postfix. One of the jobs that a compiler typically does is to translate expressions to postfix notation so that they can be evaluated.

The compiler's job of translating code that you write into something that can be executed is helped by the presence of brackets, in expressions and elsewhere in the code, as well as other symbols – all those tedious { and }, ( and ) and so on. The compiler uses a stack when checking these. This example is a simple illustration of how this works.

Parentheses Matching using a stack

Each “(”, “{”, or “[” must be paired with a matching “)”, “}”, or “[”

For example:

    correct: ( )(( )){([( )])}
    correct: ((( )(( )){([( )])}))
    incorrect: )(( )){([( )])}
    incorrect: ({[ ])}
    incorrect: )(

Parenthesis Matching (Java Code)

The method isMatched takes a string and returns true if all the brackets match correctly, false otherwise. The expression could be a string containing the contents of a Java source file.

public boolean isMatched(String expression) {
    SimpleStack buffer = new SimpleStack();
    buffer.createStack();
    final String opening = "({["; // opening delimiters
    final String closing = ")}]"; // closing delimiters

    for (char c : expression.toCharArray()) {
        if (opening.indexOf(c) != -1) // this is a left delimiter
            buffer.push(Character.toString(c));
        else if (closing.indexOf(c) != -1) { // this is a right delimiter
            if (buffer.isEmpty()) // nothing to match with
                return false;
            if (closing.indexOf(c) != opening.indexOf(buffer.pop())) 
                return false; // mismatched delimiter
        }
    }

    return buffer.isEmpty(); // were all opening delimiters matched?
}

Note that this method makes use of the SimpleStack class we looked at earlier on. Alternatively we could have used a Java Collections Framework class such as the Stack. See the following link for documentation on that class:

🔗 https://docs.oracle.com/javase/9/docs/api/java/util/Stack.html