Introduction

A tree is a hierarchical structure with its data (nodes) arranged according to some ordering property.

Searching linearly in a list is O(n) and can be expensive for a large data collection. However a binary search for sorted collection is of the order O(log2 n) providing improved performance for large collections of data, for example, finding an item from billion items arranged in sorted order requires at most only 30 comparisons. Similarly, binary search tree (BST) organizes the data such that most operations are O(log2 n) on average.

This week we will:

Introduce the Tree ADT and its usefulness for solving problems

Learn about tree insertion and deletion strategies

Learn about tree traversals

Understand the difference between binary trees, binary search trees and general trees

Trees can have different types:

General trees – each node can have any number of children

Binary trees – each node has at most two children

Binary search tree (BST)– the values are ordered
Definitions

A tree is a collection of nodes.

the collection can be empty; otherwise,

it consists of a special node, called the root, and zero or more subtrees

Node - an element of a tree

Root node - first node in a tree structure

level - The root node is at level 0. The children of root node are at level 1 and so on.

Parent node - a node which is predecessor of another node.

Child node - A node which is a descendant of another node. A node can have only one parent and children of the same parent are called siblings.

Leaf - Nodes without children are called leaves or external nodes. Nodes that have one or more children are known as internal nodes.

Subtree - Every node of a tree is the root of a subtree.

An edge is a connection between two nodes

A path between two nodes is defined as a sequence of nodes from one node to the other.. The length of this path is the number of edges on the path.

Depth of a node is the length of the unique path from the root to that node. . Thus, the root is at depth 0.

Height of a node is the length of the longest path from that node to a leaf. Height of tree is equal to the height of the root node. All leaves are at height 0.

The depth of a tree is equal to the depth of the deepest leaf; this is always equal to the height of the tree.

Diagram of a tree structure is highly recursive. Therefore, as you would expect, the algorithms that manipulate trees are also recursive in nature.

ADT Operations

create(root) // add root node to tree isEmpty( ) // check for empty tree insert (root, node) // inserts new node delete (root, node) //remove a node traverse(root) // visit all nodes in tree retrieve(root, node) // returns pointer to a subtree search (root, node) //find a node

Binary Tree

A binary tree is an ordered tree with the following properties:

every node has at most two children

each child node is either a left child or a right child

a left child precedes a right child in the order of children nodes

A tree is ordered if there is some meaningful linear order among the children of each node.

An example of a binary tree (i.e. one in which each node has no more than two children)

This tree also has the property that each node is greater than either of its children.

Consider the hierarchical ordering for the following tree. In this tree, each node is greater than all of the nodes in its left subtree and less than all of the nodes in its right subtree. This is called its ordering property and defines a BST.

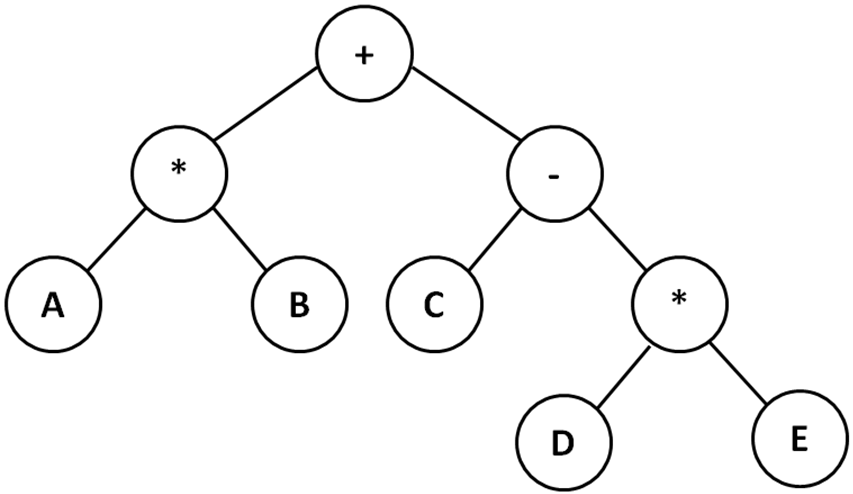
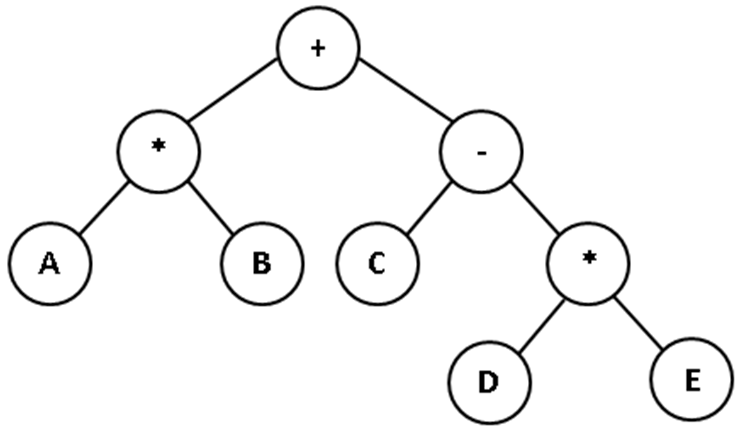
Trees representing arithmetic expressions

For example: (A*B)+(C-(D*E))

Reverse Polish Notation

Recall that expressions are easily evaluated using a stack if they are available in postfix form: AB*CDE*-+

Trees can be traversed in such a way as to produce the postfix form, e.g. a post order traversal yields the postfix form of the expression.

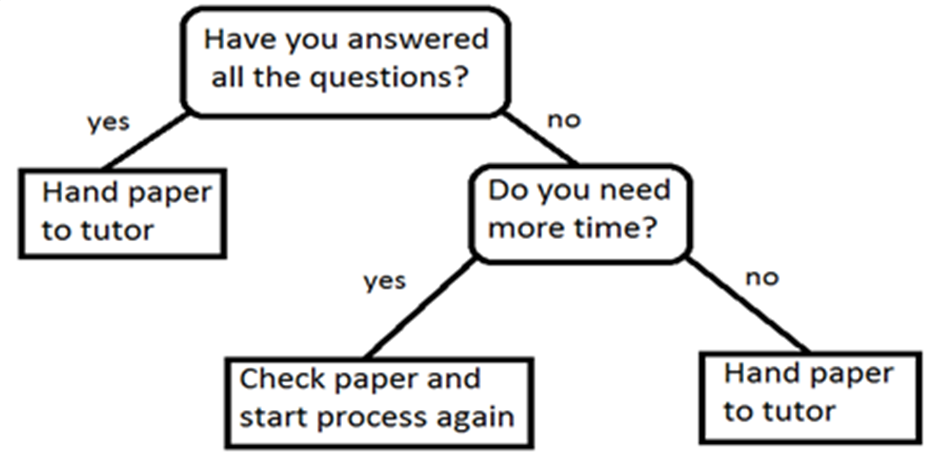
Decision trees

Decision trees can be used to represent a number of different outcomes that result from answering a series of yes-no questions

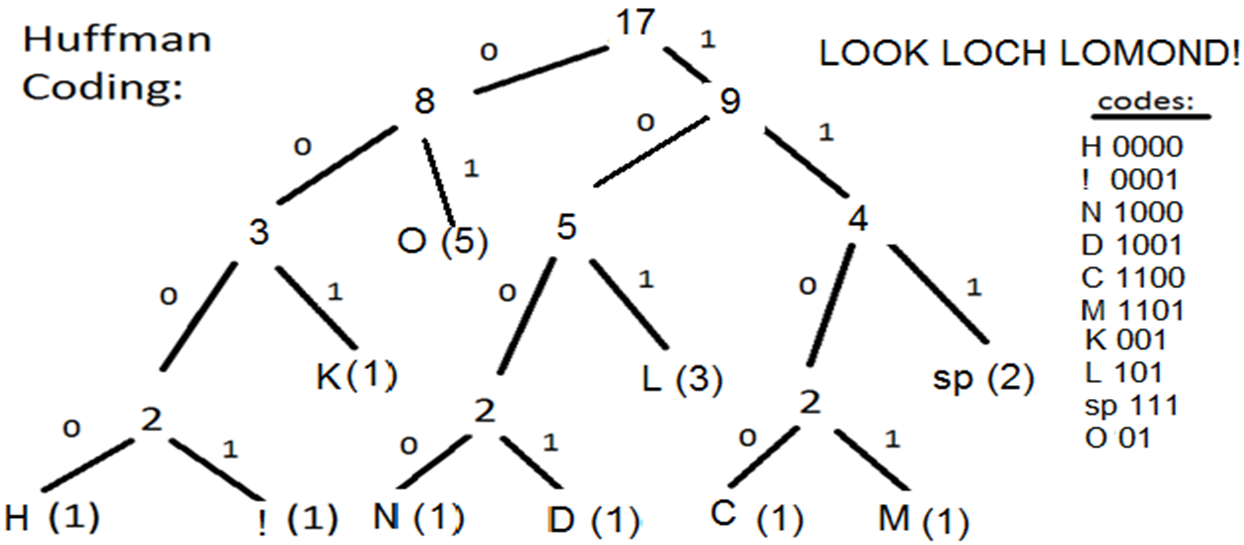
Huffman trees

Huffman codes compress data and are used in JPEG still image compression. A Huffman tree is a binary tree used to represent Huffman codes for text/characters that might appear in a message /file.

(For more details see Section 16.3, Introduction to Algorithms)

Binary Tree Representation

A binary tree could be represented using:
1. Linked representation
2. Arrays representation
Linked Representation
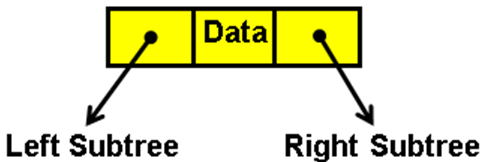
A tree node could be represented with a data and pointer fields for left and right subtree.
For example, consider the following tree
Tradeoffs
1. Faster updates (insertions and deletions are O(log2n) )
2. Extra memory for pointers
Array representation e.g. Depth (d)=3
1. Allocate an array of size 2(d + 1) -1
2. Store root in location 1
3. For node in location n,: store left child in location 2n,; right child in location 2n+1
Tradeoffs
1. Fast access (given a node, its children and parent can be found very quickly)
2. Slow updates (insertions and deletions require physical reordering)
3. Wasted space (partially filled trees)

Traversing Binary Tree

A tree traversal visits each node of a tree exactly once.

Modes of traversal

When visiting a node we have three choices

1. Process the data

2. Process nodes in the left subtree

3. Process nodes in the right subtree

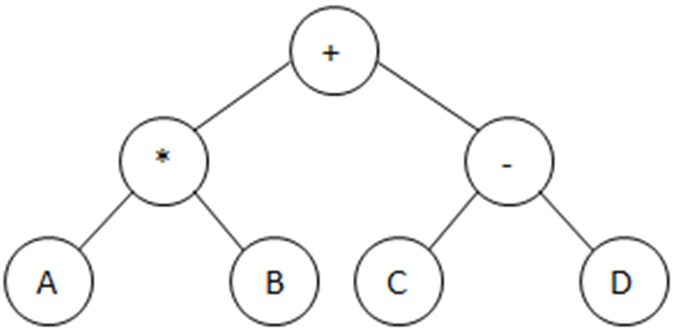
Example arithmetic expression tree

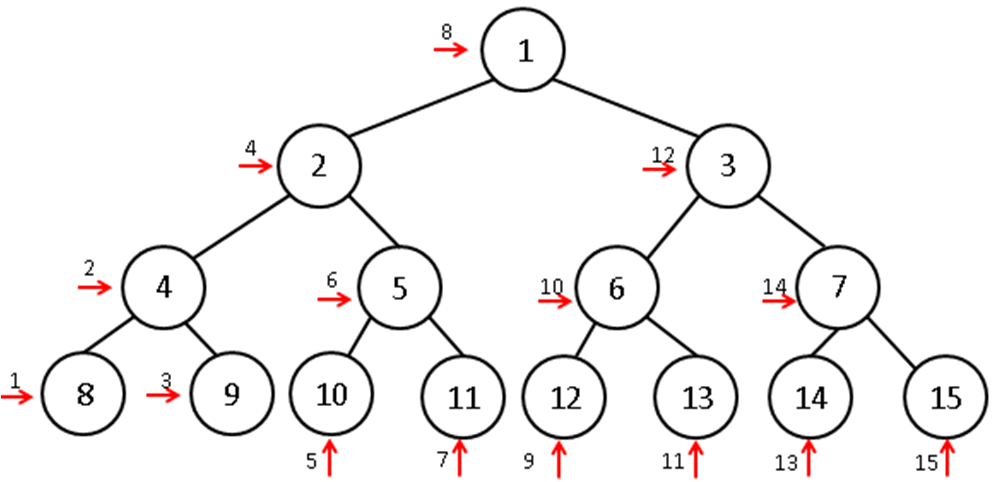
Steps for a Preorder traversal of a binary tree

1. Process root

2. Do a preorder traversal of the nodes in the root's left subtree (recursively)

3. Do a preorder traversal of the nodes in the root's right subtree (recursively)

In processing a node if we simply write out the data contained in the node, then a preorder traversal of tree T produces +*AB-CD

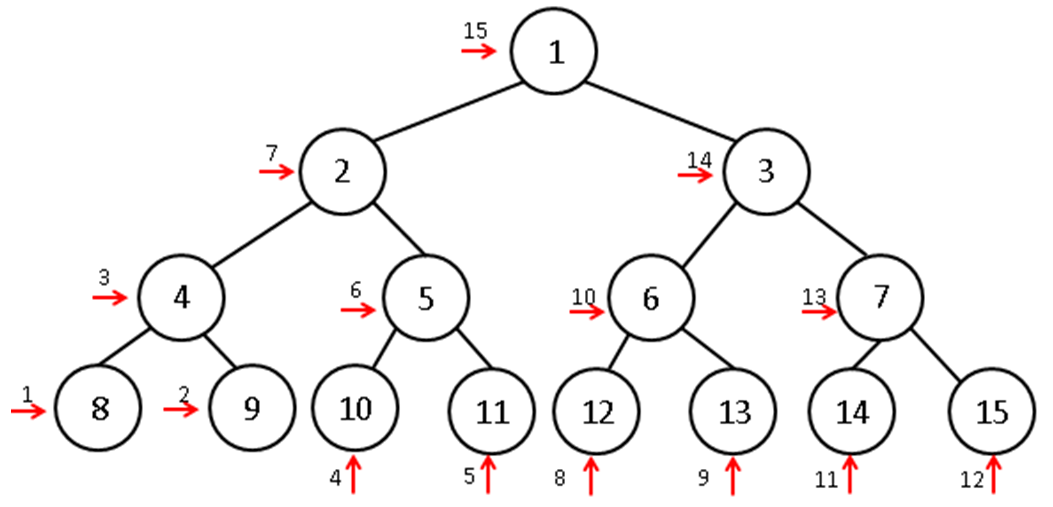
Steps for an Inorder traversal of a binary tree

1. Recursively visit left subtree

2. Process root

3. Recursively visit right sub-tree

An inorder traversal of T produces (A*B)+ (C-D) (the infix form)

Steps for a Postorder traversal of a binary tree

1. Recursively visit left subtree

2. Recursively visit right subtree

3. Process Root

A postorder traversal of T produces AB*CD-+ (the postfix form)

These traversals can be done on any binary tree, not just expression trees.
Inserting into a BST

In order to insert a new item, we first need to determine the appropriate location where the new item can be added while preserving the ordering property.

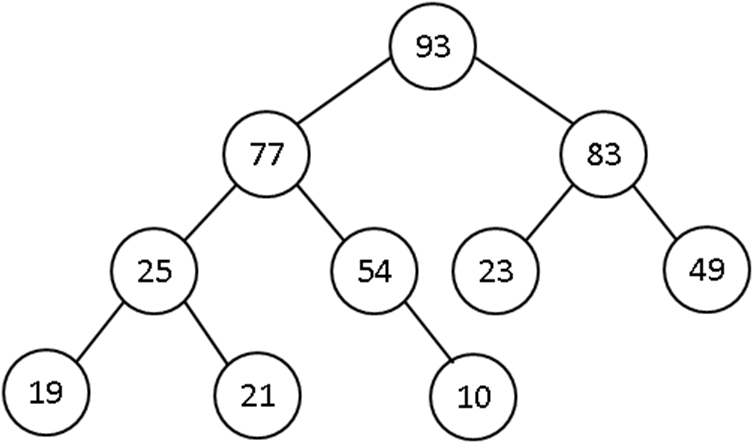
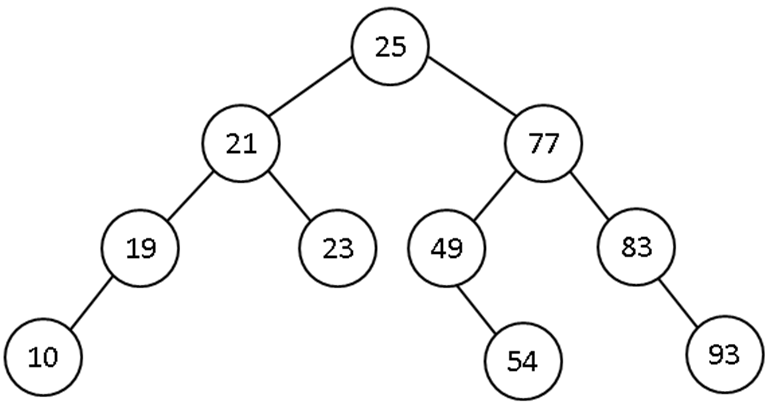
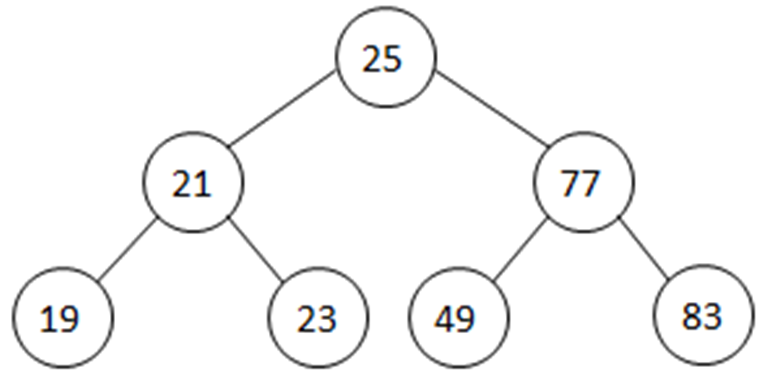
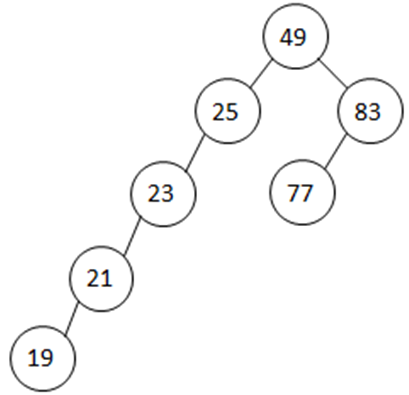
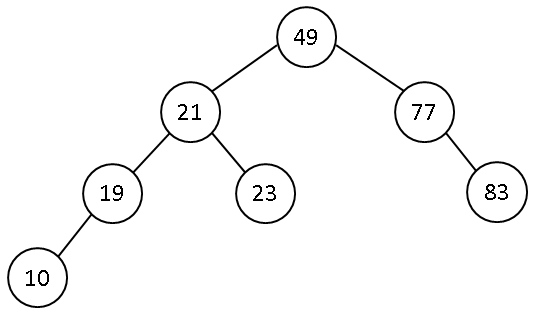
Consider the following tree

Inorder traversal of this tree gives 19, 21, 23, 25, 49, 77, 83, that is, the inorder traversal visits the nodes in ascending order.

To find the location to insert a new value, we start at root, and then either go left, if new value is less than root, otherwise go right.

Example: Adding 10 to the previous tree.

1. Compare 10 to 25 (the root).

Since 10 < 25, add 10 to the left subtree of 25

2. Compare 10 to 21 (the root of the left subtree).

Since 10 < 21, add 10 to the left subtree of 21

3. Compare 10 to 19.

Since 10 < 19, add 10 to the left subtree of 19

4. As the left subtree is NULL, add 10 at this location. Left pointer of 19 will point to this new node.

Efficiency of adding to a binary tree

The efficiency of adding a value to a binary tree is related to the depth of tree. A tree with only one node, that is, the root node is considered to have a depth 0. For the tree considered above, a total of 3 (depth + 1) comparisons were performed.

Clearly the number of comparisons is determined by the shape/depth of the tree.

Differing tree configurations

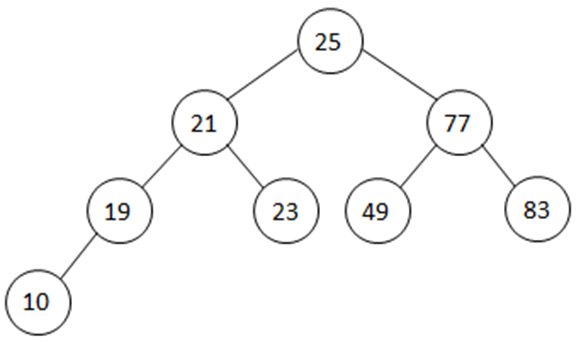
For example, consider the tree below containing the same data but in a different arrangement.

The number of comparisons to add 10 would be 5 (depth + 1)

If the tree is full, or balanced then the depth would be minimum and so would be the comparisons.

A tree of height h is a full tree if all leaves are at level h. A balanced binary tree is one in which every node above level depth-1 has exactly two children.
Deleting from a BST

Deleting from a tree

The tree after deletion must preserve the ordering property, i.e., it must remain a BST. Consider the following tree.

Deletion Strategies

There are three cases to be considered:

1. Node to be deleted has no children, that is, a leaf

2. Node to be deleted has either a left or right subtree

3. Node to be deleted has both a left and right subtree

Case 1: Node to be deleted has no children, that is, a leaf

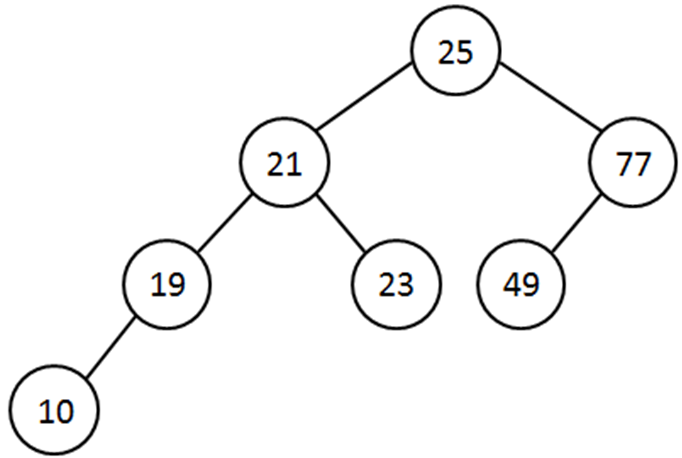
Example: deleting node 83

Set the right subtree of 77 to null. The resulting tree is given below.

Case 2: Node to be deleted has either a left or right subtree

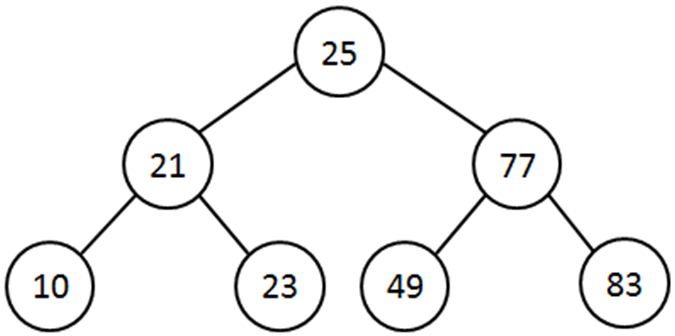
Example: deleting node 19

To delete 19, we replace 19 by its left subtree (node 10). The resulting tree is given below.

Case 3: Node to be deleted has both a left and right subtree

Example: deleting node 25

To delete 25, we find its inorder successor (49), that is, the smallest node in the right subtree and copy its value to node 25. This ensures that the ordering property is preserved. The resulting tree is given below.
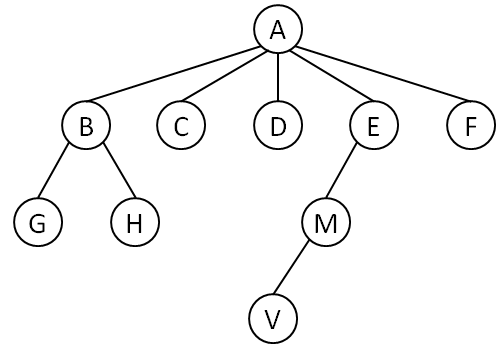
General Trees

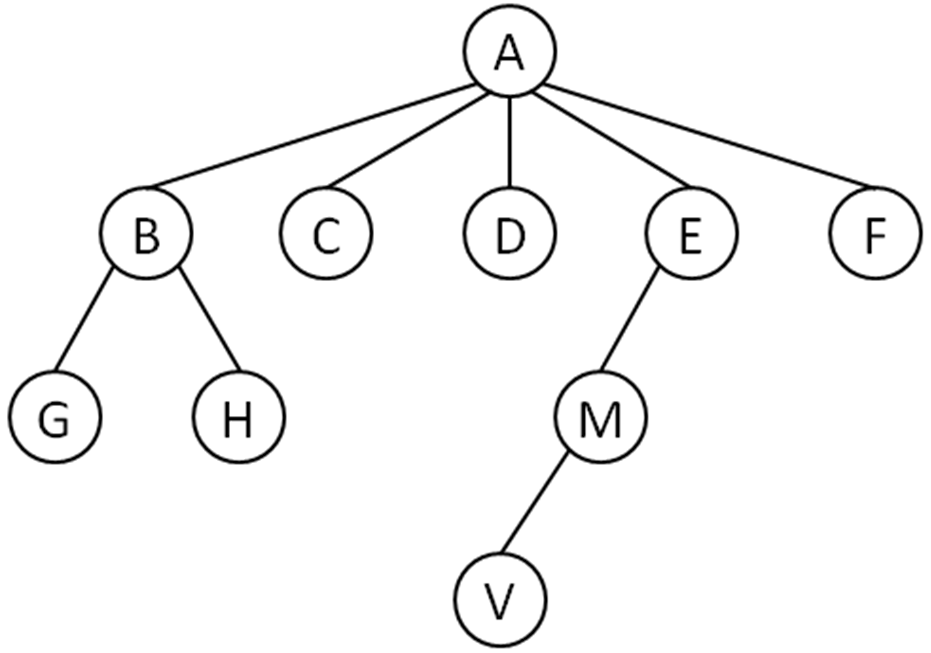
So far we have been studying binary trees, general trees however can have more than two children for each node.

If we convert a general tree to a binary tree then we can apply what we have learned for binary trees to it.

Converting a general tree to a binary tree

This could be achieved by:

1. Retain edge (connection) from a parent node to only its left-most child at next level

2. Insert an edge from left-most child (selected above) to connect all siblings from left to right at the same level

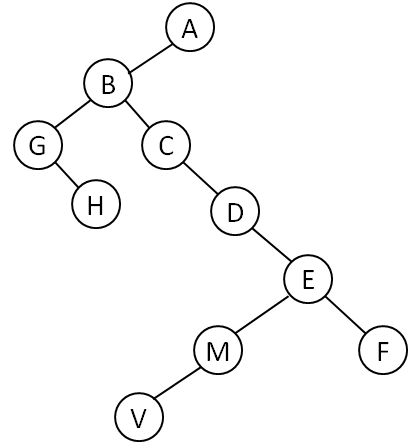
Imagine the nodes have a layout

Binary version of a general tree

The general tree shown above can be converted to the following binary version.

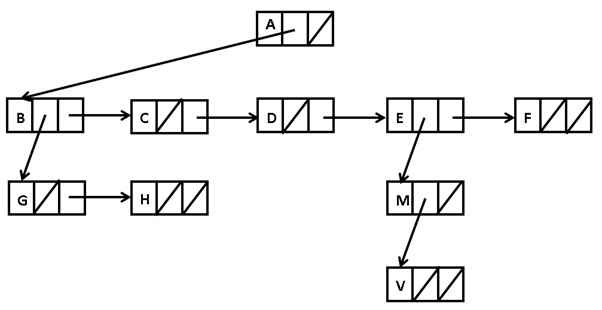
This can be represented as

Preorder Traversal

(Visit Root, Left, Right)

A B G H C D E M V F

Processing order

1. Process root

2. Recursively traverse the left-most subtree

3. Recursively traverse the next subtree to the right

4. Repeat step 3 until there are no more subtrees

Postorder Traversal

(Left, Right, Visit Root)

H, G, V, M, F, E, D, C, B, A

Inorder Traversal

(Left, Visit Root, Right)

This is left as an exercise.
Another Example of General Tree Traversal

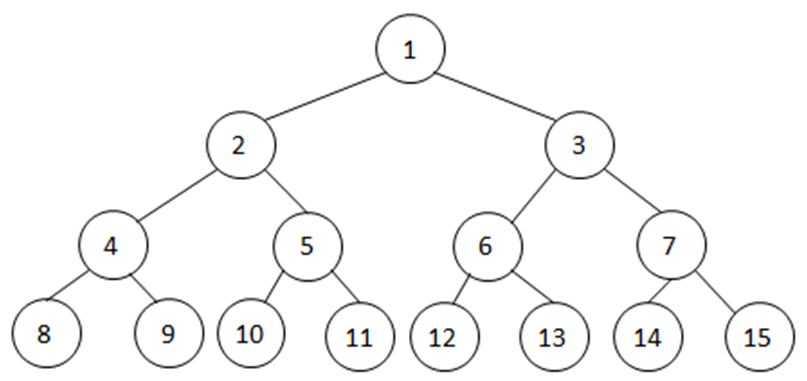
Sample tree to illustrate tree traversal

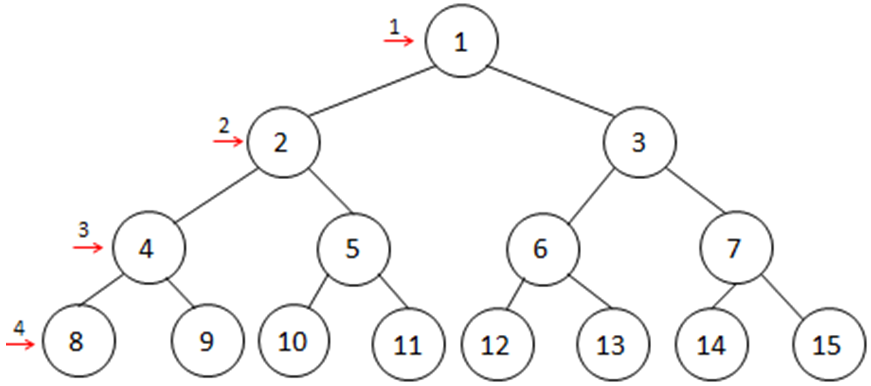
Tree after four nodes visited in preorder traversal

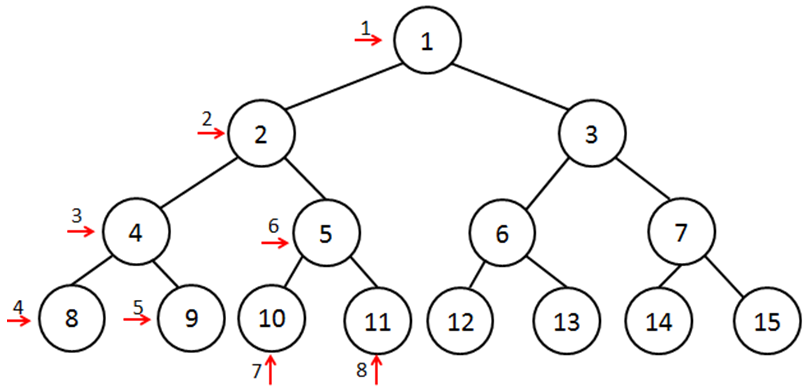
Tree after left subtree visited using preorder traversal

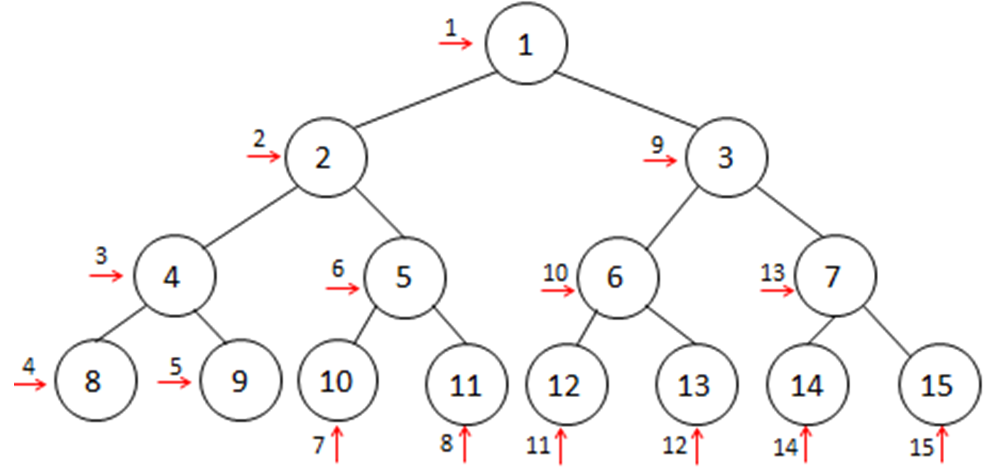
Tree after completed preorder traversal

Tree visited using inorder traversal

Tree visited using postorder traversal