• Introduction

    Binary search tree is an important type of tree. We have already seen how the different types of traversals and deletion operations can be performed. Finding a node location is an important first step for many of the other operations, such as insertion and deletion.

    The operations must obey the ordering property of the binary search tree (BST).

    In this week we will:
    Understand and apply the important operations on binary search trees
    Learn how to use recursive operations to process trees
    Consider other types of tree structures

  • Binary Search Tree (BST)

    A Binary Search Tree (BST)

    Binary Search Tree Example 1

    An ordered tree ADT
    BSTs are ordered structures and this allows for fast operations such as retrieval and insertion.
    Many searching and sorting algorithms are based on a strategy of divide and conquer.
    That is, a solution is found by breaking the problem into smaller (similar) sub problems. This process is often implemented using recursion.

    Definition of BST

    A Binary Search Tree (BST) is either
    1. An empty tree, or
    2. A tree consisting of a node, called the root, and two children called left and right subtree, each of which is also a BST. The value at each node is greater than the left subtree values and less than the right subtree values.

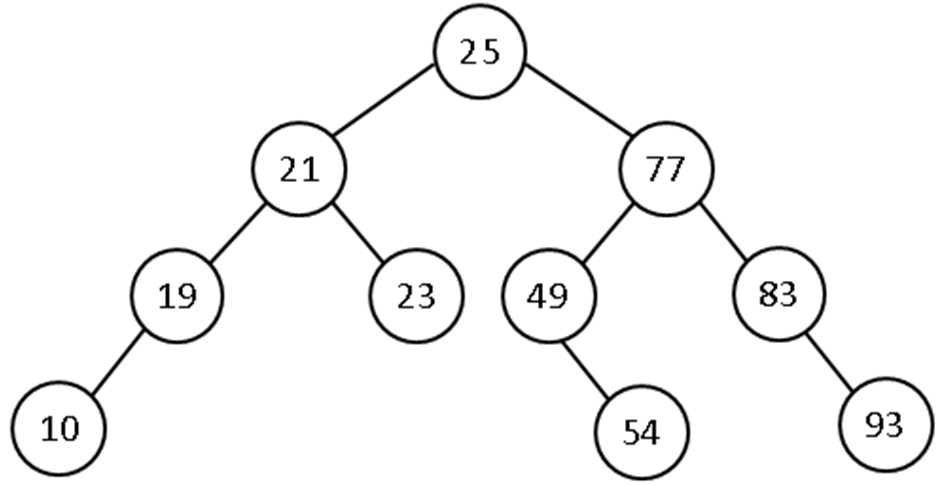
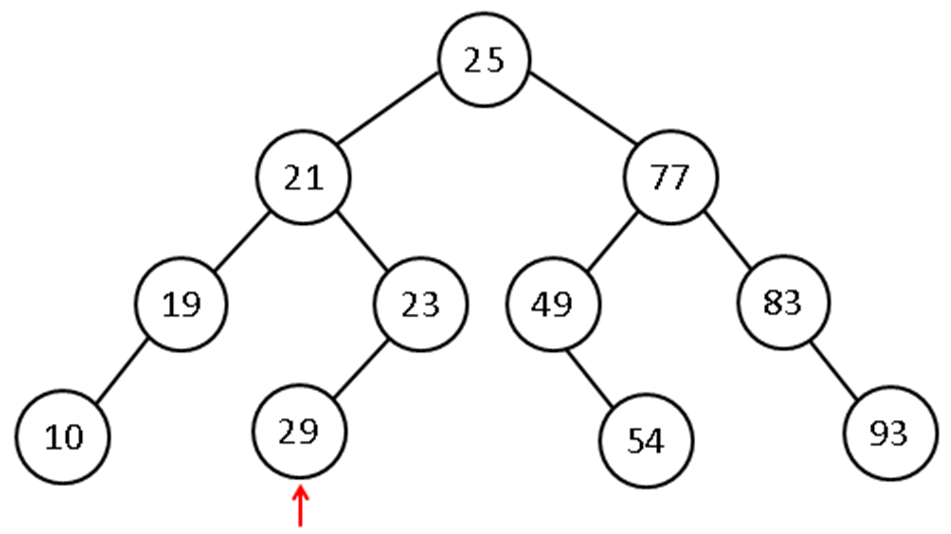
    The addition of a value to a BST must preserve the ordering property and must hold true for each node in the tree. For example, in the tree below, node 29 violates the BST property.

    Where can it be inserted for the tree to remain a BST?

    Definition of Binary Search Tree Example

    Adding a value to BST

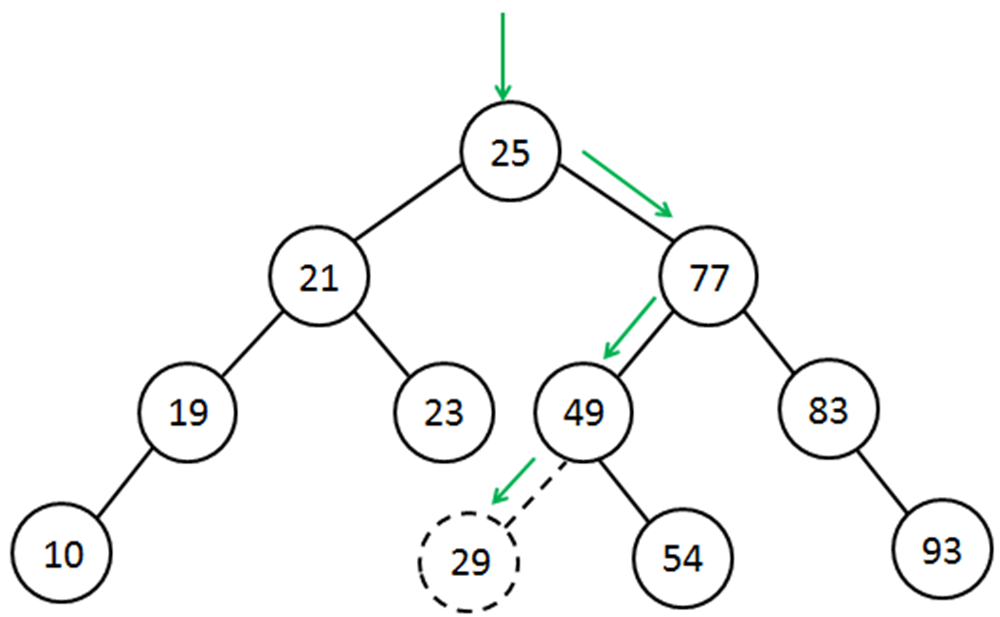
    Adding Value to Binary Search Tree Example

    Before a value is added to a BST its appropriate location according to the data ordering property must be determined. Adding value 29 will comprise of following steps.

    1. Starting at the root, compare 29 to 25
    As 29 > 25, proceed right
    2. Compare 29 to 77
    As 29 < 77, proceed left
    3. Compare 29 to 49
    As 29 < 49, proceed left
    4. As left subtree of node 49 is empty, so 29 can be added as left subtree of 49.

  • Binary Search Tree ADT

    A Binary Search Tree ADT stores its data by following the definition of BST.

    BST ADT Operations

    Create( )		// create an empty tree
isEmpty( )		// check for empty BST
insert( )		// insert a node
remove( )		// delete the specified node
retrieve( )		// search for a value
traverse( )		//visit each node and process

  • Binary Node Class Definition

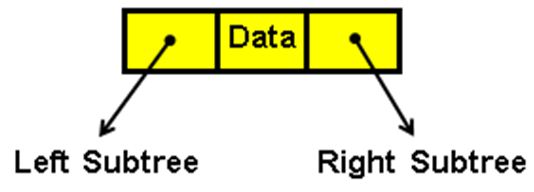
    A binary tree node contains:
    Data
    Pointer to Left Subtree
    Pointer to Right Subtree

    Binary Node Definition Example 1 

    class TNode {
    private int item;
    private TNode lptr;
    private TNode rptr;
    
    TNode(int data)
    {
        item = data;
        lptr = null;
        rptr = null;
    }
}

    BSTree representation

    In the following tree representation, the null values for left and right subtrees have been represented as
    BSTree representation Example 1

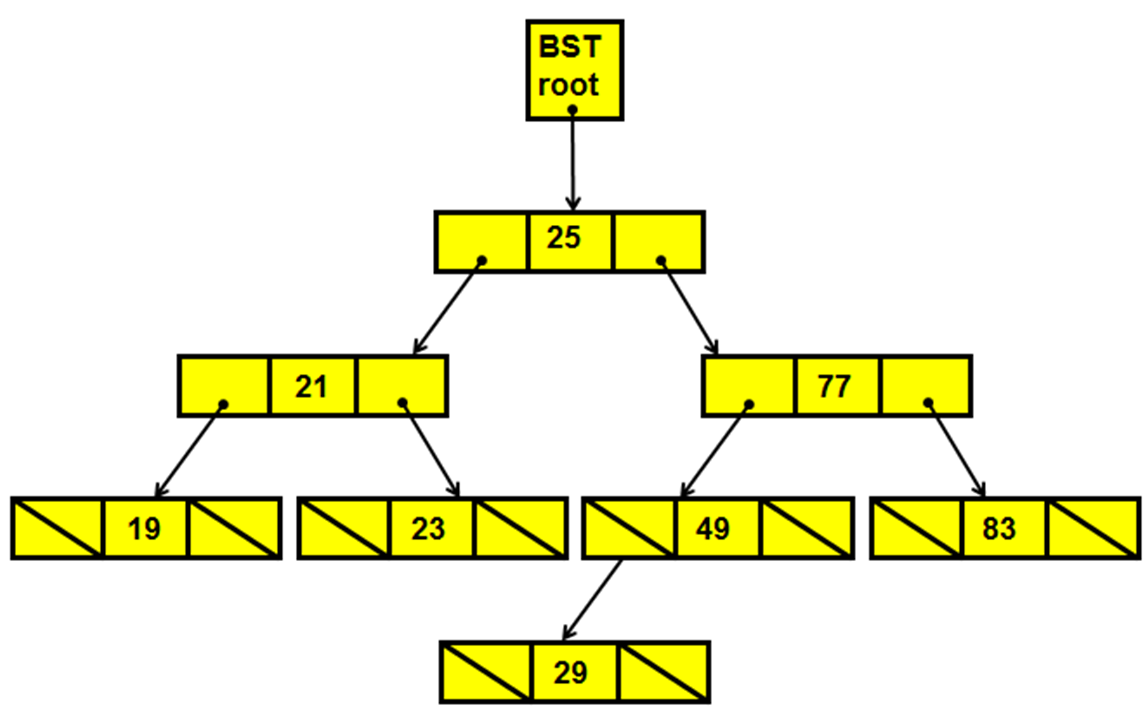
    BSTree Representation full diagram

  • BST Implementation

    public class BSTree {
   private TNode root = null;
}

constructor

BSTree( ) {
   root = null;
}

isEmpty
public boolean isEmpty( ) {
   // check for empty BST
   return ( root == null );
}

traversal

    It is useful to have a public method that does not require the client code to know about the root member. This public method could then call a private method of the class. This also applies to other methods requiring access to root member.

    Also note that the traversal visits each node and in this method we are only printing the value but any other processing could be applied.

    public void inOrder()
{
    inOrder(root);
}

private void inOrder(TNode rootptr)
{
    if (rootptr != null)
    {
        inOrder(rootptr.lptr);
        System.out.println(rootptr.item);
        inOrder(rootptr.rptr);
    }
}


insert

public void insert(int item)
{
   root = insert(root, item); 
}


private TNode insert(TNode rootptr, int item)
{
    if(rootptr == null)         //empty tree
    {
        rootptr = new TNode(item);
        rootptr.item = item;
    }
    else
        if(item < rootptr.item) //go left
            rootptr.lptr = insert(rootptr.lptr, item);
    else                        //go right
            rootptr.rptr = insert(rootptr.rptr, item);   
    return rootptr;               

}

    The implementations of retrieve and remove are similar and are left as lab exercise.

    Creating a BST

    public static void main(String[] args) {
    BSTree bst = new BSTree();
    bst.insert(25);bst.insert(21);
    bst.insert(77);bst.insert(19);
    bst.insert(23);bst.insert(49);
    bst.insert(83);bst.insert(10);
    bst.insert(54);bst.insert(93);
      	
    }
}

    The resulting BST

    Binary Search Tree Implementation Example 1

    Note that the values have been inserted in preorder to build this tree. An inorder traversal would access the values in sorted order, that is, 10, 19, 21, 23, 25, 49, 54, 77, 83, 93.

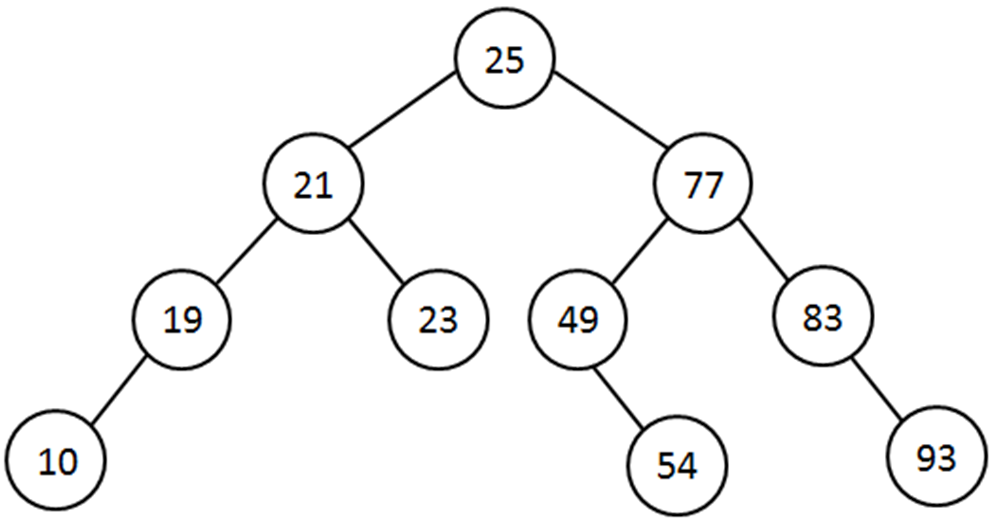
  • Efficiency of Tree Operations

    We have seen earlier that the shape of a tree determines the efficiency of tree operations.

    An efficient tree (full and complete) is shown below.

    Efficiency ofBinary Search Tree Operations Example 1

    The maximum number of nodes can be determined as.

    $$ f(d) = 2^{(d+1)}-1 $$

    The number of nodes in a full tree can be obtained as shown in the table below. If a binary tree of N nodes is balanced, no branch will be longer than log(base 2)N+1. Thus, the efficiency of the insertion algorithm would be O(log2 N).


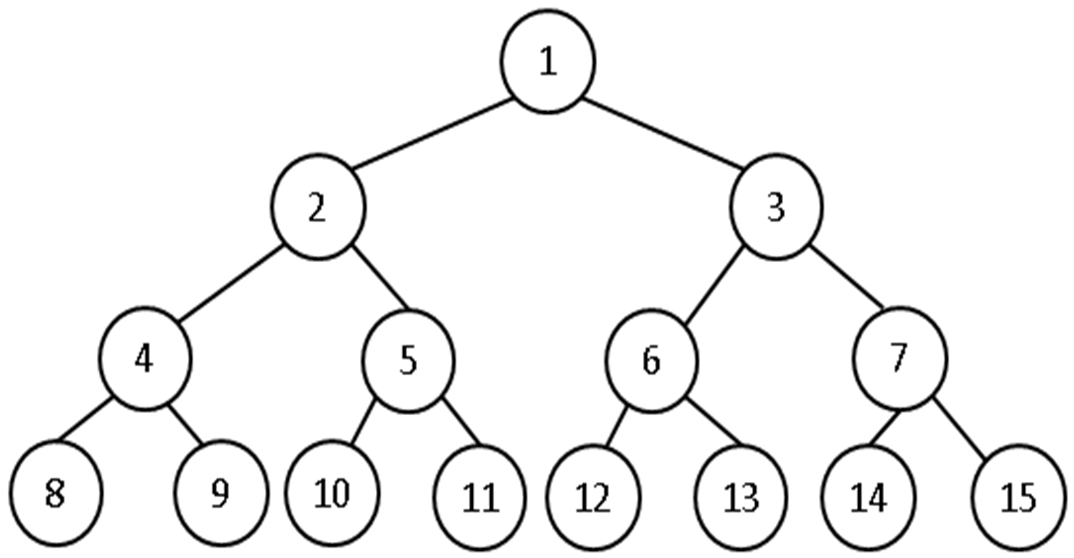
    Depth (level) of tree Nodes at the depth (level) Max nodes in tree
    $$ f(d) = 2^{(d+1)}-1 $$
    0 20 = 1 1
    1 21 = 2 3
    2 22 = 4 7
    3 23 = 8 15
    4 24 = 16 31
    ... ... ...
    10 210 = 1024 2047

  • Tree Sort

    Tree sort is a sorting algorithm that is based on BST. If we build a BST with the values to be sorted and then traverse the BST using inorder traversal, we will obtain the values in the sorted order.

    Inserting n values into a balanced BST is O(n log2 n) where each value would be O(log2 N). Tree sort is thus very fast.

    However, the worst case occurs if the values to be inserted are already sorted as then the tree shape would be like a linked list.

  • Other Tree Types

    Trees are extremely useful data structures and the following types address some of the problems encountered with the basic tree structures.

    AVL trees
    The first self-balancing tree data structure to be put together is the AVL tree named after Adelson-Velsky and Landis
    They are not perfectly balanced but pairs of sub-trees differ in height by at most 1

    Splay tree
    A splay tree is a self-adjusting binary search tree with the additional property that recently accessed elements are quick to access again.
    It performs basic operations such as insertion, look-up and removal in O(log n) time.
    For many sequences of non-random operations, splay trees perform better than other search trees, even when the specific pattern of the sequence is unknown.

    Red–black tree
    A red–black tree is a kind of self-balancing binary search tree.
    Each node of the binary tree has an extra bit, and that bit is often interpreted as the colour (red or black) of the node.
    These colour bits are used to ensure the tree remains approximately balanced during insertions and deletions

  • Chapter Summary

    Trees are non-linear structures representing data in a hierarchical manner.
    General trees can have any number of nodes whereas binary trees can have a maximum of two nodes as children.
    The ordering in a Binary Tree, left child is processed before right.
    The data in a tree can be visited using in-order, pre-order, and post-order traversals.
    The Binary Search Tree is an ordered tree ADT. The insertion anddeletion operations must preserve the BST property.
    The performance of Binary Search Tree can degrade for unbalanced trees.
    Treesort can sort a list using a Binary Search Tree.