Week 10: Sets, Maps and Tables

Introduction

Sets contain an unordered collection of elements modelling the mathematical set. Maps make it possible to associate a key to another set of values. Hash tables are implementations of map structure. We have already seen search strategies for different data structures and the best ones with O(log2 n) are binary search (the data must be ordered) and a Binary search tree (the tree must be balanced). The question is can we do better than this?

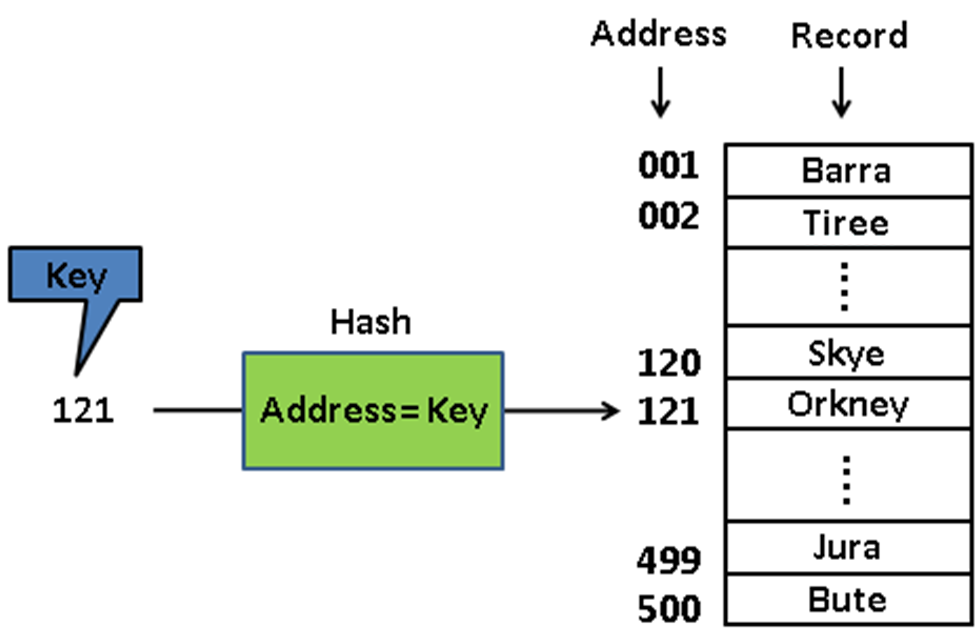
Consider storing a value k at array location k. In such a case, searching for a value k could use the array index directly. Such an operation is O(1) irrespective of the size of the array. In hashing, we map a given key to its corresponding array index location enabling search for an item in O(1).

This week we will:

Look at the Java Set and Map interfaces and how to use them

Learn about hash coding and its use to facilitate efficient insertion, removal, and search

Look at different forms of collision strategies for hash tables—open addressing and chaining—and to consider their relative benefits and performance trade-offs
The Set Interface
A set is an unordered collection of elements containing no duplicates. Duplicates are however allowed for a multiset (bag).

Java.util.Set interface is defined in Java Collections Framework
(🔗 https://docs.oracle.com/javase/9/docs/api/java/util/Set.html) and defines the following methods:

boolean add(E obj) – adds the specified element to this set if not already present

boolean addAll(Collection c) -Adds all of the elements in the specified collection to this set if they're not already present

boolean contains (Object o) - Returns true if this set contains the specified element

boolean equals(Object o) - Compares the specified object with this set for equality

boolean isEmpty() - Returns true if this set contains no elements

boolean remove(Object o) - Removes the specified element from this set if it is present

boolean removeAll(Collection c) - Removes from this set all of its elements that are contained in the specified collection

int size( ) - Returns the number of elements in this set (its cardinality)

In addition the fundamental set operations are also defined in the Java Set interface

For two sets A = {10, 20, 30} and B = {2, 4, 6, 8, 10},

The Union of the two sets A and B includes the elements that are in set A, B, or both and is represented as,

A U B = {2, 4, 6, 8, 10, 20, 30}

The intersection of the two sets A and B includes only the elements that are in both A and B and is represented as,

A ∩ B = {10}

The difference of the two sets A and B contains all the elements which are in A but not in B.

A-B = {20, 30}, similarly B – A = {2, 4, 6, 8}

📷 addAll( ) method

📷 removeAll() method
```
Set<String> codes = new HashSet<>();
codes.add("alpha");
codes.add("beta");
codes.add("zeta");
codes.add("gamma");
                
System.out.println(codes); //prints [zeta, alpha, beta, gamma]
System.out.println(codes.size()); //prints 4
System.out.println(codes.contains("beta")); //prints true
         
Iterator<String> iterator = codes.iterator();
while (iterator.hasNext()) {
      String name = iterator.next();
      System.out.println(name);
}
```
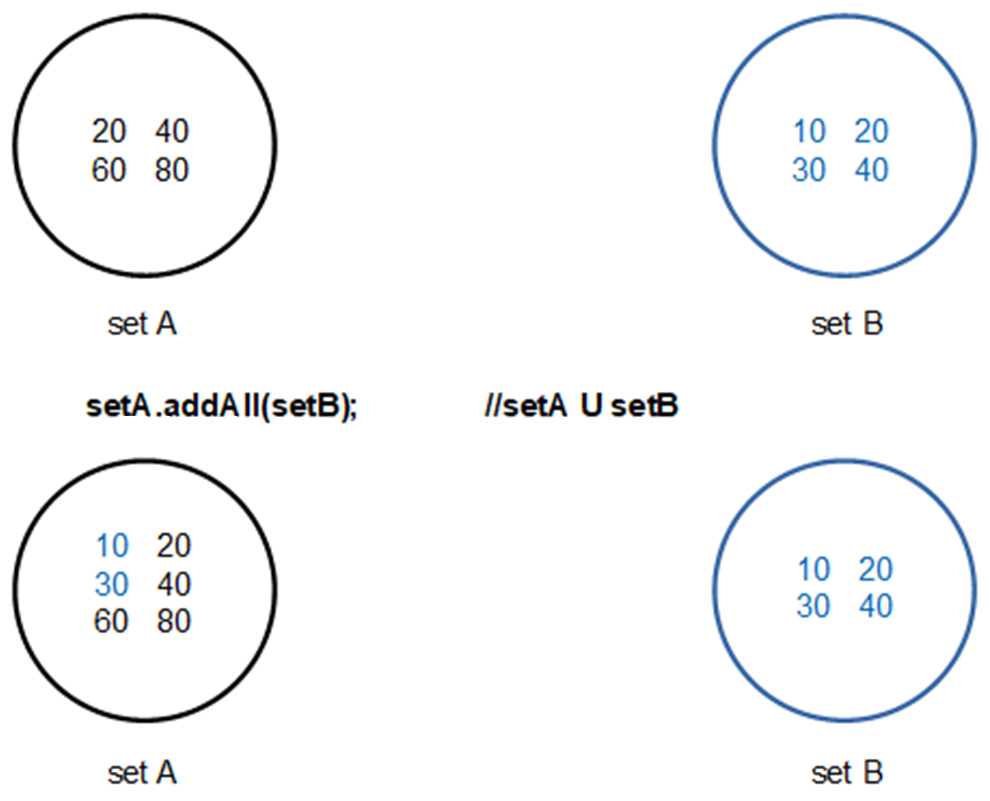X

X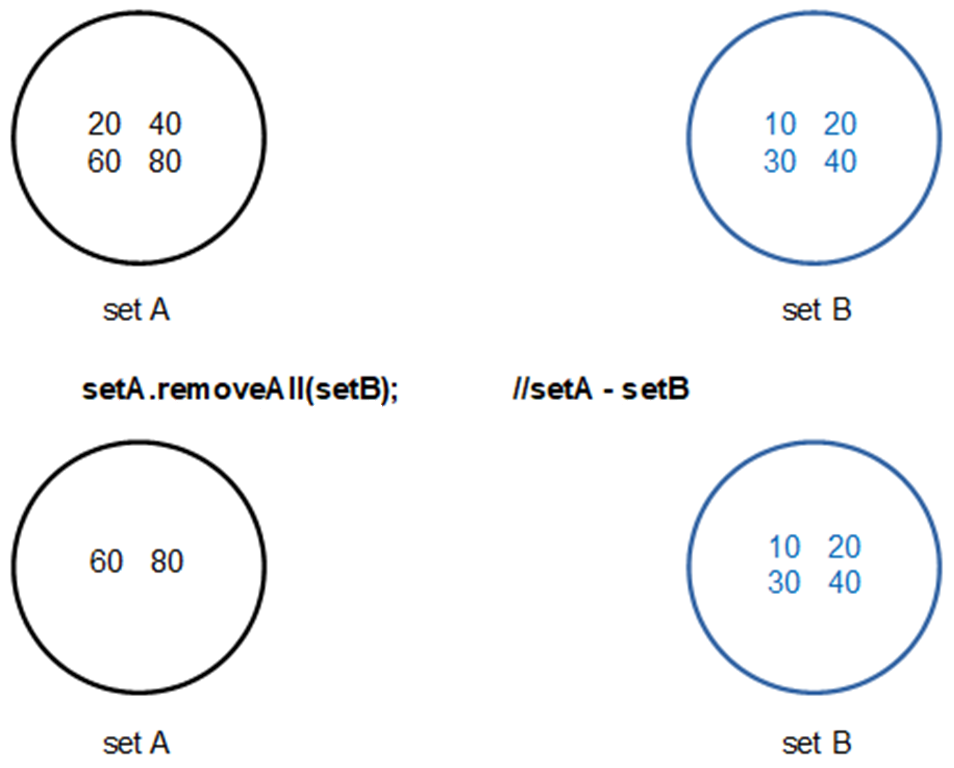
Maps and The Map Interface
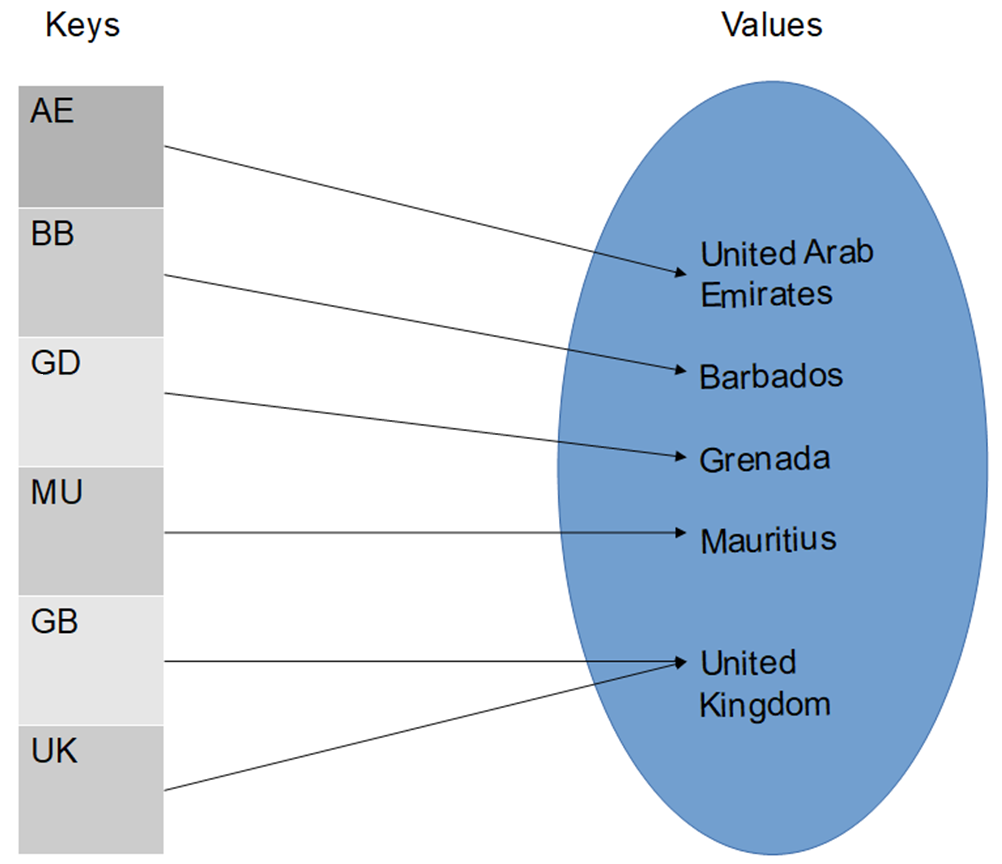
Map is a set of ordered pairs containing a key and a value. Map provides quick storage and retrieval of the values using the key.

A key provides a mapping from a keySet to a valueSet. The keys must be unique but valueSet may have duplicates, that is, more than one key could map to the same value. The stored value could be an aggregate item, for example, a keySet could contain the student ID whereas the valueSet could contain all the information about the student, such as, student name, email address, subjects enrolled, etc.

Map is implemented using hashing and is also known as a dictionary or an associative array.

The key is used to uniquely identify an element in the valueSet. All the elements of valueSet have a corresponding member in keyset.

A map can have many-to-one mapping, for example, in the figure above, both GB and UK map to United Kingdom.

Map interface should have methods of the form

V.put (K key, V value)

Map Interface

The following statements build a Map object with both the keys and values of type String:
```
Map<String, String> myMap = new HashMap< >();
        myMap.put("AE", "United Arab Emirates");
        myMap.put("BB", "Barbados");
        myMap.put("GD", "Grenada");
        myMap.put("MU", "Mauritius");
        myMap.put("GB", "United Kingdom");
        myMap.put("UK", "United Kingdom");

        System.out.println(myMap.get("GB")); //prints United Kingdom
        myMap.remove("AE"); //removes United Arab Emirates
```
Hashing - Direct Addressing

The fastest search solutions

The only way we can get O(1) efficiency in searching for Key in an array A is if either

1. Direct Access: Key is the position (index) of the data in array A: A[key]

2. Mapping: There is a key-to-address transformation of ‘key’ (hashing function) into the index: A[hash(key)]

Direct access

Direct access is often impractical because it requires keys to be in the range 0..array_size-1. More often, key data is to be accessed by names, social security number, etc. and thus, a hashing function (a key-to-address transformation) is required for most data sets.

Problems of ‘direct hashing’

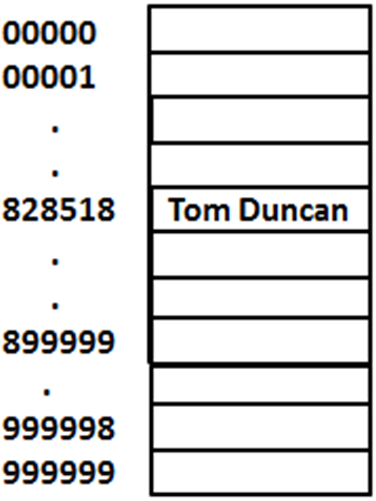
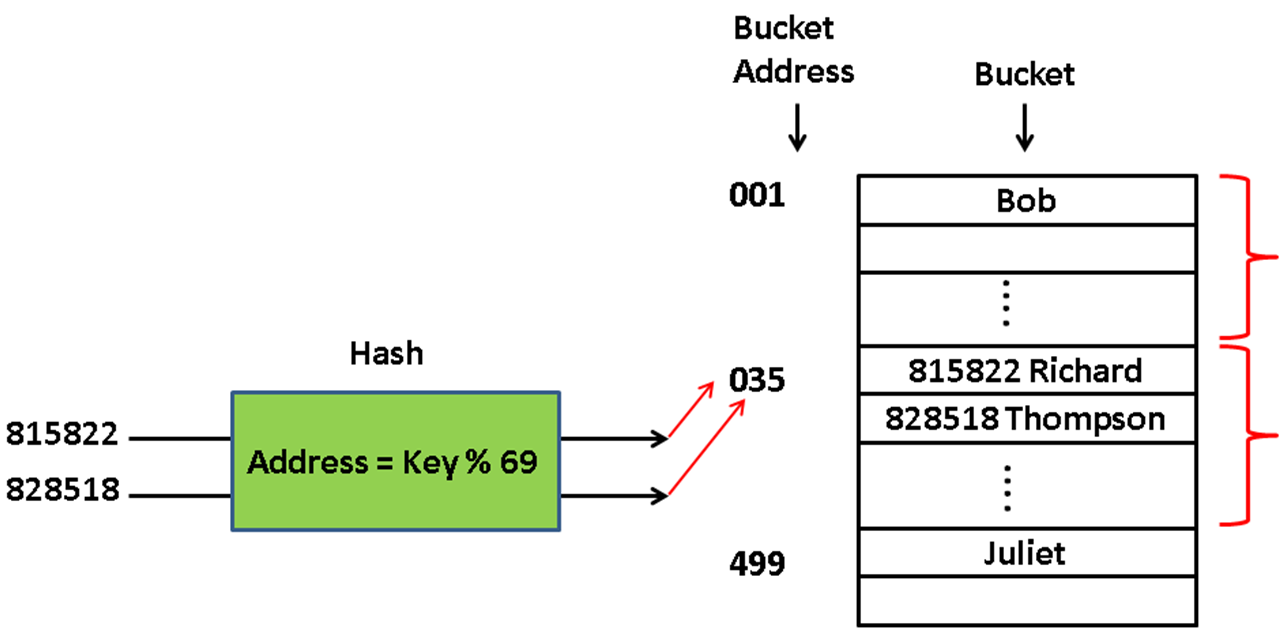
Imagine your company stores data for their employees by the key Employee ID (EmpID).

Suppose these numbers are 6 digits long in the format xx-xx-xx.

You would need an array of size 1, 000, 000 to hold all the possibilities from 00-00-00 to 99-99-99

Storing Employee IDs

To look up the information for an employee with number 82-85-18 you go directly to A[828518]

Advantages:

Direct lookup

Every employee has their own unique spot in the array

Disadvantages:

You only ever use a small portion of the array.

The rest of the space is wasted (and there is a lot of it)!
Hashing - Function Mapping
A better solution would map all the employees into a data structure without wasting a lot of space.

From the domain of all possible Emp IDs we want a structure that will store just the range of ones applying to our employees.

To do this we may have to convert the Emp IDs to something else.

📷 Hash function map

An example of hash conversion

Suppose we have student IDs in a range from 16000 to 16999 and that we intend to store these using hashing.
```
final int MAXSIZE = 16000;
```
A simple hash function to map the above range of values
```
hashKey = studentID – MAXSIZE ;
```
This gives us a number between 0 and 999.

We can use this unique number to directly access the array element containing data for that student.

Product code hash example

Student ID: 16121

Student: Zeta

Hashkey = 16121-16000 = 121

Another implementation

Student ID: 16121

Student: Zeta

Hashkey = 16121%16000 = 121

Digit Extraction Hashing

Selected digits are extracted from the key to create an address. For example, a number such as 82-85-18, can be used to create a 4-digit address by picking first, third, fifth and sixth digit to create 8818.

Folding

This technique uses the parts of a non-numeric field

82-85-18 becomes

82 + 85 + 18 = 185

This could further be randomized by the random number generator

Character to numeric key

Character strings can be converted to int by manipulating their ASCII codes:

“Jones”

J = 74

o = 111

n = 110

e = 101

s = 115

Hash key = 1177

Hashing in Java

Java directly supports hashing as every Object is equipped with instance method:
```
hashCode( )
```
X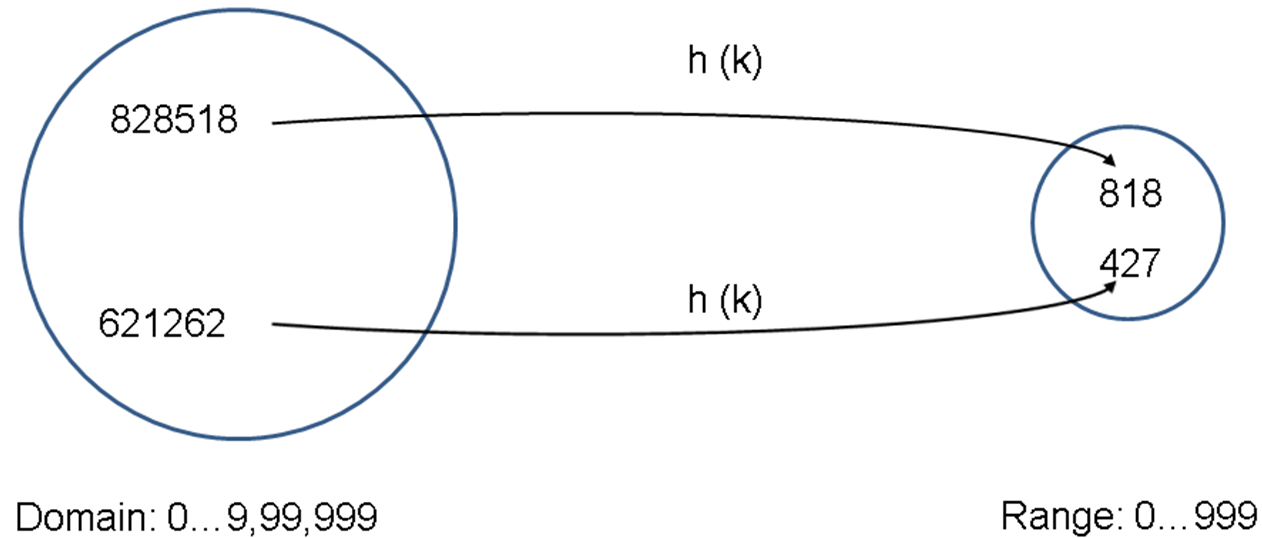

X
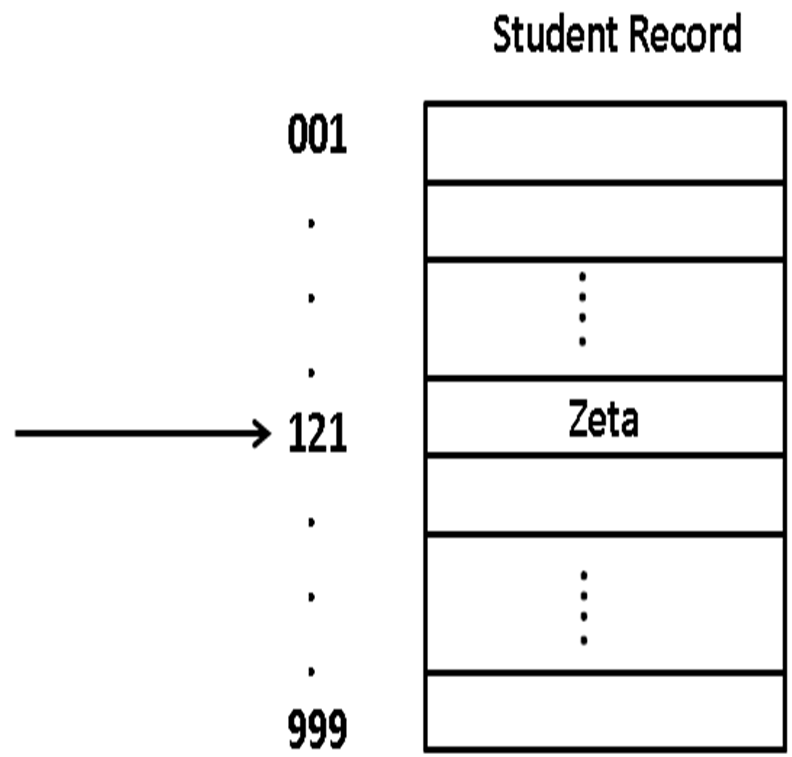
Collisions and hash Functions

Collision

Because there are many keys for each address, there is a possibility that more than one key will hash to the same address.

Collision – a hashing algorithm produces an address for an insertion key, and that address is already occupied.

Each hash should generate a unique number. If two different items produce the same hash code we have a collision in the data structure.

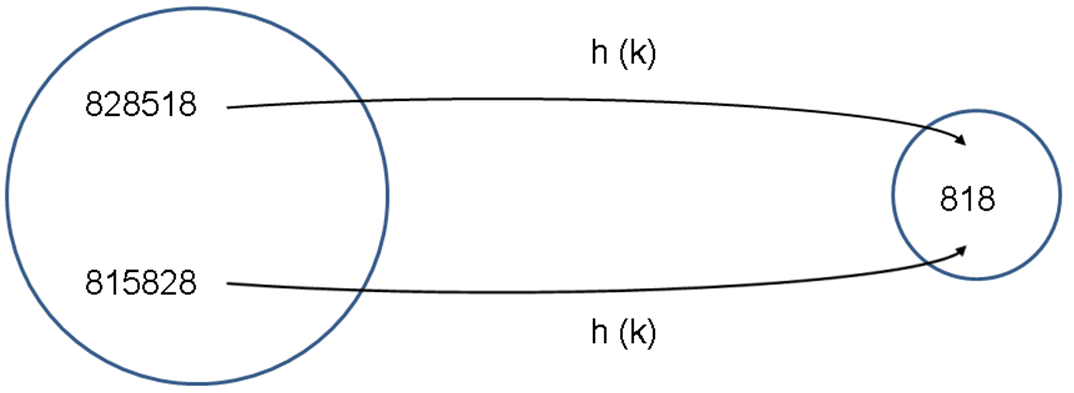
A Collision

Consider the case in the figure below with both numbers 828518 and 815828 being mapped to the same address 818 thereby resulting in a collision.

Two issues must be addressed

1. Hash functions must attempt to minimize collisions (there are strategies to do this).

2. If (when) collisions do occur, we must know how to handle them.

Two good rules to follow

A good hashing function must:

1. Always produce the same address for a given key, and

2. For two different keys, the probability of producing the same address must be low.

Picking good hash functions

We want one that spreads out the values evenly (random distribution) across a domain

If all the values cluster together

We have more collisions

We waste space in the rest of the data structure

A bad hash function. Why?

$$ h(k) = int \Big(\frac{k}{10,000}\Big) $$

An employee ID 45-67-32 is turned into a value of 456732. Applying the above function we get a value 45.

Thus, all IDs in the company could be mapped into an array of 100 elements (0 to 99). This is good, but could lead to problems?

The problem is...

Employees are likely to have the first two digits commonly the same if these were sequentially assigned.

This would cause lots of collisions

At best, it causes clustering

A rule for hash functions

“a good hash function depends on the entire key, rather than just a part.”

It is best if we use all the digits rather than throwing some of them away with integer division.

A better approach would divide by a prime number and take the remainder, to thoroughly mix the digits.
Collision Resolution Strategies

The collisions are bound to occur and so there must be strategies in place to cater for it. The two common ways in which it can be addressed is as follows:

Open Addressing

The main idea in these methods is to look for an available location in case of collision in the hash table. Several collision methods are available to attempt to resolve the problem:

Linear probing

Quadratic probing

Re-hashing

Chained Hashing

In case of collision, Instead of finding an open location we store the collided element at the same location. This is made possible by making available multiple storage locations corresponding to an index value.

Linked list resolution

Bucket hashing resolution
Collision Resolution-Linear Probing

No matter how good a hash function is, collisions will occur

With linear probing, when you hash into the table and find the spot already occupied, you go forward, in linear search fashion until you find a slot that has not been taken.

Then insert the item there.

Consider the hash table as shown with a hash function as k % 11.

📷 Collision

A collision occurs for adding 1916 (1916 % 11 = 2).

Location 2 is occupied so we probe further from location 2 linearly.

As location 3 is also occupied, so 1916 gets added

to the first free slot, that is, location 4.

📷 Wrapping around

The next problem we face however is what we do when a value maps into the last item in the table and it is already taken.

The solution is to wrap our linear search around to the beginning of the table and start from there.

A collision occurs for adding 1946 (1946 % 11 = 10).

Therefore we wrap around to location 0, and add

1946 at location 1.

📷 Deletions

The next concern we have involves deletions.

If we physically remove an item from the table there could be a problem that a search using linear probing could be prematurely terminated.

For example, we have seen that both 1960 and 1916 had mapped to location 2. Finding 1916 depends on the linear probe to start at location 2. If we delete 1960 then the search for 1916 will be prematurely terminated resulting in a failure.

📷 Deletion problem

For this implementation, we cannot delete items as long as linear probing is used to both store and lookup other items.

There are ways to mark records as ‘deleted’ without actually removing them from the array by adding another field to the structure of the array elements.

Lowering the likelihood of collisions

One easy method to lower the collision rate is to increase the size of the structure.

But how much larger should it be?

One rule of thumb is to make the structure twice as large as the number of elements you anticipate storing there.

Clustering

This problem may occur due to a quality inherent in your hash function, or due to the nature of the data itself.

If you notice it, you can alter the hash function.

The use of mod (%)

Mod is not a powerful enough hash operation to avoid collisions all the time.

To lower the possibility of collision we must intentionally waste space.

And, we must develop some strategy to deal with the collisions that inevitably occur.

Performance

Finally, we also have the issue of performance.

Direct access is O(1)

Structures (like the full employee ID array) that have ample space to avoid collisions have a O(1)…but they waste lots of space in memory and on disk if the structures are too big to fit in memory!

Structures that are compact and do not waste space in memory however, cannot usually provide O(1) lookup performance.

This is because of the frequency of collisions and the use of linear probing.

Linear probing is O(n).

This slows down overall lookup speed and takes us back to sequential searching – not good.

A balancing act

The best lookup tables are those that avoid collisions and yet minimize storage space.

This is a delicate balancing act that demands efficient hashing strategies.

One example of a situation to be avoided is clustering.

Random spread is best.

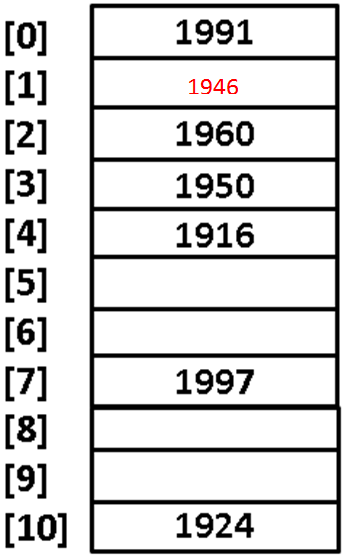X

X

X

X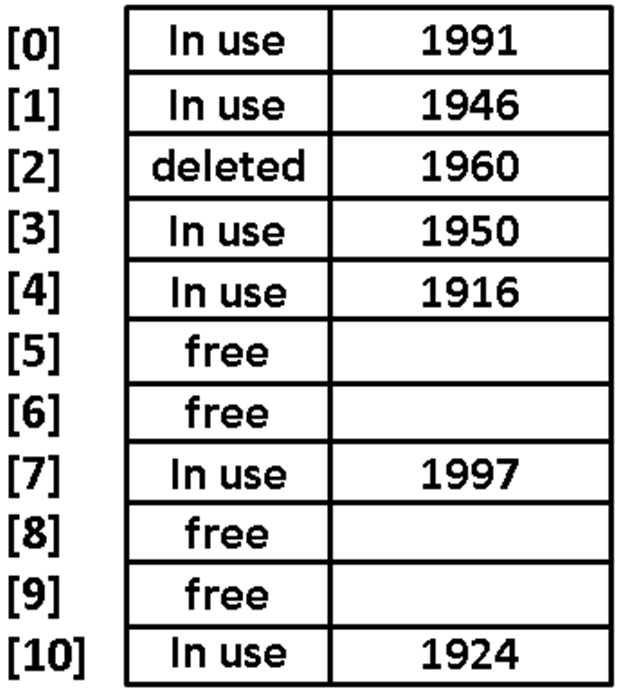
Collision Resolution-Quadratic Probing

In case of quadratic probing, if the slot is already occupied, then the next slot is found by following a probe sequence as.

A[loc], A[loc +1], A[ loc + 22], A[loc + 32] and so on until an empty slot is found.

Quadratic probing has the same issues as discussed under linear probing, that is, wrapping around, deletions, and clustering. However, Quadratic probing reduces the clustering problem.

Clustering problem

Assume that cells 4,5 and 0 are full.

If a new value hashes onto element 4

it then goes to:

Loc+1 = 5

Loc+4 = 0

Loc+9 = 5

Loc+16 = 4

Loc+25 = 5

Loc+36 = 0

Loc+49 = 5, etc!

Here we have a situation where the table is not full and yet there is no space to insert the next item!

Avoiding Quadratic Collisions

The solution is to use a list with a prime length.

Assume that cells 4,5 and 0 are full.

If a new value hashes onto element 4

it then goes to:

Loc+1 = 5

Loc+4 = 1 // this is open

Loc+9 = 6 // so is this one
Collision Resolution-Multiple Hashing

Multiple Hashing

An alternative approach to collision management is to apply a second hashing function if the first one results in a collision.

The aim is to produce a new hash address that will avoid a collision.

The second hashing function is generally used to place records in an overflow area.

Of course you still have the potential problems of finding the relevant records in the main structure or in the overflow area!

Re-hashing

Linear

try A[Addr], A[Addr+1], A[Addr+2], A[Addr+3], etc.

Quadratic

try A[Addr],A[Addr+1], A[Addr+4], A[Addr+9], etc.

Rehashing

try A[Hash1(Key)], A[Hash2(Key)], A[Hash3(Key)], A[Hash4(Key)], etc.
Collision Resolution-Chained Hashing

The basic idea is that instead of finding an empty slot to place an item in case of collision we store all the elements at the same address but in additional consecutive locations. This is made possible by storing the elements using linked lists or buckets.

While searching we follow the key to the required address location and can then search linearly for the required value.

This scheme simplifies the probing as in open addressing. However, the disadvantage in the use of extra space for storing pointers or buckets.

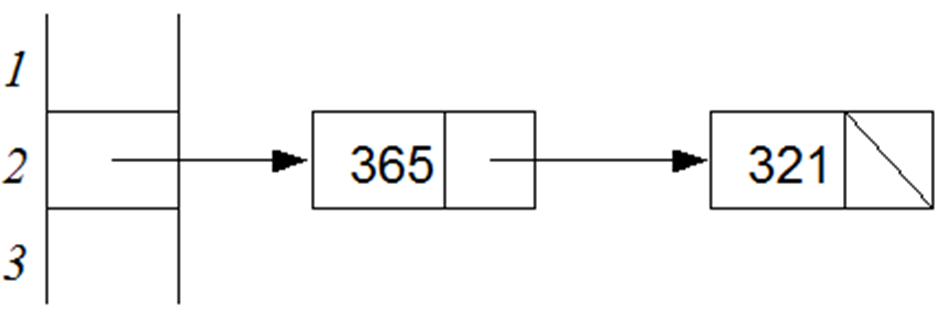
Bucket hashing resolution

Bucket – a node that can accommodate more than one record.

Closed-bucket Hash Table: Each bucket is separate from all others.
Summary

The Table ADT supports insertion and retrieval via a key.

A straight forward implementation of the table as an array doesn’t provide better performance.

Hashing can be used to build tables supporting rapid search, insertion and retrieval.

Collisions results when two keys resolve to the same hash address.

For collision resolution, chaining is an alternative to probing.

Introduction

The Set Interface

Maps and The Map Interface

Hashing - Direct Addressing

Hashing - Function Mapping

Collisions and hash Functions

Collision Resolution Strategies

Collision Resolution-Linear Probing

Collision Resolution-Quadratic Probing

Collision Resolution-Multiple Hashing

Collision Resolution-Chained Hashing

Summary