-
1. Introduction
This unit provides an introduction to vectors. We begin by defining what is meant by the term vector and describe how we distinguish vectors from scalars. The main properties of vectors are presented and the concept of a position vector is introduced. We then look at operations on vectors such as addition, subtraction and scalar multiplication both algebraically and graphically. The idea of a unit vector is introduced and we look at how to express the position vector of a point, in two and three dimensions, in Cartesian components using the standard unit vectors in the directions of the coordinate axes. The unit closes with a look at how to calculate the scalar (dot) product of two vectors.
-
2. What is a vector?
If required further resources on this topic can be found at:
📹 Intro to vectors and scalars
In our day to day lives we encounter many physical quantities such as time, temperature, weight, force, volume, velocity, acceleration and so on. Generally speaking we can separate these quantities into two groups known as scalars and vectors. Quantities that can be completely described by their magnitude (size) using a single real number, with appropriate units, are called scalars. For example, the temperature of an object is a scalar quantity when it is expressed by a numerical value alone in, say, degrees Centigrade.
Other quantities however need both a magnitude and direction for them to be defined fully and they are called vectors. A force acting on a body, for example, is a vector quantity as it needs both its magnitude, e.g. 30 Newtons and the direction in which it acts, e.g. downwards, to be specified.
A point to note here is that when expressed only as a numerical value temperature is a scalar but if we measure whether the temperature is increasing or decreasing it becomes a vector quantity as a directional component has been introduced.
A SCALAR is a quantity having magnitude but no direction.
Examples of Scalars
mass
energy
temperature
length
area
volume
density
pressure
speed
time
power
entropyA VECTOR is a quantity having both magnitude and direction.
Examples of Vectors
displacement
velocity
acceleration
force
weight
momentum -
3. Properties of vectors
Watch this video up to 5:40:
📹 Vector notation (2D and 3D version)
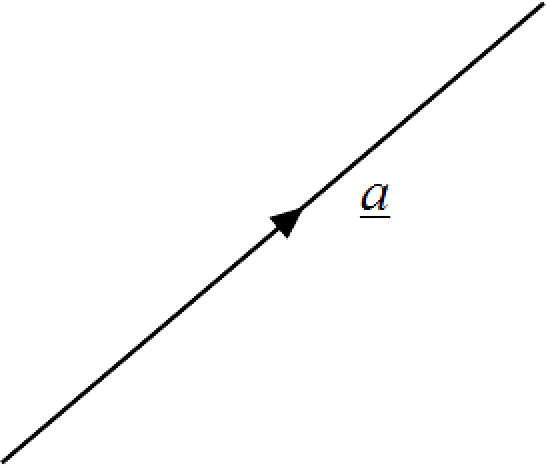
A vector in 2 or 3 dimensions can be represented by a directed line segment where the arrow on the line indicates the direction of the vector and the length of the line is proportional to the vector’s magnitude. To denote a vector joining two points $A$ and $B$ in the direction from initial point $A$ to terminal point $B$, as in the diagram, we write $\vec{AB}$.

Alternatively, we can represent a vector in bold type as, say, $a$, or underlined as, $\underline{a}$.
3.1. Components of a vector
In 2-D space a general vector, $\underline{a}$ can be written, $\underline{a} = \pmatrix{a_1\\a_2}$ where $a_1$ and $a_2$ are called the components of $\underline{a}$.
and represent the displacements in the $x$ and $y$ directions respectively.
A general vector in 3-D space has the form $\underline{a} = \pmatrix{a_1 \\ a_2 \\ a_3}$ with the components $a_1$, $a_2$ and $a_3$ corresponding to displacements in the $x$, $y$ and $z$ directions respectively.
The description can be extended to $n$-dimensional space but in this module we restrict our work to 2-D and 3-D.
Note that we use column notation for vectors but could equally well use row notation, e.g. $\underline{a} = (a_1, a_2)$.
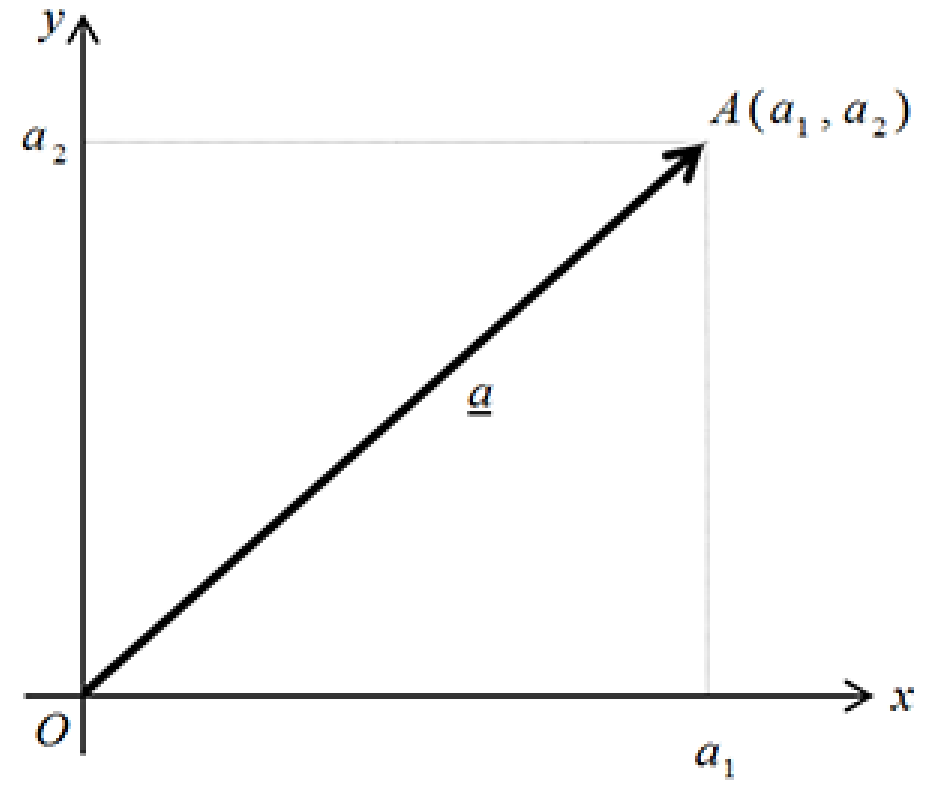
3.2. Position vectors
(i). Position vectors always start at the origin and end at a point in space. Suppose that, as in the diagram, we have a point $A(a_1, a_2)$ then the position vector of $A$, with respect to the origin $O(0, 0)$, is given by
$\underline{a} = \vec{OA} = \pmatrix{a_1 - 0 \\ a_2 - 0} = \pmatrix{a_1 \\ a_2}$.
Every point in the plane has an associated position vector.
Example 1
(i). In 2-D space the point $A(4, -7)$ has position vector, $\underline{a} = \vec{OA} = \pmatrix{\;\;\,4 \\-7}$.
(ii). In 3-D space the point $B(3, 5, -9)$ has position vector, $\underline{b} = \vec{OB} = \pmatrix{\;\;\,3 \\ \;\;\,5 \\ -9}$.
Note that the values we use for the vector are exactly the same as the coordinates of the point.
End of Example 13.3. Magnitude of a vector
The magnitude of a vector is denoted by $\mid {\vec{OA}} \mid $ or $\mid{\underline{a}}\mid$ and represents the length of $\vec{OA}$.
If the 2-D vector, $\underline{a} = \pmatrix{a_1 \\ a_2} $ then the magnitude of $\underline{a}$ is
$\mid {\underline{a}} \mid = \sqrt{a_1^2 + a_2^2}$.
In 3-D we have that a general vector $\underline{a} = \pmatrix{a_1 \\ a_2 \\ a_3}$ has magnitude,
$\mid \underline{a} \mid = \sqrt{a_1^2 + a_2^2 + a_3^2}$.
Example 2
Determine the magnitude of each the following vectors.
(i). $\underline{a} = \pmatrix{\;\;\,4 \\ -3} $ (ii). $\underline{b} = \pmatrix{0 \\ 6}$(iii). $\underline{c} = \pmatrix{\;\;\,4 \\ -2 \\ \;\;\,5}$
Solution
(i). $\mid {\underline{a}} \mid = \sqrt{4^2 + (-3)^2} = \sqrt{25} = 5$
(ii). $\mid {\underline{b}} \mid = \sqrt{0^2 + 6^2} = \sqrt{36} = 6$
(iii). $\mid {\underline{c}} \mid = \sqrt{4^2 + (-2)^2 + 5^2} = \sqrt{45} = 3\sqrt{5}$
End of Example 23.4. Equality of vectors
Two vectors are said to be equal if they have the same magnitude and the same direction.
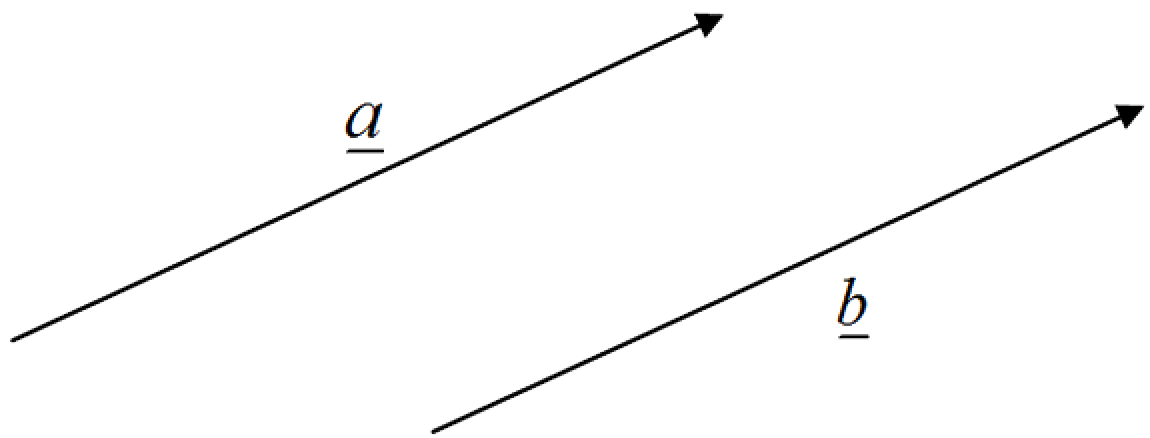
In the diagram $\underline{a}$ and $\underline{b}$ are two equal vectors as they have the same direction and the same magnitude, i.e. $\mid {\underline{a}} \mid = \mid {\underline{b}} \mid$.
Algebraically, two $n$-dimensional vectors,
$\underline{a} = \pmatrix{a_1 \\ a_2 \\ : \\ : \\a_n}$ and $\underline{b} = \pmatrix{b_1 \\ b_2 \\ : \\ : \\b_n}$.
are equal if and only if the components $a_i = b_i$ for all $i = 1, 2, ..., n$.
(Note that vectors must be the same size before they can be equal).
-
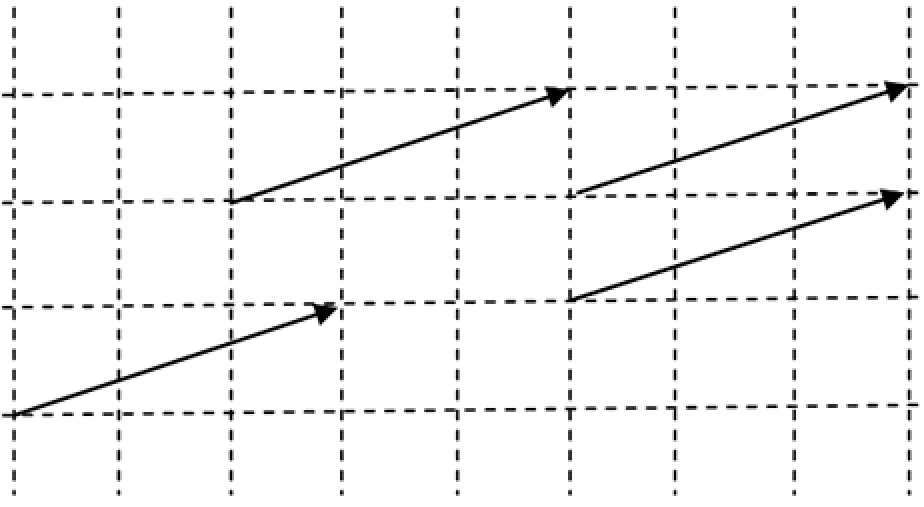
3.5. Free vectors in space
We can represent a vector by any line in space. The location of the line does not matter as long as it has the correct magnitude and direction. Hence, a vector does not necessarily start at the origin and can start at any point in the plane. All the lines in the diagram correspond to the same 2-D vector, i.e. each vector starts at a specific point and moves 3 units to the right and 1 unit up.
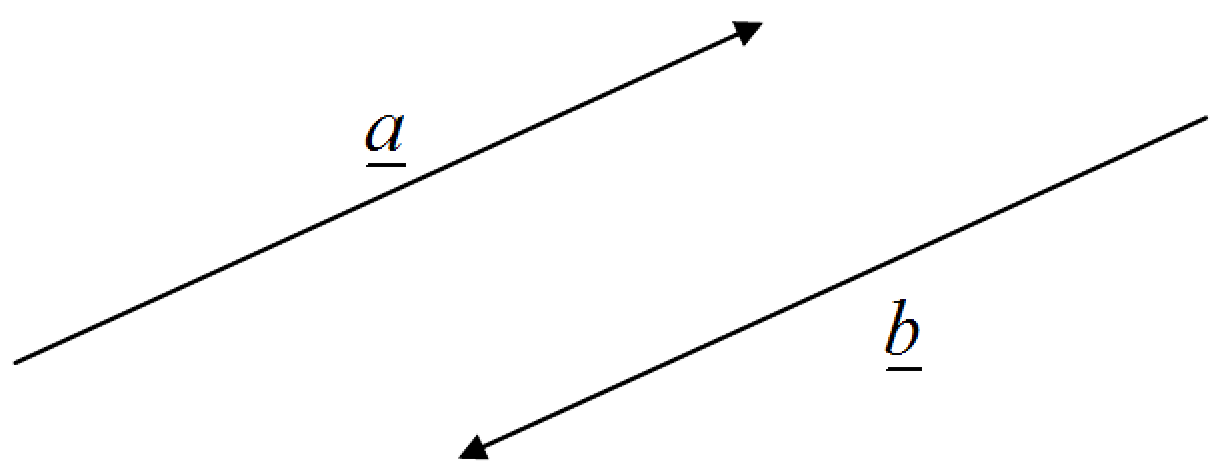
3.6. Negative vectors
A negative sign reverses the direction of a vector. In the diagram the vectors the $\underline{a}$ and $\underline{b}$ have the same magnitude but opposite directions. Hence, $\underline{a} = -\underline{b}$ .
3.7. Unit vectors
A unit vector is a vector of magnitude 1.
For any vector $\underline{a}$, the unit vector in the same direction as $\underline{a}$ is denoted
$\hat{\underline{a}} = {\Large\frac{\underline{a}}{\mid \underline{a} \mid}}$.
We shall see in Section 5 that in 2-D the unit vector in the direction of the $x$ axis is denoted by $\underline{i}$ and the unit vector in the direction of the $y$ axis is denoted by $\underline{j}$.
Example 3
For each of the following vectors find a unit vector that has the same direction.
(i). $\underline{a} = \pmatrix{-3 \\ \;\;\, 5}$ (ii). $\underline{b} = \pmatrix{\;\;\, 4 \\ \;\;\, 3 \\ -2}$ $\underline{b} = \pmatrix{1/ \sqrt{2} \\ 1/ \sqrt{2}}$.
Solution
(i). $\mid {\underline{a}} \mid = \sqrt{(-3)^2 + 5^2} = \sqrt{34}$.$\hat{\underline{a}} = {\Large\frac{\underline{a}}{\mid {\underline{a}}\mid}} = {\Large\frac{1}{\sqrt{34}}}\pmatrix{-3 \\ \;\;\, 5}$.
(ii). $\mid {\underline{b}} \mid = \sqrt{4^2 + 3^2 + (-2)} = \sqrt{29}$.$\hat{\underline{b}} = {\Large\frac{\underline{b}}{\mid {\underline{b}} \mid}} = {\Large\frac{1}{\sqrt{29}}}\pmatrix{\;\;\, 4 \\ \;\;\, 3 \\ -2}$.
(iii). $\mid {\underline{c}} \mid = \sqrt{\Bigg({{\Large\frac{1}{\sqrt{2}}}}\Bigg)^2 + \Bigg({{\Large\frac{1}{\sqrt{2}}}}\Bigg)^2} = \sqrt{{\Large\frac{1}{2}} + {\Large\frac{1}{2}}} = 1 $
As $\mid {\underline{c}} \mid\; = 1$ we have that $\underline{c}$ is itself a unit vector and so $\hat{\underline{c}} = \underline{c} = {\Large\frac{1}{\sqrt{2}}}\pmatrix{1 \\ 1}$.
End of Example 33.8. Zero vector
The zero vector is a vector with no direction and magnitude zero. It is written as either an underlined zero, $\underline{0}$ or a bold zero, $\bf{0}$. For example, the velocity of a stationary object is described by the zero vector.
Example 4
in 2-D: $\underline{0} = \pmatrix{0 \\ 0}$
and in 3-D: $\underline{0} = \pmatrix{0 \\ 0 \\ 0}$.
End of Example 4 -
4. Vector Operations
We now look at the arithmetic of vectors to include addition, subtraction and scalar multiplication. Multiplication of vectors is discussed briefly in Section 7.
4.1. Addition of vectors
Geometrically two vectors $\underline{a}$ and $\underline{b}$ are added by placing the tail of $\underline{b}$ at the tip of $\underline{a}$ and then drawing a line from the tail of $\underline{a}$ to the tip of $\underline{b}$. The two vectors we are adding make up two sides of a triangle and the sum of these two vectors, $\underline{a} + \underline{b}$ , is determined by the third side. This is called the 📷 triangle law for adding vectors.
Another way of adding two vectors is to place $\underline{a}$ and $\underline{b}$ tail-to-tail so that they both start at the same place. We then complete the figure to obtain a parallelogram. The diagonal of the parallelogram, with its origin at the point where $\underline{a}$ and $\underline{b}$ start, forms the vector $\underline{a} + \underline{b}$ . This is called the 📷 parallelogram law for adding vectors.
From an algebraic point of view vectors can be added provided they have the same dimensions.
Example 5
If $\underline{a} = \pmatrix{a_1 \\ a_2}$ and $\underline{b} = \pmatrix{b_1 \\ b_2}$ are two vectors in 2-D space then,
$\underline{a} + \underline{b} = \pmatrix{a_1 \\ a_2} + \pmatrix{b_1 \\ b_2}$
$ = \pmatrix{ a_1 + b_1 \\ a_2 + b_2}$
$ = \pmatrix{b_1 + a_1 \\ b_2 + a_2}$
$ = \pmatrix{b_1 \\ b_2} + \pmatrix{a_1 \\ a_2}$
$ = \underline{b} + \underline{a}$ .
This example shows vector addition is commutative.
End of Example 5Example 6
Given the vectors $ \underline{p} = \pmatrix{1 \\ 3}, \underline{q} = \pmatrix{2 \\ 5}, \underline{r} = \pmatrix{1 \\ 7 \\ 2}, \underline{s} = \pmatrix{1 \\ 1 \\ 3}$. Determine the following.
(i). $\underline{p} + \underline{q} = \pmatrix{1 \\ 3} + \pmatrix{2 \\ 5} = \pmatrix{3 \\ 8}$
(ii). $\underline{r} + \underline{s} = \pmatrix{1 \\ 7 \\ 2} + \pmatrix{1 \\ 1 \\ 3} = \pmatrix{2 \\ 8 \\ 5}$
End of Example 64.2. Subtraction of vectors
Subtraction of two vectors is just a special case of vector addition and can be modelled using either the triangle law or the parallelogram law. To subtract $\underline{b}$ from $\underline{a}$ we add $-\underline{b}$ to $\underline{a}$. Hence, referring to the 📷 diagram
Example 7
Given the vectors $\underline{p} = \pmatrix{1 \\ 3}, \underline{q} = \pmatrix{2 \\ 5}, \underline{r} = \pmatrix{1 \\ 7 \\ 2}, \underline{s} = \pmatrix{1 \\ 1 \\ 3}$ determine the following.
(i). $\underline{p} - \underline{q} = \pmatrix{1 \\ 3} - \pmatrix{2 \\ 5} = \pmatrix{-1 \\ -2}$
(ii). $\underline{q} - \underline{p} = \pmatrix{2 \\ 5} - \pmatrix{1 \\ 3} = \pmatrix{1 \\ 2}$
(iii). $\underline{r} - \underline{s} = \pmatrix{1 \\ 7 \\ 2} - \pmatrix{1 \\ 1 \\ 3} = \pmatrix{\;\;\,0 \\ \;\;\,6 \\ -1}$
End of Example 74.3. Multiplying a Vector by a Scalar
If we have a vector $\underline{a}$ and a positive scalar $k$, then we can define the product $k\underline{a}$ as a vector oriented in the same direction as $\underline{a}$ with a magnitude $k$ times that of $\underline{a}$. Multiplying by a negative scalar reverses the direction. In the 📷 diagram the vector represented by $-3\underline{a}$ is three times the magnitude of $\underline{a}$ but is directed in the opposite direction to $\underline{a}$.
If $ \underline{a} = \pmatrix{a_1 \\ a_2}$ and $k$ is any real number then multiplication by a real number $k$ gives
$k\underline{a} = k\pmatrix{a_1 \\ a_2} = \pmatrix{k a_1 \\ k a_2}$.
Example 8
If $\underline{a} = \pmatrix{1 \\ 3}$ and $\underline{b} = \pmatrix{1 \\ 7 \\ 2}$ determine the following.
(i). $2\underline{a} = 2\pmatrix{1 \\ 3} = \pmatrix{2 \\ 6}$
(ii). $5\underline{b} = 5\pmatrix{1 \\ 7 \\ 2} = \pmatrix{5 \\ 35 \\ 10}$
(iii). $-0.5\underline{a} = -0.5\pmatrix{1 \\ 3} = \pmatrix{-0.5 \\ -1.5}$
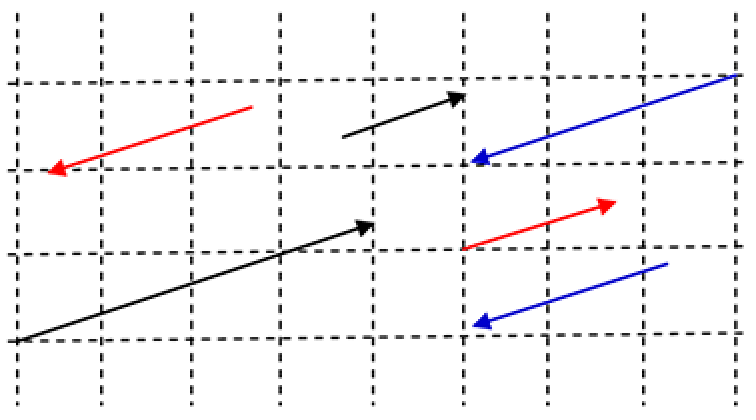
End of Example 84.4. Identifying parallel vectors
Two vectors are parallel if they have the same direction or have exact opposite directions. The diagram shows several parallel vectors. Recalling that scalar multiplication produces a new vector in the same direction as the original, or a vector with its direction reversed, we conclude that two vectors are parallel if one is a scalar multiple of the other. Hence, if two vectors $\underline{a}$ and $\underline{b}$ are parallel we must have that
$\underline{a} = k\underline{b}$
for some real number $k$.
Example 9
(i). $\underline{a} = \pmatrix{4 \\ 1}$ and $\underline{b} = \pmatrix{16 \\ \;\; 4}$ are parallel vectors since $\underline{a} = {\Large\frac{1}{4}}\underline{b}$.
(ii). if $\underline{a} = \pmatrix{-6 \\ \;\;\,2}$ and $\underline{b} = \pmatrix{3 \\ y}$, determine the value of $y$ that makes $\underline{a}$ and $\underline{b}$ parallel.
Solution
(ii). if $\underline{a}$ and $\underline{b}$ parallel vectors then
$\pmatrix{3 \\ y} = k\pmatrix{-6 \\ \;\;\, 2} = \pmatrix{-6k \\ \;\;\, 2k} $ (for some scaler $k$)
Hence, $-6k = 3 \implies k = -{\Large\frac{1}{2}}$
and $y = 2k \implies y = -1$
So, $\underline{b} = \pmatrix{\;\;\,3 \\ -1}$. Note that $\underline{b} = -{\Large\frac{1}{2}}\underline{a}$
End of Example 9X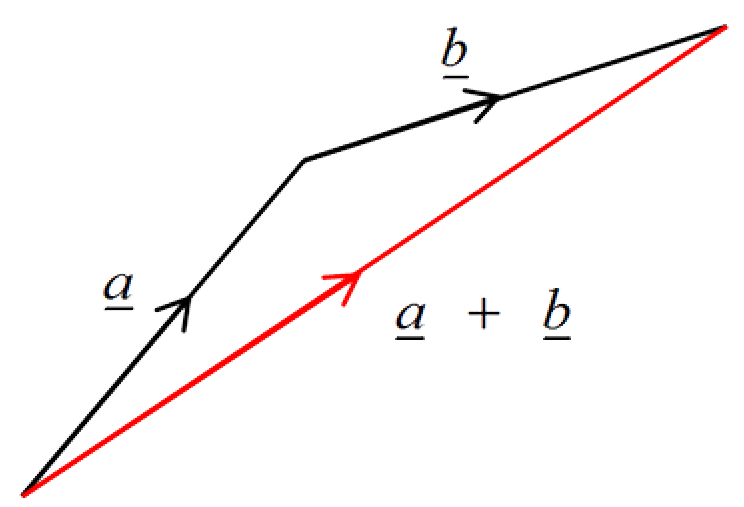 X
X X
X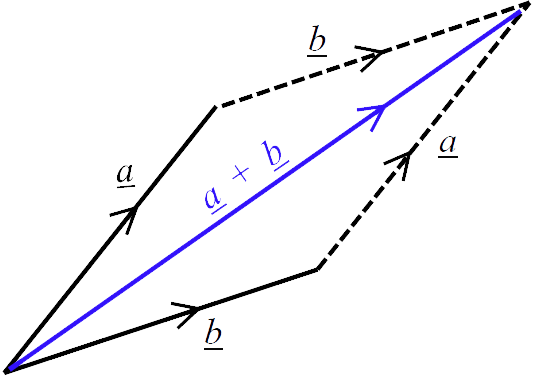 X
X$\underline{a} - \underline{b} = \underline{a} + (-\underline{b})$.
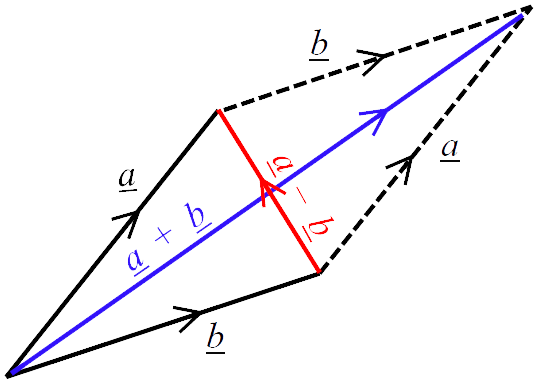
Note that the vector diagonals of a parallelogram are $\underline{a} + \underline{b}$ and $\underline{a} - \underline{b}$.
X
-
5. The Cartesian or rectangular component form of a vector
Using the definitions of vector addition and multiplication by a scalar, we can now develop an alternative algebraic representation of a two-dimensional vector.
A unit vector is a vector with magnitude equal to one unit. In 2-D we introduce two unit vectors, one parallel to the $x$-axis and one parallel to the $y$-axis; these we denote by $\underline{i}$ and $\underline{j}$ respectively:
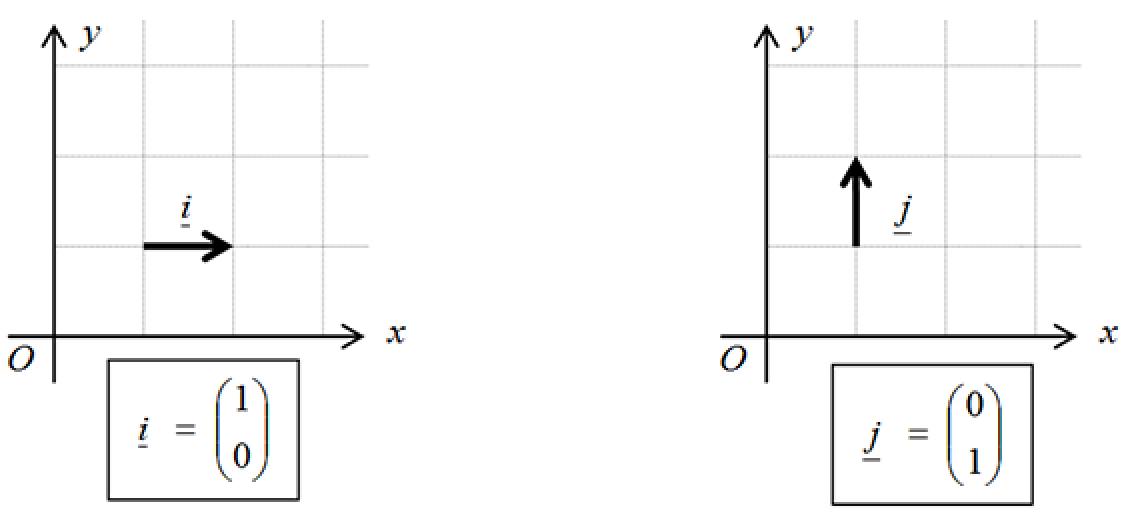
This means that any vector parallel to one of the axes can be expressed as a scalar multiple of either $\underline{i}$ or $\underline{j}$:
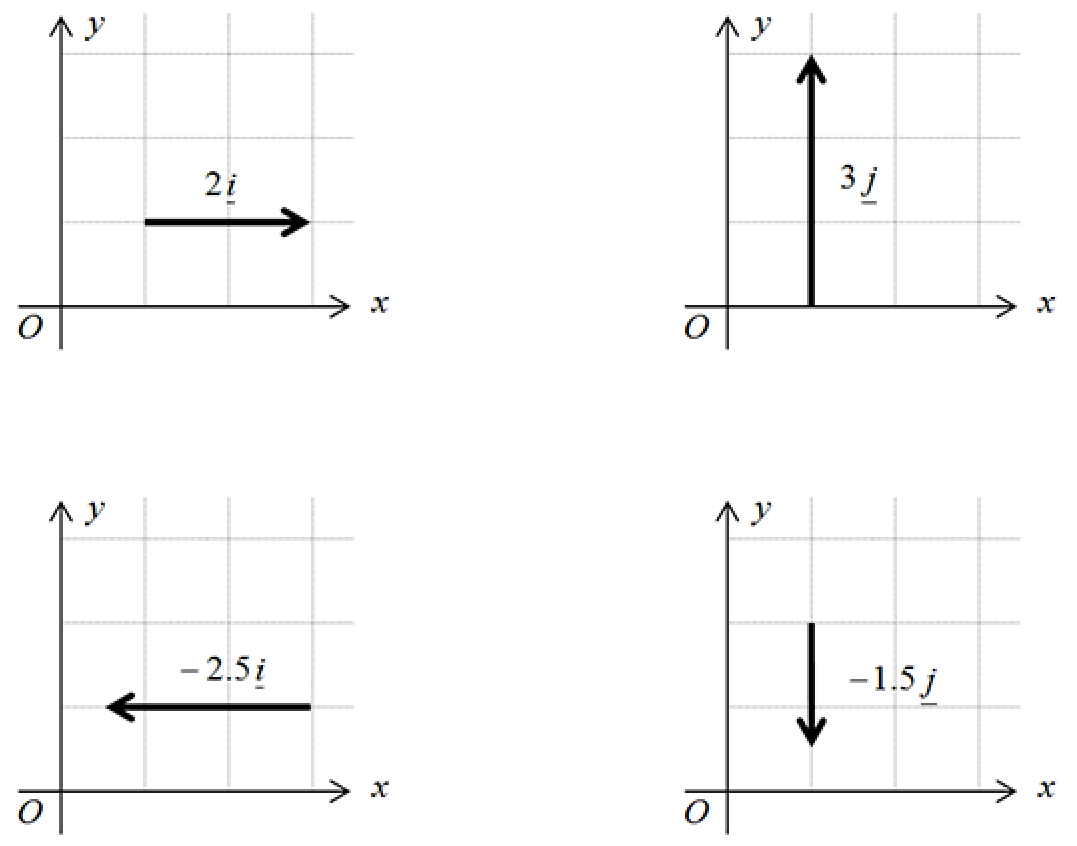
Bearing this, and the definition of vector addition, in mind we can take any two-dimensional vector $\underline{a}$ and decompose it into the sum of two component vectors, one parallel to the $x$-axis and one parallel to the $y$-axis:
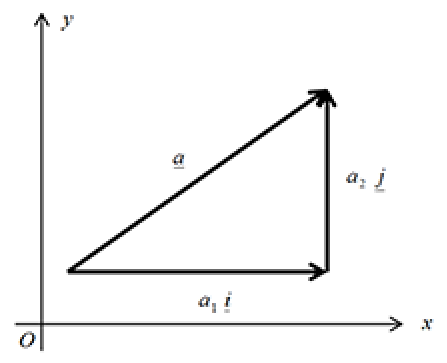
Algebraically we have
$\underline{a} = a_1\underline{i} + a_2\underline{j}$.
The vector is completely specified by the two values $a_1$ and $a_2$. These are the Cartesian or rectangular components of a vector in 2-D.
Multiplying a vector by a scalar is also easy in rectangular form:
If $\underline{a} = a_1i + a_2\,j$ then
$k\underline{a} = (ka_1)\underline{i} + (ka_2)\underline{j}$ for some scaler $k$.
Extension to Three Dimensions
The Cartesian form of a vector provides an easy and natural way of extending vectors into three dimensions. We take the $Oxy$ axes system and include a third axis, a $z$-axis, perpendicular to both the $x$ and $y$ axes:
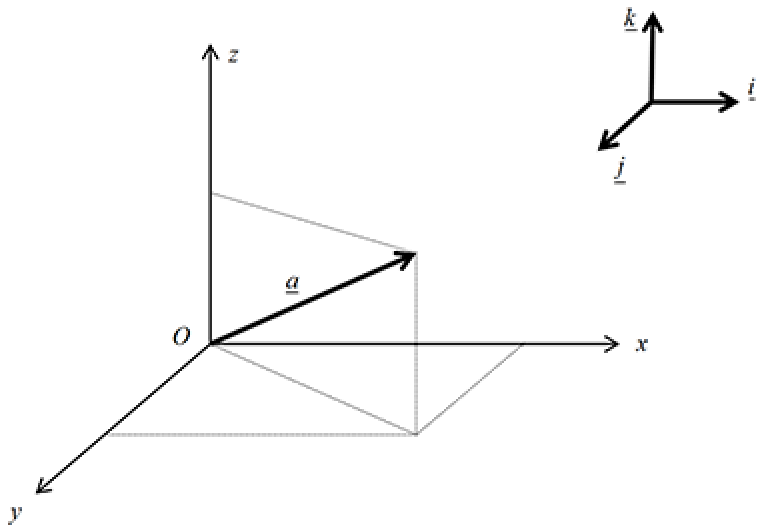
Denoting the unit vector parallel to the new $z$-axis by $\underline{k}$, any three-dimensional vector $\underline{a}$ can be decomposed into the sum of three component vectors, one in each of the axes directions:
$\underline{a} = a_1\underline{i} = a_2\underline{j} + a_3\underline{k}$
Example 10
Write the vectors $\underline{u} = \pmatrix{7 \\ 4} $ and $\underline{v} = \pmatrix{\;\;\,2 \\ -3 \\ \;\;\,6}$ in component form.
Solution
(i). $\underline{u} = 7\underline{i} + 4\underline{j}$ (ii). $\underline{v} = 2\underline{i} - 3\underline{j} + 6\underline{k}$
End of Example 10Example 11
Given $\underline{a} = 3\underline{i} + 2\underline{j}$ and $\underline{b} = 6\underline{i} - \underline{j}$ determine the following.
(i). $\underline{a} + \underline{b}$ (ii). $\underline{b} - \underline{a}$(iii). $4\underline{a}$ (iv). $2\underline{a} - 3\underline{b}$
(v). A unit vector in the same direction as the vector $\underline{a} + \underline{b}$
Solution
(i). $\underline{a} + \underline{b} = (3\underline{i} + 2\underline{j}) + (6\underline{i} - \underline{j})$
$= 3\underline{i} + 6\underline{i} + 2\underline{j} - \underline{j}$
$=\;$$9\underline{i}+\underline{j}$
(ii). $\underline{b} - \underline{a} = (6\underline{i} - \underline{j}) - (3\underline{i} + 2\underline{j})$
$= 6\underline{i} - 3\underline{i} - \underline{j} - 2\underline{j}$
$= \;$$3\underline{i}-3\underline{j}$
(iii). $4\underline{a} = 4(3\underline{i} + 2\underline{j})$
$=\;$$12\underline{i}+8\underline{j}$
(iv). $2\underline{a} - 3\underline{b} = 2(3\underline{i} + 2\underline{j}) - 3(6\underline{i} - \underline{j})$
$= 6\underline{i} + 4\underline{j} - 18\underline{i} + 3\underline{j}$
$=\;$$-12\underline{i}+7\underline{j}$
(v). From part (i). $\underline{a} + \underline{b} = 9\underline{i} + \underline{j}$
let $\underline{v} = 9\underline{i} + \underline{j}$.
Now$\mid \underline{v} \mid = \sqrt{9^2 + 1^2} =$$\sqrt{82}$
A unit vector in the same direction as $\underline{v} = \underline{a} + \underline{b}$ is,
$\mid \hat{\underline{v}}\mid = {\Large\frac{\underline{v}}{\mid \underline{v} \mid}} =\;$${\Large\frac{9}{\sqrt{82}}}\underline{i} + {\Large\frac{7}{\sqrt{82}}}\underline{j}$
End of Example 11Example 12
Consider the vector, $\underline{u} = 5\underline{i} + \underline{j} - 2\underline{k}$ and determine the following.
(i). A unit vector in the direction of $\underline{u}$.
(ii). A vector of magnitude 4 in the direction of $\underline{u}$.
Solution
(i). $\mid \underline{u} \mid = \sqrt{5^2 + 1^2 + (-2)^2} = \sqrt{30}$.
$\hat{\underline{u}} = \frac{\underline{u}}{\mid \underline{u} \mid} =\;$${\Large\frac{5}{\sqrt{30}}}\underline{i} + {\large\frac{1}{\sqrt{30}}}\underline{j} - {\Large\frac{2}{\sqrt{30}}}\underline{k}$.
(ii). The unit vector, $\hat{\underline{u}}$, found in part (i) has magnitude 1. Hence, to find a vector in the direction of $\hat{\underline{u}}$ with magnitude 4 we simply multiply $\hat{\underline{u}}$ by 4 giving
${\Large\frac{20}{\sqrt{30}}}\underline{i} + {\Large\frac{4}{\sqrt{30}}}\underline{j} - {\Large\frac{8}{\sqrt{30}}}\underline{k}$.
End of Example 12Example 13
Given that
$\underline{u} = \lambda \underline{i} + 2\underline{j}$
and
$\underline{v} = 2\underline{i} - \mu \underline{j}$
Determine the values of $\lambda$ and $\mu$ such that
$\underline{u} - \underline{v} = 9\underline{i} + 5\underline{j}$
Solution
We have that
$\underline{u} - \underline{v} = (\lambda \underline{i} + 2\underline{j}) - (2\underline{i} - \mu \underline{j})$
$= (\lambda - 2)\underline{i} + (2 + \mu)\underline{j}$
We require that
$\underline{u} - \underline{v} = 9\underline{i} + 5\underline{j}$
Hence,
$(\lambda - 2)\underline{i} + (2 + \mu)\underline{j} = 9\underline{i} + 5\underline{j}$
Equating coefficients of $\underline{i}$ and $\underline{j}$:
$\text{For} \underline{i} \text{:}\; \lambda - 2 = 9 \implies$ $\lambda = 11$.
$\text{For} \underline{j} \text{:}\; 2 + \mu = 5 \implies$ $\mu = 3$.
Check: $\underline{u} = 11\underline{i} + 2\underline{j}$ and $\underline{v} = 2\underline{i} - 3\underline{j}$.
Then: $\underline{u} - \underline{v} = 9\underline{i} + 5\underline{j}$ as required.
End of Example 13Example 14
Given that
$\underline{u} = 2\underline{i} - 3\underline{j}$
and
$\underline{v} = \underline{i} + \underline{j}$
Determine the value of the scalar $\alpha$ such that the vector
$\underline{w} = \underline{u} + \alpha \underline{v}$ is parallel to the vector $\underline{i}$.
Solution
We have that
$\underline{w} = \underline{u} + \alpha \underline{v} = 2\underline{i} - 3\underline{j} + \alpha(\underline{i} + \underline{j})$
$= (2 + \alpha)\underline{i} + (-3 + \alpha)\underline{j}$
if $\underline{w}$ is parallel to $\underline{i}$ then $\underline{w} = \lambda \underline{i}$ for some scaler $\lambda$.
Hence, we require $\pmatrix{\;\;\,2 + \alpha \\ -3 + \alpha} = \lambda \pmatrix{1 \\ 0}$
$2 + \alpha = \lambda$
$-3 + \alpha = 0$
The second equation gives $\alpha = 3$ and from the first equation, $\lambda = 5$.
Check: $\underline{w} = (2 + \alpha)\underline{i} + (-3 + \alpha)\underline{j} = 5\underline{i}$.
With $\alpha = 3$ we have $\underline{w} = 5\underline{i}$ which is a vector parallel to the vector $\underline{i}$.
End of Example 14 -
6. Relative position vectors
Suppose we have two points $A(a_1, a_2)$ and $B(b_1, b_2)$ as shown
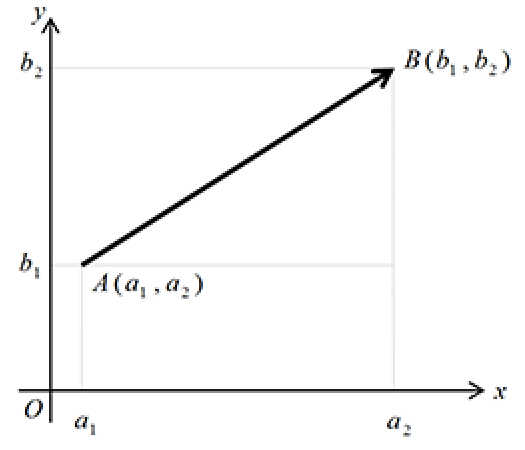
The vector $\vec{AB}$ with initial point $A$ and terminal point $B$ and is called the position vector of $B$ relative to $A$. Note that $\vec{AB}$ is also known as a displacement vector as it represents the displacement of $B$ from $A$. The Cartesian components of $\vec{AB}$ are easily determined from the coordinates of the points as:
$\vec{AB} = \pmatrix{b_1 - a_1 \\ b_2 - a_2}$.
Example 15
Referring to the diagram below, determine the position vector of $B$ relative to $A$ in terms of $\underline{a}$ and $\underline{b}$.
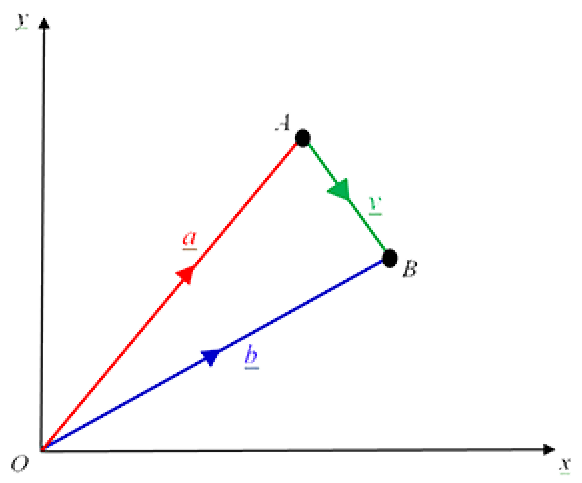
Solution
$\underline{v} = \vec{AB} = \vec{AO} + \vec{OB}$
$= -\vec{OA} + \vec{OB}$
$= \vec{OB} - \vec{OA}$
$= \underline{b} - \underline{a}$.
End of Example 15Example 16
Determine the components of the vector $\underline{v} = \vec{AB}$ with initial point $A(3,-2)$ and terminal point $B(-1, 2)$.
Solution
The points are plotted in the diagram below:
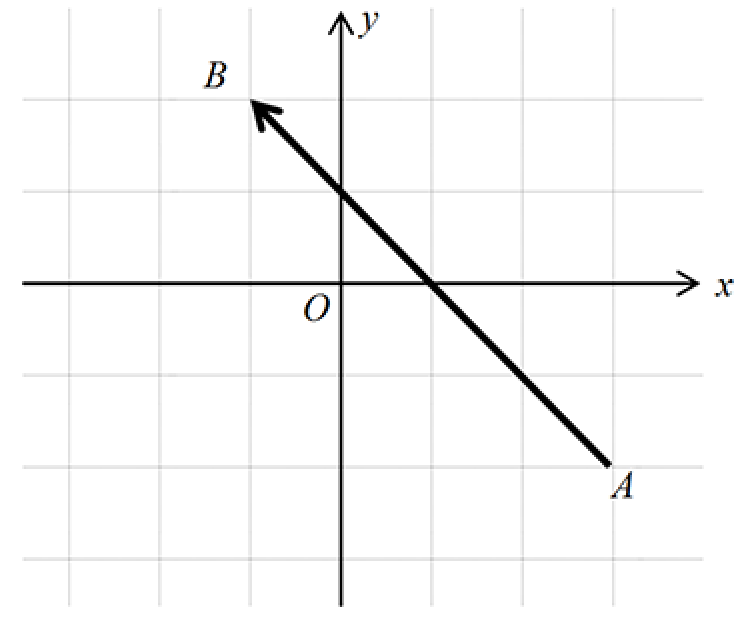
The points $A$ and $B$ have position vectors $\underline{a} = \pmatrix{\;\;\,3 \\ -2}$ and $\underline{b} = \pmatrix{-1 \\ \;\;\,2}$ respectively.
Hence, $\vec{AB} = \underline{b} - \underline{a} = \pmatrix{-1 \\ \;\;\,2} - \pmatrix{\;\;\,3 \\ -2} = \pmatrix{-4 \\ \;\;\,4}$.
The diagram confirms that to go from $A$ to $B$ we move 4 units in the negative $x$-direction and 4 units in the positive $y$-direction.
End of Example 16Example 17
Let $P$ be the point $(2, -4, 3)$ and $Q$ be the point $(6, -1, -5)$. Determine the vector $\vec{PQ}$.
Solution
The points $P$ and $Q$ have position vectors $\underline{p} = \pmatrix{\;\;\,2 \\ -4 \\ \;\;\,3}$ and $\underline{q} = \pmatrix{\;\;\,6 \\ -1 \\ -5}$ respectively.
Hence. $\vec{PQ} = \underline{q} - \underline{p} = \pmatrix{\;\;\,6 \\ -1 \\-5} - \pmatrix{\;\;\,2 \\ -4 \\ \;\;\,3} = \pmatrix{\;\;\,4 \\ \;\;\,3 \\ -8}$.
End of Example 17Example 18
(a). Relative to a fixed origin the points $A, B$ and $C$ have coordinates $(3, -2)$, $(4, 1)$ and $(-6, 0)$ respectively.
(i). Determine the vectors $\vec{AB}$ and $\vec{CB}$.
(ii). What is the length of the vector $\vec{CA}$?
Solution
(i). The position vectors are $\underline{a} = \pmatrix{\;\;\,3 \\ -2}, \underline{b} = \pmatrix{4 \\ 1}$ and $\underline{c} = \pmatrix{-6 \\ \;\;\,0}$.
$\vec{AB} = \underline{b} - \underline{a} = \pmatrix{4 \\ 1} - \pmatrix{\;\;\,3 \\ -2} = \pmatrix{1 \\ 3}$
$\vec{CB} = \underline{b} - \underline{c} = \pmatrix{4 \\ 1} - \pmatrix{-6 \\ \;\;\,0} = \pmatrix{10 \\ \;\;\,1}$
(ii). $\vec{CA} = \underline{a} - \underline{c} = \pmatrix{\;\;\,3 \\ -2} - \pmatrix{-6 \\ \;\;\,0} = \pmatrix{\;\;\,9 \\ -2}$
The magnitude of the vector $\vec{CA}$ is, $\mid \vec{CA} \mid = \sqrt{9^2 + (-2)^2} = \sqrt{85}$.
(b). The points $P$ and $Q$ have coordinates $(4, 2, -1)$ and $(7, 3, -3)$ respectively.
Determine the magnitude of the vector $\vec{PQ}$.
$\vec{PQ} = \vec{QO} - \vec{OP} = \pmatrix{\;\;\,7 \\ \;\;\,3 \\-3} - \pmatrix{\;\;\,4 \\ \;\;\,2 \\ -1} = \pmatrix{\;\;\,3 \\ \;\;\,1 \\ -2}$
The magnitude of the vector $\vec{PQ}$ is, $\mid \vec{PQ} \mid = \sqrt{3^2 + 1^2 + (-2)^2} = \sqrt{14}$.
End of Example 18 -
7. The scalar (dot) product of two vectors
We now extend the arithmetic of vectors and introduce a method of multiplying two vectors together. There are, in fact, two ways of multiplying vectors: one produces a scalar while the other returns a vector. In this module we are only concerned with the former, i.e. the method that results in a scalar product.
Consider two vectors $\underline{a}$ and $\underline{b}$ whose orientations differ by an angle $\theta$, as shown in the diagram. :
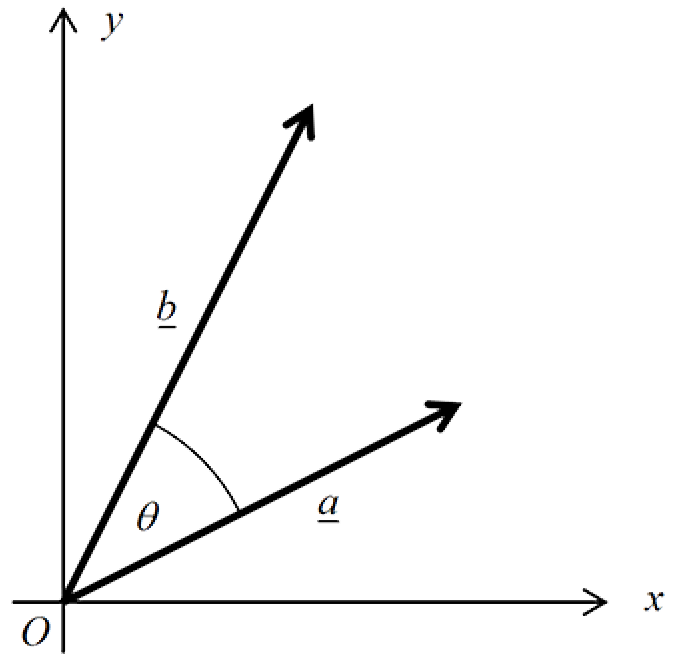
The scalar product of $\underline{a}$ and $\underline{b}$ is defined as
$\underline{a} \cdot \underline{b} = \mid \underline{a}\mid \mid \underline{b} \mid cos\; \theta$
and is often referred to as the dot product.
This course does not include trigonometry and so we use an alternative definition which calculates the scalar product directly from the components of the vectors.
For two (2-D) vectors, $\underline{a} = \pmatrix{a_1 \\ a_2}$ and $ \underline{b} = \pmatrix{b_1 \\ b_2}$, it can be shown that
$\underline{a} \cdot \underline{b} = a_1b_1 + a_2b_2 $.
This result generalises to $n$ dimensions.
Knowledge of the scalar product will be required in the next unit for matrix multiplication.
Example 19
(i). Determine the scalar product of, $\underline{a} = \pmatrix{7 \\ 2}$ and $\underline{b} = \pmatrix{6 \\ 1}$.
(ii). Determine the scalar product of, $\underline{c} = 3\underline{i} - \underline{j}$ and $\underline{d} = -6\underline{i} - 2\underline{j}$.
(iii). Determine the scalar product of, $\underline{p} = \pmatrix{1 \\ 7 \\ 2}$ and $\underline{q} = \pmatrix{1 \\ 1 \\ 3}$.
(iv). Determine the scalar product of, $\underline{u} = 5\underline{i} + \underline{j} - 2\underline{k}$ and $\underline{v} = 3\underline{i} + 2\underline{k}$.
Solution
(i). $\underline{a} \cdot \underline{b} = 7 \times 6 + 2 \times 1 =\; $$\class{double}{4}$$\class{double}{4}$
(ii). $\underline{c} \cdot \underline{d} = 3 \times (-6) + (-1) \times (-2) =\;$$\class{double}{-}$$\class{double}{1}$$\class{double}{6}$
(iii). $\underline{p} \cdot \underline{q} = 1 \times 1 + 7 \times 1 + 2 \times 3 = \;$$\class{double}{1}$$\class{double}{4}$$\class{double}{.}$
(iv). $\underline{u} \cdot \underline{v} = 5 \times 3 + 1 \times 0 + (-2) \times 2 = \;$ $\class{double}{1}$$\class{double}{1}$$\class{double}{.}$
An important application of the scalar product is in determining whether two vectors are perpendicular.
The definition of the scalar product of two vectors $\underline{a}$ and $\underline{b}$ stated,
$\underline{a} \cdot \underline{b} = \mid \underline{a} \mid \mid \underline{b} \mid cos \; \theta$
Now, if $\underline{a}$ and $\underline{b}$ are non-zero vectors but we find that $\underline{a} \cdot \underline{b} = 0$ then we must have that $cos(\theta) = 0$ and so $\theta = 90^o$ meaning that $\underline{a}$ and $\underline{b}$ are perpendicular.
End of Example 19Example 20
(i). If $\underline{a} = a_1\underline{i} + a_2\underline{j}$ determine $\underline{a} \cdot \underline{a}$ and $\mid \underline{a} \mid$. Comment on the result.
Solution
The scalar product of $\underline{a}$ with itself is,
$\underline{a} \cdot \underline{a} = a_1 \times a_1 + a_2 \times a_2 = \;$$a_1^2+a_2^2$
The magnitude of $\underline{a}$ is,
$\mid \underline{a} \mid = \;$$\sqrt{a_1^2 + a_2^2}$.
This example shows that, $\underline{a} \cdot \underline{a} = \mid \underline{a} \mid^2$
(ii). Show that the result in part (i) holds when $\underline{a} = 3\underline{i} + 4\underline{j}$.
Solution
The scalar product of $\underline{a}$ with itself is,
$\underline{a} \cdot \underline{a} = 3 \times 3 + 4 \times 4 =\;$$\class{double}{2}$$\class{double}{5}$$\class{double}{.}$
The magnitude of $\underline{a}$ is,
$\mid \underline{a} \mid \;= \sqrt{3^2 + 4^2} =\;$$\sqrt{25}$.
Hence, $\underline{a} \cdot \underline{a} = \mid a \mid^2 = 25$ as expected.
End of Example 20Example 21
Show that the following vectors are perpendicular.
(i) . $\underline{a} = 2\underline{i} + 6\underline{j}$ and $\underline{b} = -3\underline{i} + \underline{j}$.
(ii). $\underline{w} = 3\underline{i} + 2\underline{j} - \underline{k}$ and $\underline{z} = \underline{i} - 2\underline{j} - \underline{k}$.
Solution
(i). $\underline{a} \cdot \underline{b} = 2 \times (-3) + 6 \times 1 = 0$
As the scalar product of $\underline{a}$ and $\underline{b}$ is zero the vectors are perpendicular.
(ii). $\underline{v} \cdot \underline{w} = 3 \times 1 + 2 \times (-2) + (-1) \times (-1) = 0$.
As the scalar product of $\underline{v}$ and $\underline{w}$ is zero the vectors are perpendicular.
End of Example 21 -
Summary
- In this unit we introduced vectors and you should now be able to:
- identify whether physical quantities are scalars or vectors.
- add and subtract vectors algebraically and graphically.
- perform scalar multiplication of a vector and interpret the result graphically.
- calculate the magnitude of a vector.
- determine a unit vector in the direction of a given vector.
- express the position vector of a point as a column vector.
- express the position vector of a point in Cartesian component form.
- Calculate the scalar product of two vectors.
- Determine whether two vectors are perpendicular.
You should now attempt the tutorial exercises and Maple questions on GCU Learn.
In the next unit we take an introductory look at matrices and their properties.