-
1. Introduction
- This unit introduces the theory and application of mathematical structures known as matrices. With the advent of computers matrices have become widely used in the mathematical modelling of practical real-world problems in computing, engineering and business where, for example, there is a need to analyse large data sets. Some examples of the applications of matrices include:
- in computer graphics to project three dimensional images onto two dimensional screens and apply transformations to rotate and move these screen objects.
- in all areas of science to solve (large) systems of equations.
- in cryptography to encode messages, computer files, PIN numbers, etc.
- in business to formulate and solve linear programming problems to optimise resources subject to a set of constraints.
We begin by defining basic operations with matrices including addition, subtraction and scalar multiplication. Matrix multiplication is then introduced and we identify conditions which determine whether or not matrices are conformable for multiplication. Next we briefly look at special types of matrices and their properties before moving on to look at the determinant of a matrix and the concept of an inverse matrix. We then present some applications of matrices including; solving systems of linear equations, transforming objects on computer screens, encrypting and decrypting data and the modelling of graphs and networks.
-
2. Definitions
Before we undertake calculations involving matrices it is firstly necessary to present some definitions and terminology.
2.1. What is a matrix?
A matrix is an ordered rectangular array of numbers and/or variables arranged in rows and columns and enclosed in brackets. For our purposes these elements will take the form of real numbers. In general, matrices are denoted by upper case letters.
Example 1
The following are all matrices:
(i). $A = \pmatrix {0 & \;\,\,4 \\ 1 & -1}$
(ii). $B = \pmatrix {\;50 & 25 & \;45 \\ 125 & 80 & \;60 \\ \;60 & 0 & \;75 \\ \;90 & 80 & 110}$.
(iii). $K = \pmatrix{\;\;\,1.2 & 3.8 & 0.2 & -0.2 & 3.1 \\ -2.3 & 2.1 & 3.6 & \;\;\,3.8 & 0.1}$
(iv). $M = \pmatrix{3 \\ 1}$.
End of Example 12.2. Rows and columns of a matrix
Another useful approach to the structure of a matrix is to look at the rows and columns of the matrix. These are simple and obvious concepts; but we need to know that the rows are numbered starting from the top (i.e. Row 1) and the columns are numbered starting from the left hand side of the matrix (i.e. Column 1).
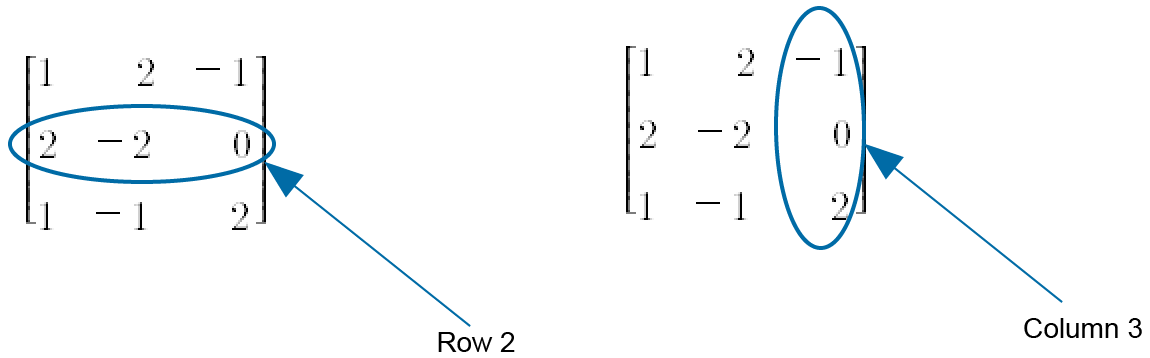
2.3. Order of a matrix
The order, also called the size or dimension, of a matrix is identified by a number pair in the form $m \times n$ , where $m$ is the number of rows in the matrix and $n$ the number of columns.
$A = \pmatrix{a_{11} & a_{12} & \cdots & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & \cdots & a_{2n} \\ \vdots & & \ddots & &\vdots \\ \vdots & & & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & \cdots & a_{mn}} $
We say that the matrix $A$ is a “$m$ by $n$ matrix”.
A matrix with the same number of rows as columns is called a square matrix.
Example 2
The matrices in Example 1 have the following sizes,
(i). $A$ is a $2 \times 2$ matrix, i.e. 2 rows and 2 columns.
(ii). $B$ is a $4 \times 3$ matrix, i.e. 4 rows and 3 columns.
(iii). $K$ is a $2 \times 5$ matrix, i.e. 2 rows and 5 columns.
(iv). $M$ is a $2 \times 1$ matrix, i.e. 2 rows and 1 column.
We actually encountered matrices of the type in part (iv) in the previous unit when we looked at vectors. If a matrix has only one column, i.e. a $m \times 1$ matrix, it can be thought of as a column vector with $m$ components and if it only has one row, i.e. a $1 \times n$ matrix, it can be thought of as a row vector with $n$ components.
End of Example 22.4. Element of a matrix
Each element, or entry, in a matrix is denoted by a lower case letter, with appropriate subscripts, indicating its row and column position. Hence, element $a_{ij}$ is located in the $i$-th row and $j$-th column of the matrix $A$ below.
$A = \pmatrix{a_{11} & a_{12} & \cdots & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & \cdots & a_{2n} \\ \vdots & & \ddots & &\vdots \\ \vdots & & & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & \cdots & a_{mn}} $
Example 3
For the matrix $A = \pmatrix{\;\,50 & \;\;\,25 & -45 \\ \,125 & \;\;\,80 & \;\;\,60 \\ \;\;60 & -50 & \;\;\,75 \\ \;\,90 & \,120 & \,110 }$
(i). element $a_{43} = 110$, as it is located at Row 4, Column 3.
(ii). element $a_{32} = -50$ , as it is located at Row 3, Column 2.
We can easily draw parallels between matrices and computer arrays as used in programming languages. For example, in C++ if $A$ is an array we would use the syntax $A[2][3]$ to index the element in the second row and third column of $A$, in Maple we would use the notation $A[2, 3]$.
End of Example 32.5. Equality of matrices
- Two matrices $A$ and $B$ are equal if and only if:
- they are of the same size, i.e. both are $m \times n$ matrices
- their corresponding elements are the same, i.e. $a_{ij} = b_{ij}$ for $i = 1, ..., m$ and $j = 1,...,n$.
Example 4
Determine the values of $w, x, y$ and $z$ that guarantee the matrices $A$ and $B$ are equal,
$A = \pmatrix{4 & x \\ x+z & 0}$, $B = \pmatrix{y & 6 \\ 7 & w}$
Solution
We require $w = 0,\; x = 6,\; y = 4,\; x + z = 7 \implies z = 1$.
End of Example 4 -
3. Operations with matrices
We now look at some basic arithmetic operations with matrices.
3.1. Matrix addition
- Two matrices can be added if and only if they are of the same size.
- To add two matrices we add corresponding elements.
- The result of the addition is a matrix of the same size.
- Matrix addition is commutative, i.e. $A + B = B + A$, see parts (ii) and (iii) in the following example.
Example 5
In each of the following carry out the specified addition.
(i). $\pmatrix{\;\;50 & \;\;25 & \;\;45 \\ 125 & \;\;80 & \;\;60 \\ \;\;60 & \;\;80 & \;\;75 \\ \;\;90 & 120 & 110} + \pmatrix {-50 & 35 & \;\;\,45 \\ -25 & 80 & -70 \\ -80 & 10 & \;\,-5 \\ \;\;\,90 & 20 & -135} = \pmatrix{\;\;\;0 & \;\;\,60 & \;\;\,90 \\ \,100 & \,160 & -10 \\ -20 & \;\;\,90 & \;\;\,70 \\ \,180 & \,140 & -25}$
(ii). $\pmatrix {2 & -1 \\3 & \;\;\,6} + \pmatrix{\;\;\,0 & 4 \\ -2 & 5} = \pmatrix{2 & \;\,3 \\ 1 & 11}$
(iii). $\pmatrix{\;\;\,0 & 4 \\ -2 & 5} + \pmatrix{2 & -1 \\ 3 & \;\;\,6} = \pmatrix{2 & \;\,3 \\ 1 & 11}$
End of Example 53.2. Matrix subtraction
- Two matrices $A$ and $B$ can be subtracted if and only if they are of the same size.
- To form $A - B$ subtract each element of $B$ from the corresponding element of $A$.
- The result of the subtraction is a matrix of the same size.
- As for subtraction of real numbers, matrix subtraction is not commutative, i.e. $A - B \neq B - A$, see the next example.
Example 6
In the following carry out the specified subtraction.
(i). $\pmatrix{3 & 1 & -2 \\ 4 & 0 & \;\;\,8} - \pmatrix{2 & -3 & -1 \\ 2 & -5 & \;\;\,1} = \pmatrix{1 & 4 & -1 \\ 2 & 5 & \;\;\,7}$
(ii). $\pmatrix{2 & -3 & -1 \\ 2 & -5 & \;\;\,1} - \pmatrix{3 & 1 & -2 \\ 4 & 0 & \;\;\,8} = \pmatrix{-1 & -4 & \;\;\,1 \\ -2 & -5 & -7}$
End of Example 63.3. Scalar multiplication of a matrix
- Any matrix can be multiplied by a number (scalar) and this procedure is referred to as scalar multiplication.
- Scalar multiplication is performed by multiplying each element in the matrix by the number.
- Scalar multiplication must not be confused with matrix multiplication which will be defined later.
Example 7
Simplify each of the following by performing the scalar multiplication.
(i). $2\pmatrix{0 & \;\;\,4 \\1 & -1} = \pmatrix{0 & \;\;\,8 \\ 2 & -2}$
(ii). $-0.1\pmatrix{-3 \\ -2 \\ \;\;\,0 \\ \;\;\,2} = \pmatrix{\;\;0.3 \\ \;\;0.2 \\ \;\;\;\;0 \\ -0.2}$
End of Example 7Example 8
Let $A = \pmatrix{1 & 1 & 2 \\ 2 & 3 & 4}, B = \pmatrix{0 & -1 & \;\;\,0 \\ 1 & \;\;\,0 & -1}$ and $C = \pmatrix{\;\;\,1 & 0 \\ -9 & 4}$
If possible simplify each of the following:
(i). $2A + 3B$, (ii). $3B - 2A$(iii). $C - A$
Solution
(i). $2A + 3B = 2\pmatrix{1 & 1 & 2 \\ 2 & 3 & 4} + 3\pmatrix{0 & -1 & \;\;\,0 \\ 1 & \;\;\,0 & -1}$
$=\; \pmatrix{2 & 2 & 4 \\ 4 & 6 & 8} + \pmatrix{0 & -3 & \;\;\,0 \\ 3 & \;\;\,0 & -3}$
$=\; \pmatrix{2 & -1 & 4 \\ 7 & \;\;\,6 & 5}$
(ii). $3B - 2A = 3\pmatrix{0 & -1 & \;\;\,0 \\ 1 & \;\;\,0 & -1} - 2\pmatrix{1 & 1 & 2 \\ 2 & 3 & 4}$
$=\; \pmatrix{0 & -3 & \;\;\,0 \\ 3 & \;\;\,0 & -3} - \pmatrix{2 & 2 & 4 \\ 4 & 6 & 8}$
$=\; \pmatrix{-2 & -5 & \;\;-4 \\ -1 & -6 & -11}$
(iii). We are unable to calculate $C - A$ as the matrices have different dimensions.
Here $C$ is a $2 \times 2$ matrix while $A$ is a $2 \times 3$ matrix.
End of Example 83.4. Matrix Multiplication
- Matrix multiplication can only be carried out between matrices which are conformable for matrix multiplication.
- Two matrices $A$ and $B$, with sizes $m \times n$ and $p \times q$ respectively, are conformable for multiplication, $A \times B$, if and only if $n = p$ ; i.e the number of columns of $A$ is the same as the number of rows of $B$.
- The result of the matrix multiplication, $A \times B$ is usually written $AB$.
- Note that matrix multiplication may be defined for $AB$ but not necessarily for $BA$. Hence, matrix multiplication is not in general commutative.
- The result of multiplying a $m \times n$ matrix and a $p \times q$ matrix, where $n = p$, is a $m \times q$ matrix.
Note: If the “inner dimensions” $n$ and $p$ are equal we can multiply the matrices and the resulting product matrix has size given by the “outer dimensions”, i.e. $m \times q$.
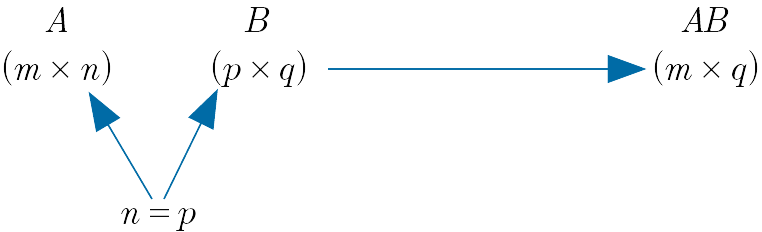
If required further resources on multiplication of matrices can be found at:
🔗 http://www.mathcentre.ac.uk/topics/matrices/matrix-arithmetic/
Example 9
Determine which of the following matrices are conformable for matrix multiplication
$A = \pmatrix{1 & \;\;\,2 & 3 \\ 4 & -5 & 6}, B = \pmatrix{1 & 2 \\ 3 & 4}, C = \pmatrix{1 & \;\;\,2 \\ 2 & \;\;\,4 \\ 3 & -1}$.
Solution
The matrix $A$ is $2 \times 3$.
The matrix $B$ is $2 \times 2$.
The matrix $C$ is $3 \times 2$.
(i). First consider the matrix product $AB$.
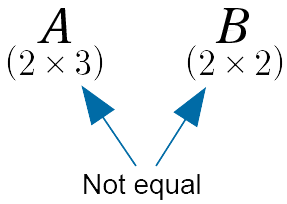
The “inner dimensions” are not equal and so we cannot perform the matrix multiplication. The number of columns in $A(3)$ does not equal the number of rows in $B( 2)$.
(ii). Now consider the matrix product $AC$.
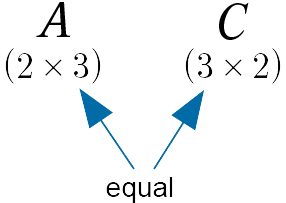
The “inner dimensions” are equal and so we can perform the matrix multiplication and the product matrix will have size given by the “outer dimensions”, i.e. $2 \times 2$.
Exercise: Confirm the following: $BA, AC, CA, CB$ and $BB$ are valid multiplications; whereas we cannot calculate $AB, BC, AA$ or $CC$.
End of Example 93.4.1. Matrix multiplication and the scalar (dot) product
To multiply two matrices, conformable for matrix multiplication, involves an extension of the scalar (dot) product procedure described in the previous unit on vectors.
To form the result of multiplying $A$ (on the left) by $B$ (on the right) (i.e. to form the product $AB$) we view $A$ as a matrix composed of rows and $B$ as a matrix made up of columns.
The entries in the product matrix are determined by forming dot products.
To determine the element in Row $i /$ Column $j$, i.e. position $( i, j )$, of $AB$ we form the dot product of Row $i$ of matrix $A$ with Column $j$ of matrix $B$.
Example 10
Let $A = \pmatrix{\;\;\,1 & 6 & -2 \\ \;\;\,3 & 0 & \;\;\,3 \\ -2 & 3 & -1}$ and $B = \pmatrix{1 & \;\;\,2 \\ 1 & -2 \\ 3 & \;\;\,0}$
The product matrix $AB$ can be calculated as $A$ has size $3 \times 3$ and $B$ has size $3 \times 2$, i.e. the number of columns of $A$ is the same as the number of rows of $B$.
Hence, the product matrix, $AB$ will have size $3 \times 2$.
For example, to obtain the element in Row 1/Column 1, i.e. position $(1, 1)$ of $AB$ we take the dot product of Row 1 of $A$ with Column 1 of $B$, i.e.
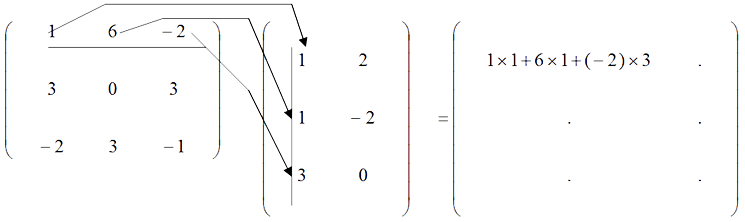
To obtain the element in Row 1/Column 2, i.e. position $(1, 2)$ we take the dot product of Row 1 of $A$ with Column 2 of $B$.
In vector form we have
$\pmatrix{1 & 6 & -2}. \pmatrix{\;\;\,2 \\ -2 \\ \;\;\,0} = 1 \times 2 + 6 \times (-2) + (-2) \times 0 = -10$.
This process can be continued to generate the 6 components of the $3 \times 2$ product matrix, $AB$.
$\pmatrix{\;\;\,1 & 6 & -2 \\ \;\;\,3 & 0 & \;\;\,3 \\ -2 & 3 & -1}\pmatrix{1 & \;\;\,2 \\ 1 & -2 \\3 & \;\;\,0} = \pmatrix{1 \times 1 + 6 \times 1 + (-2) \times 3 & 1 \times 2 + 6(-2) + (-2) \times 0 \\ 3 \times 1 + 0 \times 1 + 3 \times 3 & 3 \times 2 + 0 \times (-2) + 3 \times 0 \\ -2 \times 1 + 3 \times 1 + (-1) \times 3 & -2 \times 2 + 3 \times (-2) + (-1) \times 0} = \pmatrix{\;\;\,1 & -10 \\ \;\;12 & \;\;\;\,6 \\ -2 & -10}$
End of Example 10Example 11
Let $A = \pmatrix{0 & \;\;\;4 \\ 1 & -1}$ and $B = \pmatrix{1 & \;\;\;1 \\ 2 & -1}$. If possible calculate $AB$ and $BA$.
Solution
In this case $A$ and $B$ are both $2 \times 2$ (square) matrices and so we can calculate $AB$ and $BA$. The result of both multiplications will be a $2 \times 2$ matrix. We have
$AB = \pmatrix{0 & \;\;\;4 \\ 1 & -1}\pmatrix{1 & \;\;\;1 \\ 2 & -1} = \pmatrix{\;\;\;8 & -4 \\ -1 & \;\;\;2}$
and
$BA = \pmatrix{1 & \;\;\;1 \\ 2 & -1}\pmatrix{0 & \;\;\;4 \\ 1 & -1} = \pmatrix{\;\;\;1 & 3 \\ -1 & 9}$
Note: This is an example of a very important result in matrix arithmetic. In general, for square matrices $A$ and $B$, we have that $AB \neq BA$.
End of Example 11Example 12
If possible evaluate the following matrix products:
(i). $\pmatrix{\;\;\,1 & 2 & \;\;\,3 \\ \;\;\,2 & 0 & \;\;\,1 \\ -1 & 1 & -1}\pmatrix{\;\;\,1 & 2 \\ \;\;\,4 & 2 \\ -1 & 0}$.
(ii). $\pmatrix{a & b \\ b & a}\pmatrix{1 & 2 \\ 3 & 4}$.
(iii). $\pmatrix{1 & x \\ x & 2}\pmatrix{x & y \\ x & 1}$.
(iv). $\pmatrix{\;\;\,3 \\ -1 \\ \;\;\,2}\pmatrix{2 & 0 & -1 & 6}$
(v). $\pmatrix{2 & 0 & -1 & 6}\pmatrix{\;\;\,3 \\ -1 \\ \;\;\,2}$.
Solution
(i) $\pmatrix{\;\;\,1 & 2 & \;\;\,3 \\ \;\;\,2 & 0 & \;\;\,1 \\ -1 & 1 & -1}\pmatrix{\;\;\,1 & 2 \\ \;\;\,4 & 2 \\ -1 & 0}$.
The product can be formed as the first matrix has size $3 \times 3$ and the second matrix has size $3 \times 2$, i.e. the number of columns in the first matrix $(3)$ is the same as the number of rows $(3)$ in the second matrix. The product matrix will have size $3 \times 2$. Multiplying gives,
$\pmatrix{1 \times 1 + 2 \times 4 + 3 \times (-1) & 1 \times 2 + 2 \times 2 + 3 \times 0 \\ 2 \times 1 + 0 \times 4 + 1 \times (-1) & 2 \times 2 + 0 \times 2 + 1 \times 0 \\-1 \times 1 + 1 \times 4 + (-1) \times (-1) & -1 \times 2 + 1 \times 2 + (-1) \times 0} = \pmatrix{6 & 6 \\ 1 & 4 \\ 4 & 0}$
(ii). $\pmatrix{a+3b & 2a+4b \\ b+3a & 2b+4a}$ (Exercise: Check this answer)
(iii). $\pmatrix{x + x^2 & y + x \\ x^2 + 2x & xy + 2}$ (Exercise: Check this answer)
(iv). $\pmatrix{\;\;\,3 \\ -1 \\ \;\;\,2}\pmatrix{2 & 0 & -1 & 6}$
The product can be formed as the first matrix has size $3 \times 1$ and the second matrix has size $1 \times 4$, i.e. the number of columns in the first matrix $(1)$ is the same as the number of rows $(1)$ in the second matrix. The product matrix will have size $3 \times 4$. Multiplying gives,
$\pmatrix{\;\;\,3 \times 2 & \;\;\,3 \times 0 & \;\;\,3 \times (-1) & \;\;\,3 \times 6 \\ -1 \times 2 & -1 \times 0 & -1 \times (-1) & -1 \times 6 \\ \;\;\,2 \times 2 & \;\;\,2 \times 0 & \;\;\,2 \times (-1) & \;\;\,2 \times 6} = \pmatrix{\;\;\,6 & 0 & -3 & \;\;16 \\ -2 & 0 & \;\;\,1 & -6 \\ \;\;\,4 & 0 & -2 & \;\;12}$
(v). $\pmatrix{2 & 0 & -1 & 6}\pmatrix{\;\;\,3 \\ -1 \\ \;\;\,2}$
The product cannot be formed as the first matrix has size $1 \times 4$ and the second matrix has size $3 \times 1$, i.e. the number of columns in the first matrix $(4)$ is not the same as the number of rows $(3)$ in the second matrix.
End of Example 12Example 13
Evaluate the product $A \underline{x}$ where $A = \pmatrix{4 & \;\;\,2 \\ 3 & -7}$ and $\underline{x} = \pmatrix{x \\ y}$.
Solution
Note that here we are multiplying a $2 \times 2$ matrix and a $2 \times 1$ matrix, i.e. a column vector. The matrices are conformable for matrix multiplication and the result will be a $2 \times 1$ column vector.
Here $A\underline{x} = \pmatrix{4 & \;\;\,2 \\ 3 & -7}\pmatrix{x \\ y} = \pmatrix{4x + 2y \\ 3x - 7y}$.
By multiplying a matrix and a vector we have generated the left hand side of a system of simultaneous linear equations which we encountered in the first unit of this course. In Section 6 we shall see how, under certain conditions, matrix methods can be employed to solve linear systems.
End of Example 13Example 14
Let $A = \pmatrix{1 & 2 & 3 \\ 2 & 5 & 3 \\ 1 & 0 & 8}$ and $B = \pmatrix{-40 & 16 & \;\;\,9 \\ \;\;\,13 & -5 & -3 \\ \;\;\;\;5 & -2 & -1}$. Calculate the matrix products $AB$ and $BA$.
Solution
(i). $AB = \pmatrix{1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1}, BA = \pmatrix{1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1}$
Exercise: You should verify these calculations.
Unlike Example 11 we find that in this case matrix multiplication is commutative and $AB = BA$. This particular square matrix, with 1’s on the main diagonal (top left to bottom right) and 0’s everywhere else, is known as the identity matrix – see Section 5 for further discussions.
End of Example 14Example 15
Determine the values of $x$ and $y$ that satisfy the following matrix equation.
$\pmatrix{1 & \;\;\,3 \\ x & -2}\pmatrix{2 & 4 \\ 3 & y} = \pmatrix{11 & \;\;\,1 \\ \;\;\,6 & 26}$
Solution
Expanding the left-hand-side (LHS) gives,
$\pmatrix{1 & \;\;\,3 \\ x & -2}\pmatrix{2 & 4 \\ 3 & y} = \pmatrix{11 & 4 + 3y \\ 2x - 6 & 4x - 2y} = \pmatrix{11 & \;\;\,1 \\ \;\;\,6 & 26}$
We therefore have three equations. The first two of these are equations in one variable which can easily be solved for $x$ and $y$. The third equation can be used to check our answers.
$ {\array{2x -6 = 6 \\ 4 + 3y = 1 \\ 4x - 2y = 26}}\Bigg\} \implies x = 6,\; y = -1 $.
End of Example 15 -
3.5. Transpose Matrix
The matrix obtained from $A$ by interchanging the rows and the columns of $A$ is called the transpose of $A$ and is denoted $A^T$. We refer to this matrix as, “$A$ transpose”.
Example 16
Let $A = \pmatrix{1 & -2 & 7 \\ 6 & \;\;\,0 & 5}$. Write down the matrix $A^T$.
Solution
The matrix $A^T$ is obtained by interchanging rows and columns of the matrix $A$. Hence,
$A^T = \pmatrix{\;\;\,1 & 6 \\ -2 & 0 \\ \;\;\,7 & 5}$.
Note that Row 1 of $A$ is Column 1 of $A^T$ and Row 2 of $A$ is Column 2 of $A^T$.
Alternatively, Column 1 of $A$ is Row 1 of $A^T$, etc.
End of Example 163.5.1. Properties of transpose matrices
$(A^T)^T = A$ the transpose of a transpose matrix equals the original matrix. $(AB)^T = B^TA^T$ the transpose of a matrix product equals the product of the transpose matrices, with the order of multiplication reversed. $(A + B)^T = A^T + B^T$ the transpose of a matrix sum equals the sum of the transpose matrices. $(k A)^T = kA^T$ the transpose of a matrix multiplied by a scalar equals the scalar multiplied by the transpose of the matrix, $k \neq 0$ is a scalar -
4. Special matrices
There are several special matrices that we should be aware of as they will be needed in future calculations.
4.1. The identity matrix
We know that when any number in multiplied by the number 1 the value of the original number is unchanged, e.g. $1 \times 9 = 9,\;\; 1 \times 100 = 100$, etc.
In this context we call 1 the identity element for multiplication.
We now define an identity element for matrix multiplication so that when a matrix is multiplied by the identity it remains unchanged. This identity element is called an identity matrix and is only defined for square matrices. Although there is only a single multiplicative identity, i.e. 1, when working with numbers there are many different identity matrices depending on the size of the matrix in question, e.g. $2 \times 2,\;\; 3 \times 3$, etc.
The identity matrix has 1 on the main diagonal (the diagonal starting at top left and going to bottom right) and zeros everywhere else – see Example 14. The matrix is usually represented by $I$. Note that some textbooks include a subscript $n$, and write $I_n$, to indicate the size of the identity matrix.
Example 17
(i). The $2 \times 2$ identity matrix is, $I = \pmatrix{1 & 0 \\ 0 & 1}$.
(ii). We met the $3 \times 3$ identity matrix, $I = \pmatrix{1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1}$ in Example 14.
End of Example 174.2. The zero matrix
The zero matrix is a matrix for which every element is zero. Strictly speaking there are many zero matrices, one for each possible size of matrix. Here are the $2 \times 2$ and $2 \times 4$ zero matrices.
$\pmatrix{0 & 0 \\ 0 & 0}$$\pmatrix{0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0}$
The zero matrix is the identity matrix for matrix addition as shown in the following example.
Example 18
If $A = \pmatrix{\;\;\,1 & 9 \\ -2 & 3}$ then
$\pmatrix{\;\;\,1 & 9 \\ -2 & 3} + \pmatrix{0 & 0 \\ 0 & 0} = \pmatrix{\;\;\,1 & 9 \\ -2 & 3}$
The matrix $A$ is unchanged by addition of the zero matrix.
End of Example 184.3. Diagonal matrices
A square matrix is called a diagonal matrix if all the entries that do not lie on the main diagonal are zero. Note that it is allowed for some entries on the main diagonal to equal zero.
Example 19
The following matrices are all examples of diagonal matrices:
(i). $\pmatrix{6 & \;\;\,0 \\ 0 & -1} $ (ii). $\pmatrix{2 & \;\;\,0 & 0 \\ 0 & -5 & 0 \\0 & \;\;\,0 & 3}$(iii). $\pmatrix{4 & 0 & \;\;\,0 \\ 0 & 0 & \;\;\,0 \\0 & 0 & -1}$.
The identity matrix, see Example 17 is a special case of a diagonal matrix where all the diagonal entries are equal to 1.
End of Example 194.4. Symmetric matrices
A square matrix is called a symmetric matrix if it is equal to its own transpose, i.e. $A = A^T$.
Example 20
The following matrices are all symmetric,
(i). $\pmatrix{\;\;\,3 & -1 \\ -1 & \;\;\,3}$ (ii). $\pmatrix{2 & \;\;\,0 & 1 \\ 0 & -6 & 3 \\ 1 & \;\;\,3 & 5}$(iii). $\pmatrix{3 & \;\;\,2 & \;\;\,1 \\ 2 & -9 & -3 \\ 1 & -3 & \;\;\,4}$
End of Example 20 -
Summary
- In this unit we introduced matrices and you should now be able to:
- perform basic matrix arithmetic including addition, subtraction and scalar multiplication.
- determine whether matrices are conformable for matrix multiplication.
- carry out matrix multiplication where appropriate.
- determine the transpose of a matrix.
- identify special matrices including: identity, diagonal and symmetric matrices.
You are now ready to attempt the multiple choice exercise at the link below.
You should now attempt the tutorial exercises on GCU Learn.
In the next unit we look at calculating the inverse of a $2 \times 2$ matrix and present some real-world applications of matrices.