08
-

-
Lecture 8 - Discrete Uniform Distribution, Bernoulli Trials, Binomial Distribution
- Discrete Uniform Distribution,
Bernoulli Trials,
Binomial Distribution - Discrete Uniform Distribution,
-
Discrete Uniform Distribution
- If the random variable X assumes the values x1, x2,…, xn, with equal probabilities, then the discrete uniform distribution is given by f(xi) = 1/n for i=1,2,…,n
- This result can easily be obtained from the fact that n equal numbers (probabilities) add up to one due to unitary property. Each number is then equal to 1/n.
Expected value and variance of die toss
- Let X be the number obtained by a fair die toss.
- Find E[X], Var[X] and standard deviation of X.
Expected value
- From formula for expected value: μ = E[X] = ∑k xkf(xk)
E[X]=1/6(1+2+3+4+5+6)=21/6=7/2=3.5- Intuitively, 3.5 is the “middle” point of possible outcome values: 1,2,3,3.5,4,5,6
Variance and standard deviation
- From formula for variance: σ2 = Var[X] = ∑k (xk − μ)2f(xk) =E[X2]- μ2
- Var[X]=1/6(1+4+9+16+25+36)-49/4=
91/6-49/4=(182-147)/12=35/12- Std. dev= σ=sqrt(35/12)
Discrete Uniform Distribution Over A Given Range
- Let X be a discrete uniform random variable ranging from a,a+1,a+2,…,b, for a ≤ b.
There are b – (a-1) values in this range (why?). Therefore: f(x) = 1/(b-a+1) for x=a,…,b- Mean μ and variance σ2 of discrete uniform random variable X are:
μ = (b+a)/2
σ2 = [(b-a+1)2–1]/12 -
Bernoulli Trials
- Bernoulli trial is a random experiment with exactly two possible outcomes, "success" and "failure“
- Named after Swiss mathematician Jacob Bernoulli
- If a certain event A occurs, we call it ‘success’ and its probability is denoted as P(A) = p.
Then the probability of ‘failure’ P(A’) becomes q = 1− p.
Remember that A’ denotes the complement of A
- Examples: tossing a coin, observing bits in digital communication, looking for faulty product, service outage…
Multiple Bernoulli Trials
- Q: What happens when several Bernoulli trials are performed?
A: binomial experiment! Binomial experiment consists of a fixed number n of independent Bernoulli trials, each with a probability of success p, and it counts the number of successes
Distribution of successes of binomial experiment is called binomial distribution
Binomial Distribution
- The random variable X that equals the number of trials which result in a success is a binomial random variable with parameters 0 < p < 1 and n = 1, 2, ....
The probability mass function for k successes out of n trials is:
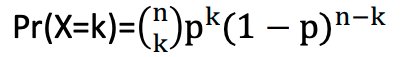
- The name binomial comes from the binomial expansion: for constants x and y, the binomial expansion is
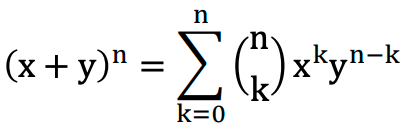
- Bernoulli trial is a random experiment with exactly two possible outcomes, "success" and "failure“
-
Mean and Variance of Binomial Distribution
- If X is a binomial random variable with parameters p and n, then the mean μ and variance σ2 are given as follows:
μ = E[X] = np
σ2 = V[X] = np(1-p)
Example with Binomial Distribution
- Digital communication channel has an error probability Pe (i.e., the probability of receiving 0 when 1 is transmitted, or vice versa, is Pe).
A sequence of n binary digits is transmitted over this channel.
- a) Determine the probability of receiving exactly k digits in error assuming each received digit is independent of others.
- b) If Pe = 10^(−5), determine the probability of receiving 2 digits in error in a sequence of 8 binary digits.
- c) Since we are looking for number of successes, k, in n independent trials, this is straightforward application of binomial distribution.
Note: p = Pe (‘success’ here is receiving a digit in error), so that we have
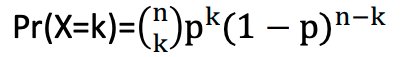
- If Pe = 10^(−5), k = 2 and n = 8, and since p=Pe, we have that probability of having two erroneous digits out of 8 is:
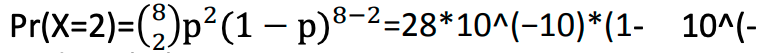
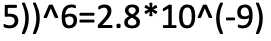
- d) If Pe = 10^(−5), determine the probability of receiving at most 2 digits in error in a sequence of 8 binary digits.
- Solution: At most 2 errors implies we can have three cases: 0, 1 or 2 errors. We also recall that p=Pe.
Thus, we obtain the probability of receiving at most 2 digits in error in a sequence of 8 binary digits by summing the individual probabilities of those three cases:
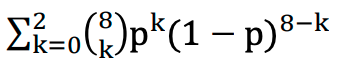
- If X is a binomial random variable with parameters p and n, then the mean μ and variance σ2 are given as follows:
- Insert Content Here 6
- Insert Content Here 7