-
Matrices
In this unit we continue with our work on matrices. We describe how to calculate the determinant of a $2 \times 2$ matrix and introduce the condition for the existence of an inverse matrix. A formula for calculating the inverse of a $2 \times 2$ matrix is presented supported by examples. Some applications of matrices in the real-world are then given, including solving linear systems of algebraic equations, computer graphics, cryptography and the modelling of graphs and networks
If required further resources on determinants and inverse matrices can be found at:
-
5. The determinant and inverse of a $2 × 2$ matrix
Consider the following arithmetic evaluations for numbers,
$ \matrix{2 \times 2^{-1}=2^{-1} \times 2 = 1 \\ 3 \times 3^{-1} = 3^{-1} \times 3 = 1 \\ 4 \times 4^{-1} = 4^{-1} \times 4 = 1 \\ ......................\\ a \times a^{-1} = a^{-1} \times a = 1 \\ .....................}$
One way of interpreting the above is that any (non-zero) number $a$ has associated with it a multiplicative inverse $a^{-1}$. Furthermore, any number multiplied by its inverse equals 1, the multiplicative identity for scalars.
We can make an analogous statement for (some) square matrices that will prove useful later.
In this module we restrict our work to calculating inverses of $2 \times 2$ matrices.
For a general $2 \times 2$ matrix, $A = \pmatrix{a & b \\ c & d}$ provided
$det(A) = ad - bc \neq 0$
there exists another $2 \times 2$ matrix, called the inverse of $A$, denoted $A^{-1}$, where
$A^{-1} = \frac{1}{det(A)}\pmatrix{\;\;\,d & -b \\ -c & \;\;\,a}$.
The quantity $det(A)$ is called the determinant of $A$ and is often written, $\mid A \mid$ .
The determinant of a matrix can therefore be used to determine the existence (or otherwise) of a matrix inverse by checking that it is non-zero.
In a manner similar to that observed earlier for scalars,
$AA^{-1} = A^{-1}A = I$
where $I$ is the identity matrix with the same size as $A$. Also,
$AI = IA = A$.
Note that $A^{-1}$ must not be interpreted as $1/A$.
A matrix with an inverse is called invertible or non-singular.
A matrix with no inverse is said to be non-invertible or singular.
We now look at how to determine inverse matrices, where they exist, for the $2 \times 2$ case.
Example 21
Calculate the determinant of each of the following matrices. Hence, identify which matrices are invertible and for each invertible matrix calculate its inverse.
(i). $A = \pmatrix{\;\;\,2 & -1 \\ -2 & \;\;\,1}$ (ii). $B = \pmatrix{7 & 3 \\ 2 & 1}$
(iii). $C = \pmatrix{0 & 1 \\ 0 & 1}$ (iv). $M = \pmatrix{\;\;\,2 & \;\;\,0 \\ -2 & -3}$
Solution
(i). $det(A) = 2 \times 1 - (-1) \times (-2) = 2 - 2 = 0$. No Inverse.
(ii). $det(B) = 7 \times 1 - 3 \times 2 = 7 - 6 = 1 \neq 0$. Matrix has an inverse.
$B^{-1} = \ {\Large\frac{1}{1}}\pmatrix{\;\;\,1 & -3 \\ -2 & \;\;\,7}$
$=\pmatrix{\;\;\,1 & -3 \\ -2 & \;\;\,7}$
Exercise: Check that $BB^{-1} = B^{-1}B = I$ .
(iii). $det(C) = 0 \times 1 - 1 \times 0 = 0 - 0 = 0$. No inverse.
(iv). $det(M) = 2 \times (-3) - 0 \times (-2) = -6 \neq 0$.
$M^{-1} = -{\Large\frac{1}{6}}\pmatrix{-3 & 0 \\ \;\;\,2 & 2}$
$= {\Large\frac{1}{6}}\pmatrix{\;\;\,3 & \;\;\,0 \\ -2 & -2}$
Exercise: Check that $MM^{-1} = M^{-1}M = I$.
The calculation of inverses for square matrices larger than $2 \times 2$ is considerably more involved and is beyond the scope of this course.
End of Example 21Example 22
If $A = \pmatrix{a & b \\ c & d}$ and $ad - bc \neq 0$ show that $AA^{-1} = I$.
Solution
$AA^{-1} = {\Large\frac{1}{ad - bc}}\pmatrix{a & b \\c & d}\pmatrix{\;\;\,d & -b \\ -c & \;\;\,a}$
$= {\Large\frac{1}{ad - bc}}\pmatrix{ad-bc & -ab+ba \\ cd-dc & \;\;\,ad-bc}$
$= {\Large\frac{1}{ad - bc}}\pmatrix{ad-bc & \;\;0 \\ \;\;0 & ad-bc}$
$= \pmatrix{1 & 0 \\ 0 & 1} = I$ as required.
End of Example 22Example 23
Consider the matrix equation
$\pmatrix{2 & \;\;6 \\ 4 & 10}\pmatrix{a & b \\ c & d} = \pmatrix{4 & 8 \\ 0 & 4}$.
Determine the values of $a, b, c$ and $d$.
Solution
let $A = \pmatrix{2 & \;\;6 \\ 4 & 10}$. Determine $A^{-1}$ and multiply both sides of the equation by $A^{-1}$.
Here $A^{-1} = -{\Large\frac{1}{4}}\pmatrix{\,10 & -6 \\ -4 & \;\;\,2} = {\Large\frac{1}{4}}\pmatrix{-10 & \;\;\;6 \\ \;\;\;4 & -2}$ and so we have
$\pmatrix{a & b \\ c & d} = {\Large\frac{1}{4}}\pmatrix{-10 & \;\;\,6 \\ \;\;\,4 & -2}\pmatrix{4 & 8 \\ 0 & 4}$
$= {\Large\frac{1}{4}}\pmatrix{-40 & -56 \\ \;\;\,16 & \;\;\,24}$
$= \pmatrix{-10 & -14 \\ \;\;\;4 & \;\;\;6}$
Hence, $=\;$ $a=-10$, $b=-14$, $c=4$, $d=6$.
Exercise: An alternative approach involves expanding the matrix equation to obtain a system of simultaneous equations. Use this method to verify the above results.
End of Example 235.1. Properties of inverse matrices
If $A$ and $B$ are invertible matrices:
$(A^{-1})^{-1} = A$ the inverse of an inverse matrix equals the original matrix. $(AB)^{-1} = B^{-1}A^{-1}$ the inverse of a matrix product equals the product of the inverse matrices, with the order of multiplication reversed. $(kA)^{-1} = \frac{1}{k}A^{-1}$ the inverse of a matrix multiplied by a scalar equals the inverse of the scalar multiplied by the inverse of the matrix, $k \neq 0$ is a scalar. $(A^T)^{-1} = (A^{-1})^T$ the inverse of a transpose matrix equals the transpose of the inverse matrix. -
6. Applications of matrices
Now that we have familiarised ourselves with the basic definitions and operations of matrices we can turn our attention to looking at some applications where matrices are used to model real-world problems.
6.1. Solving systems of simultaneous equations by matrix methods
If required further resources on the topic can be found at:
In the opening unit of the module we looked at two methods (elimination and substitution) for solving simultaneous linear algebraic equations. We shall now look at a third method using matrices that lays the foundation for tackling large systems with many equations.
In dealing with simultaneous equations, we normally require as many equations as there are unknowns, e.g. 2 equations in 2 unknowns, 3 equations in 3 unknowns, and so on. For example, a system of $n$ equations in $n$ unknowns is given by
$a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n = b_1 \\ a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n = b_2 \\ ............................... \\ ............................... \\ a_{n1}x_1 + a_{n2}x_2 + \cdots + a_{nn}x_n = b_n$
This system can be written as a matrix equation of the form
$A\underline{x} = \underline{b}$
- where
- $\underline{x}$ is a column vector whose components are the unknowns in the equations.
- $A$ is a square matrix $(n \times n)$ whose elements are the coefficients of the unknowns.
- $\underline{b}$ is a column vector of the equation constants, i.e. known right-hand-side values.
We therefore have
$A = \pmatrix{a_{11} & a_{12} & \cdots & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & \cdots & a_{2n} \\ \vdots & & \ddots & & \vdots \\ \vdots & & & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & \cdots & a_{nn}}, \underline{x} = \pmatrix{x_1 \\ x_2 \\ \vdots \\ \vdots \\ x_n}, \underline{b} = \pmatrix{b_1 \\ b_2 \\ \vdots \\ \vdots \\ b_n}$.
Provided $A$ is invertible, i.e. $det(A) \neq 0$, the system has a unique solution.
The solution of the matrix equation is the vector $\underline{x}$ and the elements of $\underline{x}$ give the solution of the simultaneous equations.
To find $\underline{x}$, provided the coefficient matrix $A$ is invertible, we pre-multiply both sides of the matrix equation by the inverse of $A$ and simplify. We have
$A\underline{x} = \underline{b}$
$A^{-1}A\underline{x} = A^{-1}\underline{b}$
$I\underline{x} = A^{-1}\underline{b}$
$\underline{x} = A^{-1}\underline{b}$
For comparison, an analogous procedure for a scalar equation is given below.
$a x = b$
$a^{-1}a x = a^{-1}b$
$1x = a^{-1}b$
$x = a^{-1}b$.
We now return to Example 18 in Unit 1 and apply matrix methods to obtain a solution. This problem was previously solved using the methods of substitution and elimination.
Example 24
(i). Solve the system of simultaneous equations
$x + 2y = -1$
$4x - 3y = 18$
using matrix methods.
Solution
First write the equations in the matrix form, $A \underline{x} = \underline{b}$:
$\pmatrix{1 & \;\;\,2 \\ 4 & -3}\pmatrix{x \\ y} = \pmatrix{-1 \\ 18}$
Calculate $A^{-1}$ if it exists.
$det(A) = 1 \times (-3) - 2 \times 4 = -11 \neq 0$ and so the matrix is invertible.
Hence,
$A^{-1} = -{\Large\frac{1}{11}}\pmatrix{-3 & -2 \\ -4 & \;\;\,1} = {\Large\frac{1}{11}}\pmatrix{3 & \;\;\,2 \\ 4 & -1}$
Now solve the system by forming, $\underline{x} = A^{-1} \underline{b}$.
$\pmatrix{x \\ y} = {\Large\frac{1}{11}}\pmatrix{3 & \;\;\,2 \\ 4 & -1}\pmatrix{-1 \\ \;18} = {\Large\frac{1}{11}}\pmatrix{\;\;\,33 \\ -22} = \pmatrix{\;\;\,3 \\ -2}$
Hence, $x=3$ and $y=-2$ as we obtained in Unit 1.
(ii). Solve the system of simultaneous equations
$4x + 2y = 10$
$3x - 7y = -1$
using matrix methods.
Solution
First write the equations in the matrix form, $A \underline{x} = \underline{b}$:
$\pmatrix{4 & \;\;\,2 \\ 3 & -7}\pmatrix{x \\ y} = \pmatrix{\;\;10 \\ -1}$
Calculate $A^{-1}$ if it exists.
$det(A) = -28 - 6 = -34 \neq 0$ and so the matrix is invertible.
Hence,
$A^{-1} = -{\Large\frac{1}{34}}\pmatrix{-7 & -2 \\ -3 & \;\;\,4} = {\Large\frac{1}{34}}\pmatrix{7 & \;\;\,2 \\ 3 & -4}$
Now solve the system by forming, $\underline{x} = A^{-1}\underline{b}$.
$\pmatrix{x \\ y}={\Large\frac{1}{34}}\pmatrix{7 & \;\;\,2 \\ 3 & -4}\pmatrix{\;\;10 \\ -1}= {\Large\frac{1}{34}}\pmatrix{68 \\ 34} = \pmatrix{2 \\ 1}$
Hence, $x=2$ and $y=1$.
End of Example 24Example 25
A system of two simultaneous equations is given by
$3x + 5y = 8$
$7x - 4y = 50$
(i). Express these simultaneous equations in the form
$A\underline{x} = \underline{b}$
where $A$ is a $2 \times 2$ matrix, $\underline{b}$ is a $2 \times 1$ matrix and $\underline{x} = \pmatrix{x \\ y}$.
(ii). Determine the inverse of $A$.
(iii). Hence, solve the system of simultaneous equations.
Solution
(i). In matrix form we have, $\pmatrix{3 & \;\;\,5 \\ 7 & -4}\pmatrix{x \\ y} = \pmatrix{\;\;\,8 \\ 50}$
(ii). $det(A) = -12 - 35 = -47 \neq 0$ and so $A^{-1}$ exists.
$A^{-1} = -\frac{1}{47}\pmatrix{-4 & -5 \\ -7 & \;\;\,3} = \frac{1}{47}\pmatrix{4 & \;\;\,5 \\ 7 & -3}$
(iii). $\underline{x} = A^{-1}\underline{b}$
$\pmatrix{x \\ y} = \frac{1}{47}\pmatrix{4 & \;\;\,5 \\ 7 & -3}\pmatrix{\;\,8 \\ 50} = \frac{1}{47}\pmatrix{\;282 \\ -94} = \pmatrix{\;\;\,6 \\ -2}$
$x=6$,$y=-2$
End of Example 25Note: Recall that in the opening unit, when we looked at a system of two linear equations in two unknowns, we found that there were three cases to consider:
(i). the system has a unique solution (independent equations)
(ii). the system has no solution (inconsistent equations)
(iii). the system has infinitely many solutions (dependent equations).
In terms of matrices the first case corresponds to the determinant of the coefficient matrix being non-zero, as in the examples above. The other two cases are associated with a zero determinant and need further investigation. We do not address these cases in this module.
In general, we can solve $2 \times 2$ systems using elimination or substitution with about the same amount of effort as for matrix methods. It is when the systems of equations become larger that matrix methods really come into their own. Elimination and substitution methods are not feasible for large systems but matrix methods can easily be programmed on a computer and can be extremely efficient.
-
6.2. Matrices and cryptography
Cryptography is essentially concerned with concealing information from all those that are not entitled to access it. A plaintext message is encrypted, using a chosen cipher, and the resulting ciphertext transmitted to the receiver who is able to decrypt the ciphertext and retrieve the original plaintext. Of particular interest here is that a matrix can be used as a cipher to encrypt a message. In this context the matrix is often referred to as a key matrix.
A further application of matrices in cryptography addresses the problem of encrypted messages being corrupted during transmission. Parity check matrices are used to detect and, in some cases, correct the errors.
6.2.1. Encoding a PIN number
As a simple example of an application of matrix multiplication in cryptography we consider the case of encoding a four digit PIN number, before sending it over an ‘open’ line.
Given a four digit PIN number, $abcd$, we can record this in a matrix in a column-wise manner as,
$P = \pmatrix{a & c \\ b & d}$.
To encrypt the PIN we multiply the matrix $P$ by an invertible coding (key) matrix, $E$, known only to the sender and receiver. The receiver can then decrypt the information using $E^{-1}$ , as he/she knows the encoding matrix, $E$.
Example 26
Suppose we want to encode the four digit PIN: $1 0 4 9$.
Record this information in a $2 \times 2$ matrix $P$ as, $P = \pmatrix{1 & 4 \\ 0 & 9}$.
Encode the PIN by multiplying $P$ on the left by a key matrix $E$ where, say, $E = \pmatrix{3 & 1 \\ 2 & 1}$
The matrix $C$, containing the enciphered PIN, is then
$C = EP = \pmatrix{3 & 1 \\ 2 & 1}\pmatrix{1 & 4 \\ 0 & 9} = \pmatrix{3 & 21 \\ 2 & 17}$.
The sender transmits this information to the receiver who knows the coding matrix $E$.
To decipher the coded PIN the receiver uses the inverse of the matrix $E$, i.e.
$E^{-1} = \pmatrix{\;\;\,1 & -1 \\ -2 & \;\;\,3}$
Then
$E^{-1}C = \pmatrix{\;\;\,1 & -1 \\ -2 & \;\;\,3}\pmatrix{3 & 21 \\ 2 & 17} = \pmatrix{1 & 4 \\ 0 & 9} = P$
This approach works since
$E^{-1}C = E^{-1}EP = IP = P$.
End of Example 266.2.2. Substitution ciphers
In a substitution cipher we represent each letter of the alphabet by the number which corresponds to that letter's position in the alphabet, starting with A at position zero. Hence, A is represented by 0, B is represented by 1 and so on up to Z which is represented by 25. The look-up table below shows the letter/number correspondences for the English alphabet.
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 The Hill Cipher (OPTIONAL)
The Hill cipher, incvented by Lester Hill in 1929, is an example of a polygraphic substitution cipher. Application of the Hill cipher requires knowledge of modular arithmetic, a topic we shall meet later in the module. This example is for illustration purposes and is therefore optional.
Note: In modulo $m$ arithmetic all integers are replaced by their remainders after division by $m$. For example, in modulo 26 arithmetic the number 57 is divided by 26 giving the remainder 5.
The Hill cipher has as its key a square matrix operating with modular arithmetic. The message is broken down into blocks and these blocks are converted into (column) vectors. The enciphering process involves multiplying each vector by the matrix.
Example 27
A message is converted into numeric form by defining,
$A = 0, B = 1, .... , Y = 24, Z = 25$.
The message is then encrypted using the matrix
$E = \pmatrix{1 & 2 \\ 4 & 3}$.
Determine the ciphertext that represents encryption of the message, CODE.
Solution
From the look-up table we find that the word CODE is represented numerically by
$2, \;\;\; 14, \;\;\; 3, \;\;\; 4. $
Divide into blocks of length 2 giving the column vectors $\pmatrix{\;\,2 \\ 14}$ and $\pmatrix{3 \\ 4}$.
To simplify subsequent calculations we form a matrix, $P$, whose columns consist of these vectors,
$P = \pmatrix{\;\,2 & 3 \\ 14 & 4}$
Encrypt the message by multiplying $P$ on the left by the encryption matrix $E$. Note that we could equally well multiply $P$ on the right by $E$ to obtain a different ciphertext.
The matrix $C$ containing the numerical values corresponding to the ciphertext for the word CODE is then
$C = EP = \pmatrix{1 & 2 \\ 4 & 3}\pmatrix{\;\,2 & 3 \\ 14 & 4} = \pmatrix{30 & 11 \\ 50 & 24 }$
Reading the values from $C$ we have,
$30 \;\;\; 50 \;\;\; 11 \;\;\; 24$.
Operating modulo 26, these values become, $4 \;\; 24 \;\; 11 \;\; 24$.
From the look-up table given above the ciphertext for the message CODE is, EYLY.
Note: To decrypt a ciphertext, constructed using a Hill cipher, we use the inverse matrix $E^{-1}$ operating with modular arithmetic.
End of Example 276.2.3. Parity Check matrices (NON-EXAMINABLE)
During the transmission phase a codeword can undergo bit corruption due to, for example, electromagnetic interference. Parity check matrices, derived from parity check equations, enable the validity of a received codeword to be checked. In short the codeword is treated as a vector and is multiplied by a parity check matrix to produce a vector called an error syndrome. The parity check process has the property that it maps valid codewords to the zero vector and non-valid codewords to a non-zero vector. In some cases the detected errors can be corrected.
Example 28
Use the binary parity check matrix
$H = \pmatrix{1 & 1 & 0 & 1 & 0 & 0 \\ 0 & 1 & 1 & 0 & 1 & 0 \\ 1 & 0 & 1 & 0 & 0 & 1}$
to calculate the error syndrome associated with the vectors
$\pmatrix{1 & 1 & 1 & 0 & 0 & 0}^T$ and $\pmatrix{0 & 1 & 1 & 1 & 1 & 0}^T$.
Hence, identify which of the two is a valid codeword as recognised by the parity check.
Note that this example is for illustration purposes and is therefore optional.
Solution
As we have a binary check matrix we operate modulo 2, i.e.
$\pmatrix{1 & 1 & 0 & 1 & 0 & 0 \\0 & 1 & 1 & 0 & 1 & 0 \\ 1 & 0 & 1 & 0 & 0 & 1}\pmatrix{1 \\ 1 \\ 1 \\ 0 \\ 0 \\ 0} = \pmatrix{0 \\ 0 \\ 0}$
and $\pmatrix{1 & 1 & 0 & 1 & 0 & 0 \\ 0 & 1 & 1 & 0 & 1 & 0 \\ 1 & 0 & 1 & 0 & 0 & 1}\pmatrix{0 \\ 1 \\ 1 \\ 1 \\ 1 \\ 0} = \pmatrix{0 \\ 1 \\ 1}$.
The first is a valid codeword since it multiplies to the zero vector.
End of Example 28 -
6.3. Matrices in computer graphics
In computer graphics we are often required to alter the orientation, position and size of objects by transforming the coordinates of the object. We can obtain these transformations by using vectors and matrices to perform sequences of translations, scalings, rotations and reflections. For illustration purposes we show how reflections and rotations in 2-D can be represented by matrices.
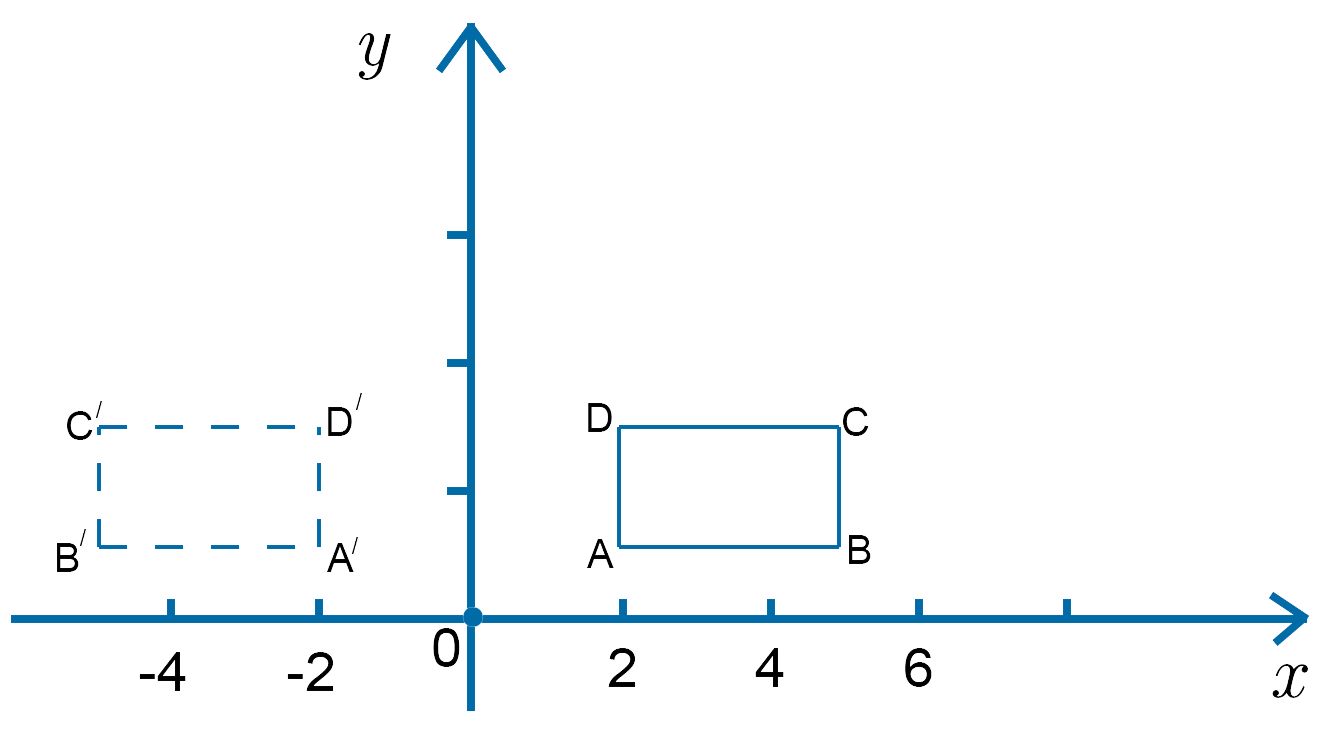
Example 29
A rectangle has its vertices at the points $A(2, 1)$, $B(5, 1)$, $C(5, 3)$ and $D(2, 3)$. Find the coordinates of the image of the rectangle when it is reflected in the line $x = 0$, i.e. the $y$-axis.
Solution
The matrix for a reflection in the line $x = 0$ is given by
$Q = \pmatrix{-1 & 0 \\ \;\;\,0 & 1}$.
(Note that derivation of the reflection matrix is beyond the scope of this course).
We now form a matrix $M$, say, from the coordinates of the rectangle, i.e.
$M = \pmatrix{2 & 5 & 5 & 2 \\ 1 & 1 & 3 & 3}$
Next evaluate the product of the reflection and coordinate matrices as,
$QM = \pmatrix{-1 & 0 \\ \;\;\,0 & 1}\pmatrix{2 & 5 & 5 & 2 \\ 1 & 1 & 3 & 3} = \pmatrix{-2 & -5 & -5 & -2 \\ \;\;\,1 & \;\;\,1 & \;\;\,3 & \;\;\,3}$
The resulting matrix gives the coordinates of the reflected rectangle which is shown in the diagram. Note that these coordinates appear in the same order as they do in the original matrix so, for example, the point $A(2, 1)$ is mapped to the point $A^{'}(-2, 1)$ , etc.
 End of Example 29
End of Example 29Example 30
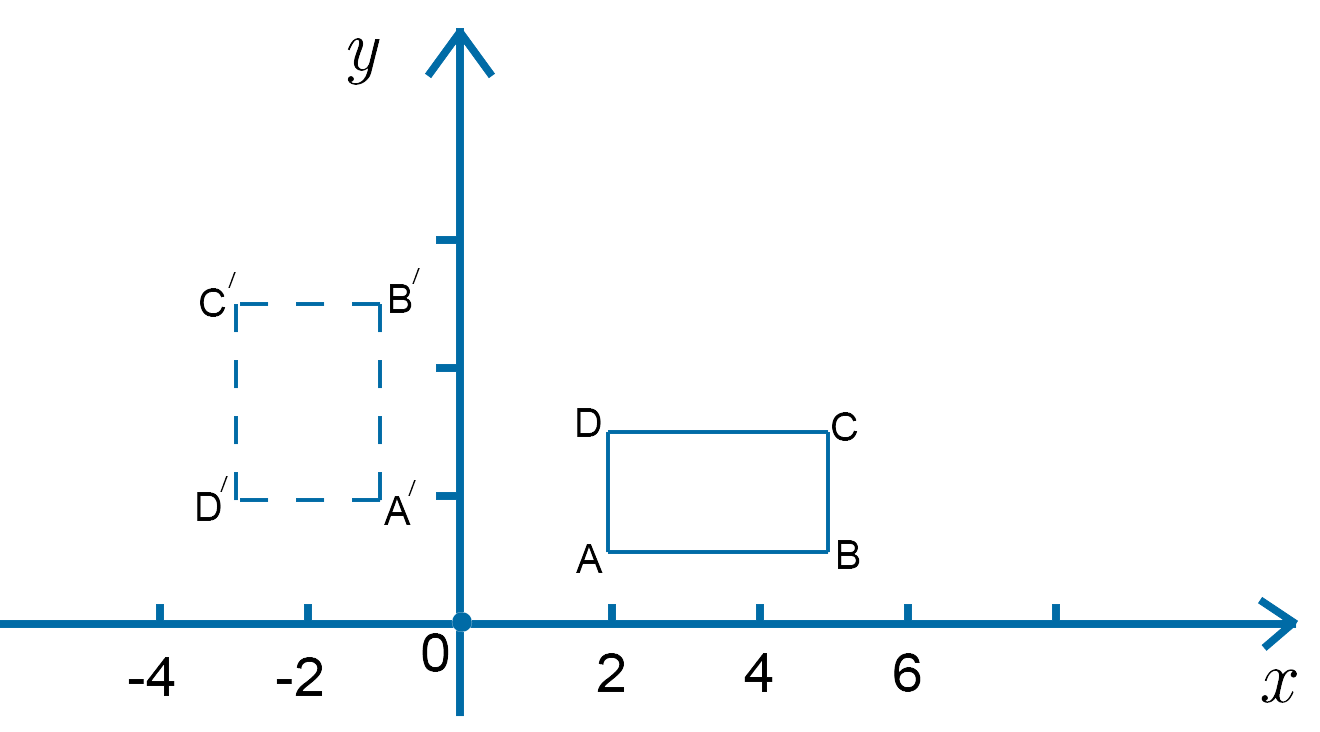
A rectangle has its vertices at the points $A(2, 1)$, $B(5, 1)$, $C(5, 3)$ and $D(2, 3)$. Find the coordinates of the image of the rectangle when it is rotated through 900 anticlockwise about the origin.
Solution
The matrix for a 900 anticlockwise rotation about the origin is given by
$R = \pmatrix{0 & -1 \\ 1 & \;\;\,0}$.
(Note that derivation of the rotation matrix is beyond the scope of this course).
We now form a matrix $M$, say, from the coordinates of the rectangle, i.e.
$M = \pmatrix{2 & 5 & 5 & 2 \\ 1 & 1 & 3 & 3}$.
Now evaluate the product of the rotation and coordinate matrices as,
$RM = \pmatrix{0 & -1 \\ 1 & \;\;\,0}\pmatrix{2 & 5 & 5 & 2 \\ 1 & 1 & 3 & 3} = \pmatrix{-1 & -1 & -3 & -3 \\ \;\;\,2 & \;\;\,5 & \;\;\,5 & \;\;\,2}$.
The resulting matrix gives the coordinates of the vertices of the rotated rectangle which is shown in the diagram. Note that these coordinates appear in the same order as they do in the original matrix so, for example, the point $A(2, 1)$ is mapped to the point $A^{'} (-1, 2)$ , etc.
 End of Example 30
End of Example 306.4. Matrices for modelling graphs and networks
In a later unit we take an introductory look at graph theory, a topic that has in recent years become of significant interest in mathematics and computer science. We note here that in the current context the word graph is not related to the graph of a function, rather how objects are connected to each other. Some of the applications of graph theory include the design of communication networks, modelling of the worldwide web and designing airline route maps.
Example 31
Consider the following graph which shows the number of direct flights per day, regardless of direction, between four cities $P$, $Q$, $R$ and $S$. The cities are represented by nodes and any two cities that are connected by a direct flight are connected by a line called an edge. For example, there are two flights per day between $P$ and $S$ but no daily direct flights between $S$ and $R$.
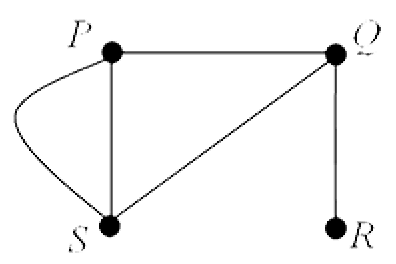
There are a number of ways to represent the information in this graph on a computer, including forming an edge list, or an adjacency list or, of particular interest here, an adjacency matrix. Each method has advantages and disadvantages as regards demands on computing memory and runtime. We briefly look at the adjacency matrix approach which employs a matrix to record whether or not nodes are connected to each other.
If $G$ is a graph with $n$ vertices its adjacency matrix, $A$ is defined as the $n \times n$ matrix whose $ij$-th entry is the number of edges joining node $i$ and node $j$.
- As our graph contains four nodes we will have a $4 \times 4$ adjacency matrix with the first row, corresponding to node $P$, being constructed as follows:
- 0 edges connect node $P$ to node $P$, so the entry in Row1/Column1 is a ‘0’
- 1 edge connects node $P$ to node $Q$, so the entry in Row1/Column2 is a ‘1’
- 0 edges connect node $P$ to node $R$, so the entry in Row1/Column3 is a ‘0’
- 2 edges connect node $P$ to node $S$, so the entry in Row1/Column4 is a ‘2’
Continuing in this way, for each node in turn, we obtain the following adjacency matrix:
$\matrix{P \;\; Q \;\;\, R \;\;\; S}$
$A = \matrix{P \\ Q \\ R \\ S}\pmatrix{0 & 1 & 0 & 2 \\1 & 0 & 1 & 1 \\0 & 1 & 0 & 0 \\2 & 1 & 0 & 0}$.
It can be seen that $A$ is a symmetric matrix.
Note that when the number of edges and nodes in a graph are small, as was the case here, it is relatively easy to show relationships in graphical form. However, as graphs become large it is no longer feasible to display them visually and so options like an adjacency matrix are invaluable.
End of Example 31 -
Summary
- In this unit we have completed our introduction to matrices and you should now be able to:
- calculate the determinant of a $2 \times 2$ matrix.
- know the condition for the existence of an inverse matrix.
- calculate the inverse of a $2 \times 2$ matrix.
- apply matrix methods to solve a system of linear equations in two unknowns.
- use matrices to encode plaintext messages and to decode ciphertext.
- appreciate the application of matrices to real-world problems.
You should now attempt the tutorial exercises and Maple questions on GCU Learn
The next unit introduces basic set theory and the properties of sets.