• Lecture 1 – Poisson Distribution, Gaussian Distribution, z-score


    How horse kicks in Prussian army influenced statistics (Poisson Distribution)

    Gaussian Distribution (binomial and Poission can be approximated with Gaussian distribution)

    z-score

  • Poisson Distribution


    The Poisson distribution is popular for modelling the number of times an event occurs in an interval of time or space.
    Named after French mathematician Siméon Poisson.
    The Poisson random variable X with parameter λ > 0 which equals the average number of events in an interval is given by the probability mass function:

    math representation of poisson distribution

    Parameter λ is also known as a rate parameter


    Poisson Distribution: Mean and Variance


    For the Poisson random variable X with a rate
    parameter λ, the mean is
    μ = E[X] = λ
    and variance is
    σ2=V[X] = λ
    The mean and variance of the Poisson random variable are the same!


    Poisson Distribution: history and applications


    Ladislaus Bortkiewicz published a book at the end of the 19th century which contained data about the number of soldiers killed by being kicked by a horse each year for several Prussian cavalry corps.

    Author showed that the data followed Poisson distribution and, more generally, that events with low frequency in a large population tend to follow a Poisson distribution which hugely popularised use of the distribution

    Photon counting, reliability engineering, number of phone calls, number of customers are some of phenomena modelled with Poisson


    Example: Poisson distribution


    Assume the number of customers follows a Poisson distribution with a mean of 17 customer per day. Find the probabilities of having exactly 10 and 17 customers in one day.


    Click here for solution


    Example: Poisson distribution (2)


    Assume the number of customers follows a Poisson distribution with a mean of 17 customer per day. Find the probabilities of having at least one customer.


    Click here for solution 2

    Solution


    Answer:

    Let X denote the number of customers in a day.
    P(X=10)= e−17 1710/10! =0.023
    P(X=17)= e−17 1717/17! =0.0963

    Solution


    Answer: P(X>0)=?
    Remember: f(x)= e−λ λx/x! for x=0,1,2,…
    P(X>0)= e−17 17 /1! + e−17 172/2! +…
    But this is infinite summation!
    Complement: P(X>0)= 1-P(X=0)= 1 − e−17

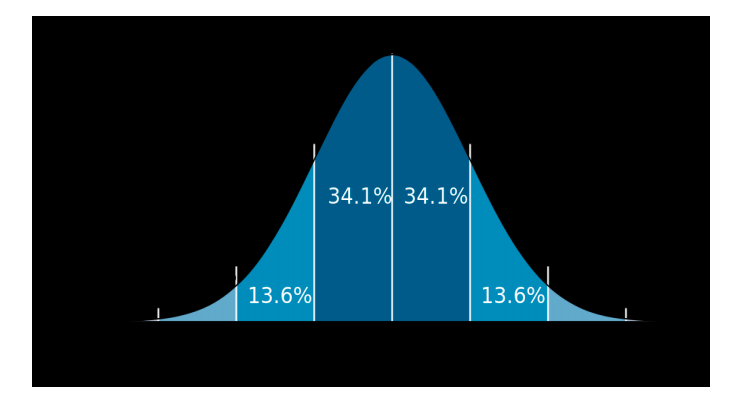
  • Gaussian Distribution


    Gaussian (Normal) Distribution


    maths equation for Gaussian (Normal) Distribution

    Standard normal distribution with zero mean and variance equal to one:

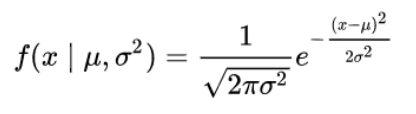
    maths equation for Standard normal distribution with zero mean and variance equal to one

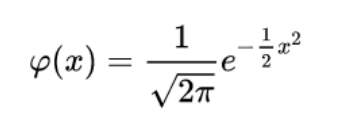
    Z-score


    Z-score represents the signed number of standard deviations by which the value of the data point is above the mean of the observed random variable.
    Z-score is positive if above the mean and negative if below it: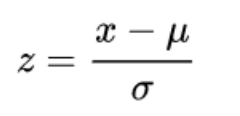

    zscore maths equation

    In Matlab, use qfunc to compute complementary cumulative distribution function

    complementary cumulative distribution graph

    Matlab


    Use randn to generate Gaussian random variable

    Use qfunc to find complementary cumulative distribution function

    Use zscore to find the z-score of random variables


    Example with zscore and Gaussian distribution


    Suppose X is a random variable that has normal distribution with mean = 4 and standard deviation (SD) = 2.
    Do the following:




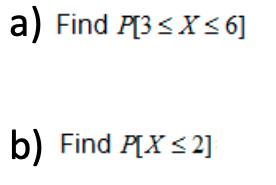
    Click here for solution

    Solution


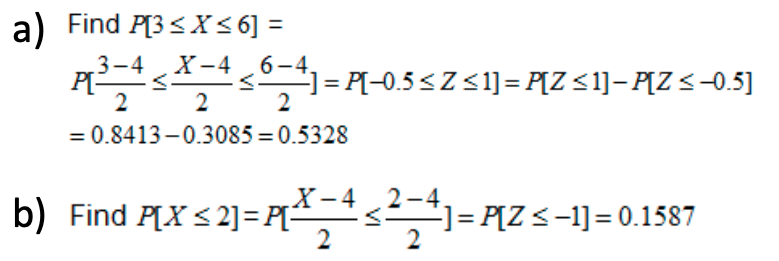
  • Insert Content Here 5
  • Insert Content Here 6
  • Insert Content Here 7