-
Introduction
This week you will learn about the specification, use, and implementation of the Queue ADT.
Objectives
1. Understanding and applying the Queue ADT.
2. Implementing a Queue using an array.
3. Queue applications.- Real world examples
- Cars in line at a petrol station
- People waiting in line for a film
- Computer world examples
- Jobs waiting to be executed
- Jobs waiting to be printed
- Round robin scheduler
- Any input buffer
- e.g Characters waiting to be processed
-
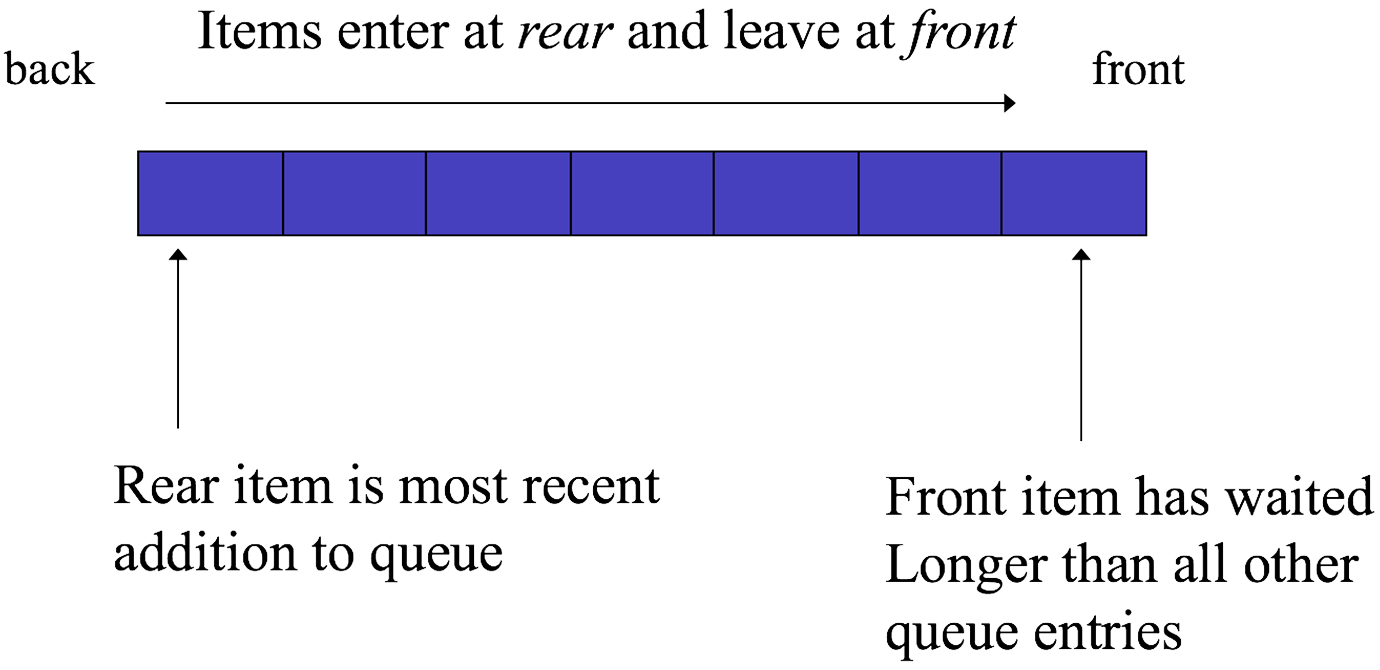
Common queue properties
- Queues have the property that, the earlier an item enters a queue, the earlier it will leave the queue. A queue has the following properties
- First in, first out (FIFO) data structure
- A queue is a restricted form of a list.
- Additions to the queue must occur at the rear (back).
- Deletions from the queue must occur at the front
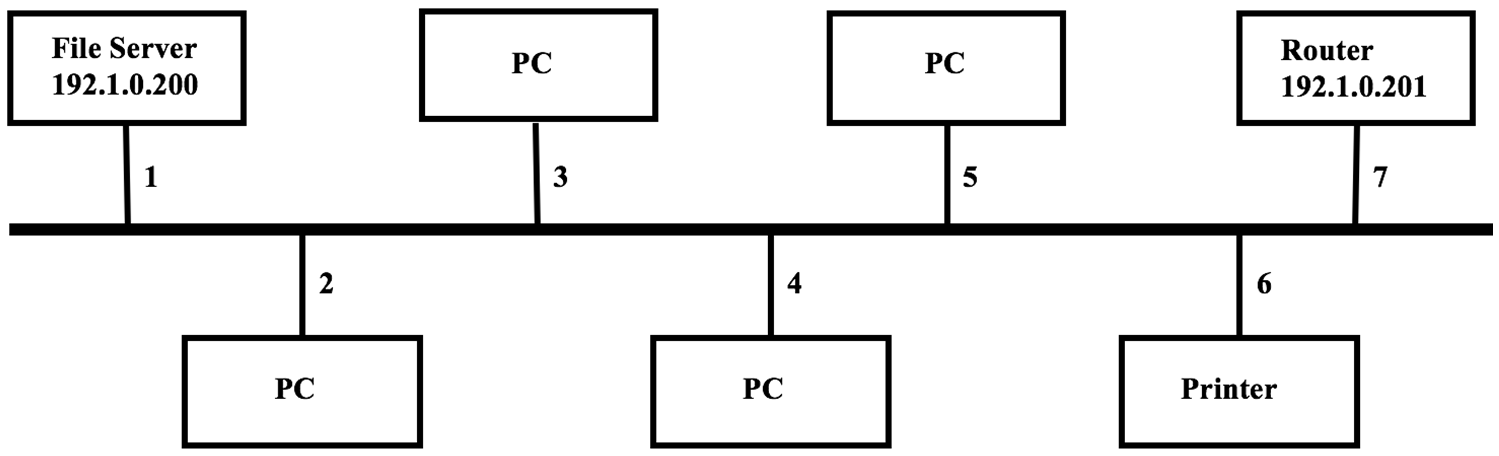
Example: Ethernet and printers
Ethernet is a set of protocols describing how devices on a network can communicate
Typical Ethernet configuration
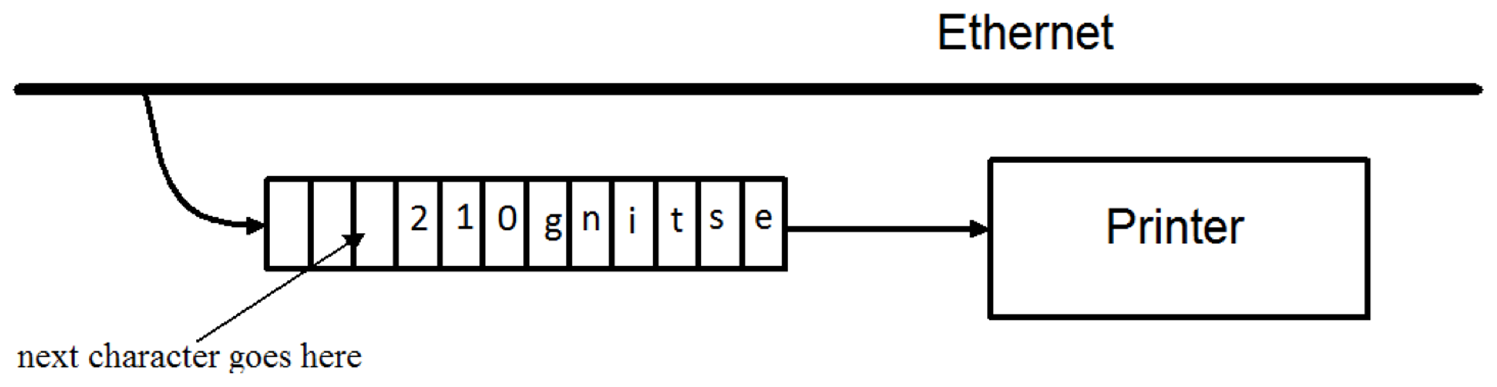
Devices place messages onto the network preceded by an ‘id number’ of the device the message is intended for. If two devices try to send messages at the same time a collision occurs and none of the messages are sent.
- Devices operate at differing speeds
- PC may place document on network at 100,000 cps
- Ethernet transmits document at >1,250,000 cps
- Printer may only processes 10,000 cps
How does the printer handle the pileup of characters sent by the PC?
Answer - Print buffers
A buffer is a queue. Incoming data is stored at the rear
It normally processes data in a FIFO manner, except when using a priority queue
eg print all small documents before large documents
-
Queue ADT
A Queue Q stores items of some type queueElementType, with First-In, First-Out (FIFO) access.
void Q.add( queueElementType e ) // sometimes called enqueue Precondition: None Postcondition: Qpost = Qpre with e added to the rear. queueElementType Q.remove( ) // sometimes called dequeue Precondition: !isEmpty() Postcondition: Qpost = Qpre with front removed Returns: The least-recently enqueued item (the front). queueElementType Q.peek( ) // sometimes called front Precondition: !isEmpty( ) Postcondition: Qpost = Qpre Returns: The least-recently enqueued item (the front) bool Q.isEmpty( ) Precondition: None Postcondition: None Returns: true if and only if Q is empty, i.e., contains no data items. bool Q.isFull( ) Precondition: None Postcondition: None Returns: true if and only if Q is full, i.e., cannot store any more data items. int Q.length( ) // sometimes called size Precondition: !isEmpty( ) Postcondition: Qpost = Qpre Returns: number of data items in Q.
-
Code Example: Queues vs. Stacks
// … read characters until '.' found, adding each char to Q and S. get input character; while input character not equal to '.‘ begin q.add( character ); s.push( character ); get input character; end while while ( ! q.isEmpty( ) ) begin output "Q: " + q.remove( ) + '\t'; output "S: " + s.pop( ) + '\n'; end while stopSample program output, given input sequence a b c:
Q: a S: c
Q: b S: b
Q: c S: aNB. Queues preserve order while stacks reverse it.
Worked Exercise:
What is the output resulting from the following sequence, where q is an initially empty queue of int:
q.addQ( 1 ); q.addQ( 2 ); q.addQ( 3 ); output q.front( ); output q.removeQ( ); output q.front( ); if ( q.isEmpty( ) ) output "empty\n"; else output "not empty\n"; end ifProgram analysis – 📷 array implementation
X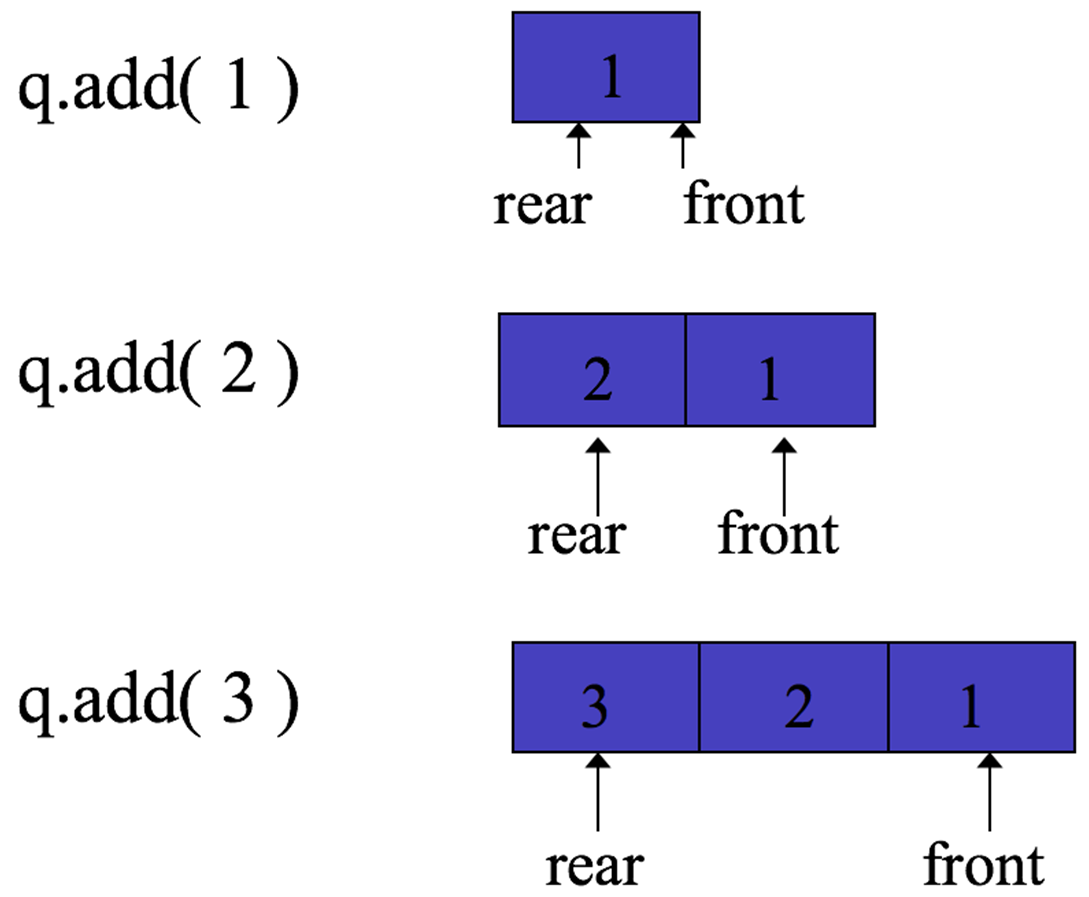 X
X
-
Array implementation
Must keep track of front and rear (more complicated than a stack)
With data in a queue, implemented as an array, rear will normally be greater than front.
There are 3 special situations which must be addressed
1. Rear < front (empty queue)
2. Rear = front (one-entry queue)
3. Rear = array size (full queue)Examples:
📷 Enqueueing
📷 Various queue states
📷 DequeueingX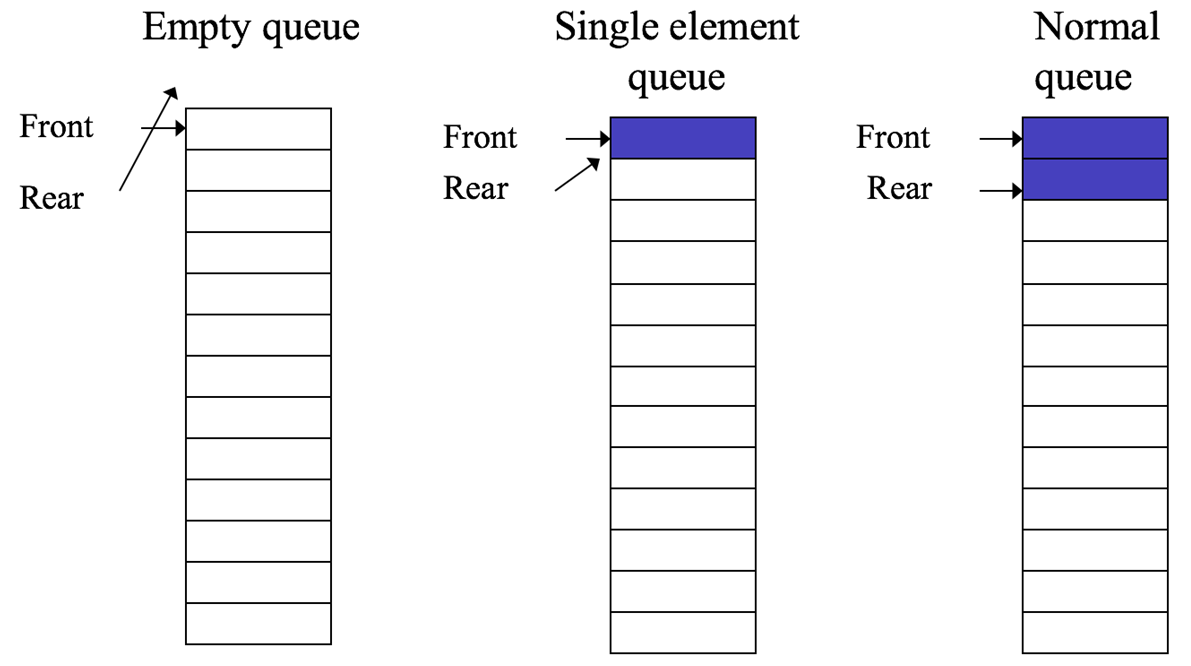 X
X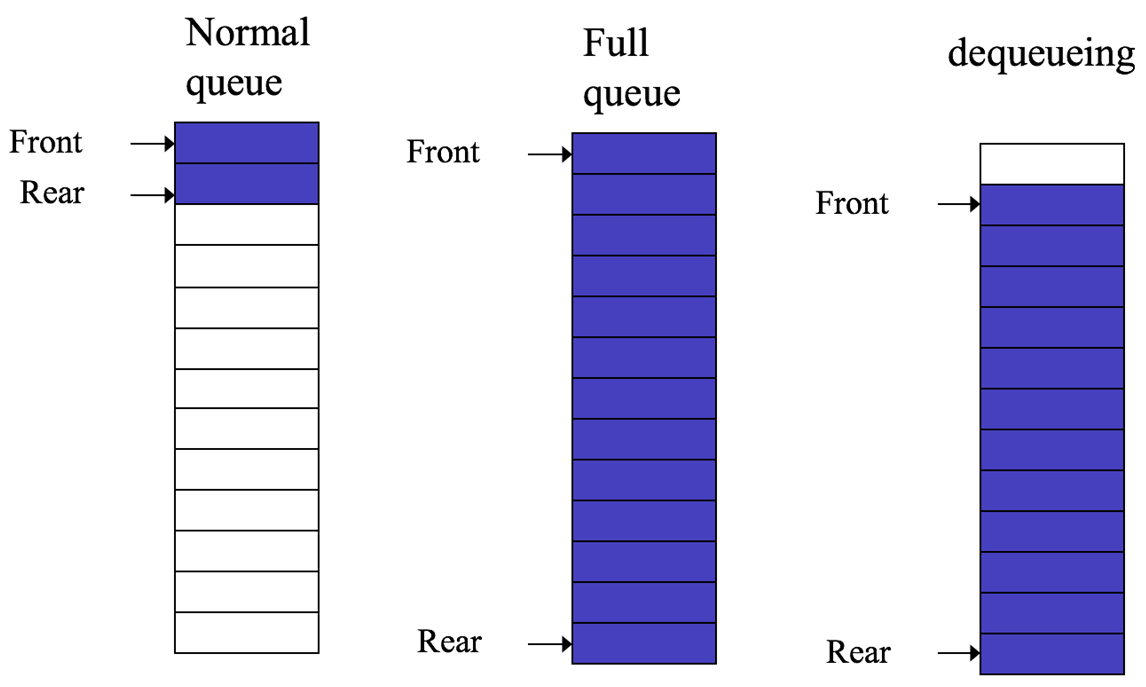 X
X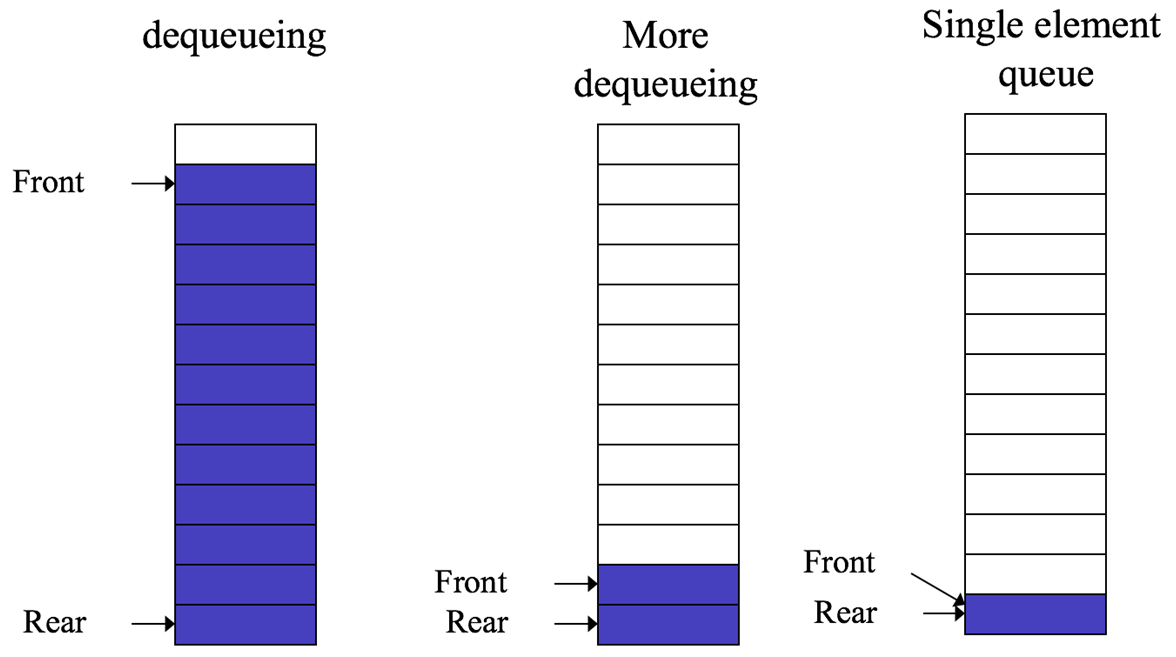
-
Queue creator (constructor)
// set up the queue front and back begin createQ( ) set queueFront to 0; set queueRear to -1; end createQ;
add( ) algorithm
// function to add an item onto the front of the queue begin add( queueElement qe ) if ( queueFull ) begin output "Queue is full\n"; set ok to false; end else begin inc queueRear; set queue[ queueRear ] = qe; set ok to true; end if return ok; end add;remove( ) algorithm
// function to remove the top item from the queue myQueue begin remove(queueElement qe) if ( queueEmpty ) output "Queue is empty\n"; set ok to false; end else begin qe = queue[ queueFront ]; inc queueFront; set ok to true; end if return ok; end remove;queueEmpty( ) and queueFull( )
// function checks to see if the queue is empty begin queueEmpty( ) return queueFront > queueRear; end queueEmpty; // function checks to see if the queue is full begin queueFull( ) // N.B. use -1 because array starts at zero for first array item return queueRear == ( maxQueueSize - 1 ); end queueFull;
-
ADTQueue in Java
This is a Java interface to define a Queue ADT. Note that for simplicity this defines a queue that stores string data. This could be changed to use generics and store any kind of data elements as shown in the linked list example you saw previously.
public interface ADTQueue { void createQueue(); int size(); boolean isEmpty(); boolean isFull(); String front(); boolean enqueue(String s); String dequeue(); }eg public class MyQueue implements ADTQueue
String Queue
This shows part of a possible implementation of our Queue ADT, showing the fields of the class and the createQueue operation.
public class SimpleQueue implements ADTQueue { private String[] q; private static final int MAXELEMENTS = 10; private int front; private int rear; private int length; public void createQueue() { q = new String[MAXELEMENTS]; front = 0; rear = -1; length = 0; } -
A problem

We cannot increase rear beyond the limits of the array. Therefore, this queue must be regarded as full, even though there are plenty of available memory cells. One way to solve this might be to Wait until the queue empties out and Then reset it and start again. In the computer processing job example however, this would be unacceptable since many jobs could arrive while the queue is emptying out.
Another difficulty
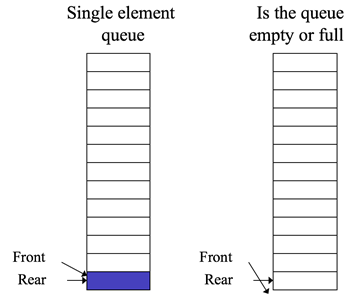
Our definition of empty is rear < front, so it is empty. But, rear has reached its limit. It cannot go beyond the array, Therefore, the queue is full!
The solution: 📷 wrapping around
Example:
Queue is an array of 4 elements. We wish to enqueue (Q.add) and dequeue (Q.remove) multiple items.
Enqueue and dequeue operations
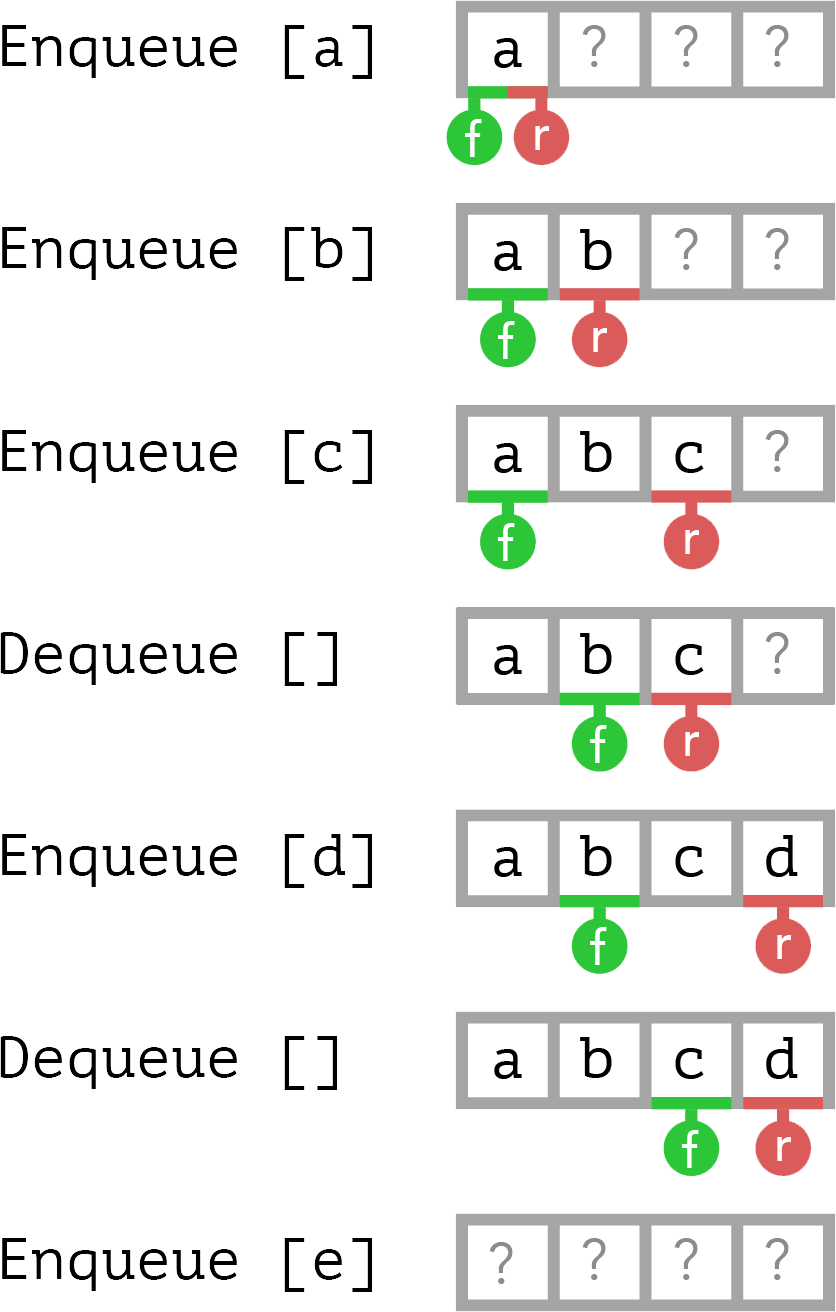 X
X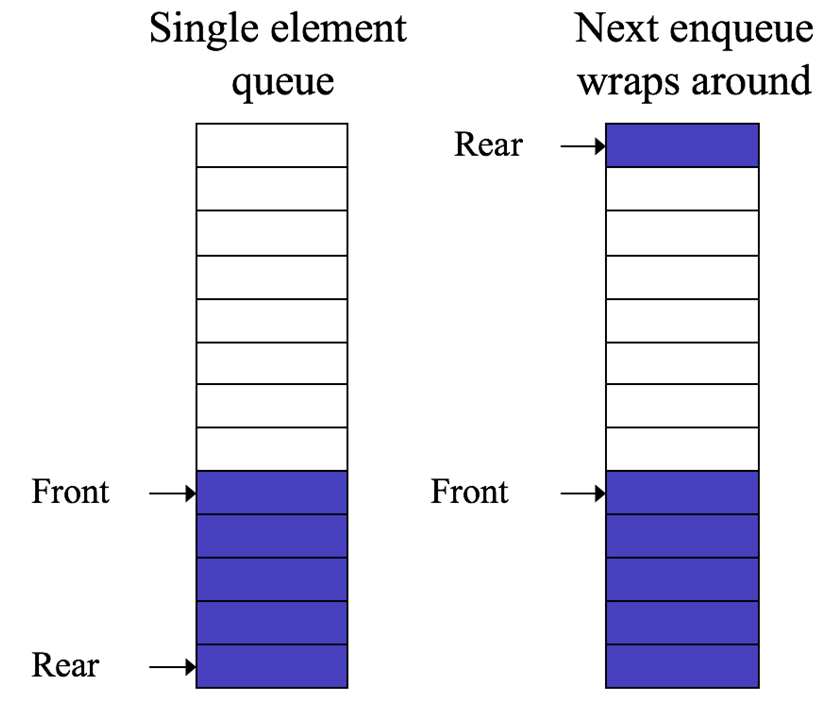 X
X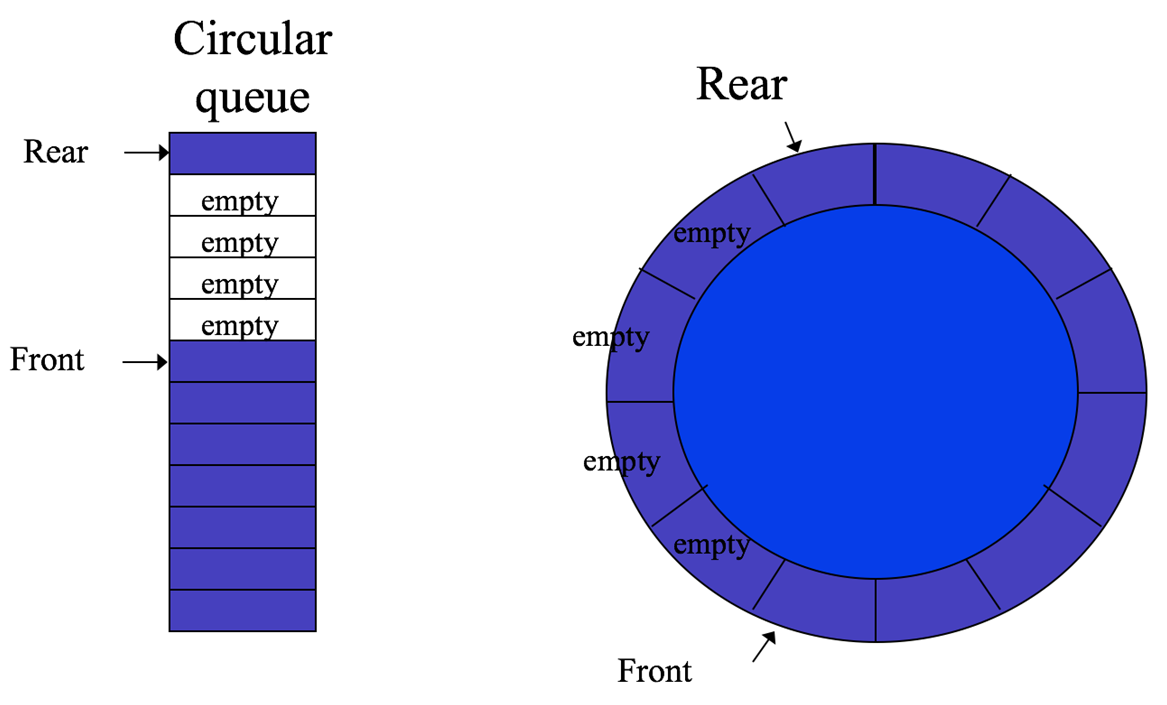
-
A paradox
With an array, it is easy to run out of space in the queue to enqueue (Q.add) items and yet still have unused memory cells that can store data! To get around this, we have to make it possible to ‘wrap around’. Both ‘rear’ and ‘front’ must be able to wrap around.
- How to wrap around:
- If rear + 1 > MAXQUEUESIZE -1 then set rear to 0
- OR preferable to use modulo operator
- rear = (rear+1) % MAXQUEUESIZE
- NB same goes for front
- front = (front) % MAXQUEUESIZE
Main issues (full and empty)
Wrapping around allows us to avoid an erroneous ‘full’, but, it means that we cannot use ‘rear < front’ as a test of whether the queue is empty because rear will become < front as soon as it wraps around
If there is one element in the queue then rear should be the same as front, therefore, rear must start < front.
You could check for an empty queue with something like: nextPos(rear) == front, but, when the queue is full it is also true that nextPos(rear) == front!
Solution
To solve this dilemma we let the definition of empty use the length() method
Then the test for empty is length() == 0, and the test for full is length == MAXQUEUESIZE
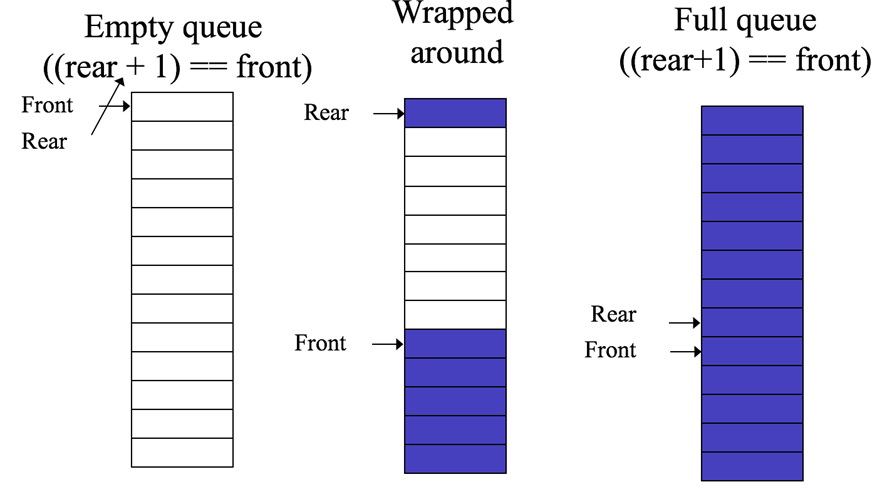
Explanation using conventional arrays Solution
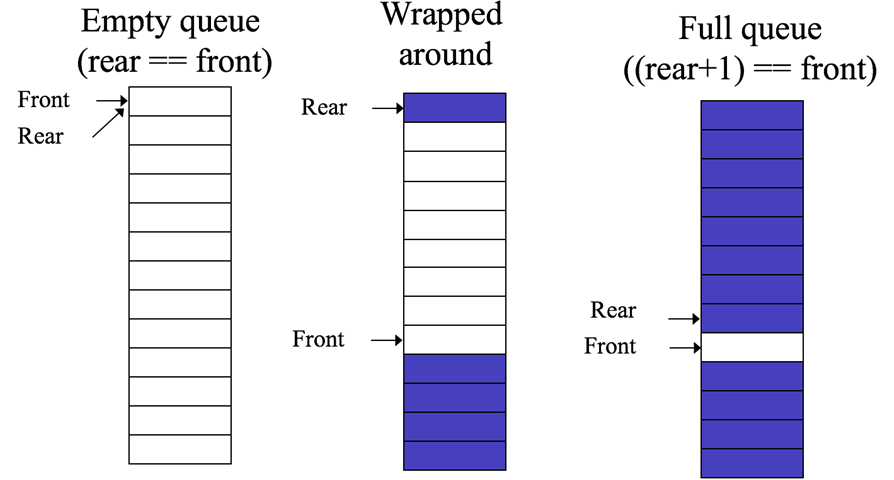
-
Implementation of Enqueue
The following example shows how the enqueue operation can be coded for our String queue:
public boolean enqueue(String s) { if (isFull() == false) // checks if space in queue { rear++; if (rear == MAXELEMENTS - 1) { rear = 0; } q[rear] = s; length++; return true; } else { return false; // to indicate failure } }The full implementation of the SimpleQueue class is left as a lab exercise.
Linked list implementation
Array-based queues, like array based stacks have the disadvantage that they are static structures.
- Dynamic queues, on the other hand:
- Do not have unused space
- Do have extra memory requirements (for references/pointers)
- Do not run out of space, unless there is no more room on the heap
How could you build a dynamic queue class to implement our Queue ADT? As for the dynamic stack class, this could be based on the linked list implementation you have seen. Since we want to add items at one end, and remove from the other end, this is done efficiently if a doubly linked list is used. Note that there is no need in the dynamic queue to wrap round, as in the array implementation.
-
A Queue Application - Message Queue
- Queues are often used for sending and receiving asynchronous messages. Asynchronous means that the sender does not wait for a response from the receiver, but assumes that the receiver will get the message at some later time. For example, when you use a mobile phone you can communicate either synchronously or asynchronously:
- Synchronous: Talk – callers communicate in real time conversation, content is “processed” immediately, not stored
- Asynchronous: Text/email – messages are sent and stored until read. In asynchronous communication the messages are usually stored in some intermediate location, e.g. a queue or mailbox.
Asynchronous messages can obviously be used for communication between people. They can also be used in some situations for communication between components of a software system.
Message queue example
The following Java code shows four classes, Message, MessageSender and MessageReceiver, that make up a very simple text message system. MessageSender and MessageReceiver both need to use an instance of SimpleQueue to send/get messages. MessageTester is a simple test programme that creates a queue, and makes a MessageSender send messages to be received by a MessageReceiver. The messages are received in the order that they were sent, and the receiver can get one message at a time, or get all the messages from the queue at once.
import java.util.*; import java.text.*; public class Message { public StringBuffer sender; public StringBuffer recipient; public StringBuffer content; public Date date; public Message() { String sender = "unknown sender"; this.sender = new StringBuffer(sender); String recipient = "unknown recipient"; this.recipient = new StringBuffer(recipient); String content = "none"; this.content = new StringBuffer(content); this.date = new Date(); } public Message(String sender, String recipient, String content) { this.sender = new StringBuffer(sender); this.recipient = new StringBuffer(recipient); this.content = new StringBuffer(content); this.date = new Date(); } public String getDate() { return DateFormat.getDateTimeInstance().format(this.date); } @Override public String toString(){ StringBuffer s = new StringBuffer(); s.append("From:"); s.append(sender); s.append(",To:"); s.append(recipient); s.append(",Content: "); s.append(content); s.append(",Date: "); s.append(getDate()); return s.toString(); } } public class MessageSender { public void sendMessage(Message m, SimpleQueue q) { if(!q.isFull()) q.enqueue(m.toString()); else System.out.println("Cannot send - queue is full"); } } public class MessageReceiver { public void receiveMessage(SimpleQueue q) { String s = q.dequeue(); if (s != null) { System.out.println(s); } else System.out.println("No messages to receive"); } } public class MessageTester { public static void main(String[] args) { SimpleQueue q = new SimpleQueue(); q.createQueue(); MessageSender ms = new MessageSender(); MessageReceiver mr = new MessageReceiver(); Message m1 = new Message("Bob", "Alice", "Hello"); Message m2 = new Message("Jane", "Joe", "Good morning"); Message m3 = new Message("Jack ", "Jill", "See you later"); Message m4 = new Message("George", "Mildred", "Good evening"); Message m5 = new Message("Diane", "Sam", "Bye for now"); ms.sendMessage(m1, q); ms.sendMessage(m2, q); ms.sendMessage(m3, q); mr.receiveMessage(q); ms.sendMessage(m4, q); ms.sendMessage(m5, q); while (!q.isEmpty()) { mr.receiveMessage(q); } } } -
Priority queues
Queues are often prioritised
- Example, university registration queue
- Priority 1: 1st years
- Priority 2: 2nd years
- Priority 3: 3rd years
- Priority 4: 4th years
- Operating systems often prioritize their print queues so that large output does not monopolize the printer during peak times e.g.
- Priority 1: 5 pages or less
- Priority 2: 6-30 pages
- Priority 3: >30 pages
📷 Processing a new job
📷 Enqueueing of a priority 2 job
📷 What does this indicate? Priority 2 is emptyX X
X X
X X
X
-
Summary
- The Queue ADT is a FIFO data structure characterised by the operations enqueue and dequeue.
- The Queue ADT can be implemented using either an array, which has a fixed maximum size, or a linked list which can grow dynamically.
- When implemented with an array, it is important to allow the front and rear of the queue to wrap round (a circular queue) to prevent the queue filling up rapidly as items are added and removed
- The Queue ADT can be used for asynchronous messaging
- Queues are often prioritised – priority queue