8. The Cartesian product of sets

In the sets we have seen up to now the elements are not listed in any particular order. An ordered $n$-tuple is a list of $n$ elements arranged in a specified order and enclosed in parenthesis rather than curly brackets. For example, the $n$-tuple

$(a_1, a_2, a_3, \cdots, a_n)$

has $a_1$ as its first element, $a_2$ as its second element, etc.

Two ordered $n$-tuples are equal if and only if their corresponding elements are equal.

We have actually come across $n$-tuples before in the unit on vectors where we saw ordered 2-tuples and 3-tuples representing position vectors of points in 2-D and 3-D space respectively.

If $A$ and $B$ are two sets the Cartesian product of $A$ and $B$ is the set

$A \times B = \{(a, b) : a \in A \;\text{and}\; b \in B\}$

which is read as “ $A$ cross $B$”.

Two elements in the set $A \times B$, say, $(a_1, b_1)$ and $(a_2, b_2)$ are equal if and only if they have the same first element, i.e. $a_1 = a_2$ and the same second element, i.e. $b_1 = b_2$.

When $A = B$ we write $A^2$ for $A \times A$.

The concept of a product of sets can be extended to any number of finite sets.

For the sets $A_1, A_2, A_3, ..., A_n$ the Cartesian product

$A_1 \times A_2 \times A_3 \times \cdots \times A_n$

is the set of all ordered $n$-tuples

$(a_1, a_2, a_3, \cdots , a_n)$

where $a_1 \in A_1, a_2 \in A_2, \cdots , a_n \in A_n$

Note that, in a similar manner to writing $A^2$ for $A \times A$ we write

$A^n = A \times A \times A \times \cdots \times A$

for the $n$-fold Cartesian product of the set $A$ with itself.

Example 25

(i). $A = \{a, b, c\}$ and $B = \{u, v\}$ then

$A \times B = \{(a, u), (a, v), (b, u), (b, v), (c, u), (c, v)\}$

$B \times A = \{(u, a), (u, b), (u, c), (v, a), (v, b), (v, c)\}$.

From this example we see that $A \times B$ and $B \times A$ are different sets.

(ii). If $R = \{1, 2\}, S = \{x, y\}$ and $T = \{\alpha ,\beta \}$ then two of the six possible Cartesian products are

$R \times S \times T = \{(1, x, \alpha), (1, x, \beta), (1, y,\alpha ), (1, y, \beta),$

$(2, x,\alpha ), (2, x, \beta), (2, y,\alpha ), (2, y, \beta)\}$

$T \times S \times R = \{(\alpha , x, 1), (\beta ,x, 1), (\alpha , y, 1), (\beta , y, 1),$

$(\alpha , x, 2), (\beta , x, 2), (\alpha , y, 2), (\beta , y, 2)\}$.

We can continue in this way and form all six possible products to show that they are different.

Exercise: Determine the remaining four products.

End of Example 25

8.1. Cardinality of a Cartesian product

If $A$ and $B$ are non-empty finite sets with cardinality $\mid A \mid$ and $\mid B \mid$ respectively then the cardinality of the Cartesian product, $A \times B$ is given by

$\mid A \times B \mid = \mid A \mid \times \mid B \, \mid$.

This result is easily extended to determine the cardinality of the Cartesian product of any number of finite sets. For example, if the set $A$ has cardinality $\mid A $ then the cardinality of the $n$-fold Cartesian product of set $A$ with itself is,

$\mid A^n \mid = \mid A \times A \times A \times \cdots \times A \mid$

$= \mid A \mid \times \mid A \mid \times \mid A \mid \times \cdots \times \mid A \mid$.

$= \mid A \mid ^n$.

Example 26

Determine the cardinality of the Cartesian product of the sets in Example 25.

Solution

(i). Here $A = \{a, b, c\}$ and $B = \{u, v\}$

Then $\mid A \mid = 3$ and $\mid B \mid = 2$ so that

$\mid A \times B \mid = \mid A \mid \times \mid B \mid$

$= 3 \times 2 = 6$.

This result is easily verified since the number of elements in $A \times B$, as calculated in Example 25(i), is 6.

Note that $B \times A$ also contains 6 elements.

(ii). Here $R = \{1, 2\}, S = \{x, y\}$ and $T = \{ \alpha,\beta \}$

Then $\mid R \mid = 2, \mid S \mid = 2$ and $\mid T \mid = 2$ so that

$\mid R \times S \times T \mid$ $= \mid R \mid \times \mid S \mid \times \mid T \mid$

$= 2 \times 2 \times 2 = 8$.

This result is easily verified since the number of elements in $R \times S \times T$, as calculated in Example 25(ii), is 8.

Note that all other triple Cartesian products in this example will have 8 elements.

End of Example 26

9. Computer representation of sets

Let $U$ be the universal set which is finite of size $n$. Sets can be represented on a computer by bit strings where the number of bits equals the number of elements in the universal set.

For example, a subset $A$ of $U$ where

$A = \{a_1, a_2, a_3, \cdots , a_n\}$

can be represented by a bit string where the $i$-th bit in this string is $1$ if $a_i$ is in $U$ and is $0$ if $a_i$ is not in $U$.

Example 27

Let the universal set be all positive integers less than 10, i.e.

$U = \{1, 2, 3, 4, 5, 6, 7, 8, 9\}$.

The elements are ordered in increasing order so that $a_i = i$ .

(i). Define a subset $X$ to contain all the even integers in $U$, i.e.

$X = \{2, 4, 6, 8\}$.

The bit string representation of $X$ will have length $n = 9$ and contain a $1$ at the position of each even integer in $U$ and a $0$ otherwise, i.e.

$010101010$.

(ii). Define a subset $Y$ to contain all the odd integers in $U$, i.e.

$Y = \{1, 3, 5, 7,9\}$.

The bit string representation of $Y$ is $101010101$.

(iii). Define a subset $P$ to contain all the prime numbers in $U$, i.e.

$P = \{2, 3, 5, 7\}$.

The bit string representation of $P$ is $011010100$.

Although we do not consider it here we could now apply the bitwise OR and bitwise AND operations respectively to form the union and intersection of these sets.

End of Example 27

Example 28

In computing the set of all ASCII characters is a standard set of 128 characters where each character has a unique numeric code from 0 to 127. The 8-bit binary equivalent, from $00000000$ to $011111111$, of the numeric code is used in many computers for the internal representation of character data.

Further reading on binary numbers can be found at 🔗 Binary 01: Introduction to binary numbers

End of Example 28

Example 29

The representation of car licence plates on a computer involves taking the Cartesian product of sets that include letters and digits as elements.

In a certain country car licence plates consist of six characters, the first three are letters while the last three are digits.

If the letter $L$ denotes the set of letters and the letter $D$ the set of digits, i.e.

$L = \{A, B, C, \dots, Z\}$ and $D = \{0, 1, 2, \dots, 9\}$

then a licence plate such as TSC431 will correspond to the element

$(T, S, C, 4, 3, 1)$

of the set

$L \times L \times L \times D \times D \times D$

of all valid licence plates formed by taking the Cartesian product of the sets $L$ and $D$.

The element $(T, S, C, 4, 3, 1)$ is then converted to the equivalent ASCII form

$(84, 83, 67, 52, 51, 49)$

whose 8-bit binary representation is

$(01010100\;\; 01010011 \;\; 01000011\;\; 00110100 \;\; 00110011 \;\; 00110001)$.

Note that number systems, including binary numbers, are to be studied in detail in a later chapter. In the meantime for converting from decimal format to binary, as in the example above, the reader is directed to the following links,

🔗 Converting from decimal to binary

🔗 Converting larger number from decimal to binary

End of Example 29

Example 30

A computer can represent colours in a digital image using 8-bit numbers. A total of 256 shades of colour can be represented by all the possible combinations of zeros and ones. In the RGB system the amount of the primary colours, red, green and blue required to mix together to produce another colour is represented by an integer in the range 0 to 255 (8 bits).

Hence, if the set

$S = \{0, 1, 2, \dots, 255\}$

then any given colour is a member of the set formed by the Cartesian product

$S \times S \times S$.

Some common representations are:

Colour		24-bit representation
Red	(255, 0, 0)	(11111111 00000000 00000000)
Green	(0, 255, 0)	(00000000 11111111 00000000)
Blue	(0, 0, 255)	(00000000 00000000 11111111)
Black	(0, 0, 0)	(00000000 00000000 00000000)
White	(255, 255, 255)	(11111111 11111111 11111111)

Read more about how a computer represents colours as numbers here

🔗 How Does a Computer Represent Colors as Numbers?

End of Example 30

10. Intervals

The real numbers (of which the integers are a subset) can be represented as points on a horizontal line that extends from a point called the origin in both directions towards minus infinity ($- \infty$) to the left and plus infinity ($+ \infty$) to the right. The real number line, shown in the diagram below, is denoted by $\mathbb{R}$.

When comparing numbers the order in which they are placed on the number line will determine whether they are greater than, or less than, each other.

In mathematics it often happens that we are only interested in certain subsets of the real numbers, and we call these subsets intervals. Roughly speaking an interval can be defined as a set of numbers that starts at one number and ends at another. We must however specify whether or not the endpoints are contained in the interval.

Example 31

(i). An interval can be represented by a pair of numbers enclosed in either square brackets or parentheses respectively depending on whether the end points of the interval are included or excluded.

For example, $[-5, 6)$ corresponds to the interval on the real number line that includes the endpoint $-5$, hence the square bracket, but excludes the endpoint $6$, hence the parenthesis.

(ii). In set notation we let the universal set be the set $\mathbb{R}$ of all real numbers and define a set $S$, corresponding to the interval in part(i) as follows:

$S = \{x \in \mathbb{R} : - 5 \le x < 6 \}$.

We read this as “the set of all real numbers $x$, such that $x$ is greater than or equal to $-5$ and strictly less than $6$”.

(iii). Pictorially the interval $[-5, 6)$ is shown as

The ‘filled circle’ indicates the left-hand endpoint at $-5$ is included while the ‘empty circle’ at $6$ shows the right-hand endpoint at $6$ is excluded.

Parentheses therefore correspond to the $<$ and $>$ symbols and empty circles, while square brackets correspond to the symbols $\le$ and $\ge$ and filled circles.

End of Example 31

10.1 Interval notation

The main types of interval are defined below using interval notation, set notation and pictorially as regions of the real number line.

Let $a, b \in \mathbb{R}$ where $a < b$.

(i). The open interval from $a$ to $b$ contains neither of its endpoints.

in interval notation write $(a, b)$

in set notation write: $\{x \in \mathbb{R}: a < x < b\}$

pictorially the open interval $(a, b)$ is shown as

(ii). The closed interval from $a$ to $b$ contains both its endpoints.

in interval notation write $[a, b]$

in set notation write: $\{x \in \mathbb{R} ; a \le x \le b\}$

pictorially the closed interval $[a, b]$ is shown as

The above notation can be extended to define the half-open intervals $(a b]$ and $[a b)$, also called half-closed intervals, that include one endpoint:

(iii). The interval from $a$ to $b$ with left open and right closed.

in interval notation write $(a\; b]$

in set notation write: ${x \in \mathbb{R} : a < x \le b}$

pictorially the half-open interval $(a\; b]$ is shown as

(iv). The interval from $a$ to $b$ with left closed and right open.

in interval notation write $[a \; b)$

in set notation write: $\{x \in \mathbb{R}: a \le x < b\}$

pictorially the half-open interval $[a \; b)$ is shown as

Some intervals may have no lower or upper bound and so we use the $- \infty$ and $+ \infty$ symbols respectively for these situations. Note that $- \infty$ and $+ \infty$ are not numbers.

An “endpoint” of $- \infty$ or $+ \infty$ always corresponds to parentheses.

(v). The interval starting at, but not including, $a$ with no upper bound.

in interval notation write $(a, \infty)$

in set notation write: $\{x \in \mathbb{R} : x > a\}$

pictorially the interval $(a, \; \infty)$ is shown as

(vi). The interval starting at, and including, $a$ with no upper bound.

in interval notation write $[a, \infty)$

in set notation write: $\{x \in \mathbb{R}: x \ge a \}$

pictorially the interval $[a, \infty)$ is shown as

(vii). The interval with no lower bound up to, but not including, $b$.

in interval notation write $(- \infty, \; b)$

in set notation write: $\{x \in \mathbb{R} : x < b \}$

pictorially the interval $(- \infty, \; b)$ is shown as

(viii). The interval with no lower bound up to, and including, $b$.

in interval notation write $(- \infty, \; b]$

in set notation write: $\{x \in \mathbb{R} : x \le b \}$

pictorially the interval $(- \infty, \; b]$ is shown as

(ix). The interval with no lower or upper bound, i.e. the set $\mathbb{R}$, of all real numbers

in interval notation write $(- \infty, \infty)$

in set notation write: $\{x \in \mathbb{R} : - \infty < x < \infty \}$

pictorially the interval $(- \infty, \infty)$ is shown as

10.2 Union and intersection

Given intervals on the real number line we can calculate the union and intersection of these intervals and express the result in set and interval notation.

Example 32

Let the universal set be the set $\mathbb{R}$ of all real numbers and define the sets $A$ and $B$ as follows:

$A = \{x \in \mathbb{R} : -5 \le x \le 6\}$.

$B = \{x \in \mathbb{R} : -6 < x < 5 \}$.

Determine each of the following expressing the answers in both set and interval notation

(i) $A \cup B$ (ii) $A \cap B$.

Solution

sketch a number line (graph) for each set.

include appropriate circles (filled or empty) to indicate whether or not the endpoints are included or excluded.

to identify the union take all the points included on either graph.

to identify the intersection take all the points included on both graphs.

The blue interval corresponds to the set $A$, i.e. the closed interval $-5 \le x \le 6$, and includes its endpoints, $-5$ and $6$.

The red interval corresponds to the set $B$, i.e. the open interval $-6 < x < 5$ , and does not include its endpoints, $-6$ and $5$.

(i). The interval that represents the union of $A$ and $B$ contains all the points that are in either $A$ or $B$ (or both).

Hence, $A \cup B$ is represented by the full range of values in the diagram giving,

Set notation: $A \cup B = \{x \in \mathbb{R} : -6 < x \le 6 \}$.

Interval notation: $A \cup B = (-6, \; 6]$.

(ii). The interval that represents the intersection of $A$ and $B$ contains the points that are common to both $A$ and $B$.

Hence, $A \cap B$ is represented by the overlap in the diagram giving,

Set notation: $A \cap B = \{x \in \mathbb{R} : -5 \le x < 5\}$.

Interval notation: $A \cap B = [-5, \; 5)$.

End of Example 32

Example 33

Let the universal set be the set $\mathbb{R}$ of all real numbers and define the sets $A$ and $B$ as follows:

$A = \{x \in \mathbb{R}: -4 < x < 7 \}$.

$B = \{x \in \mathbb{R} : -7 \le x < 5 \}$.

Determine each of the following expressing the answers in both set and interval notation

(i) $A \cup B$ (ii) $A \cap B$.

Solution

First we sketch a diagram. The set $A$ is shown in red and the set $B$ in blue.

(i). The interval $A \cup B$ is represented by the full range of values in the diagram.

Set notation: $A \cup B = \{x \in \mathbb{R} : -7 \le x < 7 \}$.

Interval notation: $A \cup B = [-7, \; 7)$.

(ii). The interval $A \cap B$ is represented by the overlap in the diagram.

Set notation: $A \cap B = \{x \in \mathbb{R} : -4 < x < 5 \}$.

Interval notation: $A \cap B = (-4, \; 5)$.

End of Example 33

10.3. Complement

An interval on the real number line is the set of all points that lie between two values which themselves may or may not be included in the interval. The complement is the set of all points on the real number line that do not lie in the given interval.

Example 34

Let the universal set be the set $\mathbb{R}$ of all real numbers and define the sets $A$ and $B$ as follows:

$A = \{x \in \mathbb{R} : -3 \le x \le 8 \}$.

$B = \{x \in \mathbb{R} : -7 \le x < 5 \}$.

Determine each of the following expressing the answers in both set and interval notation

(i) $A^c$ (ii) $B^c$(iii) $(A \cap B)^c$.

Solution

(i). The set $A$, as shown, contains the points between $-3$ and $8$ including the end values.

The complement, $A^c$, contains all the points that are not in $A$.

Set notation: $A^c = \{x \in \mathbb{R} : x < -3\; \text{or}\; x > 8 \}$.

Interval notation: $A^c = (- \infty,\; -3) \cup (8, \; \infty)$.

(ii). The set $B$ contains the points between $-7$ and $5$, including $-7$ but excluding $5$.

The complement, $B^c$, contains all the points that are not in $B$.

Set notation: $B^c = \{x \in \mathbb{R} : x < -7\; \text{or}\; x \ge 5 \}$.

Interval notation: $B^c = (- \infty, \; -7) \cup [5, \; \infty)$.

(iii). Sketch both sets $A$ and $B$.

The interval $A \cap B$ is represented by the overlap in the diagram as shown below,

Set notation: $A \cap B = \{x \in \mathbb{R} : -3 \le x < 5 \}$.

Interval notation: $A \cap B = [-3, \; 5)$.

Hence, $(A \cap B)^c$ includes all the points that are not in $A \cap B$.

Set notation: $(A \cap B)^c = \{x \in \mathbb{R} : x < -3 \;\text{or}\; x \ge 5 \}$.

Interval notation: $(A \cap B)^c = (- \infty, \; -3) \cup [5, \; \infty)$.

End of Example 34

10.4. Difference

Recall that the difference of two sets $A$ and $B$, written $A - B$, is the set that of all elements that belong to $A$ but not $B$.

Example 35

Let the universal set be the set $\mathbb{R}$ of all real numbers and define the sets $A$ and $B$ as follows:

$A = \{x \in \mathbb{R} : x < -3 \}$

$B = \{x \in \mathbb{R} : -4 \le x \le 6 \}$.

Determine each of the following expressing the answers in both set and interval notation

(i) $A - B$ (ii) $B - A$.

Solution

The set $A$ is shown in red below while the set $B$ is shown in blue.

(i). $A - B$ is the set that of all elements that belong to $A$ but not $B$ and we have

Set notation: $A - B = \{x \in \mathbb{R} : x < -4 \}$.

Interval notation: $A - B = (- \infty, \; -4)$.

(ii). $B - A$ is the set that of all elements that belong to $B$ but not $A$ we have

Set notation: $B - A = \{x \in \mathbb{R} : -3 \le x \le 6 \}$.

Interval notation: $B - A = [-3, \;6]$.

End of Example 35

10.5. Symmetric Difference

In Section 4.5 we saw that the symmetric difference of two sets $A$ and $B$, written $A \oplus B$, is the set of all elements that are in $A$ or $B$ but not in both. Using set notation we can write,

$A \oplus B = (A \cup B) - (A \cap B)$ or, alternatively,

$A \oplus B = (A - B) - (B - A)$

Example 36

Let the universal set be the set $\mathbb{R}$ of all real numbers and define the sets $A$ and $B$ as follows:

$A = \{x \in \mathbb{R} : -4 < x < 7 \}$

$B = \{x \in \mathbb{R} : -7 \le x < 5 \}$.

Determine $A \oplus B$, the symmetric difference of $A$ and $B$, expressing the answer in both set and interval notation.

Solution

Using the definition, $A \oplus B = (A \cup B) - (A \cap B)$ from Example 33 we have :

$A \cup B = \{x \in \mathbb{R}: -7 \le x < 7\} $, shown in red below

$A \cap B = \{x \in \mathbb{R}: -4 < x < 5 \}$ shown in blue.

Hence, $A \oplus B = (A \cup B) - (A \cap B)$

$= \{x \in \mathbb{R} : -7 \le x \le -4$ or $5 \le x < 7 \}$ (Interval notation)

$A \oplus B = [-7, \; -4] \cup [5, \; 7)$ (Set notation)

Sketching $A \oplus B$ we have :

$Sketching A \oplus B Interval Diagram$

Alternatively, use the definition, $A \oplus B = (A - B) \cup (B - A)$.

From Example 33, the following diagram shows the set $A$ in red and the set $B$ in blue.

Then $A - B = \{ x \in \mathbb{R}: 5 \le x < 7\}$ and $B - A = \{ x \in \mathbb{R} : -7 \le x \le 4 \}$.

Hence, $A \oplus B = (A - B) \cup (B - A)$

$= \{x \in \mathbb{R} : -7 \le x \le -4$ or $5 \le x < 7 \}$ (Interval notation)

$A \oplus B = [-7, \; -4] \cup [5, \; 7)$ (Set notation)

This is the same result as obtained above.

End of Example 36

Further Examples

To close this section we first take a brief look at a few more examples involving intervals, including combinations of more than two intervals. We then show how sets can be used to represent solutions to linear and quadratic inequalities.

Example 37

(i). Write the set represented by the diagram below

in both interval and set notation.

Solution

In this case there are three sections to consider.

Set notation: $\{x \in \mathbb{R} : x < 0, \; 0 < x < 2, \; x > 2 \}$.

or $\{x \in \mathbb{R} : - \infty < x < \infty, \; x \neq 0, \; x \neq 2 \}$.

Interval notation: $(- \infty, \; 0) \cup (0, \; 2) \cup (2,\; \infty)$.

(ii). Sketch the set

$\{x \in \mathbb{R} : x > 1$ and $x \neq 6\}$

and write its representation in interval notation.

Solution

Interval notation: $(1, \; 6) \cup (6, \; \infty)$.

End of Example 37

Example 38

Let the universal set be the set $\mathbb{R}$ of all real numbers and define the sets $A$, $B$ and $C$ as follows:

$A = \{x \in \mathbb{R} : -4 \le x \le 2 \}$

$B = \{x \in \mathbb{R} : 0 \le x < 6 \}$

$C = \{x \in \mathbb{R} : 1 < x \le 5 \}$.

Determine $(A \cap B) - C$ expressing the answer in both set and interval notation.

Solution

The set $A$ is shown in red, the set $B$ in blue and the set $C$ in green.

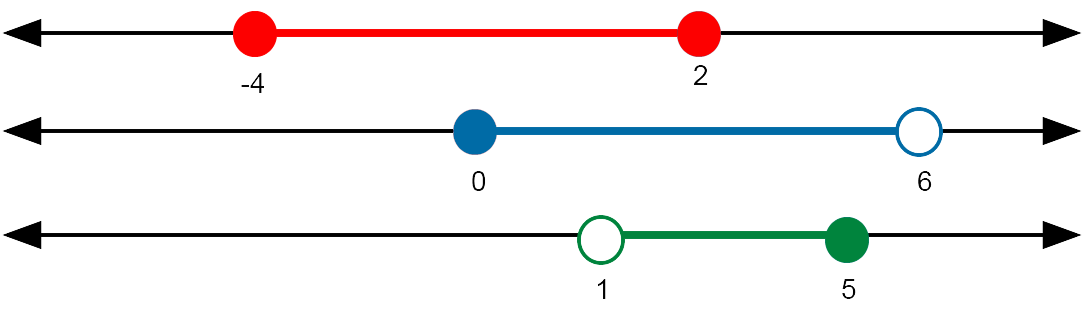
set A is shown in red, the set B in blue and the set C in green Interval diagrams

First we sketch the set $A \cap B$:

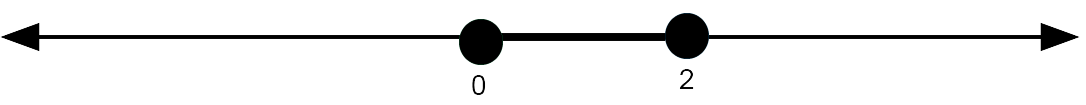
The set $(A \cap B) - C$ contains the elements that are in $A \cap B$ but not in $C$:

Set notation: $(A \cap B) - C = \{x \in \mathbb{R} : 0 \le x \le 1\}$.

Interval notation: $(A \cap B) - C = [0, \; 1]$.

End of Example 38

Example 39

(i). Solve the inequality $3(x + 1) < 4(3x - 2)$.

Sketch the set of solutions on the real number line and write the solution in both interval and set notation.

Solution

$3(x + 1) < 4(3x - 2)$

$3x + 3 < 12x - 8$

$11 < 9x$

${\Large\frac{11}{9}} < x$

$x > {\Large\frac{11}{9}}$

Interval diagram for the fracion x = eleven over nine

Set notation: $\{x \in \mathbb{R} : x > 11/9 \}$.

Interval notation: $(11/9, \; \infty)$.

(ii). Solve the inequality $x^2 + 3x < 10$.

Sketch the set of solutions on the real number line and write the solution in both interval and set notation.

Solution

We first solve the equation

$x^2 + 3x = 10$

$x^2 + 3x - 10 = 0$

$(x + 5)(x - 2) = 0$

$x = -5, \; x = 2$

Plotting these values in the diagram below splits the number line into three intervals:

$(- \infty, \; -5), \; (-5, \; 2)$ and $(2, \; \infty)$.

Define $p(x) = x^2 + 3x - 10$ and determine the interval(s) on which $p(x) < 0$ , i.e. where $p(x)$ is negative.

Choose a point in each interval and determine the sign of $p(x)$ at that point. The resulting value will be the sign of $p(x)$ over the entire interval containing the point.

Create a table as shown below:

$x$	-6	0	3
$p(x)$	8	-10	8
Sign	+	-	+
Interval	$(- \infty, \; -5)$	$(-5, \; 2)$	$(2,\; \infty)$

From the table the solution is:

Set notation: $\{x \in \mathbb{R} : -5 < x < 2 \}$.

Interval notation: $(-5, \; 2)$

End of Example 39

Summary

In this unit we have introduced the concept of a set and you should now be able to:

understand what is meant by a set and the elements of a set.

represent sets using both roster and predicate form.

define subsets, proper subsets and equivalent sets.

understand the concepts of union, intersection and complement of sets.

use Venn diagrams to provide pictorial representations of sets.

understand the concept of disjoint sets and a partition of a set.

calculate the cardinality of sets and unions of sets.

Determine the Cartesian product of two, or more, sets.

appreciate the application of sets in computing.

express subsets of the real number line in set and interval notation.

determine the union, intersection, complement, difference and symmetric difference of intervals on the real number line and present the results graphically.

use sets to represent solutions to linear and quadratic inequalities.

You should now attempt the tutorial exercises and Maple questions on GCU Learn.

The next unit introduces functions and their properties.

8. The Cartesian product of sets

8.1. Cardinality of a Cartesian product

9. Computer representation of sets

10. Intervals

Further Examples

Summary