-
1. Introduction
In this unit we look at the concept of a function and introduce some important functions that are fundamental in the study of mathematics and computing. The basic idea of a function is illustrated with a simple example before presenting some more formal definitions and terminology.
A function defines a relationship between the elements of two sets and we present different ways to express this relationship including arrow diagrams, formulae, graphs and lists of ordered pairs. We look at how to identify whether a relationship is a function before considering whether functions meet specific criteria that classify them as one-to-one and/or onto functions. The idea of an inverse function is then presented and we illustrate how to calculate an inverse function when it exists and interpret the results graphically. The process of combining two, or more, functions through composition is then discussed. The unit closes with a brief look at some functions that commonly occur in computing and mathematics.
1.1 Functions - some basics
In everyday problems the value of one variable depends for its value on another variable.
For example, suppose a shop is having a sale, reducing the price of every item in stock by 10 per cent. The sale price $P$ of an item will depend on its original price $x$, say, and the percentage reduction so that in this case $P$ will be ${\Large\frac{9}{10}}$ of $x$.
Hence, the original price and the sale price are connected by the relationship, $P = 0.9 x$.
Example 1
Determine the sale price if the original cost of an item is:
(i). £10 (ii). £20 (iii). £30.
Solution
(i). Replace $x$ with $10$ to give $P = 0.9 \times 10 = £9$.
(ii). Replace $x$ with $20$ to give $P = 0.9 \times 20 = £18$.
(iii). Replace $x$ with $30$ to give $P = 0.9 \times 30 = £27$ .
We can therefore determine the sale price $P$ of any item given its original price, $x$. Note that we must have $x > 0$ as no items have a zero or negative original price. For each value of $x$, called the independent variable, there is an unique value of $P$. Since the value of $P$ depends on $x$, it is called the dependent variable.
We say that $P$ is a function of $x$ and write this as $P = f(x)$.
The variable $x$ is the input to the function and $f(x)$, which is read as “$f$ of $x$”, is the output.
A flow diagram as shown below, sometimes called a function machine, can be used to illustrate the idea of a function:

A function is therefore a rule which operates on an input and produces a single output.
End of Example 1 -
2. Domain, codomain and range
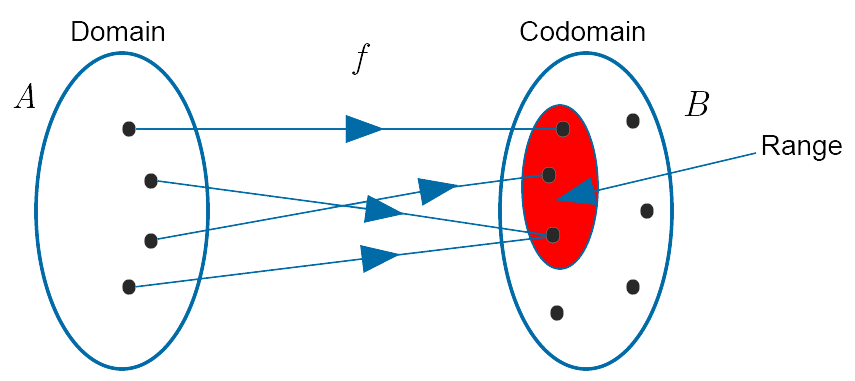
More formally, if we have a set $A$ and a set $B$ a function is a rule that assigns to each element of $A$ one and only one element of $B$.
We denote a function from $A$ to $B$ as $f : A \to B$ and say that “$f$ maps $A$ to $B$”.
The set $A$ on which $f$ is defined is called the domain of $f$ and the set $B$, in which $f$ takes it values, is called the codomain.
If $a \in A$ then $f(a)$ is the unique element of $B$ which the function $f$ assigns to $a$.
We say that “ $f(a)$ is the image of $a$ under $f$ ”, or equivalently, “ $f(a)$ is the value of $f$ at $a$”.
The set of all image values is called the range of $f$ , denoted $f[A] = \{f(a) : a \in A \}$.
Note that by definition the range is a subset of the codomain as shown in the diagram below.
- To summarise:
- The set of valid input values to a function is called the domain of the function.
- The set of all permissible output values is called the codomain of the function.
- The set of values which actually come out of the function is called the range of the function. The range is a subset of the codomain.
-
3. Identifying functions
It is important to be able to identify when a relationship between two sets represents a function. Equally, if the relationship is not a function we need to be clear as to why this is the case.
For a relationship to be a function each element in the domain is mapped to exactly one element in the range. The procedure is illustrated with some examples.
Further resources can be found at:
Testing if a relationship is a function - (watch all videos)
3.1. Functions as arrow diagrams
A relationship between finite sets can be represented diagrammatically by a collection of arrows pointing from the domain to the range.
Example 2
(i). The diagram shows a relation, $f_1$, between the sets $A = \{a, b, c, d\}$ and $B = \{1, 2, 3, 4\}$.
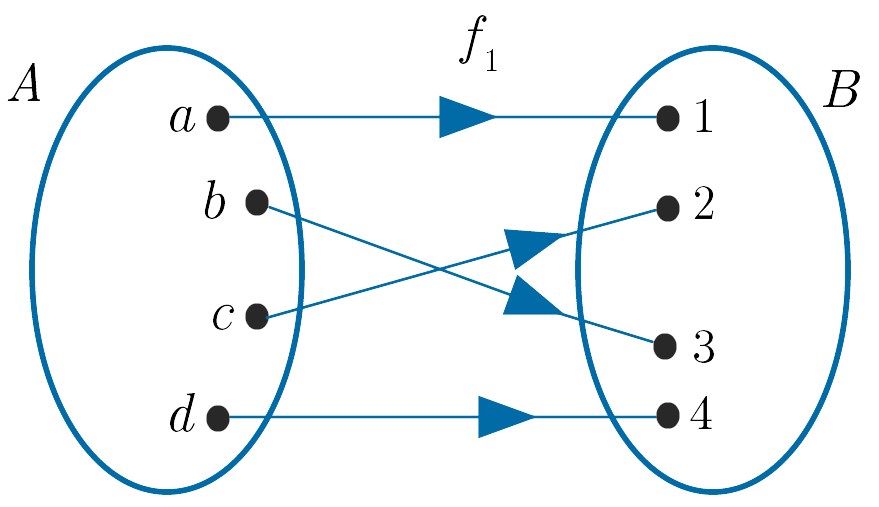
$f_1 : A \to B$ is a function as each element in $A$ has exactly one image in $B$.
We have that
$f_1(a) = 1$, $f_1(b) = 3$, $f_1(c) = 2$ and $f_1(d) = 4$.
The domain is the set, $A = \{a, b, c, d\}$.
The codomain is the set, $B = \{1, 2, 3, 4\}$.
The range is the set, $f_1[A] = \{1, 2, 3, 4\}$.
Note that the range is a subset of the codomain, i.e. $f_1[A] \subseteq B$.
In this case the range and the codomain are equal.
(ii). $f_2 : A \to B$ is a function as each element in $A$ has exactly one image in $B$.
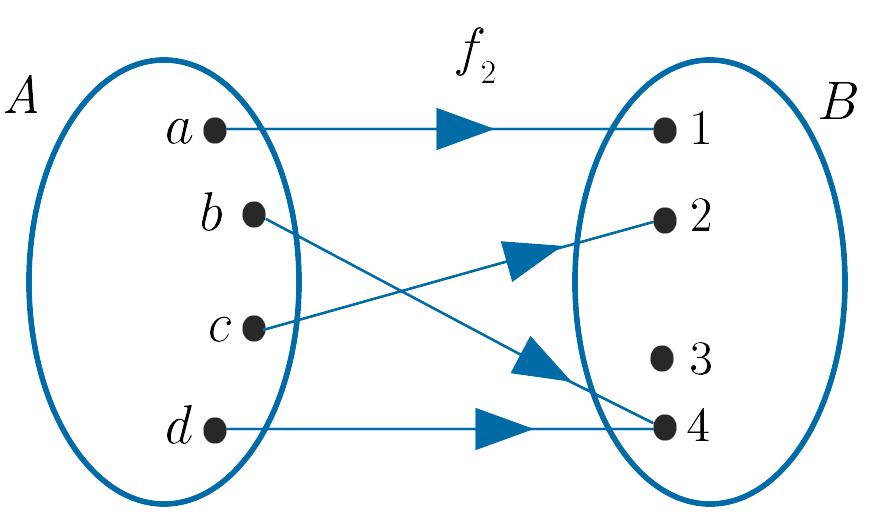
We have that
$f_2(a) = 1, f_2(b) = 4, f_2(c) = 2$ and $f_2(d) = 4$.
The domain is the set, $A = \{a, b, c, d\}$.
The codomain is the set, $B = \{1, 2, 3, 4\}$.
The range is the set, $f_2[A] = \{1, 2, 4\}.$.
Note that the range is a subset of the codomain, i.e. $f_2[A] \subseteq B$ Compare with the function in part (i)..
(iii). $f_3 : A \to B$ is not a function as the element $a$ in $A$ has more than one image in $B$, i.e.
$f_3(a) = 1$ and $f_3(a) = 4$.
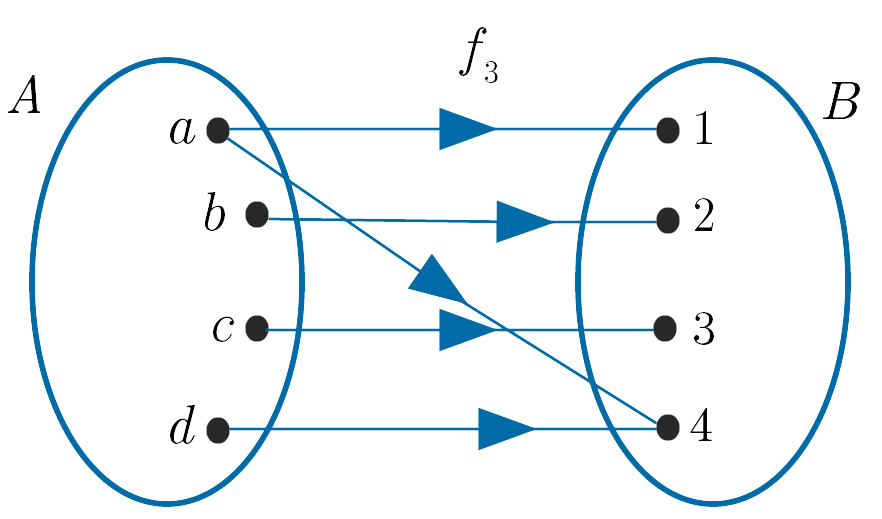
(iv). $f_4 : A \to B$ is a function as each element in $A$ has exactly one image in $B$.
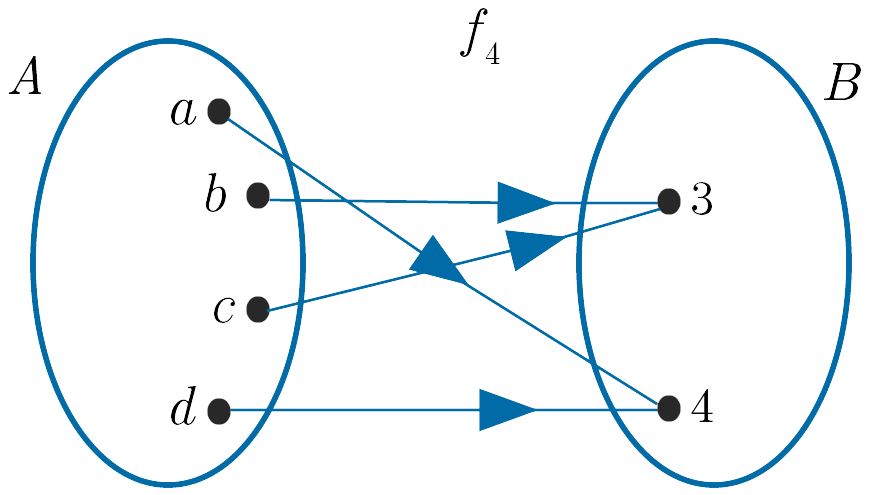
(v). $f_5 : A \to B$ is not a function as the element $c$ in $A$ does not have an image in $B$.
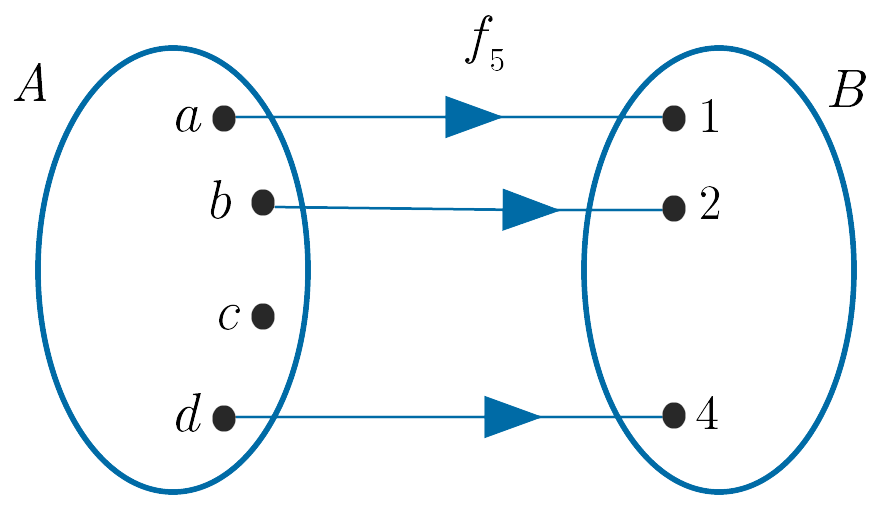 End of Example 2
End of Example 23.2. Functions as ordered pairs
In the next unit we introduce the concept of a binary relation between two sets $A$ and $B$. Essentially a relation is a set of ordered pairs that is a subset of $A \times B$, the Cartesian product of the sets $A$ and $B$. It turns out that functions are a type of relation and that a function $f$ can be represented as a set of ordered pairs, $(a, b)$ where the first component, $a$, is an element in the domain of $f$ and the second component, $b$, is an element in the range of $f$.
By definition for each input to a function there is exactly one output. So, given a list of ordered pairs if a first component is repeated then we do not have a function.
Example 3
Write each of the relations in Example 2 as a set of ordered pairs and determine whether or not they represent functions.
Solution
Referring back to Example 2 and treating each part of the question in turn.
(i). $\{(a, 1), (b, 3), (c, 2), (d, 4)\}$
This is a function as no two pairs have the same first component.
(ii). $\{(a, 1), (b, 4), (c, 2), (d, 4)\}$
This is a function as no two pairs have the same first component.
(iii). $\{(a, 1), (a, 4), (b, 2), (c, 3), (d, 4)\}$
This is not a function as the elements $(a, 1)$ and $(a, 4)$ have the same first component.
(iv). $\{(a, 4), (b, 3), (c, 3), (d, 4)\}$
This is a function as no two pairs have the same first component.
(v). This is not a function as the element $c$ in the domain is not mapped to an element in the codomain.
End of Example 33.3. Functions as coordinate diagrams
In the previous section we demonstrated how a relation $f$, from a set $A$ to a set $B$, can be represented as a set of ordered pairs that is a subset of $A \times B$. We now plot these ordered pairs on a coordinate diagram of $A \times B$ with the domain values (inputs) on the horizontal axis and the range values (outputs) on the vertical axis. We know that for each input to a function there can only be exactly one output and so a vertical line through any given domain value must contain exactly one point.
Example
Draw the coordinate diagrams for each of the relations in Examples 2 and 3 and determine whether or not they represent functions.
Solution
Referring back to Examples 2 and 3 and treating each part of the question in turn.
(i) $f_1 = \{(a, 1), (b, 3), (c, 2), (d, 4)\}$
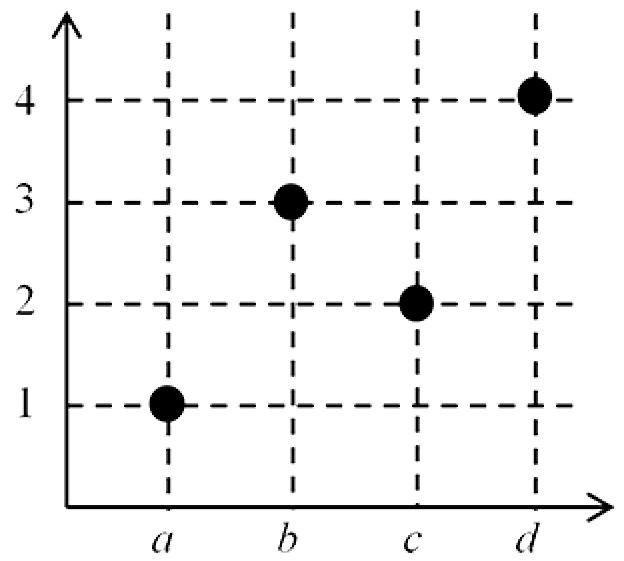
This is a function as each vertical line contains exactly one point of the set.
(ii) $f_2 = \{(a, 1), (b, 4), (c, 2), (d, 4)\}$
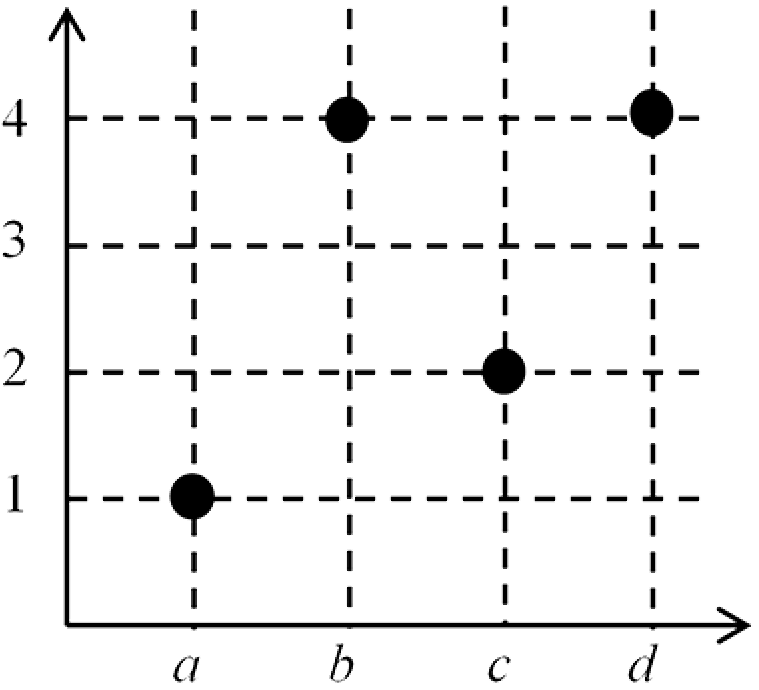
This is a function as each vertical line contains exactly one point of the set.
(iii) $f_3 = \{(a, 1), (a, 4), (b, 2), (c, 3), (d, 4)\}$
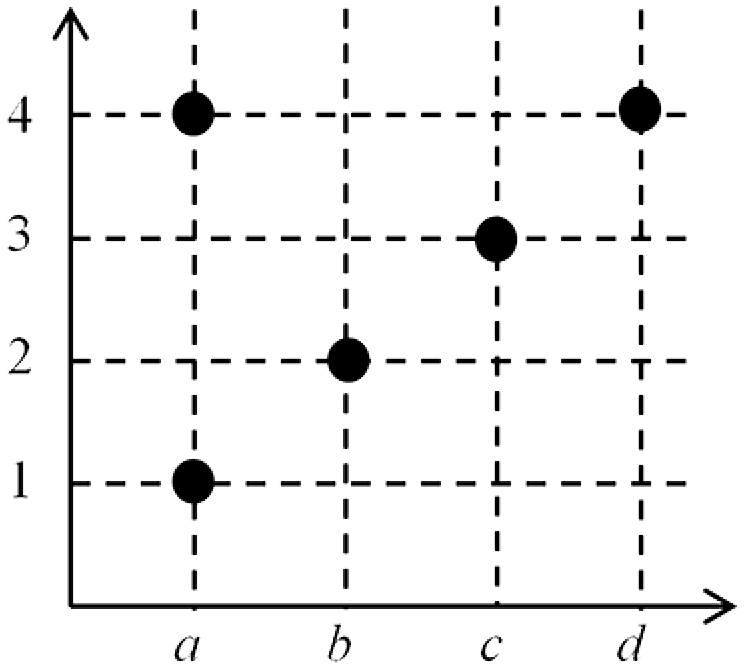
This is not a function as the vertical line through $a$ contains two points of the set.
(iv) $f_4 = \{(a, 4), (b, 3), (c, 3), (d, 4)\}$
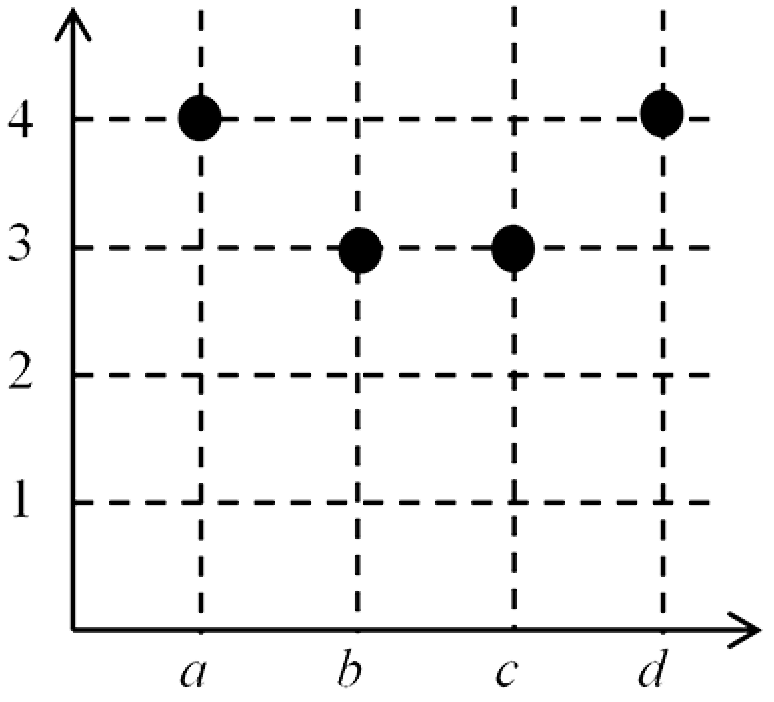
This is a function as each vertical line contains exactly one point of the set.
(v) $f_5 = \{(a, 1), (b, 2), (d, 4)\}$
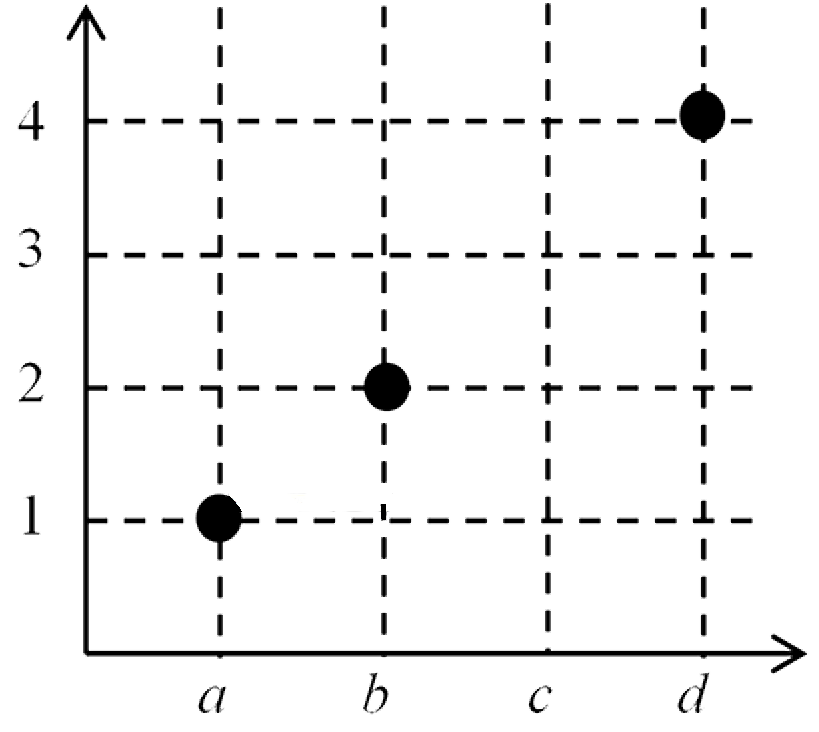
This is not a function as the vertical line through $c$ contains no point of the set.
End of Example3.4 Functions as equations and graphs
In previous units we demonstrated how a relationship between $x$ and $y$ coordinates in two-dimensional space can be represented by the formula, $y = f(x)$, and displayed graphically. Here we look at a relatively straightforward test, the Vertical Line Test, to determine whether or not a relationship is a function.
If a vertical line intersects the graph of $f$ at exactly one point for each $x$ then the relation is a function. Hence, a vertical line cannot intersect the graph of a function in more than one point.
The reason for this is that if a vertical line were to intersect the graph in more than one point then the same $x$-coordinate would correspond to more than one $y$-coordinate. Therefore a single value in the domain is mapped to more than one value in the range,violating the condition for a relation to be a function.
Example 4
(i). $y = x^2$ (ii). $y = \pm \sqrt{x}$
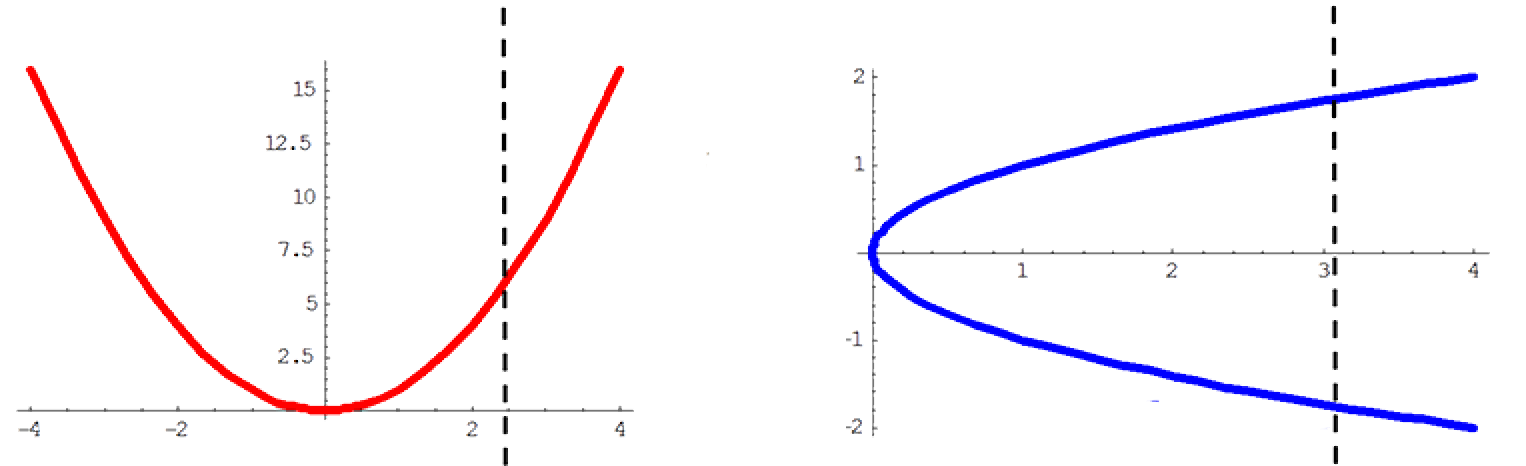
In the diagrams above:
(i). the line cuts the graph of $y = x^2$ in one point and so this is the graph of a function.
(ii). the line cuts the graph of $y = \pm \sqrt{x}$ in two points and so this is not the graph of a function.
We now introduce three very important classes of functions: injective functions, surjective functions and bijective functions.
End of Example 4 -
4. One-to-one functions
Further resources can be found at:
Surjective (onto) and injective (one-to-one) functions - (watch from 6:15 onwards)
Let $g : A \to B$ be a mapping from $A$ to $B$. We say that $g$ is one-to-one (also written $1-1$), or injective, if no two elements in $A$ have the same image in $B$. In other words each element in the domain of $g$ is mapped to exactly one element in the range of $g$.
In algebraic terms, a function $g$ is one-to-one if $g(a_1) = g(a_2)$ implies $a_1 = a_2$.
Alternatively a function $g$ is one-to-one if $a_1 \neq a_2$ implies $g(a_1) \neq g(a_2)$.
4.1. One-to-one functions as arrow diagrams
The following example shows how an arrow diagram can be used to determine whether a function, defining a relationship between two finite sets, is one-to-one.
Example 5
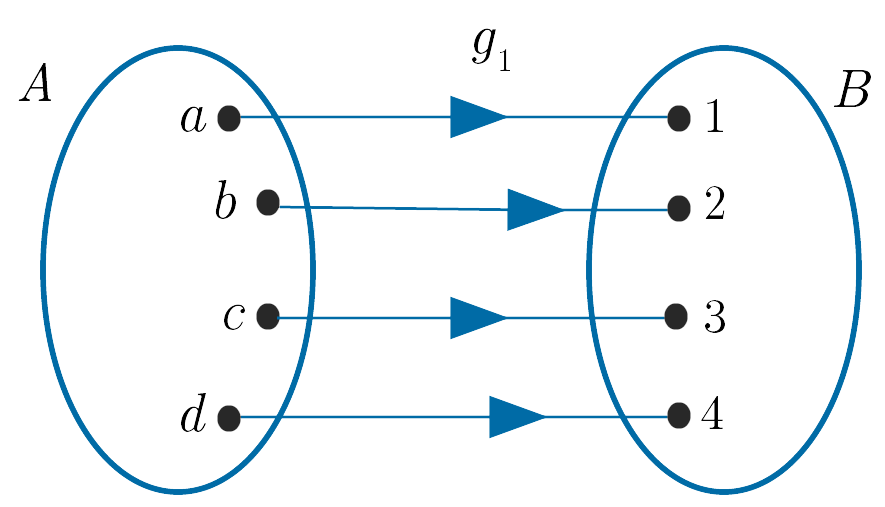
(i). $g_1 : A \to B$ is one-to-one as all the elements in $A$ have distinct images in $B$, i.e.
$g_1(a) = 1,\; g_1(b) = 2, \; g_1(c) = 3$ and $g_1(d) = 4$.
(ii). $g_2 : A \to B$ is not one-to-one as two elements in $A$ have the same image in $B$, i.e.
$g_2(a) = g_2(d) = 3$.
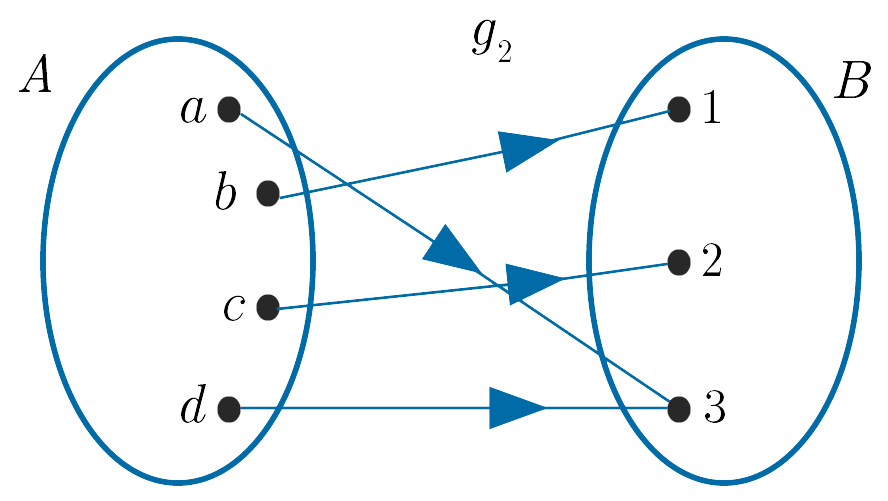
Note that if two, or more, elements of the domain $A$, are mapped to the same element of $B$ the function is said to be many-to-one.
(iii). $g_3 : A \to B$ is one-to-one as all the elements in $A$ have distinct images in $B$. It does not matter that the element $3$ in $B$ is not mapped to by an element of $A$.
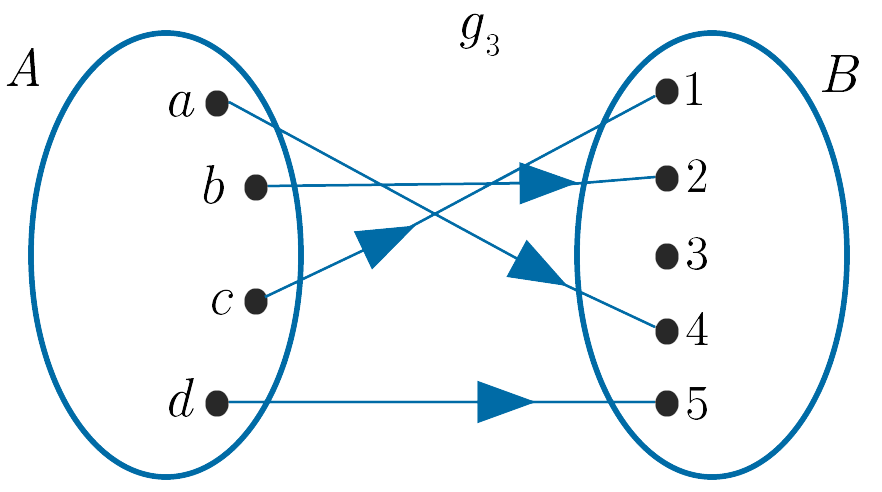 End of Example 5
End of Example 54.2. One-to-one functions as ordered pairs
By representing a function as a set of ordered pairs we can easily check if the function is one-to-one. If any elements in the set repeat the second component then we do not have a one-to-one function as this indicates different elements in the domain are mapped to the same element in the range thereby violating the one-to-one condition.
Example 6
Write each of the relations in Example 5 as a set of ordered pairs and determine whether or not they are one-to-one functions.
Solution
Referring back to Example 5 and treating each part of the question in turn.
(i). $\{(a, 1), (b, 2), (c, 3), (d, 4)\}$
(ii). $\{(a, 3), (b, 1), (c, 2), (d, 3)\}$
(iii). $\{(a, 4), (b, 2), (c, 1), (d, 5)\}$
Only (i) and (iii) represent one-to-one functions. Case (ii) includes ordered pairs with a repeated second component. Hence, different inputs produce the same output and this is not allowed for a one-to-one function.
End of Example 64.3. One-to-one functions as formulae and graphs
Given a function $f(x)$ we can sketch its graph and use the Horizontal Line Test to identify whether it is one-to-one.
If a function, $f(x)$, is one-to-one then no two distinct pairs $(a_1, b)$ and $(a_2, b)$ lie on the graph of $f$. Therefore any horizontal line can intersect the graph of $f$ in at most one point.
Example 7
(i). $f(x) = e^x$ is one-to-one as no horizontal line intersects the curve in more than one point.
(ii). $g(x) = x^2 + x^3$ is not one-to-one as some horizontal lines cut the graph of $g(x)$ in more than one point.
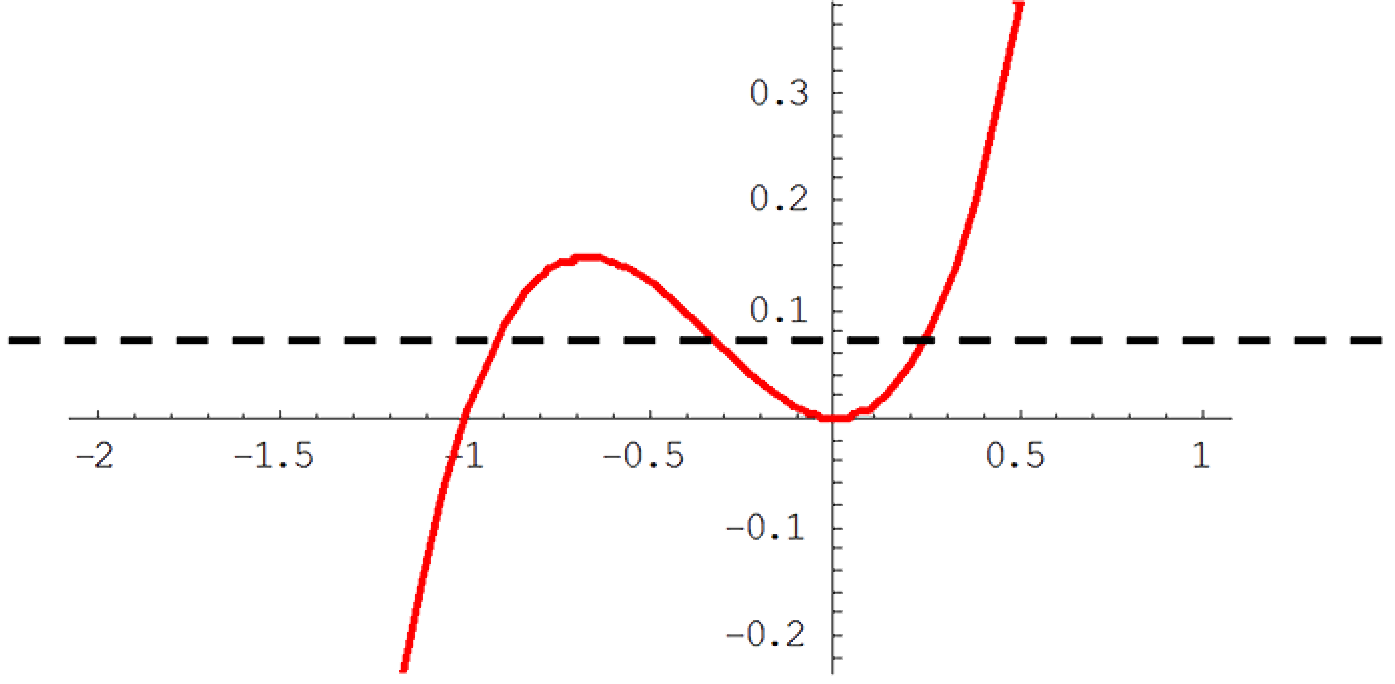 End of Example 7
End of Example 74.4. Identifying one-to-one functions algebraically (OPTIONAL)
To prove that a function $f$ is one-to-one algebraically we use the property that $f$ is one-to-one if $f(a_1) = f(a_2)$ implies $a_1 = a_2$.
Example 8
Determine if the following functions are one-to-one:
(i). $f(x) = \frac{1}{x}, x \neq 0$.
(ii). $g(x) = x - x^3$
Solution
(i). Let $a_1$ and $a_2$ be any two real numbers such that $f(a_1) = f(a_2)$.
We need to show that $a_1 = a_2$.
Now $f(a_1) = \frac{1}{a_1}$ and $f(a_2) = \frac{1}{a_2}$.
Then $\frac{1}{a_1} = \frac{1}{a_2}$ gives that $a_1 = a_2$ proving that $f(x)$ is one-to-one.
(ii). We have $g(x) = x^2 - x^3 = x^2(1 - x)$.
We shall prove $g$ is not one-to-one by giving a counterexample.
If we can find two different elements in the domain that map to the same element then we have shown that the function is not one-to-one.
Let $a_1 = 0$ and $a_2 = 1$. Then
$g(0) = 0(1 - 0) = 0$ and
$g(1) = 1(1 - 1) = 0$.
Hence, $g(a_1) = g(a_2) = 0$, i.e. both $0$ and $1$ in the domain map to 0 in the range.
However, $a1 \neq a2$ and so $g(x)$ is not one-to-one.
End of Example 8 -
5. Onto functions
Further resources can be found at:
Surjective (onto) and injective (one-to-one) functions- (watch up to 6:15)
Let $h : A \to B$ be a function from $A$ to $B$. We say that $h$ is onto, or surjective, if each element in $B$ is the image of at least one element of $A$.
5.1. Onto functions as arrow diagrams
The following example shows how an arrow diagram can be used to determine whether a function, defining a relationship between two finite sets, is onto.
Example 9
(i). $h_1 : A \to B$ is onto as every element in $B$ is mapped to some element of $A$.
The range of $h_1, \{1, 2, 3\}$, is the same as the codomain of $h_1$.
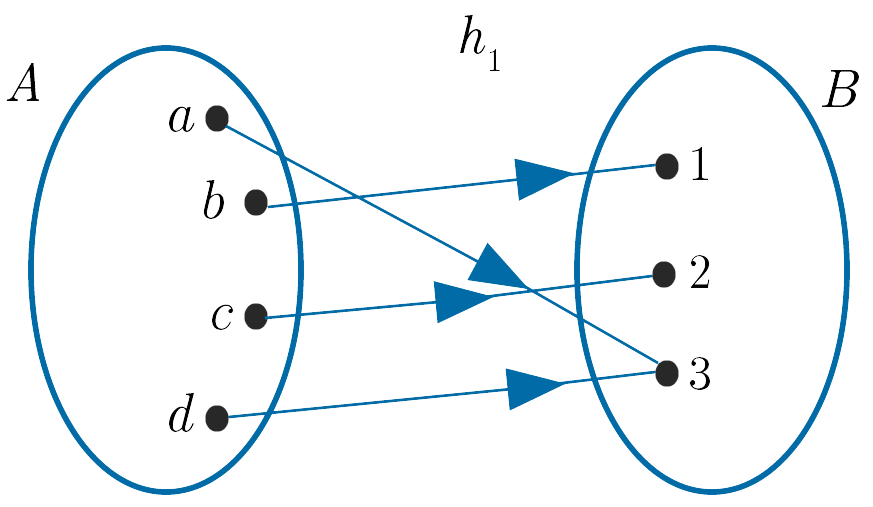
(ii). $h_2 : A \to B$ is not onto as the element $3$ in $B$ is not the image of an element of $A$.
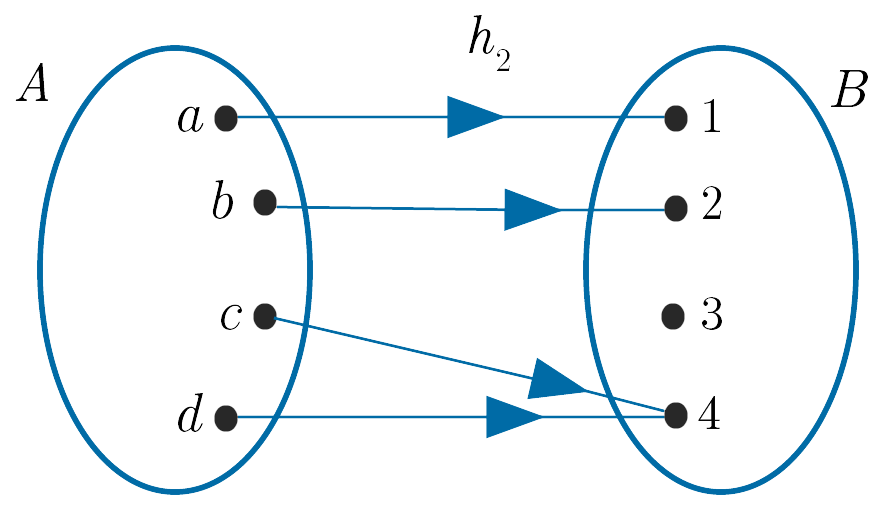
The range of $h_2, \{1, 2, 3\}$, is not the same as the codomain of $h_2, \{1, 2, 3, 4\}$.
End of Example 95.2. Onto functions as formulae and graphs
If a function $f: A \to B$ is onto then for every $b \in B$ there must be at least one $a \in A$ such that $(a,\; b)$ lies on the graph of $f$.
Therefore any horizontal line must intersect the graph of $f$ at least once
Example 10
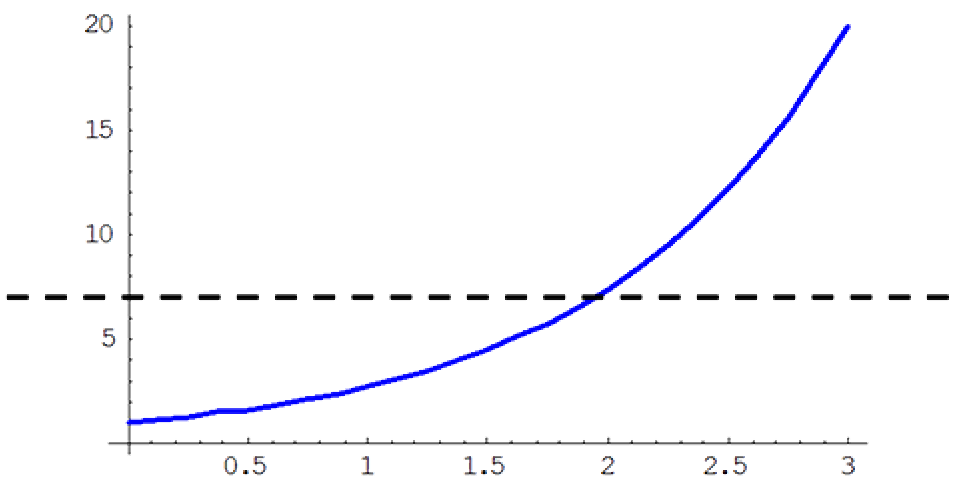
The function $f : \mathbb{R} \to \mathbb{R}$ defined by, $f(x) = e^x$ is not onto as there are horizontal lines that do not intersect the curve. For example, the dashed line in the diagram does not intersect $f(x)$.
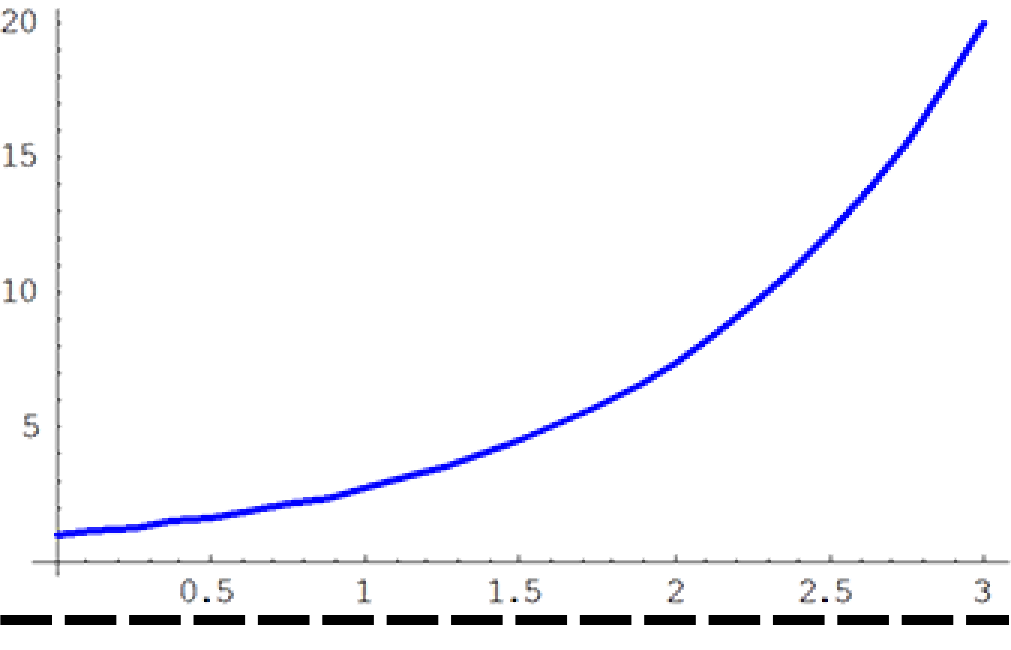
Note here that the domain and codomain both include all the real numbers. However, the function $e^x$ will always be positive and this is a problem as there are values in the codomain of $f$ that are not in the range of $f$ . Hence, $f(x) = e^x$ cannot be an onto function.
If however the codomain was restricted to the interval $(0, \; \infty)$ then the function is onto (and one-to-one).
End of Example 105.3. Identifying onto functions algebraically (OPTIONAL)
To prove that a function $f$ is onto algebraically we need to show that for every element in the codomain there is an element in the domain which maps to it.
Example 11
Determine whether the following functions are onto.
(i). $f(x) = 3x - 4 \; \text{where} \; f : \mathbb{R} \to \mathbb{R}$.
(ii). $g(x) = x + 2 \; \text{where} \; g: \mathbb{Z}^+ \to \mathbb{Z}^+$. (Note that $\mathbb{Z}^+$ is the set of positive integers)
Solution
(i). Let $y \in \mathbb{R}$ be any element in the codomain.
We need to show that there is an $x \in \mathbb{R}$ (the domain) such that $f(x) = y$.
We have $y = 3x - 4$ so
$x = {\Large\frac{y + 4}{3}}$ is a real number, since $y$ is real, in the domain.
Now try to show that $f(x) = y$, i.e.
$$f\Bigg(\frac{y + 4}{3}\Bigg) = 3\Bigg(\frac{y + 4}{3}\Bigg) - 4$$
$= y + 4 - 4$
$= y$.
As we have found an element that maps to $y$ we have proved that $f$ is onto.
This is a relatively straightforward example as in general it can be much harder to prove algebraically that a function is onto than it is to prove a function is one-to-one.
(ii). We show this function is not onto using a counterexample.
If $g(x) = x + 2 = 2$ then we must have that $x = 0$.
However, $0$ is not a positive integer and therefore not in the domain of $g$.
Hence, the element 2 in the codomain is not mapped to by any element of the domain and we conclude that $g$ is not onto.
End of Example 11 -
6. One-to-one and onto functions
A function $f : A \to B$ that is both one-to-one and onto (i.e. a one-to-one correspondence) is said to be bijective.
6.1. One-to-one and onto functions as arrow diagrams
An arrow diagram can be used to determine whether a function, defining a relationship between two finite sets, is bijective. The procedure is illustrated in the following example.
Example 12
(i). $f : A \to B$ is bijective as it is one-to-one, no element of $B$ is the image of more than one element of $A$, and it is onto as every element in $B$ is the image of some element of $A$.
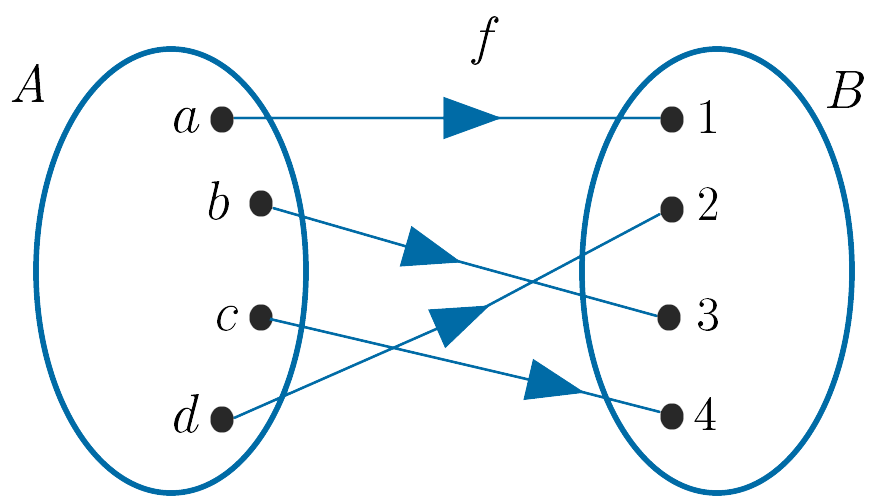
(ii). $g : A \to B$ is one-to-one but not onto as the element $3$ in $B$ is not mapped to some element of $A$.
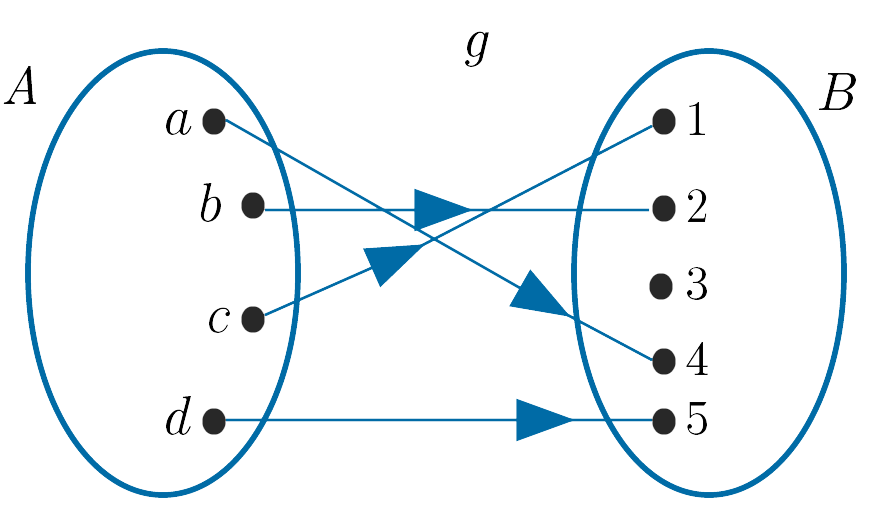
(iii). $h : A \to B$ is onto but not one-to-one as the element $3$ in $B$ is the image of two elements, $c$ and $d$, in $A$.
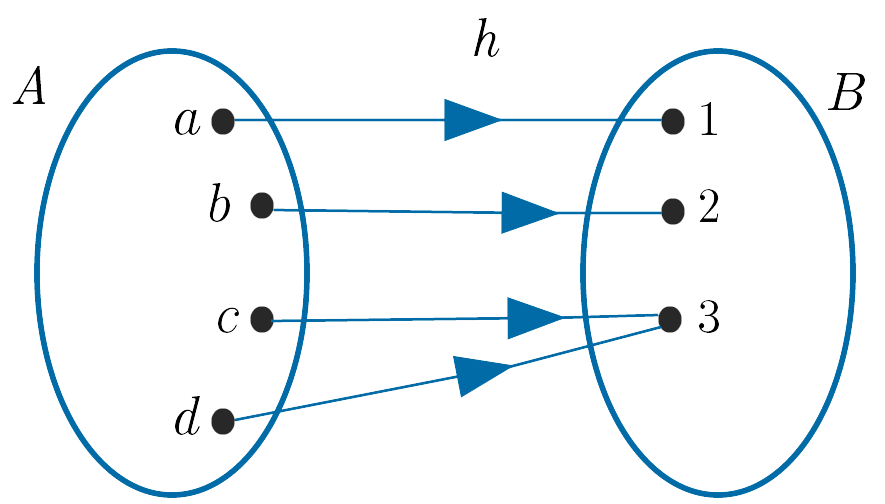
(iv). $k : A \to B$ is neither one-to-one nor not onto.
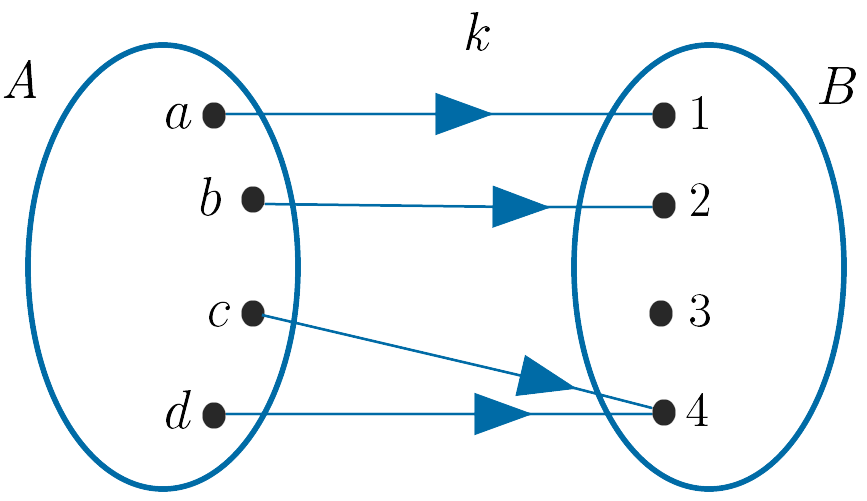
It is not one-to-one as the element $4$ in $B$ is the image of two elements in $A$.
It is not onto as the element $3$ in $B$ is not mapped to by some element of $A$.
End of Example 12 -
7. Inverse Functions
Further reading on this topic is available at the following links
A function $f : A \to B$ has an inverse $B \to A$ if and only if it is both one-one and onto (bijective). In other words, $f : A \to B$ is invertible if its inverse, written $f^{-1}$, is a function from $B$ to $A$.
7.1. Inverse functions and arrow diagrams
The arrow diagram shows a bijective function $f$ from the set $A$ to the set $B$. The inverse function, $f^{-1}$, from $B$ to $A$ is also shown and is obtained by simply reversing the arrows.
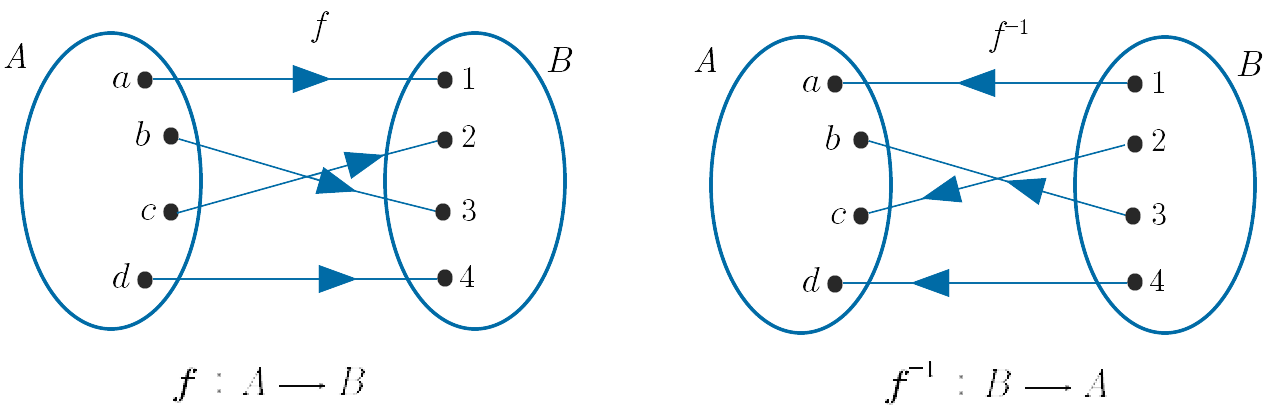
Note that the roles of the domain and range are interchanged. The domain of $f$ (the set $A$) is the range of $f^{-1}$ and the range of $f$ (the set $B$) is the domain of $f^{-1}$.
Example 13
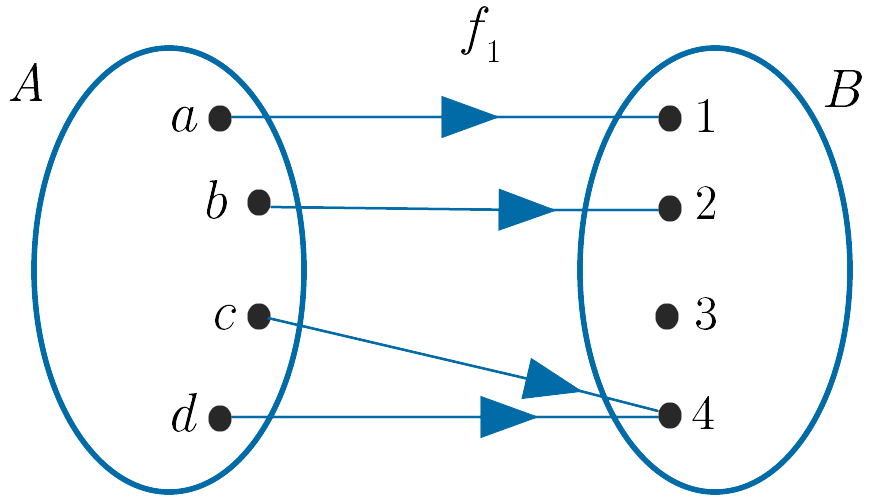
Which of the following functions have an inverse?
(i).
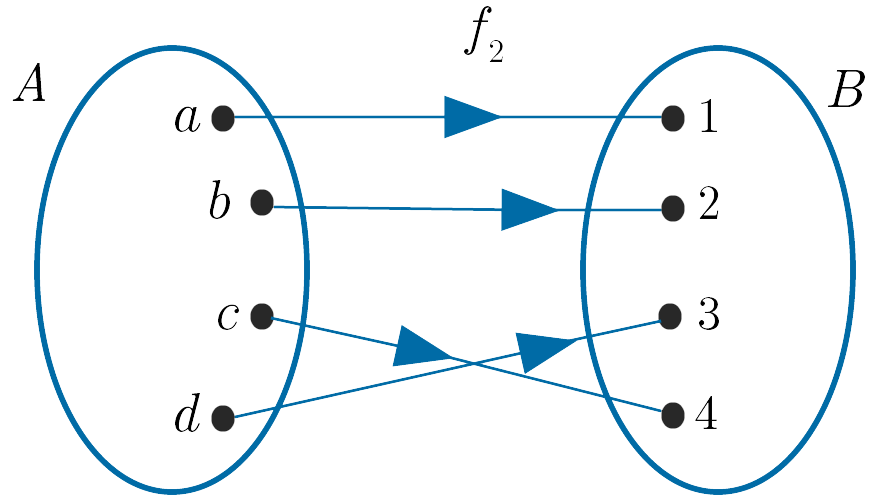
(ii).
(iii).
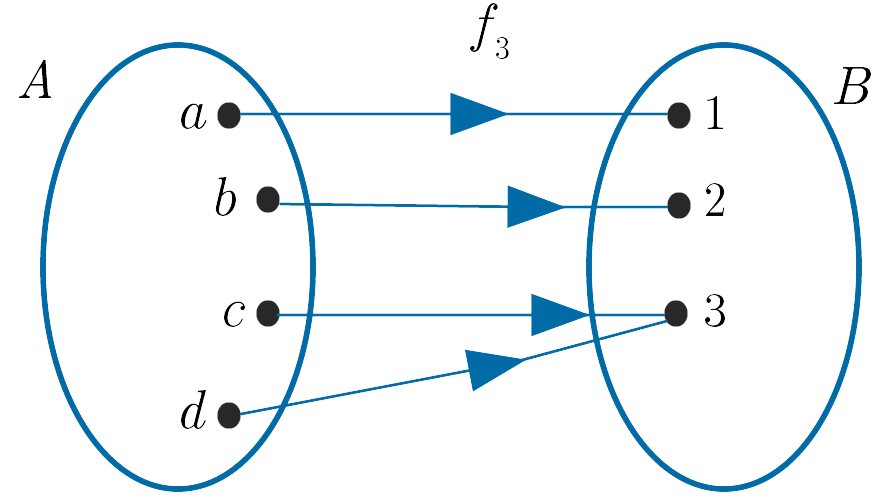
Solution
For a function to have an inverse it must be both one-to-one and onto. Only the function $f_2$ , shown in (ii), is one-to-one and onto and so only $f_2$ has an inverse. The function in (i) is neither one-to-one nor onto, while (iii) is onto but not one-to-one.
End of Example 137.2. Identifying inverse functions algebraically
An algebraic proof that a function is invertible involves applying the so-called “solve and switch” method to the function equation.
Example 14
(i). Let $f : \mathbb{R} \to \mathbb{R}$ be defined by, $f(x) = 4x - 7$.
Determine the inverse function, $f^{-1}(x)$
Solution
Rewrite as: $y = 4x - 7$
Solve for $x$: $x = {\Large\frac{y + 7}{4}} = f^{-1}(y)$
Switch $x$ and $y$ to obtain the inverse: $y = {\Large\frac{x + 7}{4}} = f^{-1}(x)$.
So $f^{-1} : \mathbb{R} \to \mathbb{R}$ is defined by, $f^{-1}(x) = {\Large\frac{x + 7}{4}}$.
Note: If a point $(x,\; y)$ lies on the graph of a function then the point $(y,\; x)$ must lie on the graph of its inverse. For example, it is easily shown here that the point $(2, 1)$ lies on the graph of $f(x)$ and that the point $(1, 2)$ lies on the graph of its inverse $f^{-1}(x)$.
(ii). Let $f(x) = {\Large\frac{x + 6}{x - 3}},\; x \neq 3$. Determine the inverse function, $f^{-1}(x)$.
(Note that the condition $x \neq 3$ is included to avoid division by zero).
Solution
Rewrite as: $y = {\Large\frac{x + 6}{x - 3}}$
Solve for $x$: $y(x - 3) = x + 6$
$xy - 3y = x + 6$
$xy - x = 3y + 6$
$x(y - 1) = 3(y + 2)$
$x = {\Large\frac{3(y + 2)}{(y - 1)}} = f^{-1}(y), \; (y \neq 1)$
Switch $x$ and $y$ to obtain the inverse $y = {\Large\frac{3(x + 2)}{(x - 1)}} = f^{-1}(x), \; x \neq 1$.
Hence, the inverse here is, $f^{-1}(x) = {\Large\frac{3(x + 2)}{x - 1}}, \; x \neq 1$.
Note:
- The condition $x \neq 1$ avoids division by zero.
- Check: the point $(6,\; 4)$, say, lies on the graph of $f(x)$ and we can easily show that the point $(4,\; 6)$ lies on the graph of $f^{-1}(x)$.
End of Example 147.2.1. Function notation
To fully define a function $f$ algebraically we must state the domain and codomain as well as the formula that represents the function. If $A$ and $B$ are sets then a mapping from $A$ to $B$ can be written as
$f : A \to B$
$x \mapsto f(x)$
Referring to Example 14(ii) we would write the following:
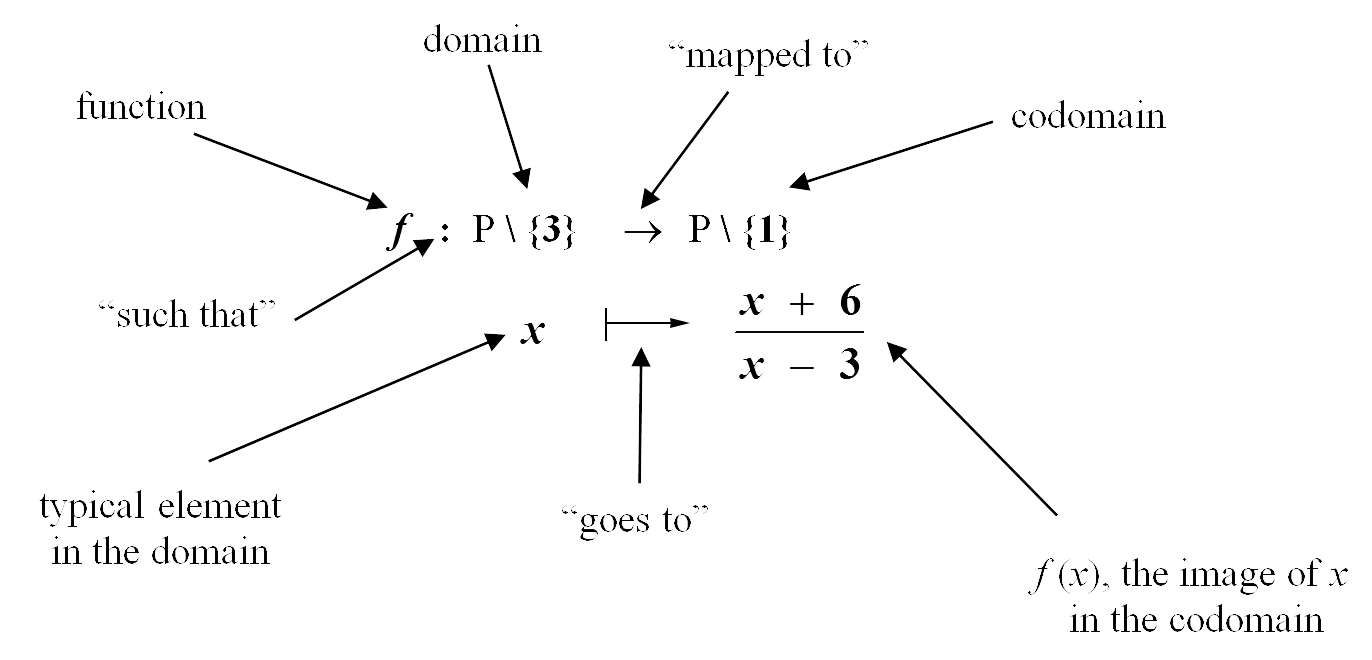
The term $\mathbb{R}$ \ $\{3\}$ indicates that the domain of $f$ is the real numbers with $3$ excluded.
The term $\mathbb{R}$ \ $\{1\}$ indicates that the codomain of $f$ is the real numbers with $1$ excluded.
Similarly, the inverse function is written as
$f^{-1} : \mathbb{R}$ \ $\{1\} \to \mathbb{R}$ \ $\{3\}$
$x \mapsto {\Large\frac{3(x + 2)}{x - 1}}$
The term $\mathbb{R}$ \ $\{1\}$ indicates that the domain of $f^{-1}$ is the real numbers with $1$ excluded.
The term $\mathbb{R}$ \ $\{3\}$ indicates that the codomain of $f^{-1}$ is the real numbers with $3$ excluded.
Example 15
In Unit 4 we described how the logarithmic and exponential functions are inverses of each other.
We illustrate with examples.
(i). Find the inverse of the function $f(x) = log_2(x - 4)$.
Note here that we must have $x > 4$ to ensure that we are taking the log of a strictly positive number.
Solution
Rewrite as: $y = log_2(x - 4)$
Solve for $x$: $2^y = 2^{log_2(x-4)}$
$2^y = x - 4$
$x = 2^y + 4 = f^{-1}(y)$
Switch $x$ and $y$ to obtain the inverse: $y = 2^x + 4 = f^{-1}(x)$.
Hence, the inverse here is, $f^{-1}(x) = 2^x + 4$.
Check: It is easily shown that the point $(5,\; 0)$, say, lies on the graph of $f(x)$ and that the point $(0,\; 5)$ lies on the graph of $f^{-1}(x)$.
(ii). Find the inverse of the function $f(x) = e^{3x-2}$.
Solution
Rewrite as: $y = e^{3x - 2}$
Solve for $x$: $ln(y) = ln(e^{3x-2})$
$ln(y) = 3x - 2$
$x = {\Large\frac{1}{3}}[ln(y) + 2] = f^{-1}(y)$
Switch $x$ and $y$ to obtain the inverse: $y = {\Large\frac{1}{3}}[ln(x) + 2] = f^{-1}(x), \; (x > 0)$.
Hence, the inverse here is, $f^{-1}(x) = {\Large\frac{1}{3}}[ln(x) + 2], \; (x > 0)$.
Note:
- The condition $x > 0$ ensures we are taking the natural log of a strictly positive value.
- Check: it is easily shown that the point $(1, \;e)$ lies on the graph of $f(x)$ and that the point $(e,\; 1)$ lies on the graph of $f^{-1}(x)$.
End of Example 15Example 16
Let $g : \mathbb{R} \to \mathbb{R}$ be defined by, $g(x) = x^2$. Does $g$ have an inverse?
Solution
The function, $g : \mathbb{R} \to \mathbb{R}$ given by $g(x) = x^2$ is neither one-to-one nor onto and therefore does not have an inverse.
It is not one-to-one as, for example, $g(-2) = g(2) = 4$, i.e. the number $4$, in the range, is the image of more than one number in the domain.
It is not onto as the range of $g(x)$ is $[0, \; \infty)$ . For example, there is no number $x \in \mathbb{R}$, such that $x^2 = -1$.
Note that if we restrict the domain to strictly non-negative values of $x$, i.e. $x \ge 0$, then the function $g(x) = x^2$ will be both one-to-one and onto and therefore have an inverse. In this case $g^{-1}(x) = + \sqrt{x}$.
Similarly we could define $g(x)$ for $x \le 0$ to obtain $g^{-1}(x) = - \sqrt{x}$.
End of Example 167.3. Identifying inverse functions graphically – Horizontal Line Test
A function, $f$ , is both one-to-one and onto, and hence, invertible if and only if any horizontal line intersects the graph of $f$ in exactly one point.
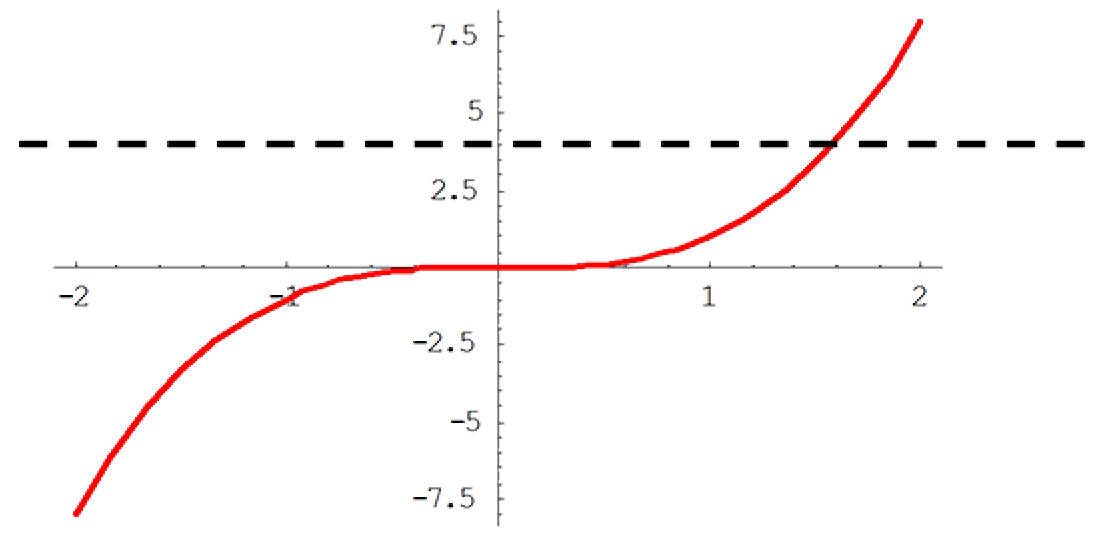
The function, $f : \mathbb{R} \to \mathbb{R}$ given by $f(x) = x^3$ is invertible as any horizontal line will intersect the graph of $f$ exactly once. See dashed line in the diagram.
Exercise: Show that the inverse function, $f^{-1}(x) = x^{1/3}$.
7.3.1. Plotting a function and its inverse (OPTIONAL)
As we have seen the difference between a function and its inverse is that all the $x$ and $y$ coordinates are switched. In other words if $(x,\; y)$ is a point on the graph of $f(x)$ then $(y,\; x)$ is a point on the graph of $f^{-1}(x)$.
The graph of a function and its inverse are mirror images of each other in the line $y = x$.
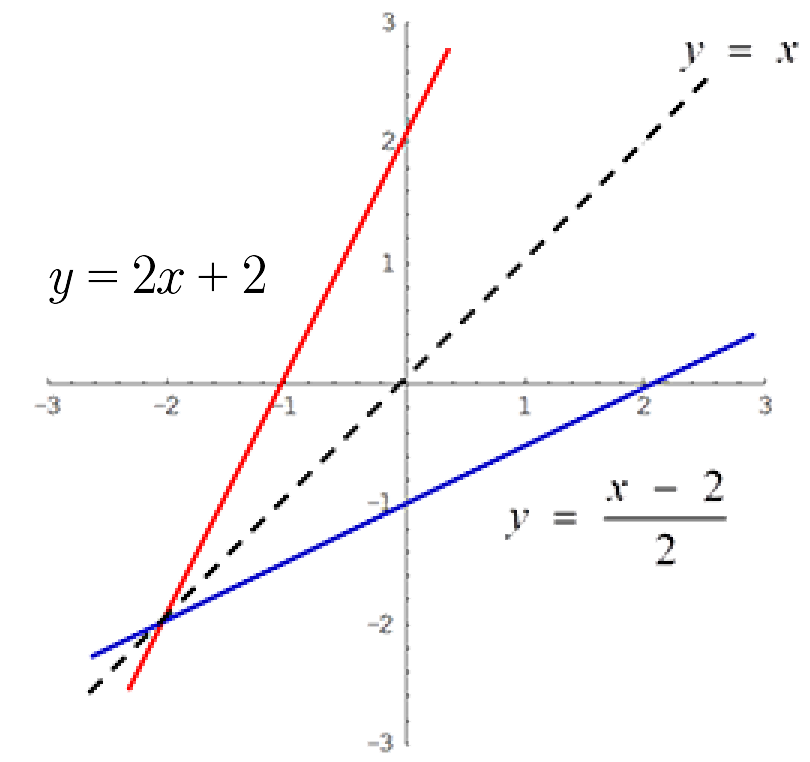
Example 17
As a simple example, let $f : \mathbb{R} \to \mathbb{R}$ be defined by, $f(x) = 2x + 2$.
The inverse can be shown to be given by $f^{-1}(x) = {\Large\frac{x - 2}{2}}$.
Both functions are shown in the diagram. The graph of $f(x)$ and $f^{-1}(x)$ are symmetric across the line $y = x$.
 End of Example 17
End of Example 17 -
8. Composition of functions
Further reading on this topic is available at the following links:
Consider the two functions $f : A \to B$ and $g : B \to C$
The composition of $g$ and $f$, written $g \; o \; f$ , is the function from $A$ to $C$ where
$( g \; o \; f)(x) = g(f(x))$.
Diagrammatically the composition $g\; o\; f : A \to C$ is shown below. First we apply the function $f$ to the element $x$ in $A$. The resulting output, $f(x)$, is the input to $B$. Then we apply the function $g$ to $f(x)$ to obtain $g( f(x))$ in $C$.
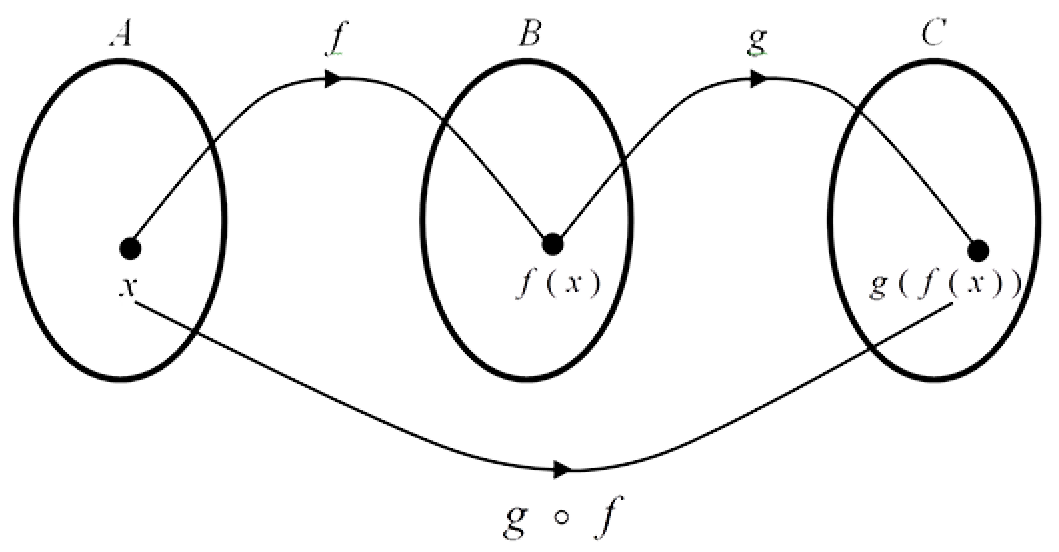
The composition $f o g$ where we apply $g$ first followed by $f$ can defined in an analogous manner.
Note that the order in which we compose functions is important and it is rarely the case that the composition of $g$ and $f$ , i.e. $g o f$ is equal to the composition of $f$ and $g$, i.e. $f o g $.
8.1. Composition of functions and arrow diagrams
The following example shows how an arrow diagram can be used to determine the composition of two functions.
Example 18
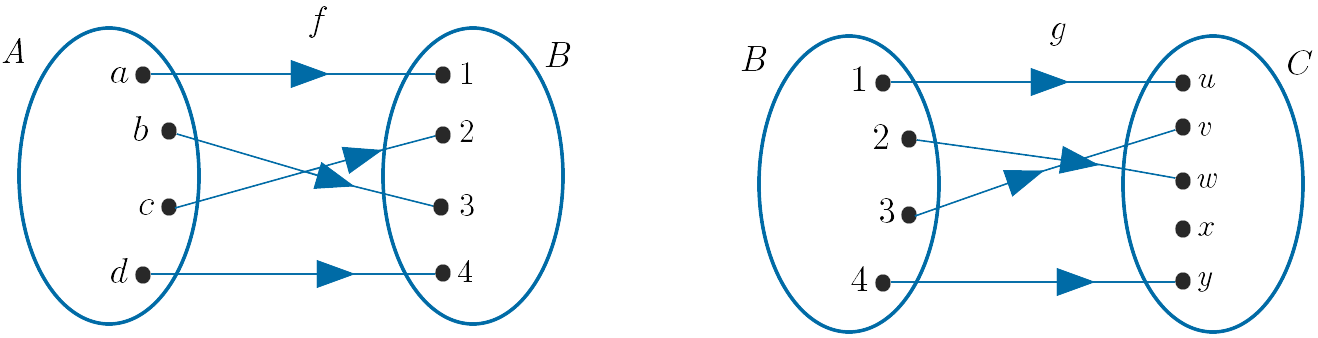
Let $A = \{a, b, c, d\}, B = \{1, 2, 3, 4\}$ and $C = \{u, v, w, x, y\}$ and define the functions $f : A \to B$ and $g : B \to C$ as shown below.
Determine the composition $g \;o\; f$ and state the domain and range of $g \;o\; f$.
Solution
To evaluate $g \;o\; f$ we apply $f$ first followed by $g$ giving the following paths from $A$ to $C$.
$a \to 1 \to u, \; b \to 3 \to v, \; c \to 2 \to w, \; d \to 4 \to y$.
Combining the above gives:
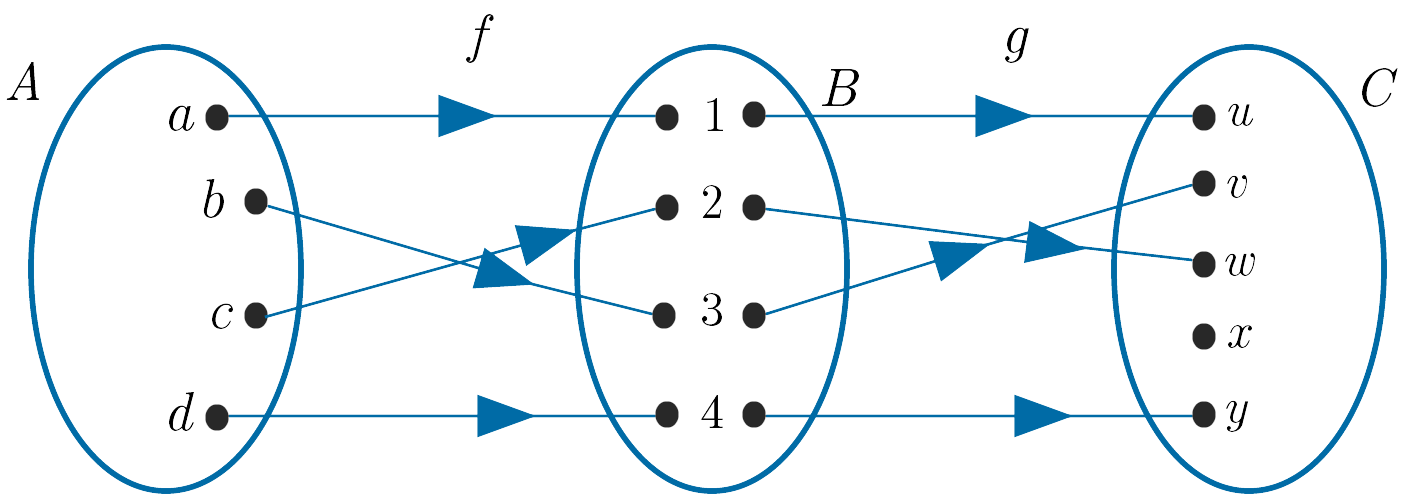
For example, we have a path from $a$ in $A$ to $u$ in $C$, a path from $b$ in $A$ to $v$ in $C$, etc.
The relationship generated by the composite function is shown below.
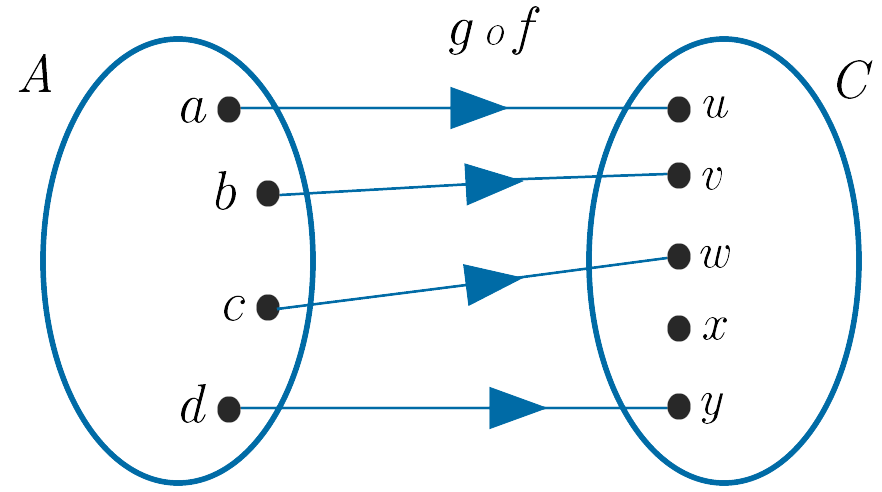
The domain of $g \;o\; f$ is $\{a, b, c, d\}$ and the range is $\{u, v, w, y\}$.
Note:
- If $f$ and $g$ are both one-to-one functions then $g \;o\; f$ is one-to-one. See Example 18 above where both functions are one-to-one.
- If $f$ and $g$ are both onto functions then $g \;o\; f$ is onto.
End of Example 188.2. Composing functions algebraically
The composition of two functions $g$ and $f$ is obtained using the following equation,
$(g\; o\; f)(x) = g( f (x))$.
The entire function $f$ is substituted into $g$ to create the new composite function $g( f (x))$.
Example 19
Let $f$ and $g$ be functions, $\mathbb{R} \to \mathbb{R}$, defined as $f(x) = x + 3$ and $g(x) = 2x - 7$.
(i). Determine $g \;o\; f$ and verify your answer.
(ii). Determine $f \;o\; g$ and verify your answer.
Solution
(i). $(g \; o \; f)(x) = g(f(x))$
$= g(x + 3)$
$= 2(x + 3) - 7$
$=$ $\;2x\;-\;1$.
Verification: We should be able to take an arbitrary value of $x$, substitute it in $g \;o\; f$ and obtain the same result as if we were to first evaluate $f(x)$ at the chosen $x$ value and use the result as input to $g(x)$.
For example, choose $x = 2$ so that
$(g \;o\; f)(2) = 2 \times 2 - 1 = 3$.
Also, $f(2) = 2 + 3 = 5$. Using this value as input to $g$ gives, $g(5) = 2 \times 5 - 7 = 3$.
This is the same as the result obtained above for $(g\; o\; f)(2)$.
(ii). $(f \;o\; g)(x) = f(g(x))$
$= f(2x - 7)$
$= 2x - 7 + 3$
$=$$\;2x\; -\; 4$.
Note that $g\; o\; f \neq f\; o\; g$.
Verification:
Choose $x = 2$ so that
$(f\; o\; g)(2) = 2 \times 2 - 4 = 0$
Also, $g(2) = 2 \times 2 - 7 = -3$.
Using this value as input to $f$ gives, $f(-3) = -3 + 3 = 0$.
This is the same as the result obtained above for $(f\; o\; g)(2)$.
End of Example 19Example 20
Let $f$ and $g$ be the functions, $\mathbb{R} \to \mathbb{R}$ defined as $f(x) = 3x - 4$ and $g(x) = x^2 + 2$.
Determine $g\; o\; f$ and $f\; o\; g$.
Solution
$(g\;o\;f)(x) = g(f(x))$$(f\; o\; g)(x) = f(g(x))$
$= g(3x - 4)$ $= f(x^2 + 2)$
$= (3x - 4)^2 + 2$ $= 3(x^2 + 2) -4$
$=$$\;9x^2 - 24x + 18$. $=$$\;3x^2 + 2$.
Clearly $g\; o\; f \neq f\; o\; g$.
In the examples given above we were able to compose the functions for all values of $x$. However, there are some pairs of functions that cannot be composed while some pairs can only be composed for specific values of $x$.
End of Example 20Example 21
(i). Let $f(x) = - x^2$ and $g(x) = ln(x)$.
Show that the composite function $g \;o\; f$ does not exist.
Solution
First we note that $f(x) \le 0$ for all values of $x$ and that $g(x)$ is only defined for $x > 0$. Proceeding in the usual manner we have ,
$(g\; o\; f)(x) \;\;= g(f(x))$
$= g(-x^2)$
$= ln(-x^2)$.
This term however cannot be evaluated as the natural logarithm of a non-positive expression is not defined $(-x^2 \le 0$ for all $x$). Hence, the composite function $g\; o\; f$ does not exist.
(ii). Let $f(x) = x -1$ and $g(x) = \sqrt{x}$.
Determine the composite function $g \;o\; f$ and state any values for which it is undefined.
Solution
Note here that $f(x)$ is defined for all values of $x$ while $g(x)$ is only defined for $x \ge 0$. Proceeding in the usual manner we have,
$(g\; o\; f) \;\;= g(f(x))$
$= g(x - 1)$
$= \sqrt{x - 1}$
which is only valid for $x \ge 1$.
Hence, the composite function $(g\; o\; f)$ only exists for $x \ge 1$.
End of Example 218.3. The composition of a function and its inverse (OPTIONAL)
To prove that two functions are inverses of each other we compose the functions.
In general, applying a function, $f$ to some value $x$ and then applying the inverse function, $f^{-1}$, to the result will recover the original $x$. Hence,
$f^{-1}( f (x)) = x$.
Similarly, changing the order in which the functions $f$ and $f^{-1}$ are applied has the same effect, i.e.
$ f ( f^{-1} (x)) = x.$
Example 22
In Example 14 we found that the function $f(x) = 4x - 7$ has inverse $f^{-1}(x) = {\Large\frac{x + 7}{4}}$
We now prove this result by composing the functions:
$(f^{-1}\; o\; f)(x) \;\; = f^{-1}(f(x))$
$= f^{-1}(4x - 7)$
$= {\Large\frac{4x - 7 + 7}{4}}$
$= x$.
Similarly,
$(f\; o\; f^{1})(x) \;\; = f(f^{-1}(x))$
$= f \Big({\Large\frac{x + 7}{4}}\Big)$
$= 4 \Big({\Large\frac{x + 7}{4}}\Big) - 7$
$= x + 7 - 7$
$= x$.
Hence, $f(x) = 4x - 7$ and $f^{-1}(x) = {\Large\frac{x + 7}{4}}$ are inverses of each other.
End of Example 22 -
9. Functions in Computing
There are many mathematical functions that appear in software packages such as Matlab, and Maple and in programming languages such as C++. The JavaScript Math Object lists some commonly used functions at this link
ROUND : $\mathbb{R} \to \mathbb{Z}$
ROUND$(x)$ rounds to the nearest integer. Half-integer values are rounded to even numbers.
ROUND$(2.3) = 2$, ROUND$(4.7) = 5$, ROUND$(2.5) = 2$, ROUND$(3.5) = 4$.
INT : $\mathbb{R} \to \mathbb{Z}$
INT$(x)$, converts x into an integer by removing the fractional part of the number $x$.
INT$(6.3) = 6$, INT$(2.9) = 2$, INT$(3.7) = 3$.
FLOOR : $\mathbb{R} \to \mathbb{Z}$
FLOOR $(x)$ rounds $x$ to the nearest integer towards minus infinity.
FLOOR$(-9.3) = -10$, INT$(7.9) = 7$.
CEIL : $\mathbb{R} \to \mathbb{Z}$
CEIL$(x)$ rounds $x$ to the nearest integer towards plus infinity.
CEIL$(-4.9) =\; ̶ \; 4$, INT$(6.7) = 7$.
ASCII : $\{A, B, C, ..., Z\} \to \{65, 66, 67, ..., 90\}$.
ASCII $(x)$ returns the integer ASCII code for the character $x$.
ASCII$(A) = 65$, ASCII$(B) = 66$.
CHR : ${65, 66, 67, ..., 90} \to {A, B, C, ..., Z}$
CHR $(x)$ takes an integer as its argument and returns a string consisting of one character having an ASCII code as given by $x$.
CHR$(65) = A$, CHR$(66) = B$, CHR$(90) = Z$.
-
Summary
- In this unit we have introduced the concept of a function and you should now be able to:
- understand what is meant by the term function.
- understand the concepts of domain, codomain, image and range.
- represent functions as arrow diagrams, ordered pairs, equations and graphically.
- identify whether a relation in the form of an arrow diagram, or a set of ordered pairs or in equation form is a function.
- use the Vertical Line Test to determine whether a relation is a function.
- understand what it means for a function to be one-to-one.
- understand what it means for a function to be onto.
- understand what it means for a function to have an inverse.
- determine whether a function has an inverse.
- apply the Horizontal Line Test to identify if a function has an inverse.
- calculate the composition of two functions and identify the domain and range of the composite function.
You should now attempt the tutorial exercises and Maple Questions on GCU Learn.
The next unit presents binary relations on sets.