-
1. Introduction
In this final unit of the current block we introduce the mathematical concept of relations between sets. We look at how relations differ from functions while noting that a function is actually a special type of relation. Different ways in which relations can be represented are discussed and include ordered pairs, arrow diagrams, matrices and directed graphs. Inverse and composite relations are briefly addressed before we investigate different types of relations (reflexive, symmetric and transitive) and methods for their classification. The important concepts of equivalence relations and equivalence classes are then described along with their properties. In closing the unit we look at the connection between equivalence relations and partitions of sets. The text is supported throughout with relevant examples and where appropriate references for further reading are provided.
1.1. Some basics
We are all familiar with the many types of relations that occur in mathematics and computing, e.g. “is equal to”, “is greater than”, “is a member of”, as well as those relations that occur in everyday life, e.g. “is the daughter of”, “is the husband of”, “plays football for”, and so on. The common thread in all of these relations is that they represent an association between two numbers or objects from different sets and are therefore called binary relations.
Suppose we are interested in finding out how many teams have won the European Champions league football competition since it started in season 1992/93 and how many times each team has won the cup. A total of 13 teams have won the completion in the 27 years since it started, ranging from several teams with a single win to one team that has recorded 7 championships. We could define a set $A$ to be the set of all teams that have won the competition and a set $B$ to include the values from 1 to 7 corresponding to the number of wins. Hence, the “team/cup wins” relation, which we denote by $R$, can be thought of as a relation from $A$ to $B$.
Here the sets $A$ and $B$ are defined as follows:
$A = ${Marseilles, AC Milan, Ajax Amsterdam, Juventus, Borussia Dortmund, Real Madrid, Manchester United, Bayern Munich, Porto, Liverpool, Barcelona, Chelsea, Inter Milan }
and
$B = \{1,2,3,4,5,6,7\}$
For a team, $a \in A$ and number of cup wins $b \in B$ we can say that “$a$ is $R$-related to $b$” if team $a$ has won the cup $b$ times and denote this as $aRb$. The notation $aRb$ is actually just an abbreviation for writing $(a, b) \in R$.
We can list all the possible ordered pairs $(a, b)$ such that $a$ is related to $b$ by $R$ to form a finite set, i.e.
$R =${ (Marseilles, 1), (A C Milan, 3), (Ajax Amsterdam, 1), (Juventus, 1), (Borussia Dortmund, 1), (Real Madrid, 7), (Manchester United, 2), (Bayern Munich, 2), (Porto, 1), (Liverpool, 2), (Barcelona, 4), (Chelsea, 1), (Inter Milan, 1) }
It turns out that this set is actually a subset of a larger finite set that includes all possible “team / number of cups” pairings obtained by forming the Cartesian product, $A \times B$ , of the sets $A$ and $B$.
Before going on to discuss relations in more detail we need to remind ourselves of some definitions we previously met in the unit on sets.
1.2. Cartesian product
If $A$ and $B$ are two sets the Cartesian product of $A$ and $B$ is the set
$A \times B = \{(a, b) : a \in A \; \text{and} \; b \in B \}$.
which is read as “ $A$ cross $B$”.
Note that $A \times A$ is often written as $A^2$ .
Example 1
Let $A = \{a, b\}$ and $B = \{0, 1, 2\}$ then
$A \times B = \{(a, 0), (a, 1), (a, 2), (b, 0), (b, 1), (b, 2) \}$
and
$B \times A = \{(0, a), (0, b), (1, a), (1, b), (2, a), (2,b)\}$.
In general, $A \times B$ and $B \times A$ are different sets.
End of Example 11.3. Cardinality of a set
The cardinality of a finite set $A$, denoted $\mid A \mid$ , is the number of elements in $A$.
The cardinality of the Cartesian product of two finite sets $A$ and $B$ is
$\mid A \times B \mid \;\; = \mid A \mid \cdot \mid B \mid$.
Example 2
In Example 1, $ \mid A \mid = 2$ and $ \mid B \mid = 3$ so that the cardinality of the Cartesian cross product is
$\mid A \times B \mid \;\; = \mid A \mid \cdot \mid B \mid$
$= 2 \times 3 \;\;\; = 6$.
End of Example 2 -
2. Relations
A relation $R$ from a set $A$ to another set $B$ is a subset of the set $A \times B$.
Let $R$ be a relation from $A$ to $B$. Then $R$ is a set of ordered pairs $(a, b)$ where $a \in A, \; b \in B$ and exactly one of the following is true:
(a). if $(a, b) \in R$ then we say “$a$ is $R$-related to $b$” and write $aRb$ .
(b). if $(a, b) \notin R$ then we say that “$a$ is not $R$-related to $b$” and write $a \class{strike}{R}b$.
We note here that an alternative notation for $aRb$ is $a \sim b$.
Example 3
Let $A = \{u, v, w \}, \; B = \{3, 5, 7, 9\}$ and define a relation $R$ from $A$ to $B$ as
$R = \{(u, 5), (u, 9), (w, 5), (w, 7)\}$.
Note that $R$ is a relation from $A$ to $B$ and is a subset of $A \times B$ where,
$A \times B = \{(u,3), (u,5), (u,7), (u,9), (v,3), (v,5), (v,7), (v,9), (w,3), (w,5), (w,7), (w,9)\}$.
For the relation $R$ we have:
$uR5, \; uR9, \; wR5, \; wR7,$ but $u\class{strike}{R}3,\; u\class{strike}{R}7,\; v\class{strike}{R}3,\; v\class{strike}{R}5, \; v\class{strike}{R}7, \; v\class{strike}{R}9, \; w\class{strike}{R}3, \; w\class{strike}{R}9,$
End of Example 3Example 4
If $R$ is a relation from $A$ to $A$ we say that $R$ is a relation on $A$.
In this case $R$ is a subset of $A \times A = A^2$.
Let $A = \{2,3,5,7\}$ and consider the set
$R = \{(3, 2), (5, 3), (5, 2), (7, 2), (7, 3), (7, 5)\}$.
The set $R$ is a relation on $A$ since $R \subseteq A \times A$
Note that $R$ is actually the relation “is greater than” $( > )$ for the set $A$. For all ordered pairs $(a,b) \in R$ we have that $a > b$ .
End of Example 42.1. Domain and range of a relation
Let $R$ be a relation from $A$ to $B$. Two sets associated with the relation $R$ are the domain and range of $R$.
The domain is the set of all possible inputs the relation is defined for, i.e. the first component of the ordered pair. In set notation we have,
$dom(R) = \{a : (a,b) \in R$ for some $b \}$.
The range, on the other hand, is the set of all possible outputs the relation can generate from the input values, i.e. the second component of the ordered pair. In set notation,
$rng(R) = \{b : (a,b) \in R$ for some $a \}$.
Example 5
Let $A = \{1,3,4\}$ and $B = \{0,2,4,6\}$.
Define $R$ to be the “is less than” $( < )$ relation from $A$ to $B$.
Determine $R$ and write down the domain and range of $R$.
Solution
Write down the product set:
$A \times B = \{(1,0), (1,2), (1,4), (1,6), (3,0), (3,2), (3,4), (3,6), (4,0), (4,2), (4,4), (4,6)\}$
Identify which of the ordered pairs in $A \times B$ are in $R$.
$(1,0) \notin R$ since 1 is not less than 0.
$(1,2) \in R$ since 1 is less than 2.
$(1,4) \in R$ since 1 is less than 4.
$(1,6) \in R$ since 1 is less than 6.
$(3,0) \notin R$ since 3 is not less than 0.
$(3,2) \notin R$ since 3 is not less than 2.
$(3,4) \in R$ since 3 is less than 4.
$(3,6) \in R$ since 3 is less than 6.
$(4,0) \notin R$ since 4 is not less than 0.
$(4,2) \notin R$ since 4 is not less than 2.
$(4,4) \notin R$ since 4 is not less than 4.
$(4,6) \in R$ since 4 is less than 6.
Form the set $R$ of all ordered pairs where the first component is less than the second component, i.e.
$R = \{(1,2),(1,4),(1,6),(3,4),(3,6),(4,6)\}$
The domain of $R$ is the set of all first components of the ordered pairs in $R$.
The range of $R$ is the set of all second components of the ordered pairs in $R$.
In this case, $dom(R) = \{1,3,4\}$ and $rng(R) = \{2,4,6\}$.
End of Example 52.2. Difference between a relation and a function
Further resources can be found at:
🔗 Understanding Relations and Functions
Recall from the previous unit that functions are a special type of relation and a function $f$ can be represented as a set of ordered pairs, $(a, b)$ where the first component, $a$, is an element in the domain of $f$ and the second component, $b$, is an element in the range of $f$. By definition for each input to a function there is exactly one output. So, given a list of ordered pairs if a first component is repeated then we do not have a function.
Example 6
Let $A = \{a, b, c, d\}$ and $B = \{1, 2, 3, 4\}$
The relation $R$, from $A$ to $B$, represnted by the set
$R = \{(a,1), (b,3), (c,2), (d,4)\}$
is a function as no two elements have the same first component.
However, the relation $S$, from $A$ to $B$, given by
$S = \{(a,1), (b,3), (c,2), (a,4), (d,3)\}$.
is not a function, as elements $(a, 1)$ and $(a, 4)$ have the same a first component. It is however a relation.
We conclude that all functions are relations but not all relations are functions.
End of Example 6 -
3. Representing relations
As is the case for functions there are several ways in which a relation can be represented.
3.1. Arrow diagram representation
A relation between finite sets can be represented diagrammatically by a collection of arrows pointing from the domain to the range.
Example 7
Let $X = \{1,2,4,8\}$ and $Y = \{1, 3, 9\}$. Define a relation $R$ from $X$ to $Y$ as follows:
Given any $(x,y) \in X \times Y$.
$(x, y) \in R$ if and only if $x \ge y$.
(i). Write down the product set $X \times Y$ .
(ii). Determine the relation $R$ and identify its domain and range.
(iii). Sketch the arrow diagram of $R$.
Solution
(i). Construct the Cartesian product:
$X \times Y = \{(1,1),(1,3),(1,9),(2,1),(2,3),(2,9),(4,1),(4,3),(4,9),(8,1),(8,3),(8,9)\}$.
(ii). Form the set $R$ of all ordered pairs where the first component is greater than or equal to $( \geqslant )$ the second component, i.e.
$R = \{(1,1),(2,1),(4,1),(4,3),(8,1),(8,3)\}$.
Here $dom(R) = \{1,2,4,8\}$ and $rng(R) = \{1,3\}$.
(iii). Arrows are drawn from $a \in A$ to $b \in B$ when $a$ and $b$ are related.
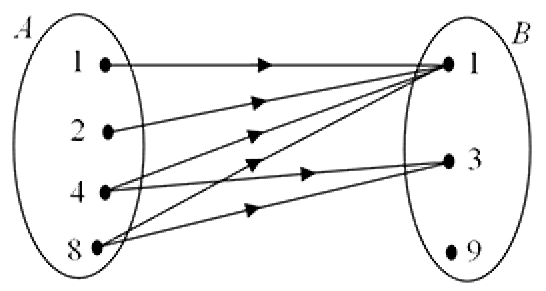
Note that $R$ is a relation but not a function as the elements $4$ and $8$ in $A$ both map to more than one element of $B$.
End of Example 73.2. Matrix representation
Matrices provide a highly efficient method for representing relations as they can effectively summarise information that may be difficult to extract from ordered pairs or arrow diagrams as set sizes increase. Furthermore, they have many advantages when it comes to analysing the properties of a relation.
Consider a relation $R$ from a set $A$ to a set $B$ where $\mid A \mid = n$ and $\mid B \mid = p$ .
We can represent $R$ by a matrix $M$, say, with $n$ rows and $p$ columns.
A $1$ or $0$ is placed in the matrix depending on whether or not elements of $A$ and $B$ are related. The $(i, j)-th$ entry of $M$ is a $1$ if $a_i \in A$ is related to $b_j\in B$, i.e.
$m_{ij} = \Bigg\{\matrix{1 \; \text{if}\; (a_i, b_j) \in R \\ 0 \; \text{if} \; (a_i, b_j) \notin R}$
Example 8
Referring to Example 7 we defined
$A = \{1,2,4,8\}$ and $B = \{1,3,9\}$
and found a relation $R (\ge)$ from $A$ to $B$ to be
$R = \{(1,1),(2,1),(4,1),(4,3),(8,1),(8,3)\}$.
In this case the matrix $M$ will have 4 rows, as $\mid A \mid = 4$, and 3 columns as, $\mid B \mid = 3$.
To identify the entries of $M$ we write the elements in $A$ to the left of the matrix and the elements in $B$ above the matrix as shown below. So, we index the rows of $M$ over the set $A$ and index its columns over the set $B$. Now check whether each pair, formed from the row/column pairings is in $R$. If such a pairing appears in $R$ then place a $1$ in the corresponding position in $M$ and a $0$ otherwise.
- Referring to the relation $R$ given above we start by completing the first row of $M$ by pairing the element $1$ with each of the column headings, $1$, $3$ and $9$ and checking whether the resulting pairs are in $R$.
- Element $(1,1)$ is in $R$ so place a $1$ in $M$ at the intersection of the row labelled $1$ and the column labelled $1$.
- Element $(1,3)$ is not in $R$ so place a $0$ in $M$ at the intersection of the row labelled $1$ and the column labelled $3$.
- Element $(1,9)$ is not in $R$ so place a $0$ in $M$ at the intersection of the row labelled $1$ and the column labelled $9$.
- Moving on to the second row:
- Element $(2,1)$ is in $R$ so place a $1$ in $M$ at the intersection of the row labelled $2$ and the column labelled $1$.
- Element $(2,3)$ is not in $R$ so place a $0$ in $M$ at the intersection of the row labelled $2$ and the column labelled $3$.
- Element $(2,9)$ is not in $R$ so place a $0$ in $M$ at the intersection of the row labelled $2$ and the column labelled $9$.
We continue in this manner for the remaining two rows to obtain the matrix given below,
$\matrix{1 \;\;\;\, 3 \;\;\;\, 9}$
$M = \matrix{1 \\ 2 \\ 4 \\ 8}\pmatrix{1 & 0 & 0 \\ 1 & 0 & 0 \\ 1 & 1 & 0 \\ 1 & 1 & 0}$.
End of Example 83.3. Directed graph representation
In a later unit we shall be looking at the concept of a graph as a mathematical structure, consisting of vertices (points) joined together by lines, as a method for representing relationships. In a directed graph, or digraph the direction of an edge is fixed and indicates the direction of the relationship. It is only permissible to move between two vertices in the specified direction.
Example 9
Given the set $A = \{1,2,3,4,5\}$ and the following relation $R$ on $A$,
$R = \{(1,2),(2,3),(2,4),(3,3),(3,4),(4,2),(4,5),(5,1)\}$.
Sketch the digraph associated with this relation.
Solution
The digraph will have $5$ vertices, one for each value in the set $A$. An element $(a, b)$ in $R$ indicates that there is a directed edge from $a$ to $b$. Checking the ordered pairs of $R$ in turn we have:
Element $(1,2)$ indicates there is an edge from vertex $1$ to vertex $2$.
Element $(2,3)$ indicates there is an edge from vertex $2$ to vertex $3$.
Element $(2,4)$ indicates there is an edge from vertex $2$ to vertex $4$.
Element $(3,3)$ indicates there is an edge from vertex $3$ to vertex $3$.
Element $(3,4)$ indicates there is an edge from vertex $3$ to vertex $4$.
Element $(4,2)$ indicates there is an edge from vertex $4$ to vertex $2$.
Element $(4,5)$ indicates there is an edge from vertex $4$ to vertex $5$.
Element $(5,1)$ indicates there is an edge from vertex $5$ to vertex $1$.
We can now sketch the digraph representing the relation $R$ as shown below.
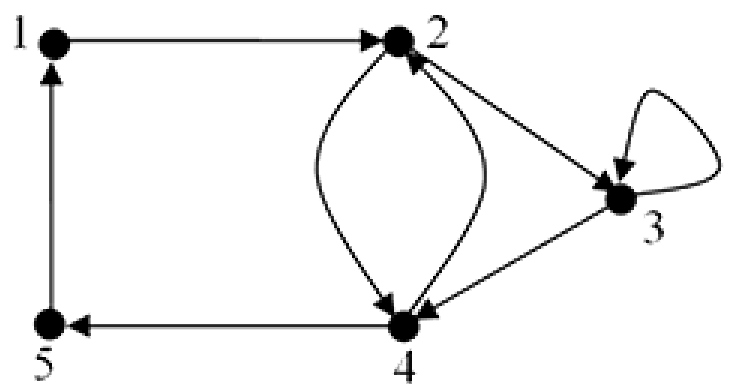
Note that the ordered pair $(3,3)$ is represented by a self-loop, i.e. an edge that connects vertex $3$ to itself.
End of Example 9 -
4. Inverse relation
Suppose $R$ is any relation from a set $A$ to a set $B$. The inverse relation, $R^{-1}$ , is defined as
$R^{-1} = \{(y,x) : (x,y) \in R \}$.
Note: These are the ordered pairs that when reversed belong to $R$, i.e. $(R^{-1})^{-1} = R$.
Example 10
If we define a relation
$R = \{(0,4),(4,6),(2,5),(1,7),(3,5)\} $
then
$R^{-1} = \{(4,0),(6,4),(5,2),(7,1),(5,3)\}$.
Notes:
The domain of $R$ is $\{0,1,2,3,4\}$ which is the range of $R^{-1}$.
The range of $R$ is $\{4,5,6,7\}$ which is the domain of $R^{-1}$.
Reversing the ordered pairs in $R^{-1}$ corresponds to calculating $(R^{-1})^{-1}$ and retrieves the original relation, $R$.
End of Example 10Example 11
Let $X = \{2,3,4\}$ and $Y = \{6,7,8\}$. Define a relation $S$ from $X$ to $Y$ as follows:
For all $(x,y) \in X \times Y$,
$(x,y)\in S$ if and only if $x \mid y$.
Note that “$\mid$” is the “divides” relation and we read $x \mid y$ as “ $x$ divides $y$”.
(i). Write down the relations $S$ and $S^{-1}$.
(ii). Describe $S^{-1}$ in words.
(iii). Write down the matrix representations for each of $S$ and $S^{-1}$.
Solution
(i). First write the set
$X \times Y = \{(2,6),(2,7),(2,8),(3,6),(3,7),(3,8),(4,6),(4,7),(4,8) \}$.
Checking the ordered pairs in $X \times Y$ we have
$2 \mid 6, \;\; 2 \mid 8, \;\; 3 \mid 6$ and $4 \mid 8$ so that
$S = \{(2,6),(2,8),(3,6),(4,8) \}$.
To obtain the elements in $S^{-1}$ we reverse the ordered pairs in $S$, i.e.
$S^{-1} = \{(6,2),(8,2),(6,3),(8,4) \}$.
(ii). For all $(y,x) \in Y \times X$.
$y\,S^{-1}x$ means that $y$ is a multiple of $x$.
(iii). The matrix representation for $S$ is
$\matrix{6 \;\;\;\, 7 \;\;\;\, 8}$
$M = \matrix{2 \\ 3 \\ 4 }\pmatrix{1 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 0 & 1 }$.
Here we note that, in general, if $M$ is the matrix corresponding to a relation $S$ then the matrix associated with the inverse relation $S^{-1}$ is obtained by transposing $M$. Hence, the matrix representation for $S^{-1}$ is
$\matrix{2 \;\;\; 3 \;\;\; 4}$
$M^T = \matrix{6 \\ 7 \\ 8 }\pmatrix{1 & 1 & 0 \\ 0 & 0 & 0 \\ 1 & 0 & 1 }$.
End of Example 11 -
5. Composition of relations
In the previous unit we described how to form the composition of two functions, an idea we now extend to compose two relations.
Let $A$, $B$ and $C$ be three sets and define $R$ to be a relation from $A$ to $B$ and $S$ to be a relation from $B$ to $C$.
The composition of $S \;o\; R$ is a relation from $A$ to $C$ and is defined as,
$S \; o \; R = \{(a,c) \in A \times C :$ there exists $b \in B$ for which $(a,b) \in R$ and $(b,c) \in S \}$
Here we think of $R$ as the first relation and $S$ as the second. Compare this with the composition of two functions in the previous unit where the notation $g \;o\; f$ indicated that we apply the function $f$ first followed by the function $g$.
Example 12
Let $A$, $B$ and $C$ be sets defined as
$A \{a,b,c,d\}, \; B = \{1,2,3,4\}$ and $C = \{u,v,w,x,y\}$.
Let $R$ be a relation from $A$ to $B$ and $S$ be a relation from $B$ to $C$ given by
$R = \{(a,1),(a,2),(b,3),(c,2),(d,3),(d,4) \}$
$S = \{(1,u),(1,v),(2,w),(3,v),(4,w),(4,x),(4,y) \}$.
Determine the composite relation $S \;o\; R$.
Solution
- Applying $R$ first and then $S$ gives,
- $R$ takes $a$ to $1$ and $S$ takes $1$ to $u$, so the composite relation takes $a$ to $u$.
- $R$ takes $a$ to $1$ and $S$ takes $1$ to $v$, so the composite relation takes $a$ to $v$.
- $R$ takes $a$ to $2$ and $S$ takes $2$ to $w$, so the composite relation takes $a$ to $w$.
- $R$ takes $b$ to $3$ and $S$ takes $3$ to $v$, so the composite relation takes $b$ to $v$.
- $R$ takes $c$ to $2$ and $S$ takes $2$ to $w$, so the composite relation takes $c$ to $w$.
- $R$ takes $d$ to $3$ and $S$ takes $3$ to $v$, so the composite relation takes $d$ to $v$.
- $R$ takes $d$ to $4$ and $S$ takes $4$ to $w$, so the composite relation takes $d$ to $w$.
- $R$ takes $d$ to $4$ and $S$ takes $4$ to $x$, so the composite relation takes $d$ to $x$.
- $R$ takes $d$ to $4$ and $S$ takes $4$ to $y$, so the composite relation takes $d$ to $y$.
We therefore have the following paths from $A$ to $C$.
$a \to 1 \to u, \;\;\; a \to 1 \to v, \;\;\; a \to 2 \to w$
$b \to 3 \to v, \;\;\; c \to 2 \to w, \;\;\; d \to 3 \to v,$
$d \to 4 \to w, \;\;\; d \to 4 \to x, \;\;\; d \to 4 \to y$.
The arrow diagram representation of the above is:
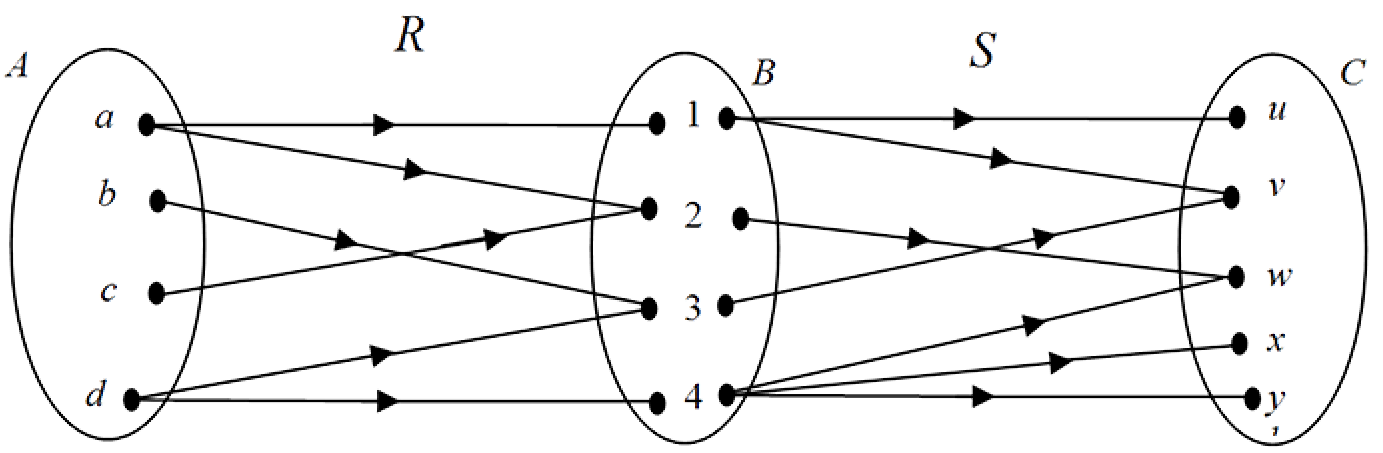
Hence, the composite relation is:
$S\; o\; R = \{(a,u),(a,v),(a,w),(b,v),(c,w),(d,v),(d,w),(d,x),(d,y)\}$
In arrow diagram format we have
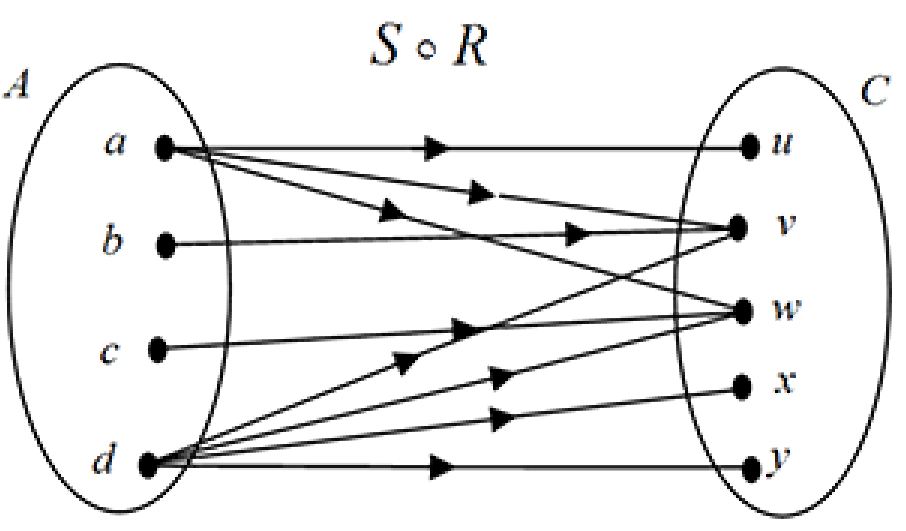
Note that some texts use the notation $R \;o\; S$ to represent the composition we have described above so you should be clear on the convention used. Although writing $R \;o\; S$ can lead to some confusion and goes against the notation we, and many authors, use for the composition of functions and relations it does have advantages when studying the connection between composition of relations and the associated products of their matrices. We do not consider this topic here.
End of Example 12 -
6. Types of Relation
Further resources can be found at:
Equivalence Relations Definition and Examples - (Watch up to 9:20)
There are various types of relations that can be defined on a set $A$ and the following paragraphs describe some of these relations.
(i). A relation, $R$ on a set $A$ is reflexive if $aRa$ for all $a \in A$. In other words a relation $R$ on a set $A$ is reflexive if it contains the pairs $(a, a)$ for all $a$ in $A$.
(ii). A relation $R$ on a set $A$ is symmetric if whenever $aRb$ then $bRa$, i.e. if whenever $(a,b) \in R$ then $(b,a) \in R$.
(iii). A relation $R$ on a set $A$ is transitive if whenever $aRb$ and $bRc$ then $aRc$, i.e. if $(a,b) \in R$ and $(b,c) \in R$ then $(a,c) \in R$.
Example 13
Given the set $A = \{1, 2, 3\}$ and the following relation $R$ on $A$,
$R = \{(1,1),(1,2),(2,1),(2,3),(3,3)\}$.
Determine whether $R$ is: (i). reflexive; (ii). symmetric; (iii). transitive.
(i). The set $A$ contains the three elements $1$, $2$ and $3$. If $R$ is reflexive then it must contain the three pairs $(1, 1), (2, 2)$ and $(3, 3)$. However, $R$ does not include $(2, 2)$ and is therefore not reflexive.
(ii). $R$ is not symmetric as it contains $(2, 3)$ but does not contain $(3, 2)$.
(iii). $R$ is not transitive as it contains $(1, 2)$ and $(2, 3)$ but does not contain $(1, 3)$.
End of Example 13Example 14
Given the set $A = \{a,b,c,d\}$ and the following relation $R$ on $A$,
$R = \{(a,a),(a,b),(a,d),(b,a),(b,b),(c,c),(d,a),(d,d) \}$.
Determine whether $R$ is: (i). reflexive; (ii). symmetric; (iii). transitive.
Solution
(i). $R$ is reflexive as it contains all the pairs $(a, a), (b, b), (c, c)$ and $(d, d)$. Every element in $A$ is related to itself.
(ii). $R$ is symmetric as it contains the pairs $(a, b)$ and $(b, a)$ and the pairs $(a, d)$ and $(d, a)$.
As an alternative test we can use the property that states:
If a relation $R$, is symmetric then we must have that $R = R^{-1}$ .
Exercise: Show that in this case $R = R^{-1}$ so that $R$ is symmetric.
(iii). $R$ is not transitive as it contains $(b, a)$ and $(a, d)$ but does not contain $(b, d)$.
End of Example 146.1. Classifying relations using matrices
It is relatively straightforward to determine if a relation on a set $A$ is symmetric, or reflexive, or transitive from the matrix representation.
Let $M$ be a matrix representing a relation $R$ on a set $A$, where $\mid A \mid = n$.
Note that $M$ will be a $n \times n$ (square) matrix. Can you explain why this is the case?
(i). A relation $R$ is reflexive if and only if the matrix $M$ has the property,
$m_{ii} = 1\; \text{for}\; i = 1, 2, \dots, n$.
In other words, all the diagonal entries, i.e. $m_{1,1}, m_{2,2}, \dots , m_{n,n}$ must equal $1$.
(ii). A relation $R$ is symmetric if and only if $M = M^T$ .
(iii). A relation $R$ is transitive if and only if whenever an entry $(i, j)$ in $M^2$ is non-zero then the corresponding entry $(i, j)$ in $M$ is also non-zero.
Example 15
Let $A = \{1,2,3\}$ and define a relation $R$ on $A$ as follows.
Given any $(a,b) \in A \times A$.
$(a,b) \in R$ if and only if $a \le b$.
(i). Write down the relation $R$ and its matrix representation, $M$.
(ii). Use the matrix $M$ to determine whether $R$ is reflexive or symmetric, or transitive.
Solution
(i). $A \times A = \{(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3)\}$
Examine the set $A \times A$ to determine $R$ giving,
$R = \{(1,1),(1,2),(1,3),(2,2),(2,3),(3,3)\}$.
Construct the matrix $M$ from the elements of $R$, using the method described earlier:
$\matrix{1 \;\;\; 2 \;\;\;\, 3}$
$M^T = \matrix{1 \\ 2 \\ 3 }\pmatrix{1 & 1 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & 1 }$.
(ii). (a) All the diagonal entries of $M$ equal $1$ and so $R$ is reflexive.
(b). The matrix is not symmetric, i.e. $M \neq M^T$ and so $R$ is not symmetric.
(c). To check transitivity we calculate,
$\matrix{1 \;\;\; 2 \;\;\;\, 3}$
$M^2 = \matrix{1 \\ 2 \\ 3 }\pmatrix{1 & 2 & 3 \\ 0 & 1 & 2 \\ 0 & 0 & 1 }$.
If we compare the matrices $M^2$ and $M$ we find that for each non-zero entry in $M^2$ the matrix $M$ has a non-zero entry in the corresponding position. Hence, $R$ is transitive.
End of Example 156.2. Classifying relations using directed graphs
Provided the graph is of a “reasonable” size we can determine whether a relation is symmetric, reflexive or transitive by inspection, although transitivity is a little harder to show.
Example 16
In Example 9 we defined the set $A = \{1, 2, 3, 4, 5\}$ and a relation $R$ on $A$ as,
$R = \{(1,2),(2,3),(2,4),(3,3),(3,4),(4,2),(4,5),(5,1)\}$.
The directed graph for this relation is shown below.
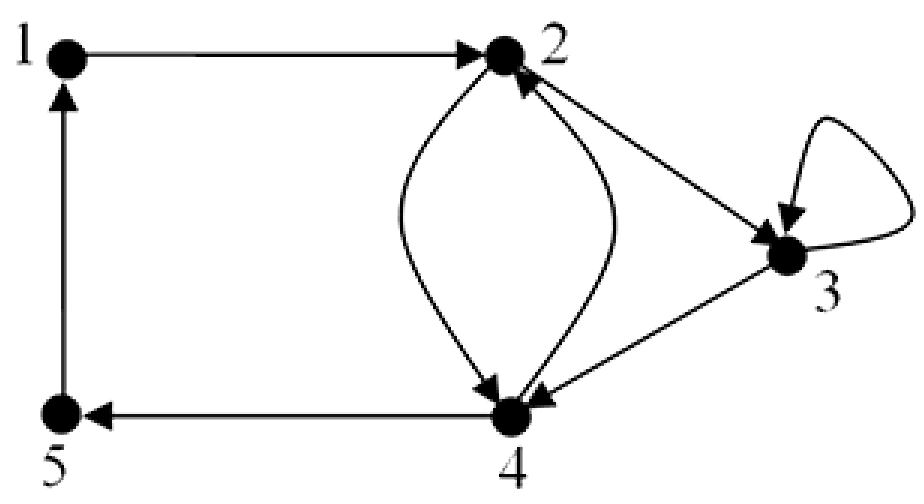
- Checking the three properties in turn:
- $R$ is reflexive if every vertex has a self-loop. Only vertex $3$ has a self-loop and so $R$ is not reflexive.
- $R$ is symmetric, if for every directed edge between two vertices we have another edge between these vertices pointing in the opposite direction. This condition is only satisfied for vertices $2$ and $4$ and so $R$ is not symmetric.
- $R$ is transitive if whenever there is an edge from a vertex to a second vertex and another edge from the second vertex to a third vertex then there is also an edge from the first to the third vertex. In other words, if we can get from a vertex to another vertex in two steps we must be able to make the same “journey” in one step.
Here $R$ is not transitive as for example, although we can move from vertex $1$ to vertex $2$ and then on to vertex $3$ we are unable to go directly from vertex $1$ to vertex $3$. Inspection of $R$ shows that while $(1, 2)$ and $(2, 3)$ are in $R$ it does not include $(1, 3)$.
End of Example 16X$\matrix{1 \;\;\; 2 \;\;\;\, 3}$
$M^2 = \matrix{1 \\ 2 \\ 3 }\pmatrix{1 & 1 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & 1 }$
-
7. Equivalence Relations
- A binary relation $R$ on a set $A$ is an equivalence relation if and only if:
- $R$ is reflexive, i.e. $(a,a) \in R$ for all $a$ in $A$.
- $R$ is symmetric, i.e. if whenever $(a,b) \in R$ then $(b,a) \in R$.
- $R$ is transitive, i.e. if $(a,b) \in R$ and $(b,c) \in R$ then $(a,c) \in R$.
Example 17
Define the set $A = \{1, 2, 3\}$ and the following relation $R$ on $A$,
$R = \{(1,1),(1,2),(2,1),(2,2),(3,3)\}$
Is $R$ an equivalence relation?
Solution
- We check the three properties, reflexive, symmetric and transitive.
- $R$ is reflexive as it contains all the pairs $(1, 1), (2, 2)$ and $(3, 3)$.
- $R$ is symmetric as it contains the pairs $(1, 2)$ and $(2, 1)$. Note that in this case these are the only two elements we need to check.
- $R$ is transitive as $(1, 2) \in R, (2, 1) \in R$ and $(1, 1) \in R$. Here this is all we need to check.
Hence, $R$ is an equivalence relation as it is reflexive, symmetric and transitive.
End of Example 17Example 18
Is the equality relation $(=)$ on the set of integers $( \mathbb{Z} )$ an equivalence relation?
Solution
- $x = x$ for all $x \in \mathbb{Z}$, hence $R$ is reflexive.
- If $x = y$ then $y = x$ for all $x,y \in \mathbb{Z}$, hence $R$ is symmetric.
- If $x = y$ and $y = z$ then $x = z$ for all $x,y,z \in \mathbb{Z}$, hence $R$ is transitive.
We have shown that $R$ is reflexive, symmetric and transitive and hence an equivalence relation.
End of Example 18Example 19
The relation $R$ defined as, “greater than or equal to”, $\ge$, on the set of integers $(\mathbb{Z})$ is not an equivalence relation.
- $x \ge x$ for all $x \in \mathbb{Z}$, since $x = x$. Hence $R$ is reflexive.
- if $x \ge y$ then it is not neccesarily true that $y \ge x$.
For example $3 \ge 1$ but $1 \ngeq 3$. Hence, $R$ is not symmetric. - If $x \ge y$ and $y \ge z$ then $x \ge z$ for all $x,y,z \in \mathbb{Z}$. Hence $R$ is transitive.
Although $R$ is both reflexive and transitive, it is not symmetric and therefore not an equivalence relation.
End of Example 19Example 20
A relation $R$ on the set of integers $( \mathbb{Z})$ is defined as follows:
$(x, y) \in R$ if and only if $x - y$ is divisible by $5$.
Show that $R$ is an equivalence relation.
Solution
- Let $x,y,z \in \mathbb{Z}$.
- $x - x = 0$ is divisible by $5$ for all $x$ in $\mathbb{Z}$ and so $(x, x) \in R$. Hence $R$ is reflexive.
- If $(x, y) \in R$ then $x - y$ is divisible by $5$. Since $y - x = - (x - y)$ then $y - x$ is divisible by $5$ and so $(y, x) \in R$. Hence $R$ is symmetric.
- If $(x, y) \in R$ and $(y, z) \in R$ then $x - y$ is divisible by $5$ and $y - z$ is divisible by $5$. Since $x - z = (x - y) + (y - z)$ then $x - z$ is divisible by $5$ and so $(x, z) \in R$. Hence, $R$ is transitive.
As $R$ is reflexive, symmetric and transitive it is an equivalence relation.
End of Example 20Example 21 (OPTIONAL)
Let $A$ be the set of fractions, i.e. $A = \Bigg\{{\Large\frac{p}{q}} : p, q \in \mathbb{Z},\; q \neq 0 \Bigg\}$.
Define a relation $R$ on $A$ by
${\Large\frac{a}{b}} R {\Large\frac{c}{d}}$ if and only if $ad = bc$
Show that $R$ is an equivalence relation.
Solution
- For any fraction ${\Large\frac{a}{b}}$ we have that ${\Large\frac{a}{b}} R {\Large\frac{a}{b}}$ since $ab = ba$. Hence, $R$ is reflexive.
- If ${\Large\frac{a}{b}} R {\Large\frac{c}{d}}$ then $ad = bc$, so $cb = da$ giving ${\Large\frac{c}{d}} R {\Large\frac{a}{b}}$. Hence, $R$ is symmetric.
- If ${\Large\frac{a}{b}} R {\Large\frac{c}{d}}$ and ${\Large\frac{c}{d}} R {\Large\frac{e}{f}}$ then $ad = bc$ and $c f = de$ .
We need to show that $\frac{a}{b} R \frac{e}{f}$.
Multiply the first equation by $f$ giving
$adf = bcf$ so
$adf = bde$ (since $cf = de$)
Divide through by $d \neq 0$ giving $af = be$ and so $\frac{a}{b} R \frac{e}{f}$ as required.
Hence, $R$ is transitive.
As $R$ is reflexive, symmetric and transitive it is an equivalence relation.
End of Example 21 -
8. Equivalence Classes
Let $A$ be a set and suppose $R$ is an equivalence relation on $A$. For any element $a$ in $A$ the set of elements of $A$ to which $a$ is related is called the equivalence class of $a$, and it is denoted by $[a]$. We therefore have
$[a] = \{b : (a,b) \in R \}$.
Example 22
Define the set $A = \{0, 1, 2, 3, 4, 5\}$ and the following equivalence relation $R$ on $A$,
$R = \{(0,0),(0,2),(0,4),(2,0),(2,2),(2,4),(4,0),(4,2),(4,4),(1,1),(1,3),(3,1),(3,3),(5,5) \}$
Determine the equivalence classes of $R$.
Solution
We need to find the equivalence class for each element, i.e. $0, 1, 2, 3, 4$ and $5$.
The equivalence class for $0$, denoted $[ 0 ]$, includes everything in $R$ that $0$ is related to. In other words, we select the second component of every ordered pair with $0$ as a first component.
Determining $[ 0 ]$ and all the other equivalence classes gives,
$[0] = \{0,2,4\}$
$[1] = \{1,3\}$
$[2] = \{0,2,4\}$
$[3] = \{1,3\}$
$[4] = \{0,2,4\}$
$[5] = \{5\}$$
Notes
(a). The union of the equivalence classes is the set $A$.
(b). The equivalence classes are either equal or disjoint.
(c). If two elements are related they have the same equivalence class. For example, $0, 2$ and $4$ are all related, as we can see from $R$, and they all have the same equivalence class, $[0] = [2] = [4] =\{0, 2, 4\}$ .
End of Example 22 -
9. Equivalence relations and partitions
In the unit on sets we defined a partition of a set $S$ to be a collection of non-empty subsets, $A_1, A_2, \dots, A_n$, that are mutually disjoint and their union equals the entire set $S$, i.e.
if $A_i \neq A_j$ then $A_i \cap A_j = \oslash$ and
$A_1 \cup A_2 \cup \dots \cup A_n = S$.
Example 23
The diagram shows a rectangular set $S$, partitioned into four mutually disjoint subsets whose union equals $S$.
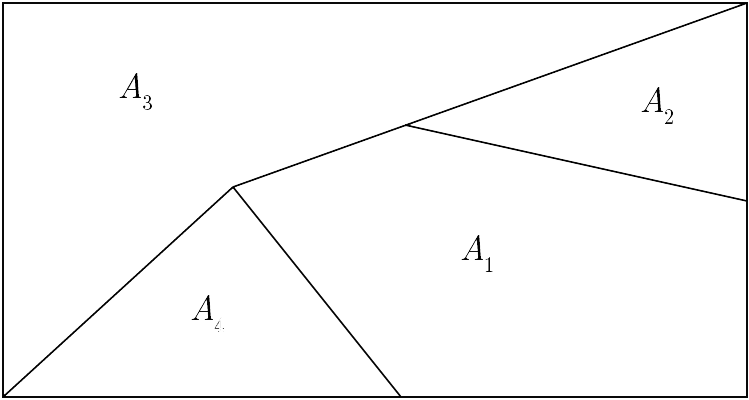 End of Example 23
End of Example 23In the following sections we briefly look at the connection between equivalence relations and partitions and show how:
(i). for an equivalence relation $R$ on a set $A$ the set of equivalence classes of $R$ forms a partition of $A$.
(ii). given a partition of a set $A$ there is an equivalence relation $R$ that has the subsets in the partition as its equivalence classes.
9.1. From equivalence relations to partitions
In Example 22 we found that the equivalence classes, associated with the equivalence relation $R$ on the set $A$, were either identical or disjoint and that their union was equal to $A$. So, given an equivalence relation on $A$ we are able to form a partition of $A$ from the equivalences classes as,
$\{\{0,2,4\}, \{1,3\}, \{5\}\}$
This result can be generalised to state that given any equivalence relation on a set $A$, the set of distinct equivalence classes associated with the relation forms a partition of $A$. We say that an equivalence relation on a set $A$ induces a partition of $A$.
Example 24
Let $A = \{1, 2, 3, 4\}$, and define a relation $R$ on the set $A$ as follows:
For all $(a,b) \in A \times A$.
$aRb$ if and only if $2 \mid (a + b)$.
(i). Write down the set $A \times A$.
(ii). Determine the relation $R$ and show that it is an equivalence relation.
(iii). Find the equivalences classes of $R$.
(iv). Write down the partition of the set $A$ induced by the relation, $R$.
Solution
(i). $A \times A = \{(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),$
$(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)\}$.
(ii). Identify which of the ordered pairs in $A \times A$ are in $R$.
$(1,1) \in R$ since $2 \mid (1 + 1)$
$(1,2) \notin R$ since $2 \not | \;(1 + 2)$
$(1,3) \in R$ since $2 \mid (1 + 3)$
$(1,4) \notin R$ since $2 \not | \; (1 + 4) \dots$
Continuing in this way we obtain
$R = \{(1,1),(1,3),(2,2),(2,4),(3,1),(3,3),(4,2),(4,4)\}$.
Exercise: Show that $R$ is reflexive, symmetric and transitive and hence an equivalence relation.
(iii). The equivalence class for $1$, denoted $[ 1 ]$, includes everything in $R$ that $1$ is related to. We therefore select the second component of every ordered pair that has $1$ as a first component. The other equivalence classes are found in a similar manner giving,
$[1] = \{1,3\}$ $[2] = \{2,4\}$.
$[3] = \{1,3\}$ $[4] = \{2,4\}$.
(iv). The partition of the set $A$ induced by the relation, $R$ is
$\{\{1,3\}, \{2,4\}\}$.
End of Example 249.2. From partitions to equivalence relations
We have seen how given an equivalence relation on a set we can form a partition of the set. In this section we show that it is possible to go the other way, and given a partition of a set construct an equivalence relation on the set. In order to do so we use the following theorem.
Theorem
For all $x,y \in A$
$xRy$ if and only if there exists a subset $A_i$ of the partition such that
both $x,y \in A_i$
Example 25
Define the set $X = \{3, 4, 5, 6, 7, 8, 9\}$ and consider the partition of $X$ given by,
$\{\{4,9\}, \{5,7\}, \{3,6,8\}\}$
Determine the relation $R$ induced by the partition.
Solution
Let $A_1 = \{4, 9\}, A_2 = \{5, 7\}$ and $A_3 = \{3, 6, 8\}$.
Here we use the above theorem which states that if two elements are in the same partition then they must be related. Considering the subset $A_1$ we have $4R4, 4R9, 9R4$ and $9R9$ giving the ordered pairs $(4, 4), (4, 9), (9, 4), (9, 9)$. We note here that these are the elements in the product set $A_1 \times A_1$.
Forming the Cartesian product of each subset with itself gives,
$A_1 \times A_1 = \{(4,4),(4,9),(9,4),(9,9)\}$
$A_2 \times A_2 = \{(5,5),(5,7),(7,5),(7,7) \}$
$A_3 \times A_3 = \{(3,3),(3,6),(3,8),(6,3),(6,6),(6,8),(8,3),(8,6),(8,8) \}$.
The equivalence relation $R$ is then obtained by forming the union of these three sets, i.e.
$R = \{ A_1 \times A_1 \cup A_2 \times A_2 \cup A_3 \times A_3 \}$
so that
$R = \{(4,4),(4,9),(9,4),(9,9),(5,5),(5,7),(7,5),(7,7),$
$(3,3),(3,6),(3,8),(6,3),(6,6),(6,8),(8,3),(8,6),(8,8) \}$.
Exercise: Show that $R$, induced from the given partition, is an equivalence relation.
End of Example 25 -
Summary
- In this unit we have introduced the concept of a binary relation on sets and you should now be able to:
- understand the difference between a relation and a function.
- understand the concepts of domain and range of a relation.
- determine a relation from a mathematical statement.
- represent relations as ordered pairs, arrow diagrams, matrices and directed graphs.
- determine the inverse of a relation.
- determine the composition of two relations.
- identify whether a relation is: reflexive, symmetric, transitive.
- understand the properties of an equivalence relation.
- identify whether a relation is an equivalence relation.
- determine equivalence classes for an equivalence relation.
- determine the partition of a set induced by an equivalence relation.
- determine an equivalence relation that induces a partition.
You should now attempt the tutorial exercises and Maple questions on GCU Learn
This is the final unit of the current block of study and the module will continue following the exam period.
Good luck with the class test!