-
1. Introduction
In this unit we provide a general introduction to number systems and discuss how numbers are represented by computers. We start with a look at the three main systems that occur in computing applications; decimal (base 10), binary (base 2) and hexadecimal (base 16) and describe methods for converting between these three bases. A (very) brief discussion is also presented on conversions involving other bases such as octal (base 8). We then apply the basic techniques we use to add and subtract decimal numbers to enable us to perform these operations manually for binary numbers. The discussion moves on to look at how computers store and represent positive and negative numbers and the concept of signed and unsigned binary numbers is introduced. We present different approaches used by computers for storing numbers with the focus on two’s complement representation. The unit closes with a brief look at a selection of bitwise operators, supported in programming languages such as Java and C, to operate on binary numbers at the bit-level by treating them as strings of bits.
-
2. Number systems
This section introduces the binary, decimal and hexadecimal number systems that correspond to the bases, 2, 10 and 16 respectively. A point to note here is that the number of digits used by a number system is equal to the base of the system.
2.1. Base 10 (Decimal)
We are all familiar with the decimal, or base-10, system for counting as we have been using it most of our lives. In the base-10 system all numbers are represented by combinations of the ten digits between 0 and 9. If we start counting from 0, in due course, we will reach the number 9 and, as we have no unused single digits left, we increment the “tens” digit by one to give the number “ten”, i.e. 10. Continuing to count we eventually reach 99 and, as we have no unused double digits left, we add one to the “hundreds” digit, giving 100.
Suppose for example, we continue to count until we reach the number 3472, say. We can tabulate this information as follows:
Place-Holder 103 102 101 100 Weight 1000 100 10 1 Decimal digit 3 4 7 2 In the decimal system the place-holder for each digit is a power of 10 so that moving from right to left, in the table, corresponds to an increase in magnitude by a factor of 10 at every step. To obtain the numerical value we multiply each decimal digit by its column’s weight and sum the values, i.e.
2 × 100 + 7 × 101 + 4 × 102 + 3 × 103 = 2 × 1 + 7 × 10 + 4 × 100 + 3 × 1000 = 2 + 70 + 400 + 3000 = 3472.
This number is therefore made up from the sum of: 2 “ones”, 7 “tens”, 4 “hundreds” and 3 “thousands”.
Sometimes decimal numbers are written with the subscript “10” to indicate a base 10 number, e.g. 347210.
2.2. Base 2 (Binary)
The binary, or base 2, number system uses the two digits 0 and 1 to represent numbers and is of particular importance in computing. In a computer’s memory elements can be in one of two states, OFF or ON corresponding to the digits 0 and 1 respectively. These elements represent one binary digit or bit. All internal processing and calculations in computing are done in binary. We have previously seen that in base 10 every number can be written as a weighted sum of powers of 10. In an analogous manner for base 2 we use a weighted sum of powers of 2 to express numbers. The place-holder for each digit is therefore a power of 2 and moving from right to left corresponds to an increase in magnitude by a factor of 2 at every step. For example, consider the following table.
Place-Holder 23 22 21 20 Weight 8 4 2 1 Decimal digit 1 1 0 1 The binary number in the table, 1101 can be written with the subscript “2” to indicate that it is a base 2 number, i.e. 11012 .
To obtain the decimal representation of 11012 we multiply each binary digit by its column’s weight and sum the values. Starting from the right,
1 × 20 + 0 × 21 + 1 × 22 + 1 × 23 = 1 + 0 + 4 + 8 = 13.
The number is therefore made up from the sum of 1 “ones”, 1 “fours” and 1 “eights”.
Hence, 11012 = 1310.
2.3. Base 16 (Hexadecimal)
The hexadecimal (often called hex) or base 16 number system uses sixteen symbols,
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F,
to represent numbers. The first ten digits are the same as in the decimal system while the remaining six, A to F, correspond to the numbers from 10 to 15 respectively.
A computer carries out all its operations in binary but as numbers become large the binary representation requires increasingly more digits (0’s and 1’s) and becomes difficult for humans to read and write. For this reason computers often display information, such as memory addresses, in hexadecimal as their format is more compact.
In base 16 we use a weighted sum of powers of 16 to express numbers. The place-holder for each digit is therefore a power of 16 and moving from right to left corresponds to an increase in magnitude by a factor of 16 at every step. Consider the table given below
Place-Holder 163 162 161 160 Weight 4096 256 16 1 Decimal digit 1 2 B F The hex number in the table, 12BF can be written with the subscript “16”, to indicate that it is a base 16 number, i.e. 12BF16.
To obtain the decimal representation of 12BF16 we multiply each hex digit by its column’s weight, noting that B represents 11 and F corresponds to 15, and sum the values, i.e.
15 × 160 + 11 × 161 + 2 × 162 + 1 × 163 = 15 + 176 + 512 + 4096 = 4799 .
Hence, 12BF16 = 479910.
2.4. Decimal to Binary to Hexadecimal Look-Up Table
The following table shows the decimal, 4-bit binary and hexadecimal representations of the numbers 0 to 15. You should familiarise yourself with these values.
Decimal
(Base 10)Binary
(Base 2)hexadecimal
(Base 16)0 0000 0 1 0001 1 2 0010 2 3 0011 3 4 0100 4 5 0101 5 6 0110 6 7 0111 7 8 1000 8 9 1001 9 10 1010 A 11 1011 B 12 1100 C 13 1101 D 14 1110 E 15 1111 F -
3. Converting Between Number Bases
In this section we look at converting integers between different number systems. While the main focus will be on the bases most commonly used in computing, i.e. 2 (binary), 10 (decimal) and 16 (hex) we also present some results for other bases including octal (base 8). The ability to convert back and forth between different bases is a fundamental skill required of anyone working in the area of computing.
A base number converter can be found here 🔗 http://www.kaagaard.dk/service/convert.htm
3.1. Converting from Base 10 to Any Base
Converting from base 10 (decimal) to any other base is easy. Start with the decimal number to be converted and repeatedly divide by the new base retaining the remainder at each step. We shall illustrate with some examples.
Example 1
(i). Base 10 (Decimal) to Base 2 (Binary)
Convert the decimal number 475 to a binary number.
Solution
Start by dividing 475 by 2 and keep the remainder. Repeat the process until we can no longer perform a division.
475 / 2 = 237, remainder 1
237 / 2 = 118, remainder 1
118 / 2 = 59, remainder 0
59 / 2 = 29, remainder 1
29 / 2 = 14, remainder 1
14 / 2 = 7, remainder 0
7 / 2 = 3, remainder 1
3 / 2 = 1, remainder 1
1 / 2 = 0, remainder 1
Now read the binary number from the bottom to the top: 111011011.
Hence, 47510 = 1110110112.
(ii). Base 10 (Decimal) to Base 16 (Hexadecimal)
Convert the decimal number 795 to a hex number.
Solution
Start by dividing 795 by 16 and keep the remainder. Repeat the process until we can no longer perform a division.
795 / 16 = 49, remainder 11 (= B in hex )
49 / 16 = 3, remainder 1
3 / 16 = 0, remainder 3
Now read the hex number from the bottom to the top: 31B.
Hence, 79510 = 31B16.
(iii). Base 10 (Decimal) to Base 8 (Octal)
Convert the decimal number 5361 to an octal number.
Solution
Start by dividing 5361 by 8 and keep the remainder. Repeat the process until we can no longer perform a division. The octal number system is similar to decimal except that it only uses the eight digits from 0 to 7.
5361 / 8 = 670, remainder 1
670 / 8 = 83, remainder 6
83 / 8 = 10, remainder 3
10 / 8 = 1,remainder 2
1 / 8 = 0, remainder 1
Now read the octal number from the bottom to the top: 12361. Hence, 536110 = 123618.
Note: Octal used to be popular when computers employed 12-bit, 24-bit or 36-bit words for data and addressing. However, as modern computers all use 16-bit, 32-bit or 64-bit words octal is rarely used nowadays.
(iv). Base 10 (Decimal) to Base 4 (Quaternary)
Convert the decimal number 679 to a base 4 number.
Start by dividing 679 by 4 and keep the remainder. Repeat the process until we can no longer perform a division.
679 / 4 = 169, remainder 3
169 / 4 = 42, remainder 1
42 / 4 = 10, remainder 2
10 / 4 = 2,remainder 2
2 / 4 = 0, remainder 2
Now read the base 4 number from the bottom to the top: 22213.
Hence, 67910 = 222134 .
(v). Base 10 (Decimal) to Base 5 (Quinary)
Convert the decimal number 5361 to a base 5 number.
Solution
Start by dividing 5361 by 5 and keep the remainder. Repeat the process until we can no longer perform a division.
5361 / 5 = 1072, remainder 1
1072 / 5 = 214, remainder 2
214 / 5 = 42, remainder 4
42 / 5 = 8,remainder 2
8 / 5 = 1, remainder 3
1 / 5 = 0, remainder 1
Now read the base 5 number from the bottom to the top: 132421.
Hence, 536110 = 1324215.
End of Example 13.2. Converting from Any Base to Base 10 (Decimal)
Converting to base 10 (decimal) from any other base is also fairly straightforward. We shall consider two methods.
Method 1 – Place Value Method
The first method is based on the “place values” of the digits in the number being converted.
Let $N_b = x_1\; x_2\; x_3 \dots x_m$ be a base $b$ number with $m$ digits.
To convert to base 10 we calculate as follows:
$N_{10} = x_{m}b^{0} + x_{m-1}b^{1} + x_{m-2}b^2 + \dots + x_1b^{m-1}$ [note the ordering!]
Method 2 – Shortcut Method
- Alternatively, we can apply the following algorithm which is much faster to use as numbers become larger.
- Start with the leftmost digit and multiply it by the base, $b$.
- Add the next digit and multiply by the base.
- Repeat until the rightmost digit has been added (Do not multiply by the base)
- This value is the result.
Example 2
(i). Binary to Decimal
(a). Convert the binary number 11001 to a decimal number.
Solution
Place-Value Method
The place values of digits in a binary number are powers of 2. To convert 11001 proceed as follows:
11001 = 1 × 20 + 0 × 21 + 0 × 22 + 1 × 23 + 1 × 24
= 1 + 0 + 0 + 8 + 16 = 25.
Hence, 110012 = 2510.
As base 2 only uses the numbers 0 and 1 this approach essentially involves adding the non-zero place values together.
Shortcut Method
- Alternatively, proceed as follows:
- Multiply the leftmost digit, 1, by the base, 2 giving 2.
- Write 2 in the middle row of the second column.
- Add, 1 + 2 = 3 and write 3 at the foot of the second column.
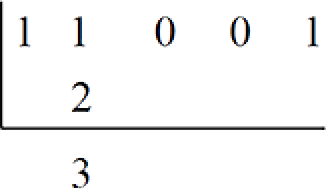
- Multiply 3 by the base, 2 to obtain 6.
- Write 6 in the middle row of the third column.
- Add, 0 + 6 = 6 and write 6 at the foot of the third column.
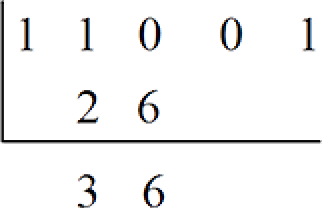
- Multiply 6 by the base, 2 to obtain 12.
- Write 12 in the middle row of the fourth column.
- Add, 0 + 12 = 12 and write 12 at the foot of the fourth column.
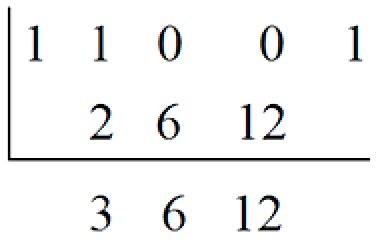
- Multiply 12 by the base, 2 to obtain 24.
- Write 24 in the middle row of the fifth column.
- Add the rightmost digit, 1 + 24 = 25 and write 25 at the foot of the fifth column.
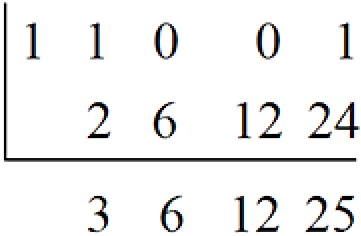
- The rightmost digit has been added and so we stop here.
Hence, 110012 = 2510 as obtained earlier.
(b). Convert the binary number 11011101 to a decimal number.
Solution
Place-Value Method
From the right, adding the place values, corresponding to the non-zero digits, in 11011101 gives:
1 + 0 + 4 + 8 + 16 + 0 + 64 + 128 = 221
Hence, 110111012 = 22110.
Shortcut Method
Alternatively, we can write
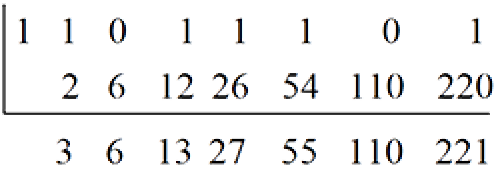
Hence, 110111012 = 22110
The shortcut method becomes more efficient the larger the binary number. It is also particularly useful as the base number increases in size and this is demonstrated in the following example.
(ii). Hexadecimal to Decimal
(a). Convert the hexadecimal number 3B2 to a decimal number.
Solution
Place-Value Method
The place values of digits in a hex number are powers of 16. To convert 3B2 to its decimal representation, starting from the right, multiply each digit in 3B2 by the appropriate power of 16.
3B216 = 2 × 160 + 11 × 161 + 3 × 162
= 2 × 1 + 11 × 16 + 3 × 256
= 2 + 176 + 768 = 946.
Hence, 3B216 = 94610.
Shortcut Method
Alternatively, we can use the shortcut method where we multiply by 16.

Hence, 32B16 = 94610.
(b). Convert the hexadecimal number 4BAE to a decimal number.
Solution
Place-Value Method
4BAE16 = 14 × 160 + 10 × 161 + 11 × 162 + 4 × 163
= 14 × 1 + 10 × 16 + 11 × 256 + 4 × 4096
= 19374.
Hence, 4BAE16 = 1937410.
Shortcut Method
Alternatively, calculate as follows:
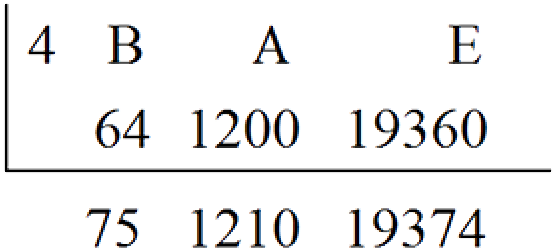
Hence, 4BAE16 = 1937410.
End of Example 2Example 3
We now apply the shortcut method to convert from bases, other than 2 and 16, to decimal.
(i). Octal to Decimal
Convert the octal number 7630 to a decimal number.
Solution
The place values of digits in an octal number are powers of 8 and so we need to multiply by 8 in our calculations.
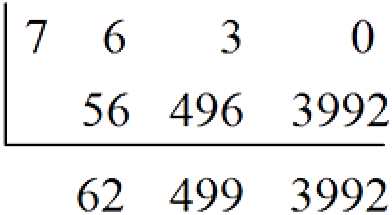
Hence, 76308 = 399210.
(ii). Base 5 to Decimal
Convert the base 5 number 4102 to a decimal number.
Solution
The place values of digits in an base 5 number are powers of 5 and so we need to multiply by 5 in our calculations.
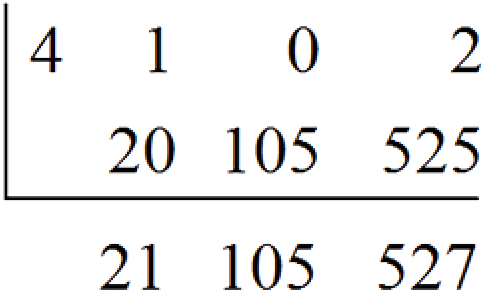
Hence, 41025 = 52710.
(iii). Base 7 to Decimal
Convert the base 7 number 21643 to a decimal number.
Solution
The place values of digits in a base 7 number are powers of 7 and so we need to multiply by 7 in our calculations.
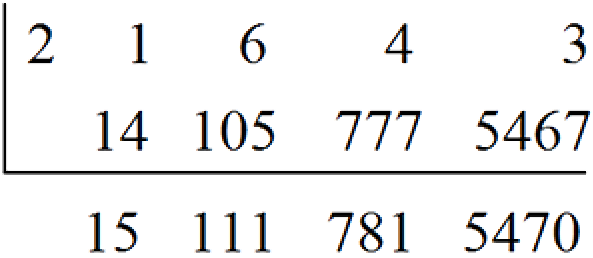
Hence, 216437 = 547010.
End of Example 33.3. Hexadecimal to Binary and Vice-Versa
3.3.1. Hexadecimal to Binary
As hexadecimal is base 16 = 24 and binary is base 2 = 21 every digit in a hex number can be replaced by its four bit binary equivalent.
Example 4
Convert the hexadecimal number 3C7D to a binary number.
Solution
Replace each hexadecimal number with its 4-bit binary equivalent.
Hex 3 C 7 D Binary 0011 1100 0111 1101 Hence, 3C7D16 = 00111100011111012.
End of Example 43.3.2. Binary to Hexadecimal
Example 5
Convert the binary number 1111110001001110 to a hexadecimal number.
Solution
- Starting from the right-hand side-split the number into groups of four. If necessary pad on the left with zeros to obtain a group of four.
- Convert each group of four to its decimal equivalent using the binary placeholder weightings, i.e. 1, 2, 4 and 8. For example, in the table below, the group of four on the right gives, 8 + 4 + 2 + 0 = 14. Hence, 11102 = 1410.
- Convert each decimal number to its hex equivalent, e.g. 1410 = E16.
Binary 1111 1100 0100 1110 Decimal 15 12 4 14 Hex F C 4 E Hence, 11111100010011102 = FC4E16.
Note: With a little practice you will be able to omit the ‘convert to decimal’ step and convert each group of four directly from binary to hex.
Now take this “hexadecimal quiz ”
🔗 Number Conversion Quiz: Hexadecimal To DecimalEnd of Example 53.4. Conversions Between Other Bases
Here we present some examples of how the methods described earlier can be applied to conversions between other bases.
Example 6
(i). Octal to Binary
As octal is base 8 = 23 and binary is base 2 = 21 every digit in an octal number can be replaced by its three bit binary equivalent.
Convert the octal number 761 to a binary number.
Solution
Replace each octal digit with its 3-bit binary equivalent.
Octal 7 6 1 Binary 111 110 001 Hence, 7618 = 1111100012.
(ii). Binary to Octal
Convert the binary number 1110101000101 to an octal number.
Solution
- Starting from the right hand side split the number into groups of three. If necessary pad on the left with zeros to obtain a group of three.
- Convert each group of three to its octal equivalent using the binary placeholder weightings, i.e. 1, 2 and 4. For example, on the right we have, 4 + 0 + 1 = 5. Hence, 1012 = 58.
Binary 001 110 101 000 101 Octal 1 6 5 0 5 Hence, 11101010001012 = 165058.
(iii). Hexadecimal to Octal
Convert the hexadecimal number 8B6E to an octal number.
Solution
One method is to convert the hex number to binary and then convert from binary to octal.
- Write each hex digit as a four bit binary number.
Hex 8 B 6 E Binary 1000 1011 0110 1110 - Starting from the right, split the binary representation into groups of three. Pad the leftmost triple with zeros if required.
Binary 001 000 101 101 101 110 Octal 1 0 5 5 5 6 Hence, 8B6E16 = 1055568.
(iv). Octal to Hexadecimal
Convert the octal number 6473 to a hex number.
Solution
All we have to do is reverse the process in the previous example.
- Write each octal digit as a three bit binary number.
Octal 6 4 7 3 Binary 110 100 111 011 - Starting from the right, split the binary representation into groups of four. Pad the leftmost group with zeros if required.
- Convert each binary number to its decimal equivalent, e.g. 10112 = 1110.
- Convert each decimal number to its hex equivalent, e.g. 1110 = B16.
Binary 1101 0011 1011 Decimal 13 3 11 Hex D 3 B Hence, 64738 = D3B16.
End of Example 6 -
4. Binary addition and subtraction
This section considers the operations of addition and subtraction of binary numbers. The methods described for addition are also (briefly) applied for hexidecimal numbers.
4.1. Binary addition
We first look at decimal addition to remind ourselves of the procedure.
Example 7
To evaluate 27 + 47 we write :
27
+ 47.- The rightmost column is the “ones column” and the column to its left is the “tens column”.
- Start with the “ones column” and perform the addition, 7 + 7 = 14.
- As 14 is greater than 9 we cannot write 14 in the “ones column”.
- The 1 is “carried” from the “ones column” and written at the top of the “tens column”.
- Write the 4 at the foot of the “ones column” :
1
27
+ 47
4 - Move to the “tens column” and calculate, 1 + 2 + 4 = 7.
- Write the 7 at the foot of the “tens column” :
27
+ 47
74
Hence, 27 + 47 = 74.
We now turn our attention to applying the techniques presented above to the addition of binary numbers.
- Binary addition is similar to decimal addition except that we only use the digits 0 and 1 as opposed to the digits from 0 to 9. In decimal addition a “carry” is generated when the sum is greater than 9 but in binary addition a “carry” is generated when the sum exceeds 1. We have
- 0 + 0 = 0 with no carry
- 0 + 1 = 1 with no carry
- 1 + 0 = 1 with no carry
- 1 + 1 = 0 and carry a 1 (recall that 10 in binary represents the decimal number 2).
End of Example 7Example 8
(i). Perform the same calculation as in Example 7 using the binary representations.
Solution
- Converting from decimal to binary: 2710 = 110112 and 4710 = 1011112 .
- Set up the addition:
0 1 1 0 1 1
+ 1 0 1 1 1 1 - Start at the right-hand-side in the “1’s column” .
- Adding, 1 + 1 = 10, ( 2 in decimal is 10 in binary ).
- Write down 0 and carry 1 into the “2’s column”:
1
0 1 1 0 1 1
+ 1 0 1 1 1 1
0 - In the “2’s column” we have, 1 + 1 + 1 = 11 , ( 3 in decimal is 11 in binary ).
- Write down 1 and carry 1 into the “4’s column”:
1 1
0 1 1 0 1 1
+ 1 0 1 1 1 1
1 0 - In the “4’s column” we have, 1 + 0 + 1 = 10.
- Write down 0 and carry 1 into the “8’s column”:
1 1 1
0 1 1 0 1 1
+ 1 0 1 1 1 1
0 1 0 - In the “8’s column” we have, 1 + 1 + 1 = 11 .
- Write down 1 and carry 1 into the “16’s column”:
1 1 1 1
0 1 1 0 1 1
+ 1 0 1 1 1 1
1 0 1 0 - In the "16's column" we have, 1 + 1 + 0 = 10
- Write down 0 and carry 1 into the “32’s column”:
1 1 1 1 1
0 1 1 0 1 1
+ 1 0 1 1 1 1
0 1 0 1 0 - In the “32’s column” we have, 1 + 0 + 1 = 10.
- Write down 10 and calculation is complete:
1 1 1 1 1
0 1 1 0 1 1
+ 1 0 1 1 1 1
1 0 0 1 0 1 0
It is straightforward to check the answer to obtain 10010102 = 7410 as in Example 7.
We can summarise the calculation above as follows:
Starting from the right:
Column 1 1 + 1 = 0, carry 1 into Column 2 Column 2 1 + 1 + 1, (carried) = 1, carry 1 into Column 3 Column 3 1 + 1 = 0, carry 1 into Column 4 Column 4 1 + 1 + 1 (carried) = 1, carry 1 into Column 5 Column 5 1 + 1 = 0, carry 1 into Column 6 Column 6 1 + 1 = 10 Reading the values in bold from bottom to top the solution is, 1001010 as obtained above.
(ii). Calculate the sum of the binary numbers, 11110 and 10111.
Solution
We proceed as in the previous example to obtain :
1 1 1
1 1 1 1 0
+ 1 0 1 1 1
1 1 0 1 0 1The answer can easily be checked by converting the two binary numbers to their decimal representations and adding, i.e. 30 + 23 = 53.
Compare this value with the decimal equivalent of our solution, i.e. 1101012 = 5310.
The two values agree and so our answer is correct.
Summarising the calculations above:
Starting from the right:
Column 1 0 + 1 = 1, no carry into Column 2 Column 2 1 + 1 = 0, carry 1 into Column 3 Column 3 1 + 1 + 1 (carried) = 1, carry 1 into Column 4 Column 4 1 + 1 = 0, carry 1 into Column 5 Column 5 1 + 1 + 1 (carried) = 11 Reading the values in bold from bottom to top the solution is, 110101 as obtained above.
End of Example 84.2. Binary subtraction
We first look at decimal subtraction to remind ourselves of the procedure.
Example 9
To evaluate 402 - 194 we write
402
-194
and proceed as follows.- Starting from the right-hand-side.
- The “1’s column” gives 2 - 4 which is negative and so we need to borrow one lot of 10 from the “10’s column”. Always borrow from the top line.
- We cannot borrow from the “10’s column” as the entry is 0.
- Borrow one lot of 100 from the “100’s column”. We now have three lots of 100 left.
- Split the borrowed 100 as, 100 = 9 × 10 + 10 × 1.
- Assign the nine lots of 10 to the “10’s column” and the one lot of 10 to the “1’s column”,
3 9 1
402
-194 - Start the subtraction process. In the “1’s column”, 12 - 4 = 8.
- Write the 8 in the “1’s column”,
3 9 1
402
-194
8 - In the “10’s column” we have, 9 - 9 = 0.
- Write the 0 in the “10’s column”,
3 9 1
402
-194
08 - In the “100’s column” we have, 3 - 1 = 2 .
- Write the 2 in the “100’s column”,
3 9 1
402
-194
208
Hence, the final answer is, 402 - 194 = 208.
End of Example 9We now apply these methods to the subtraction of binary numbers.
When it comes to binary subtraction the cases 0 - 0, 1 - 0 and 1 - 1 are easy.
Example 10
Evaluate 11102 - 10102.
Solution
Set up the subtraction:
1 1 1 0
- 1 0 1 0Starting from the right, the calculations are straightforward and can be summarised as follows:
Column 1 0 ‒ 0 = 0 Column 2 1 ‒ 1 = 0 Column 3 1 ‒ 0 = 1 Column 4 1 ‒ 1 = 0, Reading the values in bold from bottom to top the solution is, 0100 and we write:
1 1 1 0
- 1 0 1 0
0 1 0 0To check the answer, convert the original binary numbers to decimal giving, 14 - 10 = 4. The binary representation of the decimal number 4 is 0100 and so we have verified our answer.
End of Example 10The difficulty with binary subtraction is when we have the case 0 - 1. In this situation we must borrow from the columns to the left.
Example 11
Carry out the following binary subtraction, 10002 - 112.
Solution
Set up the subtraction:
$\;\;\;\;\,1 \;\; 0 \;\; 0 \;\; 0 \\ \underline{- \;\; 0 \;\; 0 \;\; 1 \;\; 1}$
- Start at the right-hand-side in the “1’s column”.
- The “1’s column” gives, 0 - 1 and we must borrow. (Always borrow from the top row).
- We cannot borrow from the “2’s column” as the top entry is 0.
- We cannot borrow from the “4’s column” as the top entry is 0.
- We can borrow from the “8’s column”.
- Write the borrowed 8 in the “4’s column” as two 4’s:
$\;\;\;\;\,0 \;\; \overset{1\\1}{0} \;\; 0 \;\; 0 \\ \underline{- \;\; 0 \;\; 0 \;\; 1 \;\; 1}$
- The top entry in the “8’s column” is now 0 as it has been moved to the “4’s column”.
- Borrow one of the 4’s from the fours column.
- Write the borrowed 4 in the “2’s column” as two 2’s:
$\;\;\;\;\; 0 \;\; \overset{1}{0} \;\; \overset{1\\1}{0} \;\; 0 \\\underline{- \;\; 0 \;\; 0 \;\; 1 \;\; 1}$
- Borrow one of the 2’s from the “2’s column”.
- Write the borrowed 2 in the “1’s column” as two 1’s:
$\;\;\;\;\; 0 \;\; \overset{\\1}{0} \;\; \overset{\\1}{0} \;\; \overset{1\\1}{0} \\\underline{- \;\; 0 \;\; 0 \;\; 1 \;\; 1}$
Starting from the right, the calculations are straightforward and can be summarised as follows:
Column 1 two 1’s subtract one 1 = 1 Column 2 1 ‒ 1 = 0 Column 3 1 ‒ 0 = 1 Column 4 0 ‒ 0 = 0, Reading the values in bold from bottom to top the solution is, 0101 and we write:
$\;\;\;\;\,1 \;\; 0 \;\; 0 \;\; 0 \\ \underline{- \;\; 0 \;\; 0 \;\; 1 \;\; 1}\\ \;\;\;\;\,0 \;\; 1 \;\; 0 \;\; 1$
Check the answer by converting to decimal:
1000 in binary is 8 in decimal and 11 in binary is 3 in decimal.
Then 8 - 3 = 5 and 5 in decimal is 0101 in binary as obtained above.
End of Example 11Example 12
Carry out the following binary subtraction, 11001011 - 10010010.
Solution
Starting from the right, the first four columns are easy:
$\;\;\;\;\; 1 \;\; 1 \;\; 0 \;\; 0 \;\; 1 \;\; 0 \;\; 1 \;\; 1 \\ \underline{- \;\; 1 \;\; 0 \;\; 0 \;\; 1 \;\; 0 \;\; 0 \;\; 1 \;\; 0} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; 1 \;\; 0 \;\; 0 \;\; 1$
- The “16’s column” gives, 0 - 1 and so we must borrow.
- We cannot borrow from the “32’s column” as its top entry is 0.
- We can borrow from the “64’s column” as its top entry is 1.
- Write the borrowed 64 in the “32’s column” as two 32’s.
- The top entry in the “64’s column” is now 0 as it has been moved to the “32’s column”.
$\;\;\;\;\; 1 \;\; 0 \;\; \overset{1\\1}{0} \;\; 0 \;\; 1 \;\; 0 \;\; 1 \;\; 1 \\ \underline{- \;\; 1 \;\; 0 \;\; 0 \;\; 1 \;\; 0 \;\; 0 \;\; 1 \;\; 0} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; 1 \;\; 0 \;\; 0 \;\; 1$
- Borrow one of the 32’s and write in the “16’s column” as two 16’s,
$\;\;\;\;\; 1 \;\; 0 \;\; \overset{ \\1}{0} \;\; \overset{1\\1}{0} \;\; 1 \;\; 0 \;\; 1 \;\; 1 \\ \underline{- \;\; 1 \;\; 0 \;\; 0 \;\; 1 \;\; 0 \;\; 0 \;\; 1 \;\; 0} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; 1 \;\; 0 \;\; 0 \;\; 1$
- Perform calculation,
$\;\;\;\;\; 1 \;\; 0 \;\; \overset{ \\1}{0} \;\; \overset{1 \\ 1}{0} \;\; 1 \;\; 0 \;\; 1 \;\; 1 \\ \underline{- \;\; 1 \;\; 0 \;\; 0 \;\; 1 \;\; 0 \;\; 0 \;\; 1 \;\; 0} \\ \;\;\;\;\; 0 \;\; 0 \;\; 1 \;\; 1 \;\; 1 \;\; 0 \;\; 0 \;\; 1$
Check:
11001011 in binary is 203 in decimal.
10010010 in binary is 146 in decimal.
Hence, 11001011 - 10010010 in binary is equivalent to 203 - 146 = 57 in decimal.
Also, 57 in binary is 111001 which confirms our answer.
A binary calculator is available here 🔗 Binary Calculator
Now attempt the exercises at this link. 🔗 Adding and Subtracting Binary Numbers
Do NOT use the calculator other than to check your answers.
End of Example 12 -
5. Addition and subtraction in other bases (OPTIONAL)
We can calculate the sum and difference of integers in other bases using methods similar to those described for decimal and binary calculations. The following examples illustrate the procedure for hexidecimal.
Example 13
Calculate the sum of the hex numbers, ABC and 2E3.
Solution
Set up the addition:
A B C
+ 2 E 3- Starting from the right:
- Column 1: (C + 3)16 = (12 + 3)10 = 1510 = F16 (no carry into Column 2)
- Write the F at the foot of Column 1:
A B C
+ 2 E 3
F - Column 2: (B + E)16 = (11 + 14)10 = 2510 = 1916 ( carry 1 into Column 3 )
- Write 9 at the foot of Column 2 and 1 at the top of Column 3:
1
A B C
+ 2 E 3
9 F - Column 3: (1 + A + 2)16 = (1 + 10 + 2)10 = 1310 = D16
- Write D at the foot of Column 2:
1
A B C
+ 2 E 3
D 9 F - Hence, ABC16 + 2E316 = D9F16.
An alternative approach is to convert ABC and 2E3 to their binary representations, perform the addition and then convert back to hex.
Replace each hexadecimal number with its binary equivalent.
Hex A B C Binary 1010 1011 1100 Hex 2 E 3 Binary 0010 1110 0011 We perform the addition:
1 0 1 0 1 0 1 1 1 1 0 0
+ 0 0 1 0 1 1 1 0 0 0 1 1
1 1 0 1 1 0 0 1 1 1 1 1Now convert from binary to hex.
Binary 1101 1001 1111 Decimal 13 9 15 Hex D 9 F Hence, ABC16 + 2E316 = D9F16 as obtained above.
The subtraction of hex numbers can also be performed using the methods described earlier.
End of Example 13Example 14
Calculate the following hexadecimal subtraction, ABC16 - 2E316.
Solution
The hex numbers were converted to binary in Example 13 and so we proceed as follows.
- Set up the subtraction
1 0 1 0 1 0 1 1 1 1 0 0
- 0 0 1 0 1 1 1 0 0 0 1 1
0 1 1 1 1 1 0 1 1 0 0 1
You should check the binary subtraction.
Now convert from binary to hex.
Binary 0111 1101 1001 Decimal 7 13 9 Hex 7 D 9 Hence, ABC16 - 2E316 = 7D916.
Exercise
Repeat the calculation in Example 14 by evaluating directly, i.e. do not convert to binary.
End of Example 14 -
Summary
- This unit has introduced number systems used in computing and you should now be able to:
- convert between different number bases, in particular binary, decimal and hexidecimal.
- add and subtract binary numbers.
You should now attempt the tutorial exercises on GCU Learn.
The next unit looks at how negative numbers are represented by computers and how calculations involving negative numbers are performed.