-
6. Representation of integers in computers
In the previous section we saw how to add and subtract binary numbers provided the numbers and the corresponding results are non-negative. We now look at how negative numbers are represented by computers and how calculations involving negative numbers are performed.
Watch: 📹 Representing Integers
6.1. Unsigned integers
Computers use a fixed number of binary digits (bits) to represent integers and they store data in registers. Registers come in different sizes and, depending on the processor, can be 8-bit, 16-bit, 32-bit or 64-bit. A 32-bit register, for example, can store 232 different values. An important point to note is that bits can only take the values 0 and 1, so that without some special method to account for negative integers only positive values and zero can be represented.
In computing the representation of integers can take one of two forms, signed or unsigned. The calculations in the previous section were all based on unsigned integers where a number with n bits could represent integers in the range 0 to 2n -1 . For example,
- 4 bits can represent the integers 0 to 15 (24 - 1)
- 8 bits can represent the integers 0 to 255 (28 - 1)
- 16 bits can represent the integers 0 to 65 535 (216 - 1), and so on.
To enable computers to represent negative numbers and perform arithmetic calculations such as subtraction, in terms of addition, we need to introduce the concept of signed integers.
6.2. Signed integers
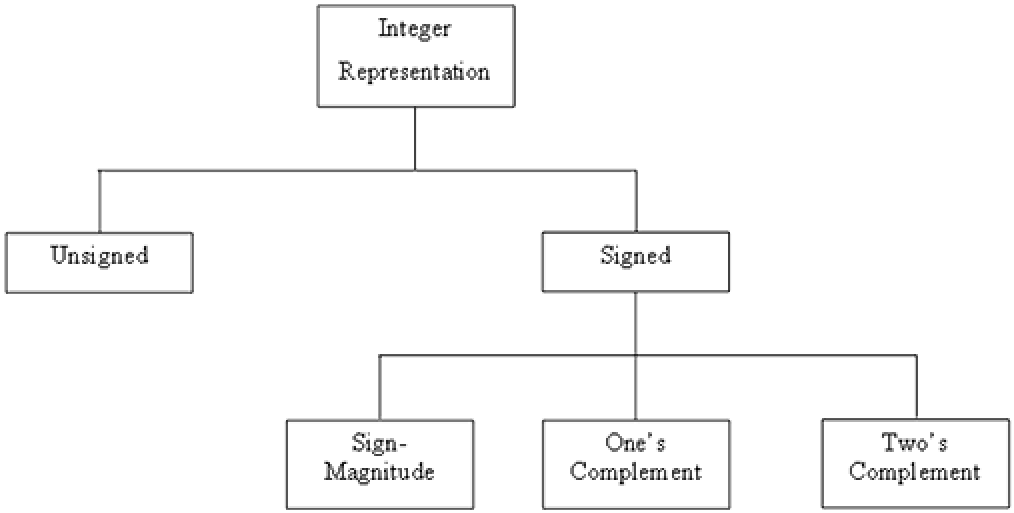
Unlike writing numbers on paper where we indicate a negative number by writing a minus sign in front of it a computer is unable to do this. There are several different methods that have been used to represent negative integers on a computer. Three such representations including: sign-magnitude, one’s complement and two’s complement are described here. In all three methods the leftmost bit, also called the most significant bit (MSB), is reserved as the “sign bit” with a 0 indicating a positive number and a 1 a negative number. The diagram below provides a schematic of methods of integer representation on a computer.
For simplicity we shall use a bit length of 8 but the results generalise to other bit lengths.
📹 One's Complement, Two's Complement, and Signed Magnitude
6.2.1. Sign-magnitude representation
The MSB (leftmost bit) gives the sign of the number and the remaining bits record its magnitude. A number with n bits can represent integers in the range, - 2n -1 + 1 to 2n -1 - 1. For example, with 8 bits the values, -127 to 127 are possible.
Example 15
The 8-bit sign-magnitude representation of 13 is:
+ / - 64 32 16 8 4 2 1 0 0 0 0 1 1 0 1 The 0 in the leftmost position indicates a positive number and we define its magnitude using the remaining 7 bits, i.e. 8 + 4 + 1 = 13.
The 8-bit sign-magnitude representation of -13 is:
+ / - 64 32 16 8 4 2 1 1 0 0 0 1 1 0 1 The 1 in the leftmost position indicates a negative number and we evaluate its magnitude using the remaining 7 bits as, 8 + 4 + 1 = -13.
Note that the representations for 13 and -13 only differ in the MSB.
- Although it is easy to implement, the method has several disadvantages including:
- Two representations for zero. For example, when working with 8 bits we have the problem of a “plus zero” 00000000 ( = + 010 ) and a “minus zero” 10000000 ( = - 010 ).
- Computationally inefficient.
The sign-magnitude representation is no longer used in computing.
📹 Binary Arithmetic 2: Sign Magnitude Representation
End of Example 156.2.2. One’s complement representation
In one’s complement the MSB again records the sign of the number and the remaining bits its magnitude. Using one’s complement a number with n bits can represent integers in the range, - 2n -1 + 1 to 2n - 1 - 1. Hence, with 8 bits the values, -127 to 127 are possible.
Example 16
Positive numbers are defined in the same manner as for sign-magnitude notation and so the 8-bit one’s complement representation of 13 is:
+ / - 64 32 16 8 4 2 1 0 0 0 0 1 1 0 1 To negate a number we take the one’s complement which involves “inverting” (“flipping”) all the bits, including the sign bit. In other words, we change 0’s to 1’s and 1’s to 0’s.
If we invert all the bits in the above, the one’s complement binary representation of -13 is:
+ / - 64 32 16 8 4 2 1 1 1 1 1 0 0 1 0 - The main disadvantages of one’s complement are:
- Two representations for zero. In the case of 8-bits these are, 00000000 and 11111111.
- Although an improvement on sign-magnitude there are still issues with some arithmetic operations.
One’s complement is no longer used but we do require knowledge of the technique when we come to discuss two’s complement.
End of Example 166.2.3. Two’s complement representation
As with the previous two methods the MSB records the sign and the remaining bits the magnitude of the number. Nowadays two’s complement is the most important, and widely used, method for representing integers in computing. Positive numbers are treated in exactly the same manner as for the previous methods, i.e. we simply write down the usual binary representation.
- To negate a number we perform the following steps:
- Write the binary representation of the number (as before).
- Invert all the bits (as in one’s complement).
- Add 1 to the result.
Example 17
The 8-bit two’s complement binary representation of 13 is:
+ / - 64 32 16 8 4 2 1 0 0 0 0 1 1 0 1 - To obtain the 8-bit two’s complement binary representation of - 13 proceed as follows:
- Write 13 in 8-bit binary: 00001101
- Invert the bits: 11110010
- Add 1: 11110011.
The 8-bit two’s complement of - 13 is therefore:
+ / - 64 32 16 8 4 2 1 1 1 1 1 0 0 1 1 Note that in two’s complement, unlike the two previous methods, there is only one representation for zero.
End of Example 17Example 18
Calculate the 8-bit two’s complement representation of zero.
Solution
- Write zero in 8-bit binary: 00000000
- Invert the bits: 11111111
- Add 1: 00000000.
Hence, the two’s complement of zero is zero.
Two’s complement provides an efficient method for storing and manipulating negative numbers. However, as with all signed approaches, where the MSB is reserved for the sign of the number, the range of numbers that the computer can store with two’s complement is reduced.
In general, for a number with n bits the range of two’s complement integers is from - 2n -1 to 2n - 1 - 1. For example, with 8 bits we can store the numbers between -12810 ( 100000002 ) to 12710 ( 011111112 ) inclusive.
End of Example 18Alternative definition of two’s complement
An alternative method for calculating the n-bit two’s complement of an integer $- a$, where $a > 0$, is defined to be the binary representation of 2n $- a$ .
Example 19
Calculate the 8-bit two’s complement binary representation for the following integers using the definition given above.
(i). 73 (ii). - 73 (iii). - 123
Solution
(i). As 73 is positive we simply write down the 8-bit binary representation, i.e. 7310 = 010010012.
(ii). Using the formula with n = 8 and a = 73 we have 28 - 73 = 256 - 73 = 183 = 10110111. Hence, -7310 = 101101112.
(iii). Using the formula with n = 8 and a = 123 we have 28 - 123 = 256 - 123 = 133 = 10000101 . Hence, - 12310 = 100001012.
Exercise: Check the results obtained above using the method described in Example 17.
End of Example 19📹 Binary 09: 8 bit 2's complement notation, alternative method
The table below shows the 4-bit representation of the integers between -7 and 8 in sign-magnitude, one’s complement and two’s complement format. Note that -8 only has a 4-bit representation in two’s complement.
Decimal Sign-Magnitude One's Complement Two's Complement -8 1000 -7 1111 1000 1001 -6 1110 1001 1010 -5 1101 1010 1011 -4 1100 1011 1100 -3 1011 1100 1101 -2 1010 1101 1110 -1 1001 1110 1111 0 0000 or 1000 0000 or 1111 0000 1 0001 0001 0001 2 0010 0010 0010 3 0011 0011 0011 4 0100 0100 0100 5 0101 0101 0101 6 0110 0110 0110 7 0111 0111 0111 📹 One's Complement, Two's Complement, and Signed Magnitude
Go here 📹 https://www.exploringbinary.com/twos-complement-converter/ for a Decimal/Two’s Complement Converter.
6.2.4. Converting decimals to 8-bit two’s complement
The first step is to convert the magnitude of the decimal number to binary in the usual way and pad with zeros to 8-bits if required. If the number is positive then we are done. Otherwise, we negate the binary number by inverting the bits (giving the one’s complement) and add 1 to obtain the two’s complement.
Example 20
(i). Convert -27 to an 8-bit two’s complement binary number.
(ii). Convert the decimal number 117 to an 8-bit two’s complement binary number.
Solution
- (i). Following the steps described earlier:
- 2710 = 000110112
- Invert the bits: 11100100 ( one’s complement )
- Add 1: 11100101.
Hence, the two’s complement of -2710 is 111001012 .
(ii). As this is a positive number all we have to do is to convert 117 directly to binary and pad, on the left, with zeros.
The two’s complement of 11710 is 011101012.
End of Example 206.2.5. Converting 8-bit two’s complement to decimal
Check the MSB to determine if the number is positive or negative.
If the MSB is a 0 the number is positive and we convert to decimal in the usual way.
- If the MSB is a 1, the number is negative and we convert to decimal as follows:
- Invert the bits.
- Add 1.
- Convert to a decimal.
- Negate the decimal to obtain the value of the original binary number.
Example 21
(i). Convert the 8-bit two’s complement binary number 011101002 to decimal.
(ii). Convert the 8-bit two’s complement binary number 110101012 to decimal.
Solution
(i). The leading number is a 0 and so this is a positive number. We therefore convert directly from binary to decimal, i.e. 011101002 = 11610.
- (ii). The leading 1 indicates that this is a negative number. Convert as follows:
- Number: 11010101
- Invert the bits: 00101010
- Add 1: 00101011
- Convert to decimal: 001010112 = 4310.
- Negate: 110101012 = -4310.
End of Example 216.2.6. 8 bit two’s complement binary addition
In the following we provide some examples of two’s complement binary addition. Recall that with 8 bits we can represent numbers between -128 and 127.
Example 22
(i). Adding two positive numbers between 0 and 127 whose sum is less than 127.
Calculate 19 + 104 using 8-bit two’s complement binary addition.
Solution
Both numbers are positive and so the 8-bit two’s complement of each number is simply the usual binary representation of each. We have
0 0 0 1 0 0 1 1
+ 0 1 1 0 1 0 0 0
0 1 1 1 1 0 1 1Check the answer: 011110112 = 12310 as expected.
(ii). Adding positive and negative integers in the range -128 to 127 where the positive integer has a greater magnitude. The sum lies in the range -128 to 127.
Calculate 94 + ( -41 ) using 8-bit two’s complement binary addition.
Solution
Two’s complement: 9410 = 010111102
- Determine two’s complement of -41:
- 4110 = 001010012
- Invert the bits: 11010110
- Add 1 to the above: 11010111
Then 94 + ( -41 ) is represented by,
0 1 0 1 1 1 1 0
+ 1 1 0 1 0 1 1 1
1 0 0 1 1 0 1 0 1Discard the leading 1 to give, 00110101.
Check the answer: 001101012 = 5310 as expected.
(iii). Adding positive and negative integers in the range -128 to 127 where the negative integer has a greater magnitude. The sum lies in the range -128 to 127.
Calculate 37 + ( -79 ) using 8-bit two’s complement binary addition.
Solution
Two’s complement: 3710 = 001001012
- Determine two’s complement of -79
- 7910 = 010011112
- Invert the bits: 10110000
- Add 1: 10110001.
Calculate 37 + ( -79 ) using,
0 0 1 0 0 1 0 1
+ 1 0 1 1 0 0 0 1
1 1 0 1 0 1 1 0The leading digit is a 1 and so this is negative binary number.
- Check: Convert from two’s complement binary to decimal.
- Number: 11010110
- Invert the bits: 00101001
- Add 1: 00101010.
- Convert to decimal: 001010102 = 4210.
- Negate: 110101102 = - 42 as expected.
(iv). Adding two negative integers in the range -128 to -1 when the sum also lies in the range, -128 to -1.
Calculate -41 + ( -52 ) using 8-bit two’s complement binary addition.
Solution
From earlier the two’s complement of -4110 = 110101112.
- Two’s complement of -52
- 5210 = 001101002
- Invert the bits: 11001011
- Add 1: 11001100.
Hence, -5210 = 110011002
Calculate -41 + ( -52 ) using,
1 1 0 1 0 1 1 1
+ 1 1 0 0 1 1 0 0
1 1 0 1 0 0 0 1 1Discard the leading 1 to give, 10100011.
The leading digit is a 1 and so this is a negative binary number.
- Check: Convert from two’s complement binary to decimal.
- Number: 10100011
- Invert the bits: 01011100
- Add 1: 01011101
- Convert to decimal: 010111012 = 9310.
- Negate: 101000112 = -9310 as expected.
End of Example 226.2.7. Two’s complement overflow
Using 8-bit two’s complement we can add two integers in the range, -128 to 127 provided their sum is also in this range. If values outside the range are encountered we obtain an error referred to as an overflow.
In two’s complement overflow is associated with obtaining the wrong sign in the answer when adding two numbers.
- We either
- obtain a negative result when adding two positive integers, or
- obtain a positive result when adding two negative integers.
Overflow cannot occur when adding numbers of opposite signs that are within the range.
Example 23
(i). Calculate 63 + 70 using 8-bit two’s complement binary addition.
Two’s complement: 6310 = 001111112
Two’s complement: 7010 = 010001102
Calculating 63 + 70 gives,
0 0 1 1 1 1 1 1
+ 0 1 0 0 0 1 1 0
1 0 0 0 0 1 0 1There is clearly something wrong here as the leading digit in the answer is a 1 which indicates a negative number! This is not possible as we added two positive integers, i.e. 63 and 70.
The problem is that the true answer in decimal form is 133 and this is outside the allowed range, i.e. 133 > 127.
End of Example 23Example 24
(i). Calculate -11 + ( -120 ) using 8-bit two’s complement binary addition.
- Two’s complement of -11:
- Number: 1110 = 000010112
- Invert the bits: 11110100
- Add 1: 11110101.
- Two’s complement of -120:
- Number: 12010 = 011110002
- Invert the bits: 10000111
- Add 1 to the above: 10001000.
Calculating -11 + ( -120 ) gives,
1 1 1 1 0 1 0 1
+ 1 0 0 0 1 0 0 0
1 0 1 1 1 1 1 0 1Discard the leading 1 leaving, 01111101.
There is clearly something wrong here as the leading digit in the answer is a 0 which indicates a positive number! This is not possible as we added two negative integers, i.e. -11 and -120.
The problem is that the true answer in decimal form is -131 and this is outside the allowed range, i.e. -131 < -128 .
End of Example 24 -
7. Bitwise logical operations
- Every computer represents numbers, and almost all data forms, with bits which are a series of $0$’s and $1$’s. Bitwise operators, as the name suggests, operate at a bit-level performing bit-by-bit operations. A number of bitwise operators are defined in Java and C programming including:
- The bitwise $\sim$ (tilde) operator performs a bitwise NOT operation.
- The bitwise $\&$ (ampersand) operator performs a bitwise AND operation.
- The bitwise $\mid$ (pipe) operator performs a bitwise OR operation.
- The bitwise $\hat{}$ (hat) operator performs a bitwise XOR operation.
The NOT, AND, OR and XOR are respectively analogous to the “not”, “and”, “or” and “exclusive-or” operations we met in propositional logic. Similarly, we can think of the “$1$” and “$0$” as corresponding respectively to the “T” and “F” in logic .
The following example demonstrates an application of each of the above operators.
Example 25
Suppose we have $x$ = 70 and $y$ = 23.
The binary representations are $x$ = 01000110 and $y$ = 00010111.
(i). The bitwise not operator is a unary operator (only one operand) and converts a 0 to a 1 and vice-versa.
Hence, $\sim x$ = 10111001 and $\sim y$ = 11101000.
Note: The bitwise not is also known as the one’s complement operator.
(ii). A bitwise AND applied to a pair of bits returns a 1 if both bits are 1, and a 0 otherwise.
Hence, $x\, \& \,y$ = 00000110.
(iii). A bitwise OR applied to a pair of bits returns a 1 if at least one of the bits is a 1, and a 0 otherwise.
Hence, $x\, \mid \,y$ = 01010111.
(iv). A bitwise XOR applied to a pair of bits returns a $1$ if the bits are different, and a $0$ otherwise.
Hence, $x \, \hat{} \, y$ = 01010001.
An interactive page on bitwise logic is available here 🔗 Bitwise Boolean Logic
End of Example 25 -
Summary
- This unit has introduced number systems and you should now be able to:
- convert between different number bases, in particular binary, decimal and hexadecimal.
- add and subtract binary numbers.
- understand how computers store and represent numbers.
- understand what is meant by unsigned and signed binary numbers.
- convert from decimal to two’s complement.
- convert from two’s complement to decimal.
- perform addition and subtraction for two’s complement representation.
- understand what is meant by two’s complement overflow.
- perform basic bitwise logical operations.
You should now attempt the tutorial exercises and Maple questions on GCU Learn.
In the next unit we introduce some basic concepts from number theory and look at their applications in the area of cryptography.