8. Applications of Number Theory in Cryptography

In this section we draw on the ideas from elementary number theory that were presented in the last two sections to demonstrate how these methods are applied in the field of cryptography. Some well-known ciphers are introduced and the relevant encryption and decryption processes are described.

8.1. Introduction

In short, cryptography is the study of encrypting and decrypting data using techniques from mathematics. The idea behind a cryptosystem (cipher system) is to conceal information from all that are not entitled to access it so that only the intended recipient(s) can access it. This concealment is done by replacing the information by what appears to be a sequence of random symbols. The essential determinant of the right of access to the information is ownership of a key needed to unlock the information from its “corrupted” form.

An alternative approach to using cryptography to make a message unreadable to a third party is to actually hide the message. This branch of science is called steganography and differs from cryptography in that with the latter it is obvious from the communication that it has been encrypted while with steganography messages do not attract attention as they may for example, be hidden in apparently ordinary image or text files. A more sophisticated approach to concealment combines the two methods by enciphering and then hiding the message. In our work we shall only be concerned with cryptography and before looking at a selection of well-known ciphers we present some basic terminology.

8.2. Basic Terminology

The basic layout of a (symmetric) cryptosystem is shown below.

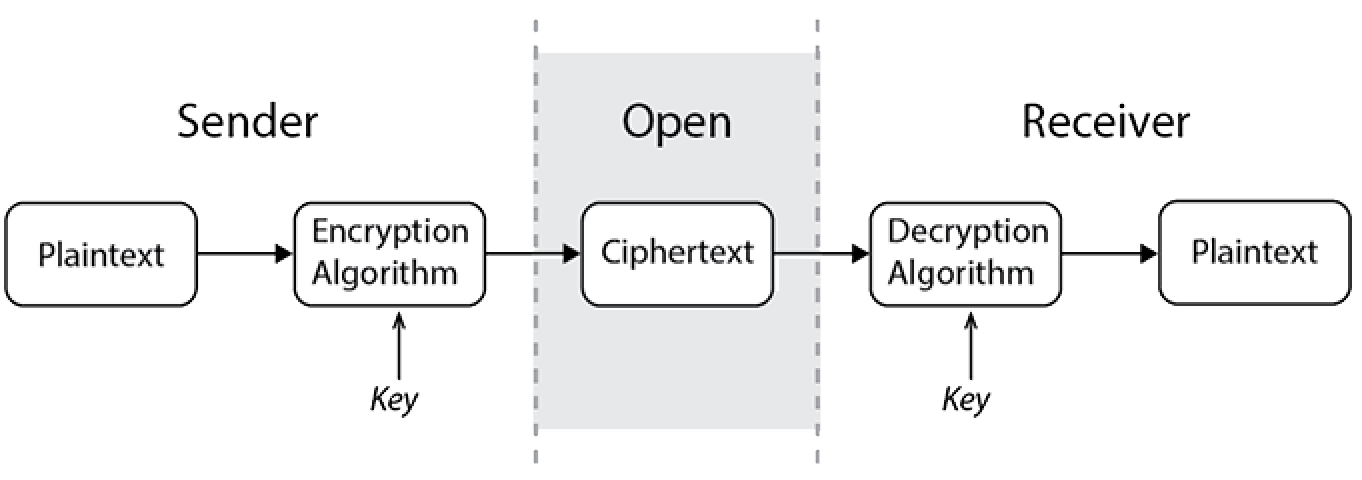
The basic layout of a symmetric cryptosystem Diagram

The encryption and decryption processes are composed of two parts: the algorithm and the key. In modern systems the algorithms are implemented on computers. The region between the dotted lines in the diagram, entitled “Open”, implies that anyone has access to the ciphertext. The assumption is that only the sender and receiver of the message have access outside of the delineated region.

We consider an encryption algorithm as a family of one-to-one functions from the set of all possible messages in a set $M$ to the set of all possible ciphertexts in a set $C$. The individual encryption functions are identified by their key $k$ from a set $K$.

Formally an encryption function is: $E_k: M \to C$ for some $k \in K$. Corresponding to each encryption function there is a decryption function: $D_{k^\prime} : C \to M$ satisfying $D_{k^\prime}(E_k(m)) = m$ for all possible $m \in M$ and $k’ \in K$.

The process of creating the ciphertext from the plaintext is called enciphering and of changing ciphertext back into plaintext is called deciphering.

Any person (or machine) in the “Open” region that is listening to the ciphertext transmissions is called an eavesdropper or interceptor. If the eavesdropper is trying to obtain the plaintext they are said to be attacking the system and if they succeed in obtaining the key that goes with the algorithm they are said to have broken, or cracked, the system.

The study of these systems is called cryptology and this is broken down into cryptography (the design of cryptographic systems) and cryptanalysis (the investigation of attacks on systems).

Summarising the above we have:

Plaintext:	The original message in readable text before it is encrypted. Plaintext also refers to the message after it has been retrieved, i.e. decrypted.
Cipher:	An algorithm for performing encryption and decryption.
Encryption:	A mathematical process, using knowledge of a key, for converting a plaintext message into ciphertext using a cipher.
Ciphertext:	A string of unreadable apparently random symbols resulting from encryption of the plaintext using a cipher.
Decryption:	The process of converting ciphertext back to plaintext using knowledge of a key.
Key:	A secret parameter which can be altered to produce different ciphertexts from the same plaintext. A key is also required for decryption.
Cryptography:	The study of how to design and implement secrecy systems so that transmitted data can only be processed and read by those for whom it is intended.
Cryptanalysis:	The study of how to break codes, without knowing the key, and decipher ciphertext into plaintext.
Cryptosystem:	A system for encoding and decoding messages.
Cryptology:	The discipline concerned with the storage and communication of data in secrecy systems. Cryptology includes both cryptography and cryptanalysis.

8.3. Keys

Encryption procedures are represented by algorithms operating on plaintext. The algorithm incorporates a key as part of the encipherment process. The same algorithm can be used with different keys, making for robust security.

It is always assumed that an attacker knows the algorithm in use and that the security is entirely in the keys (this is referred to as Kerckhoff’s principle). If a system is dependent on the secrecy of the algorithm; then anyone involved in using/designing/implementing the algorithm is a point of weakness (an ex-employee for example). Once the operation of such an algorithm is exposed then not only are all future texts potentially compromised (unless the system is changed immediately, which requires operators to know the break in security has taken place) but all previous ciphertexts are definitely compromised!

Given that the security of the cryptosystem is in the key, it must be arranged so that it is hard to find the key by a trial and error approach (a brute force attack). A good cryptosystem allows for a very large number of keys.

8.3.1. Symmetric and Asymmetric Cryptography

We distinguish between two types of cryptosystem based on how the enciphering and deciphering keys are related.

Symmetric Cryptography

For symmetric systems, as in the figure shown above, the key is considered to be the “same” for both the encryption and decryption processes and known to both the sender and receiver. Actually this is not literally true but the understanding is that the keys are so closely related that knowledge of one implies knowledge of the other. For example, when we discuss the Caesar cipher the enciphering key is a shift by $n$ which implies the deciphering key will be a shift by $– n$.

Asymmetric (Public Key) Cryptography

In contrast, asymmetric cryptography uses two keys, which while related, are such that knowledge of the enciphering key does not give knowledge of the deciphering key. For asymmetric systems such as the RSA, discussed later, the keys are different but clearly they need to be related for the system to work: it is the case that the relationship between the two keys is simply too difficult to break.

8.4. A Selection of Ciphers

In the remainder of this section we look at some well-known ciphers and present examples of how to encrypt plaintext and decrypt the resulting ciphertext using these ciphers.

8.4.1. Monoalphabetic Substitution Ciphers - Caesar Cipher

A monoalphabetic substitution cipher involves replacing each letter in an alphabet by a different letter in the same alphabet (or from a different alphabet). The deciphering involves replacing the substituted letter with its original value.

The simplest example of a monoalphabetic substitution cipher is the Caesar cipher which dates back to the time of Julius Caesar who apparently used it to communicate with his military generals. The modern day versions of this cipher were introduced in the late 1970s but are essentially based on the same ideas as that of the original version used by Caesar.

The Caesar cipher is essentially a shift cipher and involves substituting each individual letter in the original message (plaintext) by another letter from a specified number of places to the right or left in the alphabet. Julius Caesar used a right shift of $3$ so that each letter was replaced by the letter three places to its right in the alphabet. To illustrate the algorithm mathematically we first translate the $26$ letters ( A to Z ) in the standard English alphabet to their corresponding integer representations from 0 to 25. Using this approach we obtain the coding table for $\mathbb{Z}_{26}$. The shift is then applied and the ciphertext is obtained using modular arithmetic.

For example, if $x$ is defined to be the numerical equivalent of a letter in the plaintext and $y$ is the numerical equivalent of the corresponding letter in the ciphertext, then we calculate $y$ as follows:

$y ( x ) \equiv ( x + 3 )(mod\, 26). $

The key in this case is given by the amount of shift, i.e. $3$. Taking each plaintext letter from A to Z and applying the rule gives the ciphertext correspondence shown in the table below.

Plaintext	A	B	C	D	E	F	G	H	I	J	K	L	M	N	O	P	Q	R	S	T	U	V	W	X	Y	Z
Number, $x$	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25
Number, $y$	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	0	1	2
Ciphertext	D	E	F	G	H	I	J	K	L	M	N	O	P	Q	R	S	T	U	V	W	X	Y	Z	A	B	C

The procedure for encrypting letters, and generating the table, is defined as follows:

$\text{A}: y ( 0 ) \equiv ( 0 + 3 )(mod\, 26) = 3 \to \text{D}$

$\text{B}: y ( 1 ) \equiv ( 1 + 3 )(mod\, 26) \equiv 4(mod\, 26) = 4 \to \text{E}$

......................................................................

$\text{X}: y ( 23 ) \equiv ( 23 + 3 )(mod\, 26) \equiv 26(mod\, 26) = 0 \to \text{A}$

$\text{Y}: y ( 24 ) \equiv ( 24 + 3 )(mod\, 26) \equiv 27(mod\, 26) = 1 \to \text{B}$

$\text{Z} : y ( 25 ) \equiv ( 25 + 3 )(mod\, 26) \equiv 28(mod\, 26) = 2 \to \text{C}$

Note that the shift can take values other than 3 as we shall illustrate shortly.

Decryption essentially reverses the encryption process by subtracting the shift value so that the numerical value of the plaintext letter is calculated using,

$x ( y ) \equiv ( y - 3 )(mod\, 26)$.

For example, if the ciphertext contained the letter Z we would decrypt using:

$\text{Z} : x( 25 ) \equiv ( 25 - 3 )(mod \,26) \equiv 22( mod\, 26 ) = 22 \to \text{W}$.

Example 35

A Caesar cipher is defined in $\mathbb{Z}_{26}$ by the rule:

$y \equiv ( x + 13 )( mod\, 26 )$

(i). Use the cipher to convert the plaintext message “GOODBYE” to ciphertext.

ii). Determine the inverse of the above cipher.

(iii). Use the result in part (ii) to verify your answer to part (i).

Solution

(i). We use the coding table for $\mathbb{Z}_{26}$ to obtain the numerical value $( x )$ of each plaintext letter. Applying the rule results in letters being shifted 13 units to the right. The coding table for $\mathbb{Z}_{26}$ converts the numerical values $( y )$ to the ciphertext “TAAQOLS”.

Plaintext	G	O	O	D	B	Y	E
$x$	6	14	14	3	1	24	4
$x + 13$	19	27	27	16	14	37	17
$y = (x + 13)(mod \, 26)$	19	1	1	16	14	11	17
Ciphertext	T	A	A	Q	O	L	S

(ii). The inverse cipher is given by: $x \equiv ( y - 13 )( mod\, 26 )$

(iii). Verification of part (i) involves decrypting the ciphertext “TAAQOLS”.

Ciphertext	T	A	A	Q	O	L	S
$y$	19	1	1	16	14	11	17
$y - 13$	6	-12	-12	3	1	-2	4
$(y - 13)(mod \, 26)$	6	14	14	3	1	24	4
Plaintext	G	O	O	D	B	Y	E

The final row of the table verifies the result as we have retrieved the original plaintext.

Watch the video of the link below for an example of a Caesar cipher:

📹 Monoalphabetic Shift/Caesar Cipher

The Caesar cipher belongs to the much larger family of affine ciphers that encrypt data using the rule

$y \equiv ( ax + b )( mod\; 26 ). $

Decryption is performed using $x = a^{-1}(y - b)( mod\; 26 )$ where $a^{-1}$ is the multiplicative inverse of a in $\mathbb{Z}_{26}$. Note that there are only $12$ invertible elements in $\mathbb{Z}_{26}$ – see Multiplicative Inverse Tables.

We have noted the Caesar cipher is one of the simplest ciphers and as a result is vulnerable to many forms of attack. One method used in the cryptanalysis of Caesar ciphers is to compare the frequency of letters appearing in the ciphertext with statistical data on the frequency of these letters in the English language.

The limitations of the Caesar cipher, and similar monoalphabetic ciphers, brings us to a class of ciphers called polyalphabetic ciphers.

End of Example 35

Coding Tables

Coding tables for $\mathbb{Z}_{26}$ and $\mathbb{Z}_{29}$ can be found at the links below:

$\mathbb{Z}_{26}$ coding table

$\mathbb{Z}_{29}$ coding table

Multiplicative Inverse Tables

Multiplicative Inverses in $\mathbb{Z}_{26}$

Not every number, $a$, in $\mathbb{Z}_{26}$ has a multiplicative inverse meaning that we are unable to find a value $a^{-1}$ such that $aa^{-1} \equiv 1 ( mod \;26 )$ for all $a$. Equivalently, for a number $a$ that does not have an inverse in $\mathbb{Z}_{26}$ the Cayley multiplication table will not include a $1$ in the row (and column) corresponding to $a$. The following table shows that there are only $12$ invertible elements in $\mathbb{Z}_{26}$.

Number $(a)$	1	3	5	7	9	11	15	17	19	21	23	25
Inverse $(a^{-1})$	1	9	21	15	3	19	7	23	11	5	17	25

Multiplicative Inverses in $\mathbb{Z}_{29}$

As $29$ is a prime number we are guaranteed that every number in $\mathbb{Z}_{29}$ will have a multiplicative inverse. Every row and column in the Cayley multiplication table for $\mathbb{Z}_{29}$ will contain a $1$. The table below shows the multiplicative inverses for all non-zero elements in $\mathbb{Z}_{29}$.

Inverses modulo 29
Number (a)	Inverse $(a^{-1})$
1	1
2	15
3	10
4	22
5	6
6	5
7	25
8	11
9	13
10	3
11	8
12	17
13	9
14	27
15	2
16	20
17	12
18	21
19	26
20	16
21	18
22	4
23	24
24	23
25	7
26	19
27	14
28	28

8.4.2. Polyalphabetic Substitution Ciphers - Viginère cipher

THIS SECTION IS OPTIONAL AND YOU MAY MOVE ON TO SECTION 8.4.3.

The most famous attempt to break up the frequency profile of the underlying plaintext language is the Viginère cipher which was invented in the 16th century by a Frenchman, Blaise de Vigenère. To overcome the weaknesses of encrytping individual characters, the Viginère cipher takes a block of plaintext letters, of a specified length, and substitutes it with a block of ciphertext letters of the same length. Rather than having each letter encrypted in the same manner every time this approach has the effect of varying the way in which letters are encrypted. The Viginère cipher is an example of a polyalphabetic substitution cipher.

We first demonstrate the Viginère cipher by means of an example using a look-up table (see next page) before presenting the mathematics involved. The Viginère cipher uses a table with the letters A to Z as row and column headers. The first row of the table also includes the letters A to Z. Successive rows of the table are formed by shifting the previous row one position to the left in a cyclic manner. Hence, the second row has the letter B as its first entry and A as its last (rightmost) entry. We note here that each row of the table actually corresponds to a Caesar cipher. The first row represents a shift of $0$, the second row a shift of $1$ and so on until the final row corresponds to a shift of $25$. To encrypt a plaintext message the Viginére cipher uses the table and a keyword whose letters are repeated to have the same length as the plaintext.

The Viginére table showing the letter “G” encrypts to “K” when using the keyword “EXAMS”

Example 36

Encrypt the plaintext message, “GLASGOW CALEDONIAN” using the keyword “EXAMS”.

Solution

: Write down the plaintext message, ignoring any spaces.; Write the keyword above the plaintext, repeating letters as many times as necessary.

Keyword

Plaintext

: Choose a plaintext letter and its corresponding keyword letter.; Keyword letters correspond to rows of the Viginère table and plaintext letters to columns.; For each plaintext letter, and its corresponding keyword letter, identify the letter at the associated row/column intersection. This letter is the ciphertext letter.

In this example the first plaintext letter is G and the corresponding keyword letter is E. We therefore select the row for E and the column for G to find the letter K at the row/column intersection. See the highlighted cells in the Viginère table. Hence, the plaintext letter G has been encrypted as K. Continuing in this manner, processing each letter in turn, we obtain the result below.

Keyword

Plaintext

Ciphertext

The plaintext message “GLASGOW CALEDONIAN” has been encrypted as “KIAEYST CMDIAOZAEK”

A point to note here is that the plaintext contained three occurrences of the letter “A” which have been encrypted as three different letters, “A”, “M” and “E”. This example highlights the strength of the Viginère cipher against letter frequency analysis. It is clearly an improvement on the Caesar cipher which encrypts each occurrence of a plaintext letter to the same ciphertext letter every time.

To illustrate the decryption process we apply the method to decrypt the first letter of the ciphertext, i.e. K.: The first letter in the ciphertext, K, corresponds to the letter E in the keyword.; In the row for E, find K.; The column header for the column containing K is the plaintext, i.e. G. Refer to the highlighted cells in the diagram.

The Viginére table showing the letter “K” decrypts to “G” when using the keyword “EXAMS”

Watch the video at the following link:

📹 Polyalphabetic cipher

End of Example 36

We now take a brief look at the mathematics behind the Viginère cipher.

Suppose the keyword, of length $n$, is given by: $w_1\; w_2 \dots w_n$. Let the numerical equivalents ( obtained from the coding table for $\mathbb{Z}_{26}$ ) of letters in the keyword be: $k_1,\, k_2 , \dots, k_n$. The term “numerical equivalent” refers to the numerical location of a letter in the English alphabet starting with the letter A at location 0 (zero).

To encrypt a plaintext message:: Split the plaintext into blocks of length $n$, i.e. same length as the keyword.; Let the numerical equivalents of the letters in a given block be $m_1, m_2 , \dots, m_n$.; Generate a block of ciphertext of length $n$. The numerical equivalents of letters in the ciphertext are represented by $c_1, c_2 , \dots, c_n$ where $c_i \equiv ( k_i + m_i )( mod\; 26 )$, with $0 \le c_i \le 25$ and $i = 1, 2, \dots , n$.

The procedure is illustrated for the previous example.

From the coding table for $\mathbb{Z}_{26}$ the numerical equivalents ( $m_i$ ) of letters in the plaintext, “GLASGOW CALEDONIAN” are

and the numerical equivalents ( $k_i$ ) of letters in the keyword “EXAMS” are:

Calculating the letters in the encrypted message gives:

$c_1 = m_1 + k_1 = 6 + 4 \equiv 10( mod\; 26 )$

$c_2 = m_2 + k_2 = 11 + 23 = 34 \equiv 8( mod \;26 )$

$c_3 = m_3 + k_3 = 0 + 0 \equiv 0( mod\; 26 )$

$c_4 = m_4 + k_4 = 18 + 12 = 30 \equiv 4( mod\; 26 )$

$c_5 = m_5 + k_5 = 6 + 18 \equiv 24( mod\; 26 )$

$c_6 = m_6 + k_1 = 14 + 4 \equiv 18( mod\; 26 )$

$c_7 = m_7 + k_2 = 22 + 23 = 45 \equiv 19( mod\; 26 )$

$c_8 = m_8 + k_3 = 2 + 0 \equiv 2( mod\; 26 )$

$c_9 = m_9 + k_4 = 0 + 12 \equiv 12( mod\; 26 )$

$c_{10} = m_{10} + k_5 = 11 + 18 = 29 \equiv 3( mod\; 26 )$

$c_{11} = m_{11} + k_1 = 4 + 4 \equiv 8( mod\; 26 )$

$c_{12} = m_{12} + k_2 = 3 + 23 = 26 \equiv 0( mod\; 26 )$

$c_{13} = m_{13} + k_3 = 14 + 0 \equiv 14( mod\; 26 )$

$c_{14} = m_{14} + k_4 = 13 + 12 \equiv 25( mod\; 26 )$

$c_{15} = m_{15} + k_5 = 8 + 18 = 26 \equiv 0( mod\; 26 )$

$c_{16} = m_{16} + k_1 = 0 + 4 \equiv 4( mod\; 26 )$

$c_{17} = m_{17} + k_2 = 13 + 23 = 36 \equiv 10( mod\; 26 )$

We convert these numerical equivalents ( $c_i$ ) to letters using the coding table for $\mathbb{Z}_{26}$ giving:

10	8	0	4	24	18	19	2	12	3	8	0	14	25	0	4	10
K	I	A	E	Y	S	T	C	M	D	I	A	O	Z	A	E	K

Hence, as obtained previously using the Viginère table the plaintext message “GLASGOW CALEDONIAN” has been encrypted as “KIAEYST CMDIAOZAEK”

To decrypt the ciphertext we calculate as follows:

$m_1 = c_1 - k_1 = 10 - 4 \equiv 6( mod\; 26 )$

$m_2 = c_2 - k_2 = 8 - 23 = -15 \equiv 11 ( mod\; 26 )$

Continuing in this way we obtain

which translates to “GLASGOW CALEDONIAN” as expected.

For about 300 years the Viginère cipher was believed to be unbreakable and it was used extensively to encrypt sensitive data. However, by the mid-19th century the English scientist Charles Babbage and the Polish cryptographer Friedrich Kasiski had independently developed a method for cracking the cipher.

Go to this link to try some examples of encrypting and decrypting using the Viginère cipher.

🔗 https://crypto.interactive-maths.com/vigenegravere-cipher.html#encrypt

8.4.3. Block Ciphers - Hill Cipher

The main problem with substitution ciphers, such as the Casear cipher, is that they preserve the frequencies of individual letters and are therefore relatively easy to break. Over the years as work in the area of cryptography grew more sophisticated ciphers were developed that included more advanced mathematics. In this section we describe a cipher which is primarily of historical interest, but is useful in that it brings to light many issues that relate to modern cipher systems.

The Hill cipher was invented in 1929 by the American mathematician Lester S. Hill and is a type of polygraphic cipher which has as its key a square matrix operating with modular arithmetic. The plaintext message is broken down into blocks and these blocks are converted into column vectors. We note here that, for obvious reasons, Hill ciphers are also referred to as block ciphers. The encipherment process involves multiplying the vectors by the key matrix. The Hill Cipher encrypts blocks of letters simultaneously. For our purposes we shall use a Hill 2-cipher so that the key is a $2 \times 2$ matrix and plaintext is divided into vectors, of length two, i.e. two letters. It is relatively straightforward to generalise this encryption scheme to larger blocks of letters.

In the earlier unit on matrices we demonstrated, through an example, how matrix algebra, operating modulo $26$, is used to encrypt and decrypt a numerical message. The technique is now extended to encrypt letters from a selected alphabet. We could, as for the previous ciphers, use the standard English alphabet so that we are working modulo $26$. However, using a composite number makes the Hill cipher significantly harder to work with and care must be taken when selecting the key matrix to make sure that it is invertible as not every number in $\mathbb{Z}_{26}$ has a multiplicative inverse. To overcome the problem an alphabet of size $29$ , the smallest prime after $26$, can be used as this guarantees the key matrix is invertible modulo $29$. Every number in $\mathbb{Z}_{29}$ has an inverse as $29$ is a prime number. The alphabet we shall use is the standard English alphabet along with the three characters: “$.$”; “$?$” and “ $␣$; ”, i.e. full stop, question mark and space respectively.

Example 37

A Hill 2-cipher operates over $\mathbb{Z}_{29}$ with key matrix,

$A = \pmatrix{ 3 & 5 \\ 4 & 7}$

By working with symbols from the coding table for $\mathbb{Z}_{29}$ answer the following:

(i). Use the matrix $A$ to encrypt the plaintext, “RAIN”.

(ii). Show that the inverse of the matrix $A$ is, $A^{-1} = \pmatrix{\;\,7 & 24 \\ 25 & \;\;3}$.

(iii). Decrypt the ciphertext, “M?VE”.

Solution

(i). From the coding table for $\mathbb{Z}_{29}$ the numerical values of the letters in “RAIN” are:

$17\;\;\;0\;\;\;8\;\;\;13$

Divide into blocks of length $2$. The first vector is $\pmatrix{17 \\ \;\,0}$ and the second vector is $\pmatrix{\;\,8 \\13}$.

To encrypt the message we multiply each vector by the matrix $A$ operating modulo $29$.

$\pmatrix{3 & 5 \\ 4 & 7}\pmatrix{17 \\ \;\,0} = \pmatrix{51 \\ 68} \equiv \pmatrix{22 \\ 10} (mod \; 29)$

$\pmatrix{3 & 5 \\ 4 & 7}\pmatrix{\;\,8 \\ 13} = \pmatrix{\;\,89 \\ 123} \equiv \pmatrix{2 \\ 7}(mod \; 29)$

The numerical values corresponding to the ciphertext are therefore, $22 \;\; 10 \;\; 2 \;\; 7$ which, using the coding table for $\mathbb{Z}_{29}$ gives the ciphertext, “WKCH”.

(ii). Calculating the matrix product $A^{-1}\;\; A$ modulo $29$ should produce the identity matrix.

$A^{-1} A = \pmatrix{\;\,7 & 24 \\ 25 & \;\,3}\pmatrix{3 & 5 \\ 4 & 7} = \pmatrix{146 & \;\,87 \\ 203 & 117} \equiv \pmatrix{1 & 0 \\0 & 1}(mod \; 29)$ as required.

Alternatively, use the table of multiplicative inverses for $\mathbb{Z}_{29}$ giving

$A^{-1} = {\Large\frac{1}{(3 \times 7 - 5 \times 4)}} \pmatrix{\;\,7 & -5 \\-4 & \;\;\,3} \equiv \pmatrix{\;\,7 & 24 \\25 & \;\, 3}(mod \;29)$ as required.

(iii). The coding table for $\mathbb{Z}_{29}$ gives the numerical values of the letters in “M?VE” as:

$12\;\;\;27\;\;\;21\;\;\;4$

Divide into blocks of length $2$. The first vector is $\pmatrix{12 \\ 27}$ and the second vector is $\pmatrix{21 \\ \;\,4}$.

To decrypt the message we multiply each vector by the matrix $A^{-1}$ operating modulo $29$.

To simplify matters a little we can combine the vectors into a matrix

$\pmatrix{\;\,7 & 24 \\ 25 & \;\, 3}\pmatrix{12 & 21 \\ 27 & \;\, 4} = \pmatrix{732 & 243 \\ 381 & 537} \equiv \pmatrix{7 & 11 \\ 4 & 15}(mod \; 29)$

The numerical values corresponding to the plaintext are therefore, $7 \;\; 4 \;\; 11 \;\; 15$ which, using the coding table for $\mathbb{Z}_{29}$, gives the plaintext, “HELP”.

The answer can be checked by encrypting the plaintext “HELP” to hopefully obtain the ciphertext “M?VE”. We evaluate,

$\pmatrix{3 & 5 \\ 4 & 7}\pmatrix{7 & 11 \\ 4 & 15} = \pmatrix{41 & 108 \\ 56 & 149} \equiv \pmatrix{12 & 21 \\ 27 & \;\,4}(mod \; 29)$

The ciphertext corresponding to, $12 \;\; 27 \;\; 21 \;\; 4$ is “M?VE” as required.

End of Example 37

Watch the video at the following link.

📹 Polygraphic Part 2 - Hill Ciphers Examples/Encryption/Decryption

A major disadvantage of character and simple block ciphers is that if a cryptanalyst can access even a small amount of the plaintext message and the corresponding ciphertext then there is a very good chance that using frequency analysis he/she will be able to find the key. The next section looks at exponential ciphers which are less vulnerable to frequency analysis than character and block ciphers.

8.4.4. Exponential Ciphers

THIS SECTION IS OPTIONAL AND YOU MAY MOVE ON TO SECTION 8.5.

Exponential ciphers are defined on the set of integers $\mathbb{Z}_p = \{{1, 2, \dots , p - 1}\}$ where $p$ is a prime number. Plaintext messages, in numerical form, are encrypted using the rule

$c \equiv m^k (mod \; p)$

where $k$ in $\mathbb{Z}_{p-1}$ is relatively prime with $p - 1$, $m$ is a block of plaintext and $c$ is the corresponding ciphertext.

To decrypt the transmitted ciphertext the rule has the form

$m \equiv c^{k^\prime} (mod \; p)$

where $k^\prime$ is the multiplicative inverse of $k$ in $\mathbb{Z}_{p-1}$.

The process is best illustrated with an example.

Example 38

Define $p = 853$ so that $p - 1 = 852$ and take $k = 59$.

Check the conditions for an exponential cipher are satisfied:: $p = 853$ is a prime number.; $k = 59$ is in $\mathbb{Z}_{852}$.; $k = 59$ is relatively prime with $p - 1 = 852$, i.e. gcd$( 59, 852 ) = 1$.

The exponential cipher in this case is therefore given by,

$c \equiv m^{59} ( mod\; 853 )$.

Suppose we want to encrypt the message, “$101\; 271\; 046\; \dots$”.

Split the message into blocks of three digits and encrypt each block .

First encrypt the three digit block, $m = 101$ using,

$c \equiv 101^{59} ( mod\;853)$.

Use repeated squaring (details are given at the end of the example) to give:

$c \equiv 101^{59} \equiv 312 ( mod \;853)$

The next three digit block, $m = 271$ is encrypted using, $c \equiv 271^{59} ( mod\;853 )$ to give:

$ c \equiv 271^{59} \equiv 749 ( mod\; 853).$

The last three digit block, $m = 046$ is encrypted using, $c \equiv 046^{59} ( mod \;853 )$ to give:

$ c \equiv 046^{59} \equiv 150 ( mod\; 853). $

Hence, the encrypted message is “$312\; 749\; 150\; \dots $”.

As noted earlier, the decryption rule is $m \equiv c^{k’} (mod\; p )$ where $k’$ is the multiplicative inverse of $k$ in $\mathbb{Z}_{p – 1}$. To find $k’$ we can use the Extended Euclidean Algorithm giving $k’ = 491$.

It is relatively straightforward to check that $59 \times 491 \equiv 1mod(852)$. Note that we use mod $852$ and not mod $853$.

So, the decryption rule in this example is $m \equiv c^{491} ( mod\; 853)$ and we decrypt in blocks of $3$, using repeated squaring, in a similar manner to the encryption process.

The method works as the sender knows the exponent $59$ while the receiver knows the exponent $491$ and both know the prime number $853$.

Details of Repeated Squaring

Evaluate $101^{59} ( mod\; 853 )$ .

Write the exponent $(59)$ as a sum of powers of $2$:

$59 = 32 + 16 + 8 + 2 + 1$.

Working modulo $853$, repeatedly square $101$ to find $101^{2^k}$ for all $k$ such that $2^k < 59$.

$101^1 \equiv 101 ( mod\; 853 )$

$101^2 \equiv 818 ( mod\; 853 )$

$101^4 \equiv ( 101^2 )^2 \equiv 818^2 \equiv 372 ( mod\; 853 )$

$101^8 \equiv ( 101^4 )^2 \equiv 372^2 \equiv 198 ( mod\; 853 )$

$101^{16} \equiv ( 101^8 )^2 \equiv 198^2 \equiv 819 ( mod\; 853 )$

$101^{32} \equiv ( 101^{16} )^2 \equiv 819^2 \equiv 303 ( mod\; 853 ) $

Stop here as doubling the exponent again produces an exponent greater than 59.

Since $59 = 32 + 16 + 8 + 2 + 1$:

$101^{59} \equiv 101^{32 + 16 + 8 + 2 + 1}( mod\; 853 )$

$\equiv 101^{32} \times 101^{16} \times 101^8 \times 101^2 \times 101^1 ( mod\;853 )$

$\equiv 303 \times 819 \times 198 \times 818 \times 101 ( mod \;853 )$

$\equiv 312 ( mod\; 853 )$

Hence, $c \equiv 101^{59} \equiv 312 ( mod\; 853 )$.

End of Example 38

8.5. Public-Key Cryptography

The ciphers we have discussed up to now all use what is known as a symmetric key in that the same key is used for encryption and decryption. Public-key encryption uses two different keys, (asymmetric keys) a public key for encryption and a private key for decryption. Consider a cryptanalyst who intercepts a message in a traditional system, where the message was encrypted with a symmetric key, he/she may be able to decrypt this message. However, with a public-key system there is no need to secure the key used for the encryption as it will not decrypt the message, only the private key can do so. The private key will therefore never have to be transmitted as the encryption can be done without it. Note here that the two keys can swap as the private key can be used for encryption and the public key for decryption.

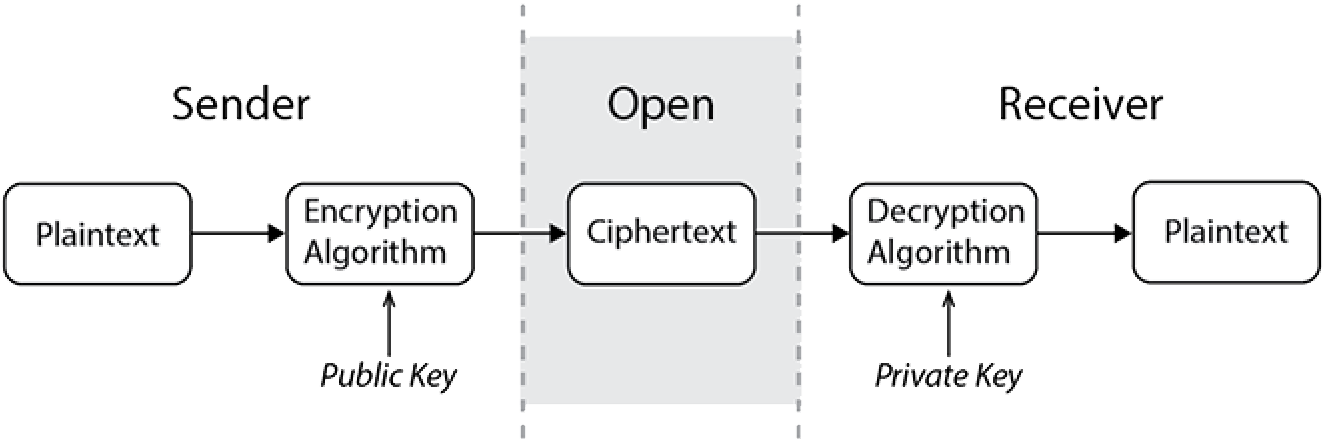
Have a look here for more information:

📹 Symmetric Key and Public Key Encryption

8.5.1. RSA Cipher

THIS SECTION IS OPTIONAL, YOU MAY OMIT AND GO TO THE SUMMARY.

The RSA cipher is named after its inventors, Rivest, Shamir and Adelmanan, who, while based at the Massachusetts Institute of Technology (MIT), first described the algorithm in 1978. It is an extremely powerful coding system, which to date has not been broken, and is widely used for sending sensitive data over insecure networks such as the internet. The RSA is based on the exponential cipher but uses two prime numbers as opposed to one. The strength of the cipher can be attributed to the difficulty in factoring large integers formed from the product of two prime numbers. While it is straightforward to multiply two massive primes ( with well over 100 digits each ) to obtain their product it is an extremely difficult task to reverse the process and from a given product identify which two primes formed this value - even using the power of modern super-computers this is a formidable task.

Plaintext messages, in numerical form, are encrypted using the rule

$c \equiv m^k (mod\; p\; q )$

where $k$ in $\mathbb{Z}_{(p-1)(q-1)}$ is relatively prime with $(p - 1)(q - 1)$, $m$ is a block of plaintext and $c$ is the corresponding ciphertext.

To decrypt the transmitted ciphertext the rule has the form

$m \equiv c^{k’} (mod\; p\; q )$

where $k’$ is the multiplicative inverse of $k$ in $\mathbb{Z}_{(p-1)(q-1)}$

The process is best illustrated with an example although we note that our values of $p$ and $q$ are significantly smaller than they would be in practice.

Go here for more information on the RSA cipher 📹 Public Key Cryptography: RSA Encryption Algorithm

Example 39

Choose the prime numbers, $p = 5$ and $q = 11$ so that $p - 1 = 4$ and $q - 1 = 10$.

Then $pq = 55$ and $(p - 1)(q - 1) = 40$.

$k = 27$ in $\mathbb{Z}_{40}$ is relatively prime with $(p - 1)(q - 1) = 40$.

The Extended Euclidean algorithm gives $k’ = 3$ as the multiplicative inverse of $k = 27$ in $\mathbb{Z}_{40}$.

The RSA cipher in this case is therefore given by,

$c \equiv m^{27} (mod \;55 ).$

Suppose we want to encrypt the message, “$17\; 23\; 46\; \dots $”.

Split the message into blocks of two digits and encrypt each block .

First encrypt the two digit block, $m = 17$ using repeated squaring to give:

$c \equiv 17^{27} \equiv 8 (mod \;55 )$

The next two digit block, $m = 23$ is encrypted to give:

$ c \equiv 23^{27} \equiv 12 (mod\; 55 ). $

The last two digit block, $m = 46$ is encrypted to give:

$c \equiv 46^{27} \equiv 51 (mod\; 55 ). $

Hence, the encrypted message is “$08\; 12\; 51 \; \dots $”.

The decryption rule is given by $m \equiv c^{k’} (mod\; p\; q )$ which in this case is $m \equiv c^3 (mod\; 55 )$.

Exercise: Decrypt the ciphertext “$08\; 12\; 51\; \dots $” to obtain the original plaintext.

End of Example 39

$\mathbb{Z}_{26}$
Plaintext Letter	Plaintext Number
A	0
B	1
C	2
D	3
E	4
F	5
G	6
H	7
I	8
J	9
K	10
L	11
M	12
N	13
O	14
P	15
Q	16
R	17
S	18
T	19
U	20
V	21
W	22
X	23
Y	24
Z	25

Number $(a)$	1	3	5	7	9	11	15	17	19	21	23	25
Inverse $(a^{-1})$	1	9	21	15	3	19	7	23	11	5	17	25

$\mathbb{Z}_{29}$
Plaintext Letter	Plaintext Number
A	0
B	1
C	2
D	3
E	4
F	5
G	6
H	7
I	8
J	9
K	10
L	11
M	12
N	13
O	14
P	15
Q	16
R	17
S	18
T	19
U	20
V	21
W	22
X	23
Y	24
Z	25
.	26
?	27
␣	28

Number (a)	Inverse $a^{-1}$
1	1
2	15
3	10
4	22
5	6
6	5
7	25
8	11
9	13
10	3
11	8
12	17
13	9
14	27
15	2
16	20
17	12
18	21
19	26
20	16
21	18
22	4
23	24
24	23
25	7
26	19
27	14
28	28

Summary

In this section we have described how the methods that we looked at earlier in the unit are applied in the field of cryptography. Basic terminology has been introduced and several different ciphers have been investigated in terms how they encrypt and decrypt data.

You should now be able to:

Know the basics of cryptography and be familiar with the associated terminology.

Appreciate the role different topics from number theory have in cryptography.

Encrypt plaintext, and decrypt the associated ciphertext, using the Caesar cipher.

OPTIONAL: Encrypt plaintext, and decrypt the associated ciphertext, using the Viginère cipher.

Encrypt plaintext, and decrypt the associated ciphertext, using the Hill cipher.

OPTIONAL: Encrypt plaintext, and decrypt the associated ciphertext, using the Exponential cipher.

Define public-key cryptography.

OPTIONAL: Appreciate the underlying techniques of RSA ciphers.

8. Applications of Number Theory in Cryptography

8.1. Introduction

8.2. Basic Terminology

8.3. Keys

8.3.1. Symmetric and Asymmetric Cryptography

8.4. A Selection of Ciphers

8.4.1. Monoalphabetic Substitution Ciphers - Caesar Cipher

Multiplicative Inverse Tables

8.4.2. Polyalphabetic Substitution Ciphers - Viginère cipher

8.4.3. Block Ciphers - Hill Cipher

8.4.4. Exponential Ciphers

8.5. Public-Key Cryptography

8.5.1. RSA Cipher

Summary