Previously we saw that the base 10 logarithm of 1000, written $log_{10}(1000)$, is 3 as we need to raise 10 to the power 3 to obtain 1000. We therefore have

$3 = log_{10}(1000)$  since   $1000 = 10^3$

Solve the following equations for $x$ by writing in exponential form.

Hint: use the fact that, $y = log_a(x) \implies x = a^y $

(i). $ log_2(x) = 6 \implies x = 2^6 = 64 $

(ii). $ log_3(x) = 4 \implies x = 3^4 = 81 $

(iii). $ log_{10}(x) = -2 \implies x = 10^{-2} = 0.01 $

(iv). $ ln(x) = 3 \implies x = e^3 $

(v). $ log_{1/6}(x) = -3 \implies x = \Big({\Large\frac{1}{6}}\Big)^{-3} = 6^3 = 216 $

(vi). $ log_{2\sqrt{3}}(x) = 6 \implies x = \Big(2 \sqrt{3}\Big)^6 = 2^6 (\sqrt{3})^6 = 64 \times 27 = 1728. $

Using the fact that, $y = log_{a}(x) \implies x = a^y$ determine the value of the base, $a$, in each of the following.

(i). $log_a(32) = 5 \implies a^5 = 32 \implies a = 2$.

(ii). $log_a(625) = 4 \implies a^4 = 625 \implies a = 5$.

(iii). $log_a(27) = 6 \implies a^6 = 27 \implies a = \sqrt{3}$

(iv). $ log_a(243) = -5 \implies a^{-5} = 243 \implies {\Large\frac{1}{a^5}} = 243 \implies a = {\Large\frac{1}{3}}$.

Calculate the following logarithms using a calculator giving the answer to 4 decimal places. Check your answer in each case.

(i). $log_{10}(2.3) = 0.3617 $ Check: $10^{0.3617} \approx 2.2999 $

(ii). $log_{10}(0.04) = -1.3979 $ Check: $10^{-1.3979} \approx 0.0400 $

(iii). $ln(2.3) = 0.8329 $ Check: $e^{0.8329} \approx 2.30000 $

(iv). $ln(0.04) = -3.2189 $ Check: $e^{-3.2189} \approx 0.0400 $

Some points worth noting here are:

The logarithms $ln$ and $log_{10}$ are not the same and produce different results – see Example 4. Care should therefore be taken when using a calculator that the correct button is selected.

Note that our checks do not always give the exact original value due to rounding errors that have been introduced when working to 4 decimal places.

(i). $ log_a(3 \times 4) = log_a(x) + log_a(y)$.

(ii). $ log_a(2) + log_a(6) = log_a(2 \times 6) = log_a(12) $.

(i). $ log_a\Big({\Large\frac{3}{4}}\Big) = log_a(3) - log_a(4)$.

(ii). $ log_a(24) - log_a(6) = log_a\Big({\Large\frac{24}{6}}\Big) = log_a(4) $.

(i). $ log_a(4^2) = 2log_a(4)$.

(ii). $ 3 log_a(4) = log_a(4^3) = log_a(64)$.

(i). $ log_{10}(10) = 1$. Since $10^1 = 10$

(ii). $ log_e(e) = 1$. Since $e^1 = e$

(i). $ log_{10}(1) = 0$. Since $10^0 = 10$

(ii). $ log_e(1) = 0$. Since $e^0 = 1$

(i). Show that $ log_a\Big({\Large\frac{1}{x^n}}\Big) = -n log_a(x)$.

Solution

$log_a\Big({\Large\frac{1}{x^n}}\Big) = log_a(x^{-n})$

$=$$-nlog_a(x)$.[Law 3]

Alternatively, $ log_a\Big({\Large\frac{1}{x^n}}\Big) = log_a(1) - log_a(x^n) $[Law 2]

$ = 0 - nlog_a(x)$[Law 5 & Law 3]

$=$$-nlog_a(x)$.

(ii). Show that $ log_a\Big({\Large\frac{x^m}{y^n}}\Big) = mlog_a(x) - nlog_a(y)$.

Solution

$log_a\Big({\Large\frac{x^m}{y^n}}\Big) = log_a(x^my^{-n}) $

$= log_a(x^m) + log_a(y^{-n}) $ [Law 1]

$=\;$$mlog_a(x)-nlog_a(y)$[Law 3]

Alternatively, $log_a\Big({\Large\frac{x^m}{y^n}}\Big) = log_a(x^m) - log_a(y^n) $[Law 2]

$=\;$$mlog_a(x)-nlog_a(y)$[Law 3]

(i). Expand $log_{10}\Big({\Large\frac{x^3y^4}{z^2}}\Big)$.

Solution

$log_{10}\Big({\Large\frac{x^3y^4}{z^2}}\Big) = log_{10}(x^3y^4) - log_{10}(z^2) $[Law 2]

$= log_{10}(x^3) + log_{10}(y^4) - log_{10}(z^2) $[Law 1]

$=\;$$3log_{10}(x)+4log_{10}(y)-2log_{10}(z)$[Law 3]

(ii). Express $4ln(x) + 6ln(y+z)- 3ln(y)$ as a single logarithm.

Solution

$4ln(x) + 6ln(y+z) - 3ln(y)$

$=ln(x^4) + ln(y + z)^6 - ln(y^3)$[Law 3]

$=ln[x^4(y + z)^6] - ln(y^3)$[Law 1]

$=\;$$ln\Big({\Large\frac{x^4(y+z)^6}{y^3}}\Big)$[Law 2]

(iii). Express $8log_9(x) - 6log_9(x + 3) + 2log_9(y)$ as a single logarithm.

Solution

$8log_9(x) - 6log_9(x + 3) + 2log_9(y)$

$= log_9(x^8) - log_9(x + 3)^6 + log_9(y^2)$[Law 3]

$= log_9\Big({\Large\frac{x^8}{(x + 3)^6}}\Big) + log_9(y^2)$[Law 2]

$=\;$$log_9\Big({\Large\frac{x^8y^2}{(x + 3)^6}}\Big)$[Law 1]

(iv). If $log_3(y) = 4 $ and $log_3(x) = 2 $ determine the numerical value of $log_3\bigg({\Large\frac{y^6}{\sqrt{x}}}\bigg) $

Solution

We simplify the expression using the laws of logs and substitute the given values.

$log_3\Big({\Large\frac{y^6}{\sqrt{x}}}\Big) = log_3(y^6) - log_3(x^{1/2})$[Law 2]

$= 6log_3(y) - {\Large\frac{1}{2}}log_3(x)$[Law 3]

$= 6 \times 4 - {\Large\frac{1}{2}} \times 2 $[substitute values]

$= 24 - 1$

$=\;$$\class{double}{2}$$\class{double}{3}$

(i). $log_{10}(10^x) = x$

(ii). $log_{e}(e^x) = ln(e^x) = x$

(i). $10^{log_{10}(x)} = x$

(ii). $e^{log_{e}(x)} = e^{ln(x)} = x$

Using Properties 1 and 2 solve the following equations giving your answers to 4 decimal places.

(i).    $10^{3x + 4} = 5 $

$log_{10}(10^{3x+4}) = log_{10}(5) $[Take log (base 10) of each side - Property 1]

$3x + 4 = log_{10}(5) $[Inverse property]

$x = {\Large\frac{1}{3}}(log_{10}(5) - 4) $

$x = - 1.1003$.[check: $10^{3 \times(-1.1003)+4}\approx 5$]

(ii).   $log_{10}(3x) =\; 2.4 $

$10^{log_{10}(3x)} = 10^{2.4} $[Exponentiate (base10) each side - Property 2]

$3x = 10^{2.4}$[inverse Property]

$x = {\Large\frac{10^{2.4}}{3}}$

$x = 83.7295$[check: $log_{10}( 3 \times 83.7925) \approx 2.4$]

(iii).    $ln(2x + 1) = 8$

$e^{ln(2x+1)}= e^8 $[Exponentiate (base $e$) each side - Property 2]

$2x + 1 = e^8$[inverse Property]

$ x = {\Large\frac{1}{2}}(e^8 - 1)$

$x = 1489.9790$[check: $ln(2 \times 1489.9790 + 1) \approx 8$]

(iv).    $ 2^{2x - 1} = 2.3 $

$ln(e^{2x-1}) = ln(2.3) $[Take log (base $e$) of each side - Property 1]

$2x - 1 = ln(2.3)$[inverse Property]

$x = {\Large\frac{1}{2}}(ln(2.3) + 1)$

$x = 0.9165$[check: $e^{2 \times 0.9165 - 1} \approx 2.3$ ]

Solve the following exponential equations for $x$, using your calculator to express the answers to 4 decimal places

Note that in this question you can use either the log base 10 ($log$) or the natural log ($ln$) buttons on your calculator and you will obtain the same answer.

(i).   $3^x = 100$

Solution

Take log to base 10 of both sides

$log(3^x) = log(100)$

$xlog(3) = log(100)$[ use Law 3 to bring the $x$ down ]

$x = {\Large\frac{log(100)}{log(3)}}$[ evaluate using a calculator ]

$x = 4.1918$[ check: $log(3^{4.1918}) \approx 100$ ].

(ii).   $12.02 = 4.23 + 3.1^{2x}$

Solution

The idea is to get the equation close to the form $a = b^x$

$12.02 - 4.23 = 3.1^{2x}$

$7.79 = 3.1^{2x}$

$log(7.79) = log(3.1^{2x})$

$log(7.79) = 2xlog(3.1)$

$x = {\Large\frac{log(7.79)}{2log(3.1)}}$

$x = 0.9072$

Exercise: Verify that the same results are obtained in (i) and (ii) using the natural logarithm.

Solve the following logarithmic equations for $x$. The validity of each solution must be checked to ensure that we are not taking the log of a non-positive number.

(i). $3log_a(5) + log_a(4) - log_a(2) - log_a(x)$.

$log_a(5^3) + log_a(4) - log_a(2) = log_a(x)$[ Law 3 ]

$log_a(5^3 \times 4) - log_a(2) = log_a(x) $[ Law 1 ]

$log_a\Big({\Large\frac{5^3 \times 4}{2}}\Big) = log_a(x)$[ Law 2 ]

$log_a(250) = log_a(x)$

$x = 250$

(ii). $log_4(x - 4) - log_4(8) = log_4(x + 9) - log_4(10)$

$log_4\Big({\Large\frac{x-4}{8}}\Big) = log_4\Big({\Large\frac{x+9}{10}}\Big)$[ apply Law 2 to both sides ]

${\Large\frac{x-4}{8}} = {\Large\frac{x+9}{10}}$[ equate contents of brackets ]

$10(x - 4) = 8( x + 9 )$[ cross-multiply ]

$10x - 40 = 8x + 72$[ expand brackets ]

$2x = 112$

$x = 56$

(iii). $2log_3(x) = log_3(2) + log_3(3x-4)$

$log_3(x^2) = log_3[2 \times (3x - 4)]$[ apply Law 3 to LHS & Law 1 to RHS]

$log_3(x^2) = log_3[6x - 8]$

$x^2 = 6x - 8$[ equate contents of brackets ]

$x^2 - 6x + 8 = 0$

$(x-2)(x-4) = 0$

$x = 2$ or $x = 4$[ both answers are valid ]

(iv). $log_2(x+4) - log_2(x-3) = 4$

$log_2\Big({\Large\frac{x+4}{x-3}}\Big) = 4$[ Law 2 ]

$2^{log_2({\Large\frac{x+4}{x-3}})}= 2^4$[ Exponentiate (base 2) each side - Property 2 ]

${\Large\frac{x+4}{x-3}} = 16$[ Inverse property ]

$x + 4 = 16(x - 3)$

$x + 4 = 16x - 48$

$17x = 52$

$x={\Large\frac{52}{17}}$[ Answer is valid ]

(v). $log_2(x - 2) + log_2(x + 1) = 2$

$log_2[(x - 2)(x + 1)] = 2$[ Law 1 ]

$log_2[x^2 - x - 2] = 2$[ expand brackets ]

$2^{log_2(x^2 - x - 2)} = 2^2$[ Exponentiate (base 2) each side - Property 2 ]

$x^2 - x - 2 = 4$[ Inverse property ]

$x^2 - x - 6 = 0$

$(x + 2)(x - 3) = 0$

$x = -2$ or $x = 3$

However, only $x = 3$ is valid as substituting $x = -2$ in the original expression will lead to taking the logarithm of a negative number in both expressions on the LHS.

Plot the functions $y = log_{10}(x)$ and $y = log_{0.1}(x)$ on the same graph.

Solution

We first generate a table for various values of $x$. For clarity purposes we restrict the plot to show the functions for values of $x$ from $0.05$ to $10$.

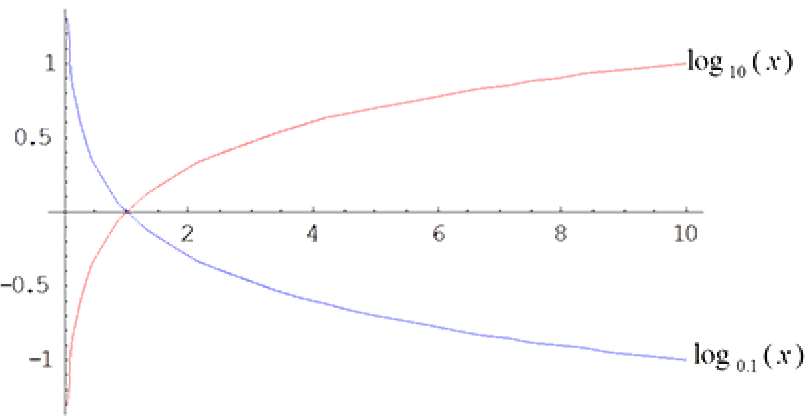
$x$	$0.001$	$0.01$	$0.1$	$1$	$10$	$100$	$1000$
$log_{10}(x)$	$-3$	$-2$	$-1$	$0$	$1$	$2$	$3$
$log_{0.1}(x)$	$3$	$2$	$1$	$0$	$-1$	$-2$	$-3$

Both functions are undefined for $x \leq 0$, i.e. we cannot take the log of a number less than or equal to zero.

Both graphs pass through the point (1, 0).

The graphs are mirror images of each other in the $x$-axis.

Plot the graphs of the function $y = log_a(x)$ for $a = 2$, $a = e$ and $a = 10$.

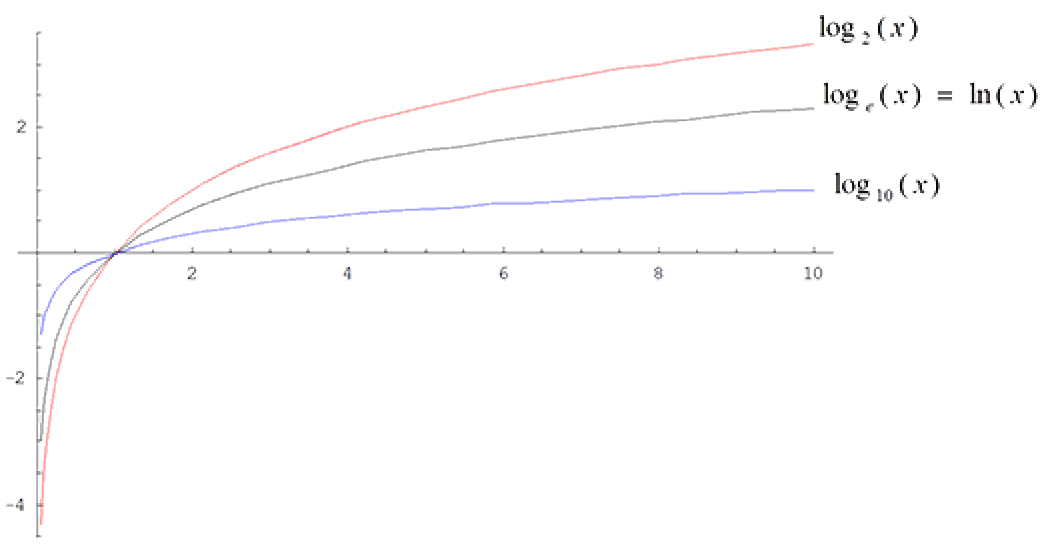
Properties to note from the graph are:

As $a > 1$ the functions are all increasing with the rate of increase slowing down the larger $x$ becomes.

The rate at which the graphs increase is greatest between $x = 0$ and $x = 1$.

The functions are positive for all values of $x > 1$ and negative for $x < 1$.

All graphs pass through the point (1, 0).

The graphs never cross the $y$-axis as $x$ can never equal $0$.

A bacterial culture follows a growth model given by

$P(t) = P_0e^{0.2554t}$

where $P_0$ is the initial population of 3000 and $P(t)$ is the size of the population at time $t$ hours.

(i). Determine the population size at time $t = 4$ hours.

(ii). If the culture medium can only support a population of 50000 determine the time, $T$ say, when the population reaches this value.

Solution

(i). Here $P_0 = 3000$ and $t = 4$ so the formula becomes

$P(4) = 3000e^{0.2554 \times 4}$

$= 8333$ bacteria to the nearest whole number.

Hence, after 4 hours the population size has grown to approximately 8333 bacteria.

(ii). Setting $t = T$ we require the value of $T$ for which $P(T) = 50000$.

Hence, $50000 = 3000e^{0.2554T}$ which simplifies to give $e^{0.2554T} = {\Large\frac{50}{3}}$.

Now solve for $T$ using the fact the logarithm function is the inverse of the exponential function.

$e^{0.3554T} = {\Large\frac{50}{3}}$

$ln\Big(e^{0.2554T}\Big) = ln\Big({\Large\frac{50}{4}}\Big)$ [ Take log (base $e$) of each side - Property 1 ]

$0.2554T = ln\Big({\Large\frac{50}{3}}\Big)$[ Inverse property ]

$T = \frac{1}{0.2554}ln\Big({\Large\frac{50}{3}}\Big)$

$T=11.0157$

The decay of the radioactive element radium is modelled by the formula

$A = A_0(0.5)^{{\Large\frac{t}{1620}}}$

where $A_0$ is the initial amount of radium and $A$ is the amount remaining after $t$ years.

(i). How much radium remains in a 1 kg sample after 1000 years?

(ii). How long would it take for a 1 kg sample to decay to 0.01 kg?

Solution

(i). Set $A_0 = 1, t = 1000$, in formula and evaluate:

$A = (0.5)^{{\Large\frac{1000}{1620}}} = \;$ $0.6519\; \text{kg}$

(ii). Set $A_0 = 1, A = 0.01$, in formula and solve for $t$ :

$0.01 = (0.5)^{{\Large\frac{t}{1620}}}$

$ln(0.5)^{{\Large\frac{t}{1620}}} = ln(0.01)$[ Take $ln$ of each side ]

${\Large\frac{t}{1620}}ln(0.5) = ln(0.01)$[ Law 3 ]

$t = {\Large\frac{1620\; ln(0.01)}{ln(0.5)}}$

$=\;$$10763 \; \text{years}$

Two computer algorithms, which solve the same problem, have complexity functions:

(i). $f(n) = n^{3/2}$

(ii). $g(n) = n log_2(n)$

Determine which algorithm is more efficient on a problem which has 10 000 steps.

Solution

Set $n = 10000$ and determine $f(10 000)$ and $g(10 000)$.

$f(10 000) = (10 000)^{3/2}$

$=\;$$\class{double}{1}$$\class{double}{0}$$\class{double}{0}$$\class{double}{0}$$\class{double}{0}$$\class{double}{0}$$\class{double}{0}$

$g(10 000) = 10 000log_2(10 000)$

$= 10 000log_2(10^4)$

$= 10 000 \times 4 log_2(10)$[ Law 3 ]

$= 40 000log_2(10)$

$= 40 000{\Large\frac{1}{log_{10}}(2)}$[ base switch rule – see below ]

$=\;$$\class{double}{1}$$\class{double}{3}$$\class{double}{2}$$\class{double}{8}$$\class{double}{7}$$\class{double}{7}$

As $g(10 000) < f(10 000)$ we use $g(n)$.

Note: The base switch rule gives that $log_a(b) = {\Large\frac{1}{log_b(a)}}$.

Here we wrote $log_2(10) = {\Large\frac{1}{log_{10}(2)}}$ so that we can evaluate the expression by calculator.

In a sorted list of keys to access data the binary search method has a complexity function of $g(n) = log_2(n)$ . In an unsorted list a particular linear search method has a complexity function of $f(n) = {\Large\frac{n}{2}}$.

For $n = 10, 10^2, 10^3, 10^4, ..., 10^9$ determine the values of $f(n)$ and $g(n)$.

Solution

$n$	$f(n)$	$g(n)$
10	5	3.3
100	50	6.6
1000	500	10.0
10 000	5000	13.3
$\dots$	$\dots$	$\dots$
1 000 000 000	500 000 000	29.9

For small values of $n$ it does not really matter which algorithm is used. For large values of $n$ we find that $g(n)$ is significantly more efficient than $f(n)$.