-
1. Introduction
In recent years graph theory has become established as an important area of mathematics and computer science. The origins of graph theory however can be traced back to Swiss mathematician Leonhard Euler and his work on the Königsberg bridges problem (1735), shown schematically in Figure 1.
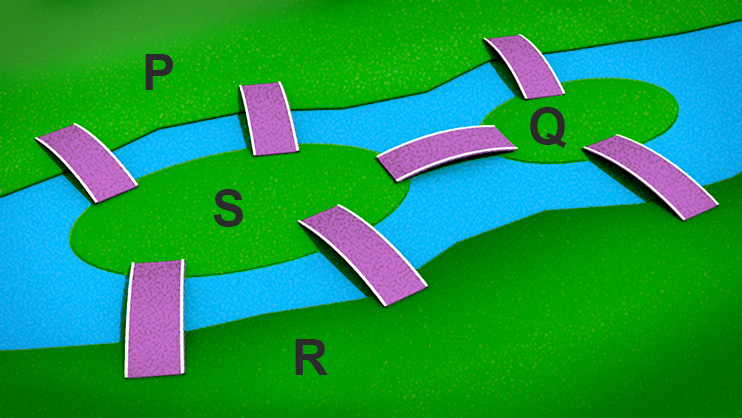
Figure 1: Bridges of Königsberg Königsberg was a city in 18th century Germany (it is now called Kaliningrad and is in western Russia) through which the river Pregel flowed. The city was built on both banks of the river and on two large islands in the middle of the river. Seven bridges were constructed so that the city’s inhabitants could travel between the four parts of the city; labelled P, Q, R and S in the diagram. The people wondered whether or not it was possible for someone to walk around the city in such a way that each bridge was crossed exactly once with the person ending up at their starting point. All attempts to do so ended in failure. In 1735 however Euler presented a solution to the problem by showing that it was impossible to perform such a journey. Euler reasoned that anyone standing on a land mass would need a way to get on and off. Therefore each land mass would require an even number of bridges. In Königsberg each land mass had an odd number of bridges explaining why all seven bridges could not be crossed without crossing one more than once.
In formulating his solution Euler simplified the bridge problem by representing each land mass as a point and each bridge as a line as shown in 📷 Figure 2, leading to the introduction of graph theory and the concept of an Eulerian graph. A closely related problem showed that if the journey started at one land mass and ended at another, crossing each bridge exactly once, then only those two land masses could have an odd number of bridges.
Now watch this video:
- Two other well-known problems from graph theory are:
- Graph Colouring Problem: How many colours do we need to colour a map so that every pair of countries with a shared border have different colours?
- Travelling Salesman Problem: Given a map of several cities and the roads between them, is it possible for a travelling salesman to visit (pass through) each of the cities exactly once?
- Some of the applications of graph theory include:
- communication network design
- planning airline flight routes
- using GPS to find the shortest path between two points
- design of electrical circuits
- modelling of the Worldwide Web.
X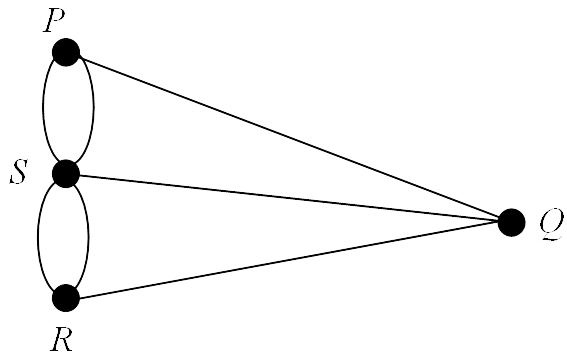
Figure 2: Graphical representation of the Königsberg bridge problem -
2. Definitions
Start by watching this video:
The Königsberg bridge problem can be represented diagramatically by means of a set of points and lines. The points $P$, $Q$, $R$ and $S$ are called vertices, the lines are called edges and the whole diagram is called a graph.

Figure 2: Graphical representation of the Königsberg bridge problem 2.1. Vertices and Edges
A graph, $G$, is a mathematical structure which consists of:
(i). a vertex set $V = V(G)$ whose elements are called vertices of $G$.
(ii). an edge set $E = E(G)$ of unordered pairs of distinct vertices called edges of $G$. Note that $E$ is actually a multiset in that some unordered pairs can be repeated to represent more than one edge joining two vertices.
(iii). a relation that associates with each edge two vertices, which are not necessarily distinct, called its endpoints.
Such a graph is denoted $G = \{V(G), E(G)\}$ , if we want to be specific about which graph $G$ we are referring to, or just simply $G = \{V, E\}$ .
Example 1
Consider the graph $G$ shown in the diagram below.
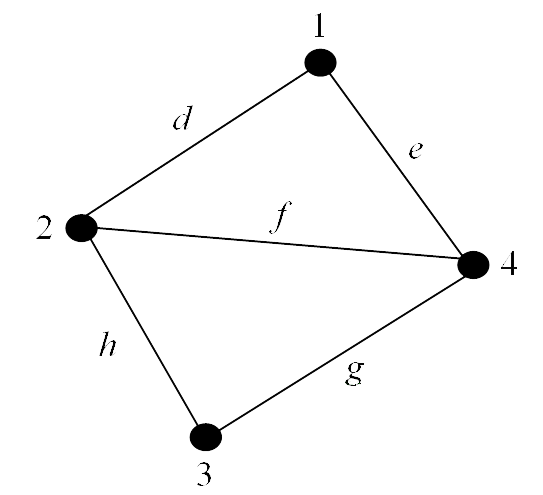
Figure 3: Graph with four vertices and five edges The set $V$ consists of the four vertices, $1$, $2$, $3$ and $4$, i.e. $V(G) = \{1, 2, 3, 4\}$.
The set $E$ consists of the five edges, $d = \{1, 2\}$, $e = \{1, 4\}$, $f = \{2, 4\}$, $g = \{3, 4\}$ and $h = \{2, 3\}$ , i.e. $E(G) = \{d, e, f, g, h\}$.
Hence, $G = \{V(G), E(G)\} = \{\{1, 2, 3, 4\}, \{d, e, f, g, h\}\}$.
Each edge is associated with two vertices called its endpoints.
For example, in Figure 3, vertices $1$ and $2$ are the endpoints of $d$ and $d$ is said to connect vertices $1$ and $2$.
End of Example 1An undirected graph is a graph in which the edges have no orientation. Hence, in an undirected graph the edge set is composed of unordered vertex pairs. In 📷 Figure 3 for example, the edge $\{1, 2\}$ is considered identical to the edge $\{2, 1\}$ .
An edge-endpoint function on a graph $G$ defines a correspondence between edges and their endpoints.
Example 2
The edge-endpoint function for the graph in 📷 Figure 3 is given in the following table:
Edge Endpoints $d$ $\{1,2\}$ $e$ $\{1,4\}$ $f$ $\{2,4\}$ $g$ $\{3,4\}$ $h$ $\{2,3\}$ End of Example 2If $X$ and $Y$ are vertices of a graph, $G$, then $X$ and $Y$ are said to be adjacent if they are joined by an edge.
An edge in a graph that joins two vertices is said to be incident to both vertices.
Example 3
- Referring to 📷 Figure 3, and the edge-endpoint table, we have the following adjacent vertices:
- vertices $1$ and $2$ are adjacent
- vertices $1$ and $4$ are adjacent
- vertices $2$ and $3$ are adjacent.
- vertices $2$ and $4$ are adjacent
- vertices $3$ and $4$ are adjacent
- The edges are incident with pairs of vertices as follows:
- edge $d$ is incident to vertices $1$ and $2$
- edge $e$ is incident to vertices $1$ and $4$.
- edge $f$ is incident to vertices $2$ and $4$
- edge $g$ is incident to vertices $3$ and $4$
- edge $h$ is incident to vertices $2$ and $3$.
End of Example 3Two edges connecting the same vertices are called multiple or parallel edges. In Figure 4 edges $f$ and $g$ are parallel edges.
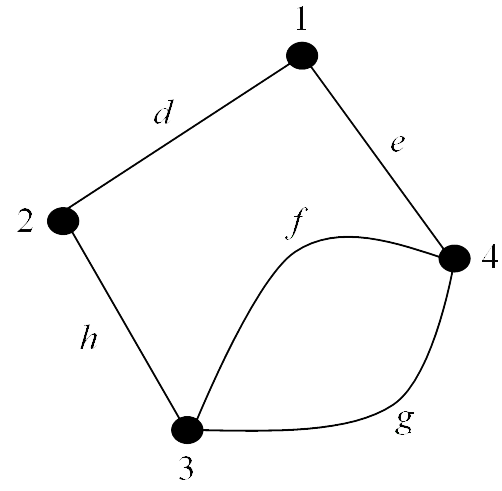
Figure 4: Graph containing parallel edges Graphs like the one shown here, containing parallel edges, are called multigraphs and we shall look at these in more detail later in the unit.
The order of a graph $G$, denoted $\mid V(G)\mid$, is the number of vertices contained in $G$.
In 📷 Figure 3, $\mid V(G) \mid = 4$.
The size of a graph $G$, denoted $\mid E(G)\mid $, is the number of edges contained in $G$.
In 📷 Figure 3, $\mid E(G)\mid = 5$.
The degree of a vertex $X$, written $deg(X)$, is the number of edges in $G$ that are incident with $X$.
In 📷 Figure 3, $deg(1) = 2$, $deg(2) = 3$, $deg(3) = 2$ and $deg(4) = 3$.
Any vertex of degree zero is called an isolated vertex and a vertex of degree one is an end-vertex.
Example 4
In the graph below vertex $5$ is an isolated vertex and vertex $3$ is an end-vertex.
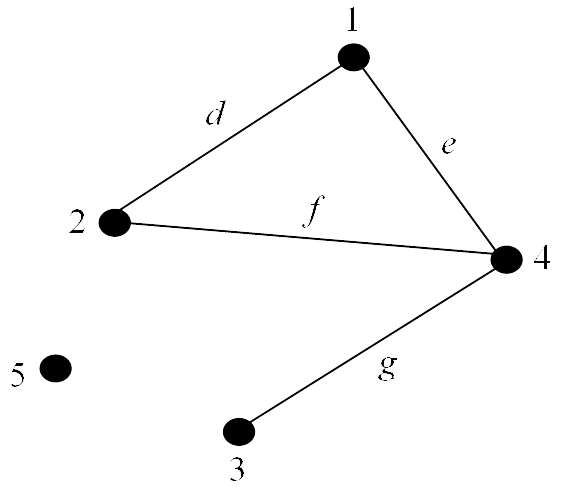
Figure 5: Graph containing an isolated vertex End of Example 4A vertex is said to be even or odd according to whether its degree is an even or odd number. In 📷 Figure 3 vertices $2$ and $4$ are odd while vertices $1$ and $3$ are even.
If the degrees of all the vertices in a graph, $G$, are summed then the result is an even number. Furthermore, this degree is twice the number of edges, as each edge contributes $2$ to the total sum. We have the following lemma:
The Handshaking Lemma
In any undirected graph the sum of the vertex degrees is equal to twice the number of edges, i.e.
$$\sum_{X \in V[G]} deg(X) = 2 \mid E(G) \mid .$$
Proof: In a graph $G$ an arbitrary edge $\{X, Y\}$ contributes $1$ to $deg(X)$ and $1$ to $deg(Y)$. Hence the degree sum for the graph is even.
Note: A corollary of the Handshaking Lemma states that the number of odd vertices in a graph must be even. So, for example, we cannot have a graph with $5$ even vertices and $5$ odd vertices as the degree sum would be an odd number, contradicting the Handshaking Lemma.
Watch the Handshaking Lemma video at:
📹 Sum of Degrees is ALWAYS Twice the Number of Edges
The degree sequence of an undirected graph $G$ is a bracketed list of the degrees of all the vertices written in ascending order with repetition as necessary.
Example 5
The degree sequence of the graph in the diagram below is $( 1, 2, 2, 3, 4 )$.
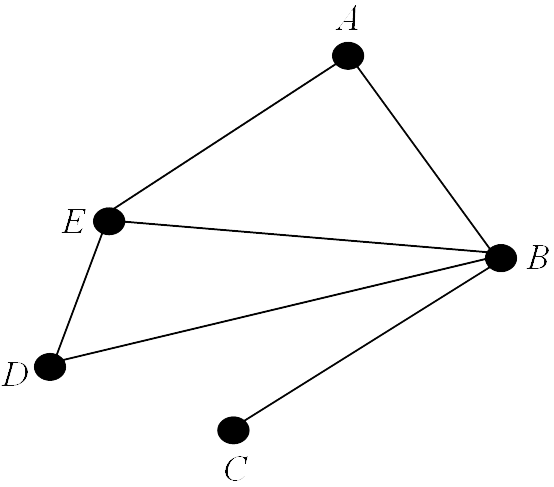
Note that some texts define the degree sequence of a graph as the degrees of the vertices written in descending order with repetition as necessary. In the above case we would have $( 4, 3, 2, 2, 1 )$.
End of Example 52.2. Connected Graphs
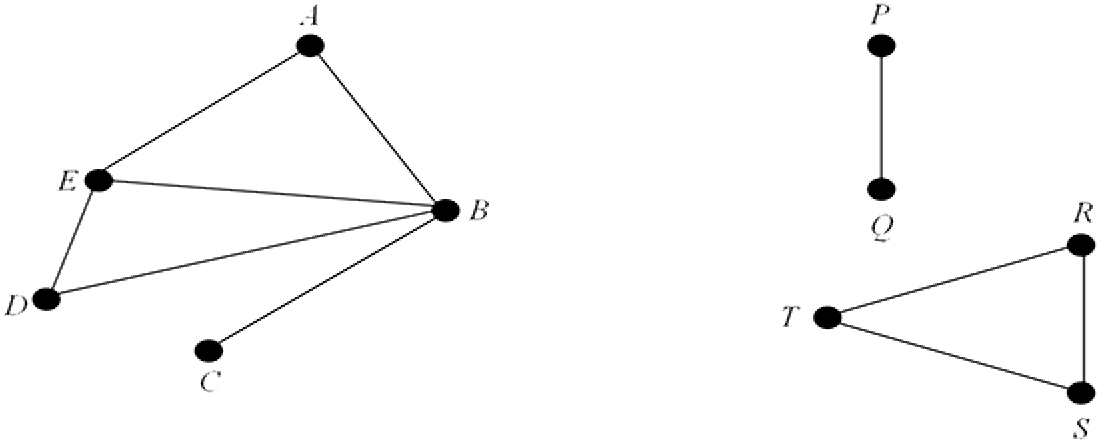
A graph is said to be connected if it cannot be expressed as the union of two graphs. If a graph is not connected it is said to be disconnected. The graph on the left is connected as it is “in one piece” while the graph on the right is disconnected as it contains two distinct components. See Section 4 for an alternative definition of connected.
2.2.1. Cut-Points and Bridges
A vertex is a cut-vertex, if removal of that vertex (and the edges through it) disconnects the graph. A cut-vertex is also called a cut-point or an articulation point.
Example 6
In the graph on the left vertex 2 is a cut-vertex as its removal disconnects the graph. The resulting graph, on the right, has two connected components. Vertex 6 is also a cut-vertex.
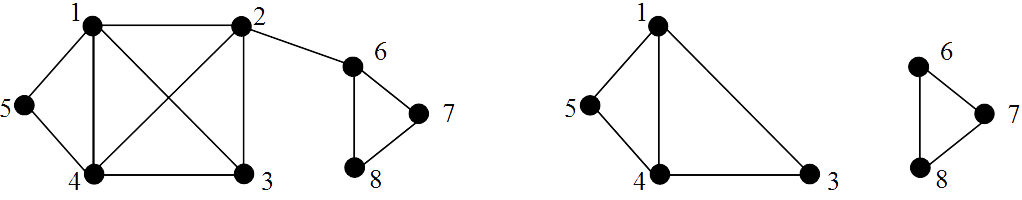
An edge is a bridge (or isthmus) if removal of that edge disconnects the graph.
Here edge $\{2, 6\}$ is a bridge as its removal disconnects the graph.
End of Example 6X
-
3. Graph Structures
In this section we briefly look at different types of graphs.
3.1. Regular Graphs
A graph $G$ is regular if all vertices of $G$ have the same degree. A regular graph where all vertices have degree $k$ is referred to as a $k$-regular graph.
Example 7
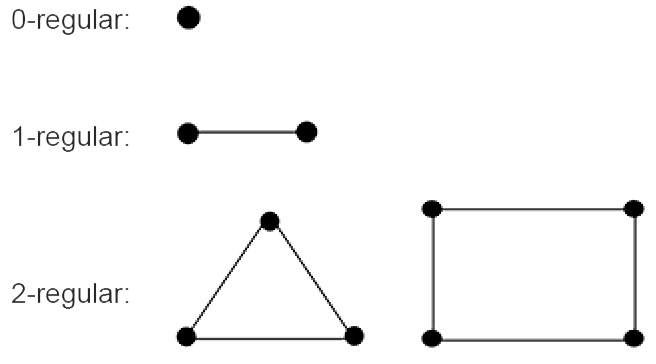
The graph on the left is called a 2-regular graph on 3 vertices and the one on the right is a 2-regular graph on 4 vertices.
Exercise: Sketch a 2-regular graph on 5 vertices.
Notes
(i). The Handshaking Lemma tells us that the total degree of any graph is an even number, i.e. twice the number of edges. Hence, it is impossible to construct a k-regular graph, where k is odd, on an odd number of vertices. For example, we cannot have a 3-regular graph on 5 vertices as this would give a degree sum of 15, violating the Handshaking Lemma.
(ii). A 0-regular graph (see above) is called an empty graph.
(iii). Cycle graphs (see Section 3.3) are 2-regular graphs.
(iv). 3-regular graphs are called a cubic graphs.
There is only one 3-regular graph on 4 vertices. Can you sketch it?
There are two 3-regular graphs on 6 vertices. Can you sketch them?
There is no 3-regular graph on 7 vertices. Why?End of Example 73.2. Complete Graphs
A complete graph, denoted $K_n$, is a graph with $n$ vertices all of which are adjacent to each other.
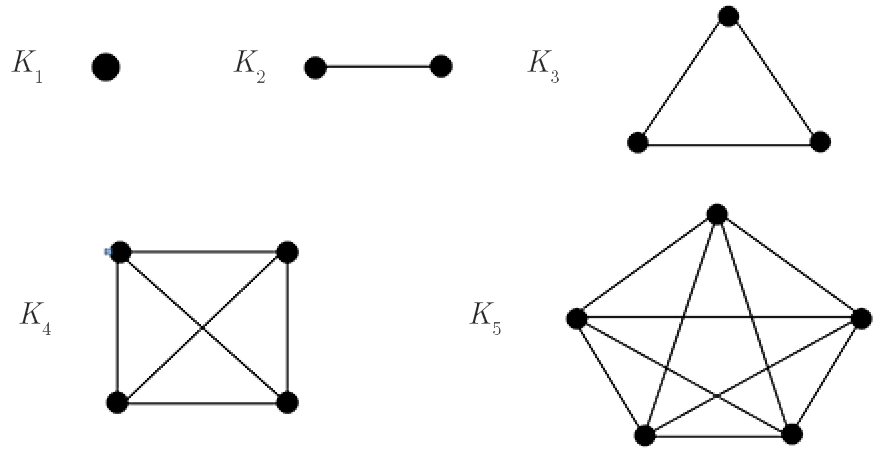
The complete graph $K_n$ is regular and each of the $n$ vertices has degree $n - 1$. Hence, the sum of the degrees is $n(n - 1)$ and by the Handshaking Lemma the number of edges in $K_n$ is, $\frac{n(n - 1)}{2}$
Exercise: Check the two properties stated above hold for the complete graphs shown.
3.3 Cycle Graph
A cycle on a graph starts at any vertex, travelling through the graph without repeating vertices or edges before ending on the start vertex. In 📷 Example 5, $BAEB$ and $AEDBA$ are both cycles while $AEDBEA$ is not a cycle as the vertex $E$ is repeated.
A cycle graph, denoted $C_n$, is a graph on $n$ vertices, $\{v_0, v_1, .\;\;\; ., v_{n-1}\}$ , with $n$ edges $\{v_0, v_1\}$, $(v_1, v_2\}$, $.\;\;\; .\;\;\; .$, $\{v_{n-1}, v_0\}$. Note that $C_n$ contains a single cycle through all the vertices.
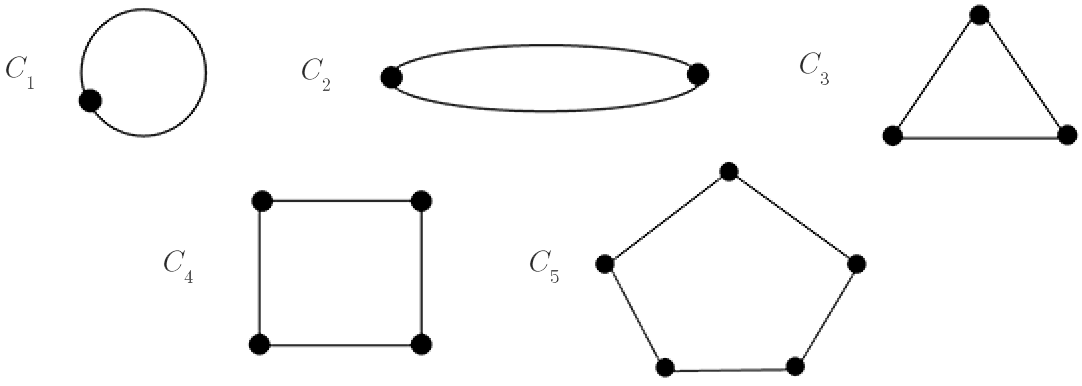
Notes
(i). In a cycle graph every vertex has degree 2.
(ii). The graph $C_1$ contains a self-loop and we shall see later that a loop contributes two to the degree of the vertex. Hence, the vertex in $C_1$ has degree 2 ensuring that the Handshaking Lemma holds.
(iii). The graph $C_2$ contains parallel edges.
A graph that contains no loops or parallel edges is called a simple graph.
3.4. Bipartite Graphs
A bipartite graph, $G(V_1, V_2)$ is a graph whose vertices can be partitioned into two disjoint subsets $V_1$ and $V_2$, where no edge joins vertices that are in the same subset. A vertex in one of the subsets may be joined to all, some, or none of the vertices in the other subset – see the diagrams below. In the case where every vertex of $V_1$ is joined to every vertex of $V_2$ then $G$ is called a complete bipartite graph and is usually denoted $K_{r, s}$ . Here $r$ and $s$ represent the number of vertices in $V_1$ and $V_2$ respectively. A bipartite graph is usually shown with the two subsets as top and bottom rows of vertices or with the two subsets as left and right columns of vertices.
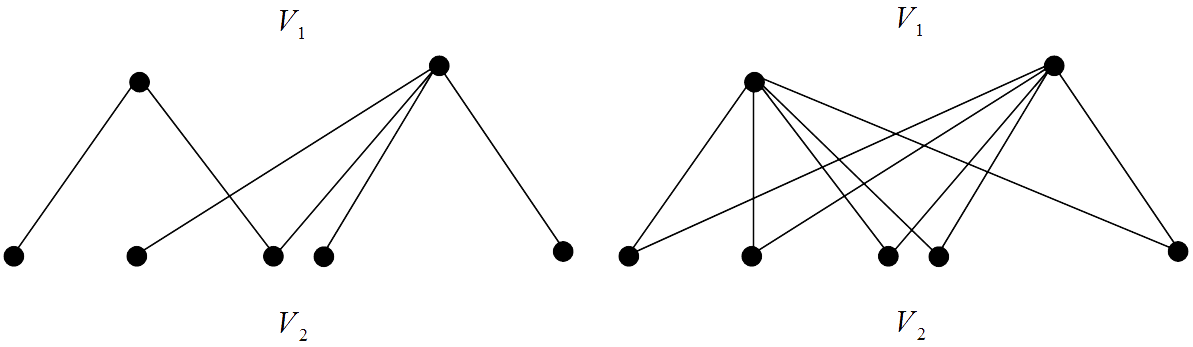
The graph on the right is the complete bipartite graph, $K_{2, 5}$ with $2 + 5 = 7$ vertices and $2 \times 5 = 10$ edges. In general, a complete bipartite graph $K_{r, s}$ has $r + s$ vertices and $r \times s$ edges.
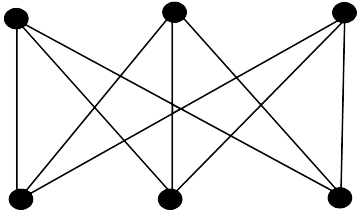
A bipartite graph $K_{r, s}$ is regular if and only if $r = s$ . The complete bipartite graph $K_{3, 3}$ shown below is regular as each vertex has degree 3.
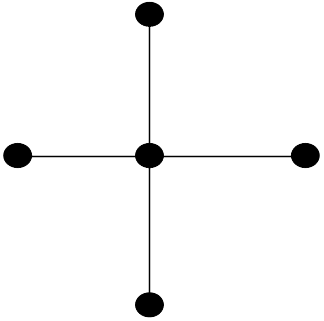
A complete bipartite graph of the form $K_{1, s}$ is called a star graph and $K_{1, 4}$ is shown below.
Example 8
The graph on the left can be drawn as a 3-regular bipartite graph by partitioning the vertices into the two sets $V_1 = \{P, R, U, W\}$, shown in red, and $V_2 = \{Q, S, T, V\}$, shown in black. Although they look different they are in fact the same graph.
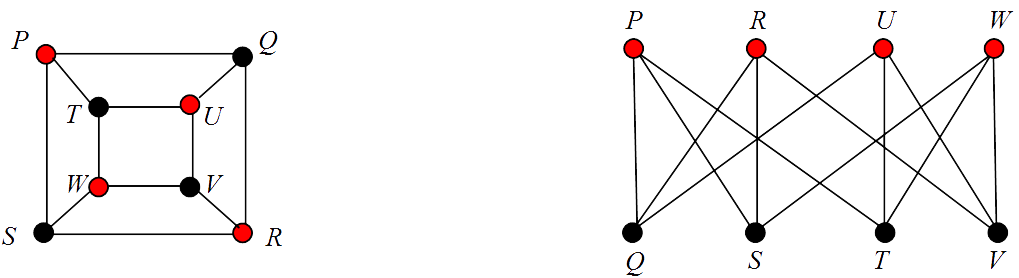
Notes
(i). Two graphs with the same number of vertices and the same number of edges, with the edges connected in the same way are said to be isomorphic.
(ii). If two graphs have different degree sequences the graphs cannot be isomorphic.
End of Example 83.5. Tree Graphs:
A forest is a graph containing no cycles and a connected forest is called a tree. Note that a graph on $n$ vertices has fewest edges when it is a tree (as it has no cycles) and most edges when it is a complete graph. Below is a forest with four components.

If the four components in the above forest are connected we obtain the tree below.

Theorem
- Let $T$ be a graph with $n > 1$ vertices. The following statements are equivalent:
- $T$ is a tree.
- $T$ is cycle-free and has $n – 1$ edges.
- $T$ is connected and has $n – 1$ edges.
- $T$ is connected and contains no cycles.
- $T$ is connected and each edge is a bridge.
- Any two vertices of $T$ are connected by exactly one path.
- $T$ contains no cycles, but the addition of any new edge creates exactly one cycle.
Note: From the above theorem it must be the case that a finite tree with $n$ vertices must have $n – 1$ edges.
3.6. Multigraphs
The diagram shows the graph $G = \{V, E\} = \{\{A, B, C, D\}, \{\{A, B\}, \{B, C\}, \{B, D\}, \{C, D\}, \{C, D\}, \{D, D\}\} \}$.

This is an example of a multigraph. A multigraph is a graph that allows the existence of loops and parallel (multiple) edges. Note that not all texts allow multigraphs to have loops and in the case when graphs include loops they are called pseudographs. We shall refer to a graph with parallel edges and/or loops as a multigraph.
A loop is an edge that links a vertex to itself. In the figure the edge $(D, D)$ is a loop and connects vertex $D$ to itself.
If two vertices are joined by more than one edge then these edges are called parallel edges. In the figure the two edges $(C, D)$ represent parallel edges.
Notes
(i). We define a loop to contribute 2 to the degree of a vertex so that the Handshaking Lemma holds for multigraphs. In the above figure vertex $D$ therefore has degree 5. The degree sum of the graph is $1 + 3 + 3 + 5 = 12$ which is twice the number of edges (6) as required by the Handshaking Lemma.
(ii). Some texts do not allow multigraphs to have loops.
X
-
4. Walks, Trails & Paths
A walk of length $k$ on a graph $G$ is an alternating sequence of vertices $( v_i )$ and edges $( e_i )$:
$v_0, e_1, v_1, e_2, v_2, e_3, \dots e_k, v_k$
where $v_i$ and $v_{i + 1}$ are both incident to $e_{i + 1}$. Note that the graph has $k + 1$ vertices and $k$ edges.
The length of a walk is the number of edges in the walk.
For convenience, and ease of reading, we omit edges and use only vertices so that the walk given above is written as $v_0, v_1, v_2, \dots ,v_{k-1}, v_k$.
Example 9
(i). A walk on the graph below is given by: $1, 5, 4, 3, 7, 1, 5, 6$ and has length $L = 7$.
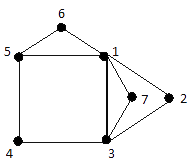
Note: A walk can repeat both edges and vertices.
(ii). A walk is said to be closed if its first and last vertices are the same, i.e. $v_0 = v_k$.
A closed walk of length 8, on the graph is given by: $1, 5, 4, 3, 7, 1, 5, 6, 1$.
(iii). A trail is a walk where all edges are distinct but vertices may be repeated.
A trail on the graph is given by: $1, 5, 4, 3, 7, 1, 6, 5$.
(iv). A closed trail is called a circuit.
A circuit on the graph is given by: $1, 2, 3, 1, 5, 4, 3, 7, 1$. Note that no edges are repeated but we are allowed to repeat vertices.
(v). A path is a trail in which all vertices are distinct. Hence, in a path neither vertices nor edges are repeated.
A path on the graph is given by: $1, 5, 4, 3, 7$.
(vi). A closed path is called a cycle.
A cycle on the graph is given by: $1, 5, 4, 3, 7, 1$. Note that no edges are repeated and the only repeated vertices are the first and last vertices.
Therefore, all trails are walks and all paths are trails.
In terms of set theory, Paths $\subseteq$ Trails $\subseteq$ Walks as shown below.
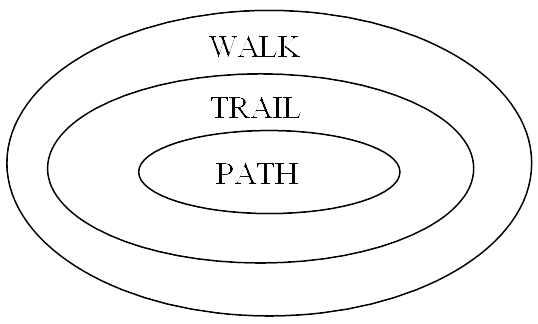
The information given above can be summarised in the following table
Repeated Vertex (Vertices) Repeated Edge(s) Open Closed Name Yes Yes Yes Open Walk Yes Yes Yes Closed Walk Yes No Yes Trail Yes No Yes Circuit (Closed Trail) No No Yes Path No No Yes Cycle (Closed Path) Adapted from, “Discrete and Combinatorial Mathematics” by R. P. Grimaldi.
Watch this video on walks, trails and paths:
End of Example 9Now that we have defined the term path we can provide an alternative definition, to that given in Section 2.2, for a graph to be connected.
A graph is connected if given any two vertices $v_i$ and $v_j$ there is a path from $v_i$ to $v_j$ .
Returning to the example in Section 2.2, reproduced below for completeness, there is clearly a path between all the vertices in the graph on the left and so it is connected. However, in the graph on the right we are unable to, for example, find a path from vertex $S$ to vertex $P$ and so the graph is disconnected.

-
5. Eulerian and Hamiltonian Graphs
This section considers special ways of traversing graphs. Examples of graph traversal problems are the Königsberg bridges and Travelling Salesman problems.
5.1. Eulerian Graphs
Definition: An Euler circuit on a graph, $G$, is a circuit (closed trail) that uses every edge of $G$ exactly once. Note that we are allowed to use the same vertex multiple times, but we can only use each edge once. A graph is Eulerian if it has an Euler circuit.
Definition: An Euler trail through a graph, $G$ is an open trail that passes exactly once through each edge of $G$. We say that $G$ is semi-Eulerian if it has an Euler trail. Note that every Eulerian graph is semi-Eulerian.
Theorem: Let $G$ be a connected graph. Then $G$ is Eulerian if and only if every vertex of $G$ has even degree.
Corollary: A connected graph is semi-Eulerian if and only if there are $0$ or $2$ vertices of odd degree. Note that if a semi-Eulerian graph has two vertices of odd degree then any Euler trail must have one of them as its initial vertex and the other as its final vertex.
The table below provides simple rules that count the number of odd degree vertices in a graph to decide whether or not it has an Euler circuit or Euler trail.
No. of Odd Vertices For a Connected Graph 0 There is at least one Euler circuit. 1 Not possible 2 No Euler circuit but at least 1 Euler trail. More than 2 No Euler circuits or Euler traits. Example 10
NON-EULERIAN
As there are four vertices of odd degree the graph is Non-Eulerian.(i). SEMI-EULERIAN
SEMI-EULERIAN
By the above corollary as there are two vertices (1 and 5) of odd degree (i.e. degree 3) the graph is semi-Eulerian.
Euler trail must start at one of the odd degree vertices and end at the other, e.g. 12342645615.(ii).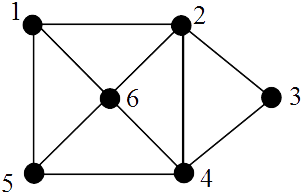 EULERIAN
EULERIAN
All vertices have even degree and so, by the above theorem, the graph is Eulerian.
Euler circuit: 1253451.(iii).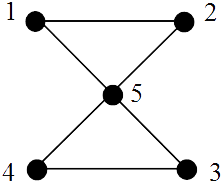
Watch this video on Euler circuits:
📹 Euler Paths and Euler Circuits
End of Example 10The following algorithm is optional but it provides a relatively simple method for finding an Euler circuit when one exists.
Fleury’s Algorithm (OPTIONAL)
If $G$ is an Eulerian graph then using the following procedure, known as Fleury’s Algorithm, it is always possible to construct an Euler circuit of $G$.
Starting at any vertex of $G$ traverse the edges of $G$ in an arbitrary manner according to the following rules:
(i). Erase edges as they are traversed and if any isolated vertices appear erase them.
(ii). At each step use a bridge only if there is no alternative.
Watch this video:
Note: Since every vertex in the Königsberg graph in 📷 Figure 2 has an odd degree it is not possible to find an Euler circuit of this graph. It is therefore impossible for someone to walk around the city in such a way that each bridge is crossed exactly once and they end up at their starting point.
5.2. Hamiltonian Graphs
Definition: A Hamiltonian cycle on a graph, $G$, is a cycle (closed path) that uses every vertex of $G$ exactly once. Note that we do not need to use all the edges. A graph is Hamiltonian if it has an Hamiltonian cycle.
Note that some texts call a Hamiltonian cycle a Hamiltonian circuit, i.e. a circuit which passes exactly once through each vertex of a graph. This definition is identical to the one above because a circuit which does not repeat vertices, apart from the starting vertex, is a cycle.
Definition: A trail that passes exactly once through each vertex of a graph $G$ and is not closed is called a Hamiltonian trail. We say that $G$ is semi-Hamiltonian. Note that every Hamiltonian graph is semi-Hamiltonian.
Note that while we have a theorem that provides necessary and sufficient conditions for a connected graph to be Eulerian (i.e. ‘$G$ is Eulerian if and only if every vertex of $G$ has even degree’) there is no similar characterisation for Hamiltonian graphs – this is one of the unsolved problems in graph theory. In general, it is much harder to find a Hamiltonian cycle than it is to find an Euler circuit.
Example 11
NON-HAMILTONIAN(i).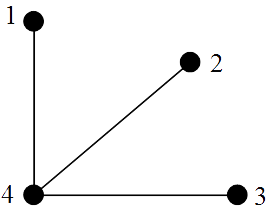 SEMI-HAMILTONIAN
SEMI-HAMILTONIAN
Hamiltonian trail: 2143.(ii).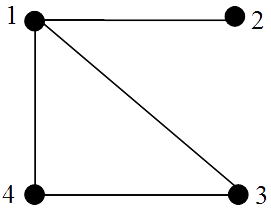 HAMILTONIAN
HAMILTONIAN
Hamiltonian cycle: 12341.
Note that we do not need to use all edges.(iii).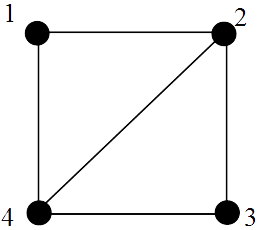
Watch this video on Hamiltonian cycles:
📹 Hamiltonian Circuits and Paths
End of Example 11Notes
(i). The Travelling Salesman problem (TSP) searches for the most efficient (least total distance) Hamiltonian cycle a salesman can take so that each of n cities is visited. To date, no solution to the TSP has been found.
(ii). An Euler circuit traverses every edge in a graph exactly once, and may repeat vertices. A Hamiltonian cycle, on the other hand, visits each vertex in a graph exactly once but does not need to use every edge.
X