10
  • 10.1
  • 10.2
  • 10.3
  • 10.4
  • Summary

  • 6. Digraphs (Directed Graphs)

    The graphs that we have met up to now have all been undirected graphs in the sense that the edges have no orientation. In this section we extend the notion of a graph to include graphs in which “edges have a direction”. These kind of graphs are known as directed graphs, or digraphs for short. As shown in the 📷 diagram the direction of an edge is defined so that movement between two vertices is only possible in the specified direction. The terminology for digraphs is essentially the same as for undirected graphs except that it is commonplace to use the term arc instead of edge. Digraphs can be used to model real-life situations such as flow in pipes, traffic on roads, route maps for airlines and hyperlinks connecting web-pages. We have actually encountered the concept of a digraph before in an earlier unit when we looked at relations on sets. In Section 3.3 of that unit we described how a relation $R$ could be represented diagrammatically by a digraph as an alternative to using an arrow diagram or a matrix.

    Watch this video on digraphs up to 1:30:

    📹 Digraphs

    Example 12

    The figure below shows a digraph on four vertices with six arcs.

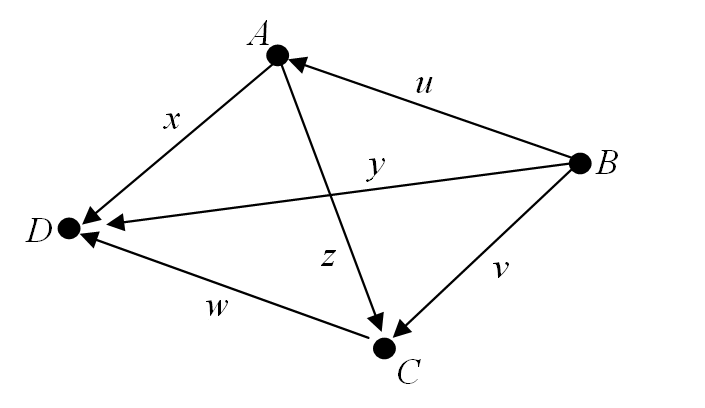
    digraph on four vertices with six arcs Diagram

    Considering the arc labelled $x$, we say that $x$ goes from $A$ to $D$ with $A$ being the initial vertex and $D$ the terminal vertex of $x$.

    End of Example 12

    6.1. In-degree and Out-degree

    The in-degree of a vertex is the number of arcs that terminate at that vertex.
    For example, the in-degree of vertex $C$ in 📷 Example 12 is 2.
    The out-degree of a vertex is the number of arcs that originate at that vertex.
    For example, the out-degree of vertex $B$ in 📷 Example 12 is 3.

    The Handshaking (Di)Lemma

    In any digraph the sum of the out-degrees, equals the sum of the in-degrees, equals the number of arcs.

    Proof: Every arc contributes exactly once to the out-degree total and exactly once to the in-degree total.

    Watch this video from 9.50 to 13.05:

    📹 Handshaking Lemma

    Note: A self-loop contributes one to the in-degree and one to the out-degree of a vertex.

    The in-degree sequence of a digraph is a bracketed list of the in-degrees of all the vertices in ascending order with repetition as necessary.

    The out-degree sequence of a digraph is a bracketed list of the out-degrees of all the vertices in ascending order with repetition as necessary.

    Example 13

    Consider the following digraph.

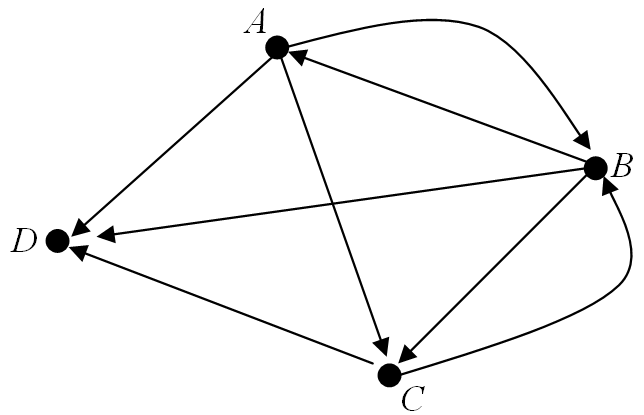
    Diagraph Diagram Example 13

    (i). Determine the in-degree and out-degree of the vertices and show that the Handshaking (Di)Lemma holds.

    (ii). Write down the in-degree and out-degree sequences.

    Solution

    (i). Create a table of in-degrees and out-degrees.

    $A$ $B$ $C$ $D$ Total
    Out-degree 3 3 2 0 8
    In-degree 1 2 2 3 8

    The sum of the out-degrees (8) equals the sum of the in-degrees (8) and these values both equal the number of edges (8). The Handshaking (Di)Lemma therefore holds.

    (ii). From the table in part (i), the in-degree sequence is, $\{ 1, 2, 2, 3 \}$ and the out-degree sequence is, $\{ 0, 2, 3, 3 \}$

    End of Example 13

    6.2. Underlying Graph

    The underlying graph of a digraph is the undirected graph obtained when the arrows are removed from the digraph.

    Example 14

    The graph underlying the digraph in 📷 Example 12 is the undirected graph shown below. Note that arcs have been replaced by edges.

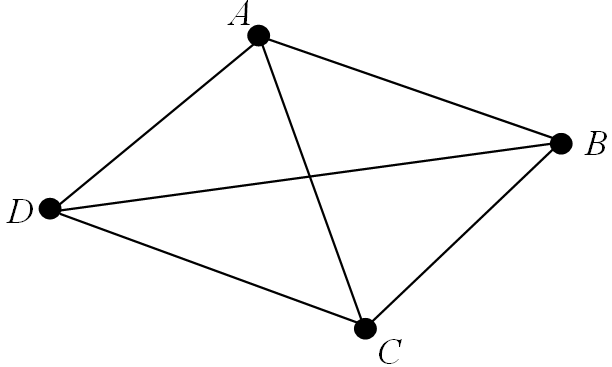    Diagraph Diagram Example 14

    End of Example 14

    6.3. Walks, Trails and Paths on Digraphs

    The concept of walks, trails and paths carries over from undirected graphs (see Section 4) to digraphs. However, we must remember that on a digraph we can only move along an edge in a single direction, i.e. the direction in which the arrow is pointing.

    Example 15

    Find a walk, trail and path on the digraph shown below.

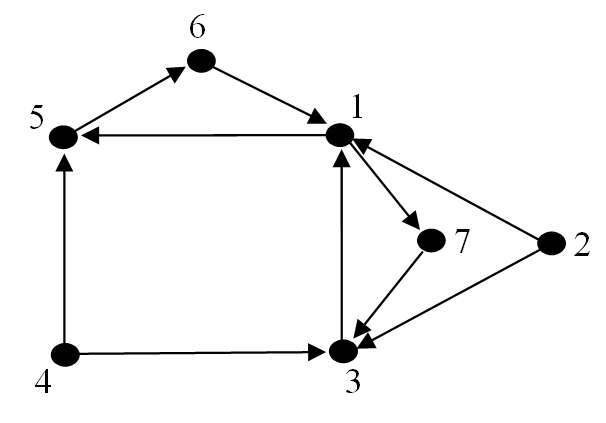
    Diagraph Diagram Example 15

    Solution

    A walk is any route from one vertex to another along the edges of the graph. A walk can repeat edges and vertices any number of times and can end on any vertex.

    One example of a walk is given by: $1, 5, 6, 1, 7, 3, 1, 5, 6$.

    A trail is a walk where all edges are distinct but vertices may be repeated.

    One example of a trail is given by: $1, 5, 6, 1, 7, 3$.

    A path is a trail in which all vertices are distinct.

    One example of a path is given by: $1, 5, 6$.

    Watch the video from 1:30 onwards:

    📹 Digraphs: Walks & Paths

    End of Example 15

    X
    digraph on four vertices with six arcs Diagram

  • 7. Adjacency and Incidence Matrices

    Up to now we have only considered graphs where the number of edges and vertices is relatively small so that they can be easily be shown in diagram form. However, as graphs become large it is no longer feasible to display them visually. When storing a graph on a computer it is useful to represent it in matrix form, as the calculation of paths, trails and circuits, for example, can easily be performed. In this section we look at two types of matrices associated with graphs; adjacency matrices and incidence matrices. We firstly present these matrices for undirected graphs before moving on to digraphs.

    7.1. Undirected Graphs and Matrices

    In Section 2 we defined an undirected graph to be a graph in which the edges have no orientation. Hence, all edges are bidirectional. For example, in the graph shown in 📷 Example 14 the edge $\{A, B\}$ is considered identical to the edge $\{B, A\}$. We now look at how to generate adjacency and incidence matrix representations for undirected graphs.

    7.1.1. Adjacency Matrix of an Undirected Graph

    If $G$ is a graph with $n$ vertices its adjacency matrix, $A$ is defined as the $n \times n$ matrix whose $ij^{th}$ entry is the number of edges joining vertex $i$ and vertex $j$.

    Watch this video up to 3:30:

    📹 Adjacency Matrix

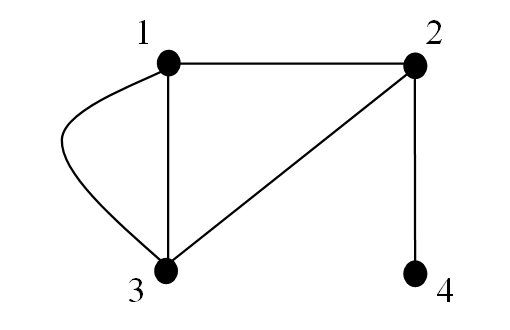
    Example 16

    Determine an adjacency matrix for following graph.

    Diagraph Diagram Example 16

    Solution

    The graph has 4 vertices and so the adjacency matrix will have dimension, $4 \times 4$. The entries of the matrix are determined as follows:
    0 edges connect vertex 1 to vertex 1, so the entry in Row1/Column1 is a ‘0’.
    1 edge connects vertex 1 to vertex 2, so the entry in Row1/Column2 is a ‘1’.
    2 edges connect vertex 1 to vertex 3, so the entry in Row1/Column3 is a ‘2’.
    0 edges connect vertex 1 to vertex 4, so the entry in Row1/Column4 is a ‘0’.

    $\matrix{1 \;\;\;\; 2 \;\;\;\, 3 \;\;\;\, 4}$

    $A = \matrix{1 \\ 2 \\ 3 \\ 4}\pmatrix{0 & 1 & 2 & 0 \\ \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot}$.

    1 edge connects vertex 2 to vertex 1, so the entry in Row2/Column1 is a ‘1’.
    0 edges connect vertex 2 to vertex 2, so the entry in Row2/Column2 is a ‘0’.
    1 edge connects vertex 2 to vertex 3, so the entry in Row2/Column3 is a ‘1’.
    1 edge connects vertex 2 to vertex 4, so the entry in Row2/Column4 is a ‘1’.

    $\matrix{1 \;\;\;\; 2 \;\;\;\, 3 \;\;\;\, 4}$

    $A = \matrix{1 \\ 2 \\ 3 \\ 4}\pmatrix{0 & 1 & 2 & 0 \\ 1 & 0 & 1 & 1 \\ \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot}$.

    2 edges connect vertex 3 to vertex 1, so the entry in Row3/Column1 is a ‘2’.
    1 edge connects vertex 3 to vertex 2, so the entry in Row3/Column2 is a ‘1’.
    0 edges connect vertex 3 to vertex 3, so the entry in Row3/Column3 is a ‘0’.
    0 edges connect vertex 3 to vertex 4, so the entry in Row3/Column4 is a ‘0’.

    $\matrix{1 \;\;\;\; 2 \;\;\;\, 3 \;\;\;\, 4}$

    $A = \matrix{1 \\ 2 \\ 3 \\ 4}\pmatrix{0 & 1 & 2 & 0 \\ 1 & 0 & 1 & 1 \\ 2 & 1 & 0 & 0 \\ \cdot & \cdot & \cdot & \cdot}$.

    0 edges connect vertex 4 to vertex 1, so the entry in Row4/Column1 is a ‘0’.
    1 edge connects vertex 4 to vertex 2, so the entry in Row4/Column2 is a ‘1’.
    0 edges connect vertex 4 to vertex 3, so the entry in Row4/Column3 is a ‘0’.
    0 edges connect vertex 4 to vertex 4, so the entry in Row4/Column4 is a ‘0’.

    $\matrix{1 \;\;\;\; 2 \;\;\;\, 3 \;\;\;\, 4}$

    $A = \matrix{1 \\ 2 \\ 3 \\ 4}\pmatrix{0 & 1 & 2 & 0 \\ 1 & 0 & 1 & 1 \\ 2 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0}$.

    This is an adjacency matrix for the 📷 graph.

    Notes

    (i). A graph can be represented by several adjacency matrices as different labelling of the vertices produces different matrices.

    (ii). In the matrix $A$, the entry $a_{ij}$ records the number of edges joining vertices $i$ and $j$.

    (iii). For an undirected simple graph: $Sum\; of\; Row\; j = Sum\; of\; Column\; j = Degree\; of\; vertex\; j$.

    (iv). The adjacency matrix for an undirected graph is symmetric, i.e. $A = A^T$.

    (v). The entries on the main diagonal are all $0$ unless the graph has loops.

    End of Example 16

    Example 17

    Given an adjacency matrix we can construct the associated graph, $G$.

    Determine the graph corresponding to the adjacency matrix below,

    $\matrix{1 \;\;\;\; 2 \;\;\;\, 3 \;\;\;\, 4}$

    $A = \matrix{1 \\ 2 \\ 3 \\ 4}\pmatrix{0 & 2 & 0 & 1 \\ 2 & 2 & 1 & 1 \\ 0 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0}$.

    Solution

    The matrix has dimension $4 \times 4$ and so the graph has 4 vertices.

    Note that a loop is defined to contribute 2 to the degree of a vertex. This approach ensures that the Handshaking Lemma holds for multigraphs.

    We proceed as follows processing one row of the matrix $A$ at a time:
    Entry in Row1/Column1 is a ‘0’so 0 edges connect vertex 1 to vertex 1.
    Entry in Row1/Column2 is a ‘2’so 2 edges connect vertex 1 to vertex 2.
    Entry in Row1/Column3 is a ‘0’so 0 edges connect vertex 1 to vertex 3.
    Entry in Row1/Column4 is a ‘1’so 1 edge connects vertex 1 to vertex 4.
    Diagraph Diagram Example 17

    Entry in Row2/Column1 is a ‘2’so 2 edges connect vertex 2 to vertex 1.
    Entry in Row2/Column2 is a ‘2’so vertex 2 has a self-loop.
    Entry in Row2/Column3 is a ‘1’so 1 edge connects vertex 2 to vertex 3.
    Entry in Row2/Column4 is a ‘1’so 1 edge connects vertex 2 to vertex 4.
    Diagraph Diagram Example 17 Figure 2

    Entry in Row3/Column1 is a ‘0’so 0 edges connect vertex 3 to vertex 1.
    Entry in Row3/Column2 is a ‘1’so 1 edge connects vertex 3 to vertex 2.
    Entry in Row3/Column3 is a ‘0’so 0 edges connect vertex 3 to vertex 3.
    Entry in Row3/Column4 is a ‘1’so 1 edge connects vertex 3 to vertex 4.
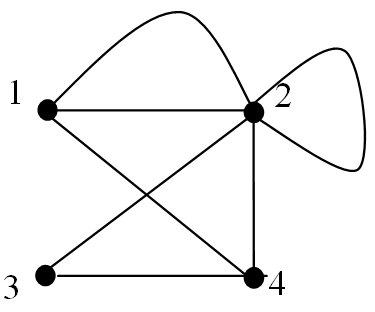
    Diagraph Diagram Example 17 Figure 3

    Entry in Row4/Column1 is a ‘1’so 1 edge connects vertex 4 to vertex 1.
    Entry in Row4/Column2 is a ‘1’so 1 edge connects vertex 4 to vertex 2.
    Entry in Row4/Column3 is a ‘1’so 1 edge connects vertex 4 to vertex 3.
    Entry in Row4/Column4 is a ‘0’so 0 edges connect vertex 4 to vertex 4.

    Diagraph Diagram Example 17 Figure 3

    This is the graph that corresponds to the given adjacency matrix.

    End of Example 17

    7.1.2. Incidence Matrix of an Undirected Graph

    The incidence matrix for a graph, $G$, with $n$ vertices and m edges is the $n \times m$ matrix $M$ where

    $\cases {1\; \text{if vertex}\; i\; \text{is incident to edge}\; j\; \\ 0 \;\text{otherwise}} $

    Each row in an incidence matrix corresponds to a vertex and each column corresponds to an edge. Hence, if $e_k$ is an edge joining vertices $i$ and $j$ then all the elements in column $k$ are $0$ except for $m_{i k}$ and $m_{j k}$ which both equal 1.

    Watch the video from 5:25 onwards:

    📹 Incidence Matrix

    Example 18

    Determine an incidence matrix for the graph shown below.

    Diagraph Diagram Example 18

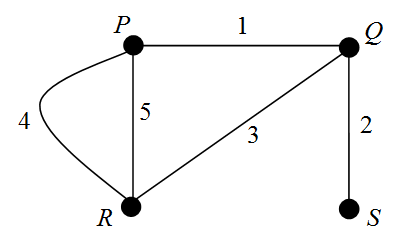
    Solution

    The graph has $4$ vertices and $5$ edges and so the incidence matrix will have dimension, $4 \times 5$. Label the rows of the matrix $P, Q, R$ and $S$ and the columns $1, 2, 3, 4$ and $5$.

    $\matrix{1 \;\; 2 \;\;\; 3 \;\;\; 4\;\;\; 5}$

    $M = \matrix{P \\ Q \\ R \\ S}\pmatrix{\cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot}$.

    Consider the edges of the graph (columns of the matrix) in turn and assign a “$1$” or a “$0$” respectively, to the relevant location in the matrix depending on whether or not the edge is incident on the associated vertex.

    Column 1: Edge $1$ is incident on vertices $P$ and $Q$ so enter a “$1$” in the corresponding rows.

    The remaining entries in Column $1$ are all set to $0$.

    $\matrix{1 \;\;\, 2 \;\;\; 3 \;\;\; 4\;\;\; 5}$

    $M = \matrix{P \\ Q \\ R \\ S}\pmatrix{1 & \cdot & \cdot & \cdot & \cdot \\ 1 & \cdot & \cdot & \cdot & \cdot \\ 0 & \cdot & \cdot & \cdot & \cdot \\ 0 & \cdot & \cdot & \cdot & \cdot}$.

    Column 2: Edge $2$ is incident on vertices $Q$ and $S$ so enter a “$1$” in the corresponding rows.

    The remaining entries in Column $2$ are all set to $0$.

    $\matrix{1 \;\;\;\, 2 \;\;\; 3 \;\;\; 4\;\;\; 5}$

    $M = \matrix{P \\ Q \\ R \\ S}\pmatrix{1 & 0 & \cdot & \cdot & \cdot \\ 1 & 1 & \cdot & \cdot & \cdot \\ 0 & 0 & \cdot & \cdot & \cdot \\ 0 & 1 & \cdot & \cdot & \cdot}$.

    Column 3: Edge $3$ is incident on vertices $Q$ and $R$ so enter a “$1$” in the corresponding rows.

    The remaining entries in Column $3$ are all set to $0$.

    $\matrix{1 \;\;\;\, 2 \;\;\;\, 3 \;\;\; 4\;\;\; 5}$

    $M = \matrix{P \\ Q \\ R \\ S}\pmatrix{1 & 0 & 0 & \cdot & \cdot \\ 1 & 1 & 1 & \cdot & \cdot \\ 0 & 0 & 1 & \cdot & \cdot \\ 0 & 1 & 0 & \cdot & \cdot}$.

    Column 4: Edge $4$ is incident on vertices $P$ and $R$ so enter a “$1$” in the corresponding rows.

    The remaining entries in Column $4$ are all set to $0$.

    $\matrix{1 \;\;\;\, 2 \;\;\;\, 3 \;\;\;\, 4\;\;\; 5}$

    $M = \matrix{P \\ Q \\ R \\ S}\pmatrix{1 & 0 & 0 & 1 & \cdot \\ 1 & 1 & 1 & 0 & \cdot \\ 0 & 0 & 1 & 1 & \cdot \\ 0 & 1 & 0 & 0 & \cdot}$.

    Column 5: Edge $5$ is incident on vertices $P$ and $R$ so enter a “$1$” in the corresponding rows.

    The remaining entries in Column $5$ are all set to $0$.

    From the above an incidence matrix for the graph is therefore:

    $\matrix{1 \;\;\;\, 2 \;\;\;\, 3 \;\;\;\, 4\;\;\;\; 5}$

    $M = \matrix{P \\ Q \\ R \\ S}\pmatrix{1 & 0 & 0 & 1 & 1 \\ 1 & 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 & 1 \\ 0 & 1 & 0 & 0 & 0}$.

    Alternative Approach

    Some people prefer to concentrate on vertices when constructing the incidence matrix and look at the edges incident on a specific vertex. The matrix is therefore constructed one row at a time

    Row 1: Vertex $P$ is incident on edges $1, 4$ and $5$ so enter a “$1$” in all relevant

    locations in Row 1. The remaining entries in Row $1$ are all $0$.

    Row 2: Vertex $Q$ is incident on edges $1, 2$ and $3$ so enter a “$1$” in all relevant

    locations in Row 2. The remaining entries in Row $2$ are all $0$.

    Row 3: Vertex $R$ is incident on edges $3, 4$ and $5$ so enter a “$1$” in all relevant

    locations in Row 3. The remaining entries in Row $3$ are all $0$.

    Row 4: Vertex $S$ is only incident on edge $2$ so enter a “$1$” in the relevant location in

    Row 4. The remaining entries in Row $4$ are all $0$.

    We obtain the same incidence matrix as with the previous method,

    $\matrix{1 \;\;\;\, 2 \;\;\;\, 3 \;\;\;\, 4\;\;\;\; 5}$

    $A = \matrix{P \\ Q \\ R \\ S}\pmatrix{1 & 0 & 0 & 1 & 1 \\ 1 & 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 & 1 \\ 0 & 1 & 0 & 0 & 0}$.

    Notes

    (i). As was the case for adjacency matrices a graph can be represented by several incidence matrices as different labelling of the vertices produces different matrices.

    (ii). As every edge is incident on exactly two vertices (no loops) each column of $M$ contains exactly two $1$’s and so all column sums all equal $2$.

    (iii). Each row sum gives the degree of the corresponding vertex, e.g. vertex $P$ has degree $3$, and the corresponding row of $M$, i.e. the first row of $M$, has row sum $3$

    (iv). Parallel edges in a graph produce identical columns in the incidence matrix.

    (v). A row containing all $0$’s indicates an isolated vertex.

    End of Example 18

    We previously demonstrated how, given an adjacency matrix we can construct the corresponding graph. In a similar manner we can derive a graph from its incidence matrix.

    Example 19

    Determine the graph corresponding to the incidence matrix below.

    $\matrix{1 \;\;\;\, 2 \;\;\;\, 3 \;\;\;\, 4\;\;\;\; 5}$

    $M = \matrix{P \\ Q \\ R \\ S}\pmatrix{1 & 0 & 0 & 1 & 1 \\ 0 & 0 & 1 & 1 & 1 \\ 0 & 1 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 & 0}$.

    Solution

    The matrix has dimension $4 \times 5$ and so the graph has $4$ vertices and $5$ edges.

    We proceed as follows processing one column of the matrix $M$ at a time:

    Column 1: Edge $1$ is incident on vertices $P$ and $S$ so join these two vertices.

    Column 2: Edge $2$ is incident on vertices $R$ and $S$ so join these two vertices.

    Column 3: Edge $3$ is incident on vertices $Q$ and $S$ so join these two vertices.

    Column 4: Edge $4$ is incident on vertices $P$ and $Q$ so join these two vertices.

    Column 5: Edge $5$ is incident on vertices $P$ and $Q$ so join these two vertices.

    Applying the above we obtain the graph below:

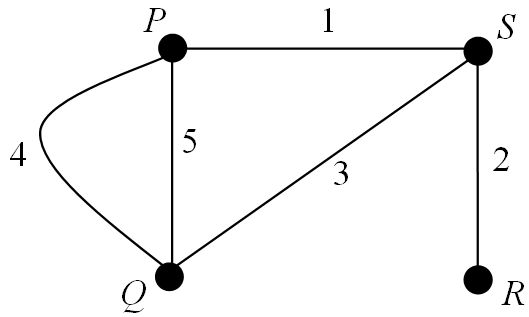
    Diagraph Diagram Example 19

    A point to note here is that this is actually the same graph as in 📷 Example 18 except that the vertices have been labelled differently. As noted above the different labelling leads to a different incidence matrix.

    End of Example 19

    7.2. Digraphs and Matrices

    In this section we look at how to generate adjacency and incidence matrices for digraphs.

    7.2.1. Adjacency Matrix of a Digraph

    The adjacency matrix of a digraph having $n$ vertices is a $n \times n$ matrix. For each directed edge $\{v_i, v_j\}$, i.e. arrow from vertex $v_i$ to vertex $v_j$, we place a ‘$1$’ at the $i^{th}$ row, $j^{th}$ column position. Otherwise we place a ‘$0$’ at the appropriate position in the matrix.

    Watch this video

    📹 ADJACENCY MATRIX OF A DIGRAPH

    Example 20

    Determine an adjacency matrix for the digraph shown below,

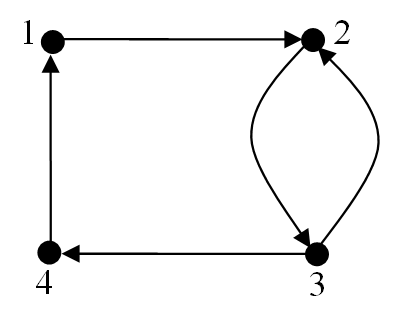
    Diagraph Diagram Example 20

    Solution

    The digraph has $4$ vertices and so the adjacency matrix will have dimension $4 \times 4$.
    There is an arc from vertex $1$ to vertex $2$, so the entry in Row1/Column2 is a ‘$1$’
    There is an arc from vertex $2$ to vertex $3$, so the entry in Row2/Column3 is a ‘$1$’
    There is an arc from vertex $3$ to vertex $2$, so the entry in Row3/Column2 is a ‘$1$’
    There is an arc from vertex $3$ to vertex $4$, so the entry in Row3/Column4 is a ‘$1$’
    There is an arc from vertex $4$ to vertex $1$, so the entry in Row4/Column1 is a ‘$1$’
    All other entries in the adjacency matrix will be zero

    From the calculations above an adjacency matrix for the digraph is therefore:

    $\matrix{1 \;\;\;\; 2 \;\;\;\, 3 \;\;\;\, 4}$

    $A = \matrix{1 \\ 2 \\ 3 \\ 4}\pmatrix{0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 1 & 0 & 0 & 0}$.

    End of Example 20

    Notes

    The total number of $1$’s in an adjacency matrix equals the number of arcs in the digraph.

    In general, the adjacency matrix is not symmetric for a digraph.

    The number of $1$’s in row $i$ of an adjacency matrix corresponds to the out-degree of vertex $i$.

    The number of $1$’s in column $j$ of an adjacency matrix corresponds to the in-degree of vertex $j$.

    7.2.2. Incidence Matrix of a Digraph - (OPTIONAL)

    The incidence matrix for a digraph with $n$ vertices and $m$ arcs is an $n \times m$ matrix where each row corresponds to a vertex and each column corresponds to an arc.

    If an arc originates at vertex $i$ and terminates at vertex $j$ then the column corresponding to that arc will contain a "$- 1$" in row $i$ and a “$1$" in row $j$ with all other entries in the column being $0$.

    Watch this video:

    📹 INCIDENCE MATRIX OF A DIGRAPH

    Example 21

    Find the incidence matrix for the following digraph.

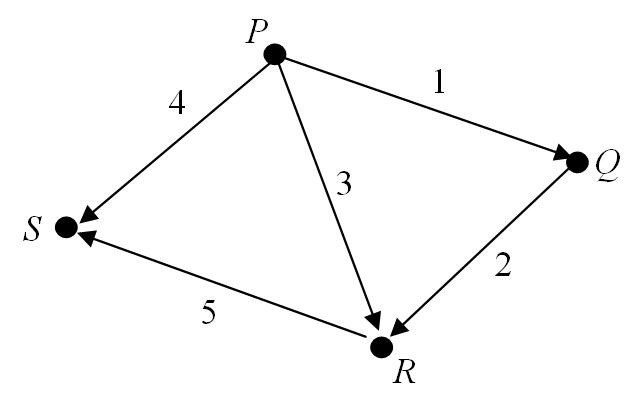
    Diagraph Diagram Example 21

    Solution

    The graph has $4$ vertices and $5$ arcs and so the incidence matrix will have dimension, $4 \times 5$. Label the rows of the matrix $P, Q, R$ and $S$ and the columns $1, 2, 3, 4$ and $5$.

    Consider the arcs of the graph (columns of the matrix) in turn.

    Column 1: Arc 1 originates at vertex $P$ and terminates at vertex $Q$, so enter a “ $-1$ ” in the row for $P$ and a “$1$" in the row for $Q$.

    The remaining entries in Column $1$ are all set to $0$.

    $\matrix{\;\;\;\;1 \;\;\; 2 \;\;\; 3 \;\;\; 4\;\;\, 5}$

    $M = \matrix{P \\ Q \\ R \\ S}\pmatrix{-1 & \cdot & \cdot & \cdot & \cdot \\ \;\;\;1 & \cdot & \cdot & \cdot & \cdot \\ \;\;\;0 & \cdot & \cdot & \cdot & \cdot \\ \;\;\;0 & \cdot & \cdot & \cdot & \cdot}$.

    Column 2: Arc $2$ originates at vertex $Q$ and terminates at vertex $R$, so enter a “ $-1$ ” in the row for $Q$ and a "$14$" in the row for $R$.

    The remaining entries in Column $2$ are all set to $0$.

    $\matrix{\;\;\;\;1 \;\;\;\;\;\;\, 2 \;\;\; 3 \;\;\; 4\;\;\, 5}$

    $M = \matrix{P \\ Q \\ R \\ S}\pmatrix{-1 & \;\;\;0 & \cdot & \cdot & \cdot \\ \;\;\;1 & -1 & \cdot & \cdot & \cdot \\ \;\;\;0 & \;\;\;1 & \cdot & \cdot & \cdot \\ \;\;\;0 & \;\;\;0 & \cdot & \cdot & \cdot}$.

    We continue in this way to obtain the following incidence matrix for the digraph.

    $\matrix{\;\;\;\;1 \;\;\;\;\;\;\, 2 \;\;\;\;\;\;\, 3 \;\;\;\;\;\;\, 4\;\;\;\;\;\;\, 5}$

    $M = \matrix{P \\ Q \\ R \\ S}\pmatrix{-1 & \;\;\;0 & -1 & -1 & \;\;\;0 \\ \;\;\;1 & -1 & \;\;\;0 & \;\;\;0 & \;\;\;0 \\ \;\;\;0 & \;\;\;1 & \;\;\;1 & \;\;\;0 & -1 \\ \;\;\;0 & \;\;\;0 & \;\;\;0 & \;\;\;1 & \;\;\;1}$.

    Note that the column sum for each column will always be $0$. Can you explain why?

    End of Example 21

    7.3. Eulerian Digraphs

    A digraph is Eulerian if it is connected and the in-degree of each vertex equals its out-degree.

    Equivalently a digraph is Eulerian if it is connected and there exists a closed trail (circuit) which uses each arc exactly once. Vertices however, can be repeated. This definition is essentially the same as for undirected graphs, see Section 5.1, except that we can only traverse the graph in the direction of the arrows.

    Watch this video:

    📹 Eulerian Digraphs

    Example 22

    Consider the following digraph, $D$.

    Diagraph Diagram Example 22

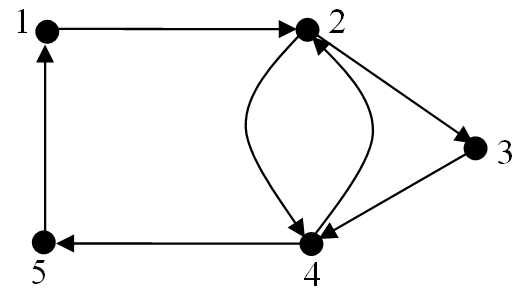
    (i). Determine an adjacency matrix for $D$.

    (ii). Is $D$ Eulerian? Either state an Euler circuit or explain why $D$ is not Eulerian.

    Solution

    (i). The digraph has $5$ vertices and so the adjacency matrix will have dimension $5 \times 5$ .

    There is an arc from vertex $1$ to vertex $2$, so the entry in Row1/Column1 is a ‘$1$’
    There is an arc from vertex $2$ to vertex $3$, so the entry in Row2/Column3 is a ‘$1$’
    There is an arc from vertex $2$ to vertex $4$, , so the entry in Row2/Column4 is a ‘$1$’
    There is an arc from vertex $3$ to vertex $4$, , so the entry in Row3/Column4 is a ‘$1$’
    There is an arc from vertex $4$ to vertex $2$, , so the entry in Row4/Column2 is a ‘$1$’
    There is an arc from vertex $4$ to vertex $5$, so the entry in Row4/Column5 is a ‘$1$’
    There is an arc from vertex $5$ to vertex $1$, so the entry in Row5/Column1 is a ‘$1$’
    All other entries in the adjacency matrix will be zero.

    The adjacency matrix is therefore,

    $\matrix{1 \;\;\;\, 2 \;\;\;\, 3 \;\;\;\, 4\;\;\;\, 5}$

    $A = \matrix{1 \\ 2 \\ 3 \\ 4 \\ 5}\pmatrix{0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 0}$.

    (ii). Recall that the row sums of $A$ give the out-degrees while the column sums provide the in-degrees of the vertices. We construct the following table:

    Vertex Out-Degree In-Degree
    1 1 1
    2 2 2
    3 1 1
    4 2 2
    5 1 1

    This digraph is Eulerian as the out-degree of each vertex is the same as its in-degree.

    An Euler circuit is given by: $1, 2, 3, 4, 2, 4, 5, 1$.

    End of Example 22

    7.4. Hamiltonian Digraphs

    For a digraph, $D$, to be Hamiltonian it must be connected and include a cycle (closed path) that uses every vertex of $D$ exactly once. Such a cycle is called a Hamiltonian cycle and need not use every arc of the graph.

    Example 23

    A Hamiltonian cycle for the digraph in 📷 Example 22 is, $1, 2, 3, 4, 5, 1$. We have been able to visit each vertex exactly once and return to the start vertex.

    End of Example 23

    X
    Diagraph Diagram Example 14
    X
    Diagraph Diagram Example 14
    X
    Diagraph Diagram Example 18 Figure 2
    X
    Diagraph Diagram Example 22 Figure 2

  • 8. Adjacency Matrices & Paths

    Adjacency matrices can be used to determine the number of paths of different lengths between vertices.

    In an adjacency matrix the entry at position $(i, j)$ corresponds to the number of paths of length $1$ between vertex $v_i$ and vertex $v_j$. It is also possible to construct matrices that provide information on paths of length other than $1$ between vertices.

    For example, to calculate the matrix for paths of length $2$ we must square the matrix $A$, i.e. calculate $A^2 = A \times A$.

    In general, if we calculate $k^{th}$ power of the adjacency matrix $A$ the entry at position $(i, j)$ of the matrix $A^k$ indicates the number of paths of length $k$ between vertex $v_i$ and vertex $v_j$ .

    Now watch this video on path matrices:

    📹 Path matrices

    Example 24

    Let $D$ be a digraph with $5$ vertices as shown:

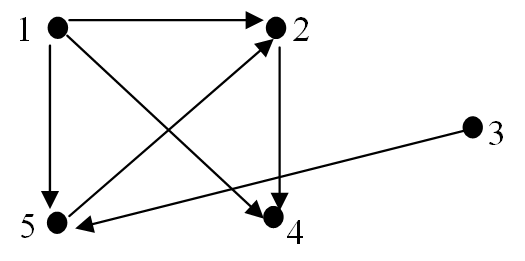
    Diagraph Diagram Example 23

    An adjacency matrix for $D$ is given by

    $\matrix{1 \;\;\; 2 \;\;\;\, 3 \;\;\; 4\;\;\;\, 5}$

    $A = \matrix{1 \\ 2 \\ 3 \\ 4 \\ 5}\pmatrix{0 & 1 & 0 & 1 & 1 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0}$.

    If a path of length $1$ exists between two vertices (i.e. vertices are adjacent) then there is a $1$ in the corresponding position in the adjacency matrix, $A$. Here, for example, inspection of $A$ reveals the following paths of length $1$:
    from vertex $1$ to vertices $2, 4$ and $5$
    from vertex $2$ to vertex $4$
    from vertex $3$ to vertex $5$
    from vertex $5$ to vertex $2$.

    There are no paths of length $1$ from vertex $4$ to any of the other vertices.

    To calculate paths of length $2$ the adjacency matrix, $A$, is multiplied by itself to give $A^2$ , i.e.

    $\matrix{\;1 \;\;\; 2 \;\;\;\, 3 \;\;\;\, 4\;\;\;\, 5}$

    $A^2 = \matrix{1 \\ 2 \\ 3 \\ 4 \\ 5}\pmatrix{0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0}$.

    The matrix shows that there are only four paths of length $2$ in the digraph:
    from vertex $1$ to vertex $2$,
    from vertex $1$ to vertex $4$,
    from vertex $3$ to vertex $2$
    from vertex $5$ to vertex $4$.

    In general, the matrix of path length $k$ is generated by multiplying the matrix of path length $k -1$ by the matrix of path length $1$, i.e. the adjacency matrix, $A$.

    We say that a digraph is strongly connected if there is a path from every vertex to every other vertex.

    End of Example 24

  • 9. Other Graphs

    This section briefly looks at two other common types of graphs used to represent different scenarios, weighted graphs and tournament graphs.

    9.1. Weighted Graphs (OPTIONAL)

    The edges in a graph can be weighted or unweighted. In a weighted graph a non-negative real number is assigned to each edge, $e$, and is called the weight of $e$, denoted $w(e)$. These weights may correspond to the lengths of roads (edges) between towns (vertices) in a graphical representation of a map and we may be required to find the length of the shortest path from town $A$ to town $L$, say. The problem is then to find the path from $A$ to $L$ with minimum weight.

    An example of a shortest path problem is the well-known Travelling Salesman Problem.

    Now watch this video on weighted graphs:

    📹 Weighted graphs

    Example 25

    The shortest path from $A$ to $L$ has length 17 and is shown in bold in the figure.

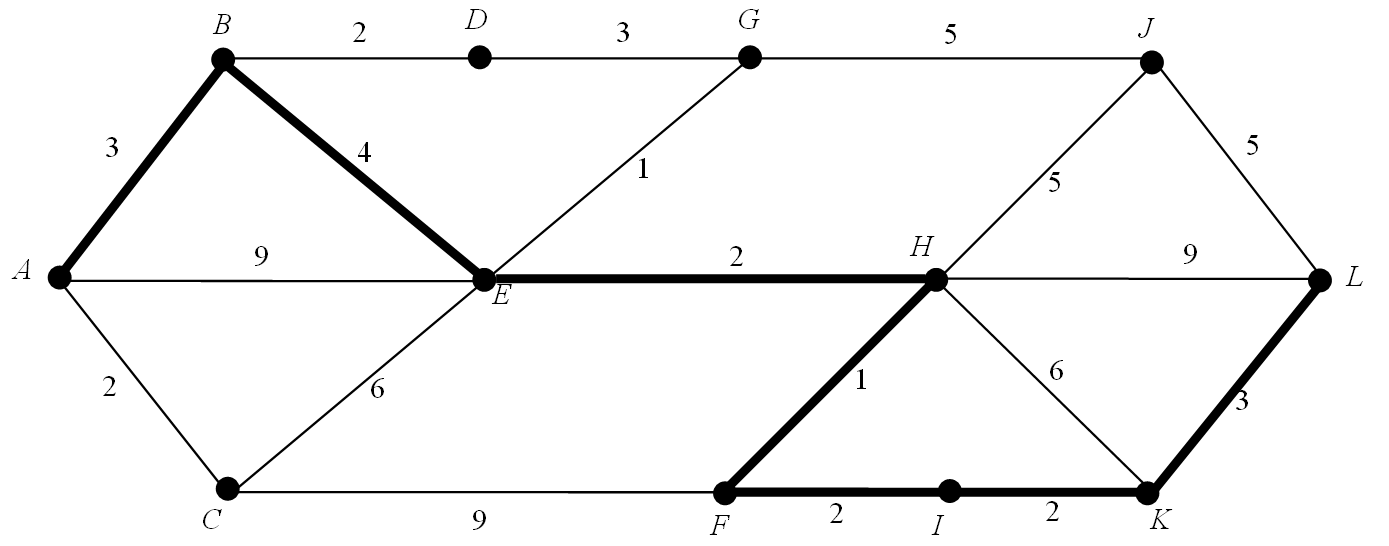
    Shortest Path Diagram
    (from Introduction to Graph Theory, Fourth Edition, Wilson R.J., 1996)

    End of Example 25

    9.1.1. Adjacency Matrix of a Weighted Graph

    The adjacency matrix is calculated in the same way as for the previous examples except that instead of placing a $1$ in the $i^{th}$ row and $j^{th}$ column when vertices $v_i$ and $v_j$ are adjacent we enter the weight.

    Example 26

    $A = \pmatrix{0 & 6 & 0 & 0 & 7 \\ 6 & 0 & 2 & 3 & 0 \\ 0 & 2 & 0 & 4 & 0 \\ 0 & 3 & 4 & 0 & 6 \\ 7 & 6 & 0 & 6 & 0}$.

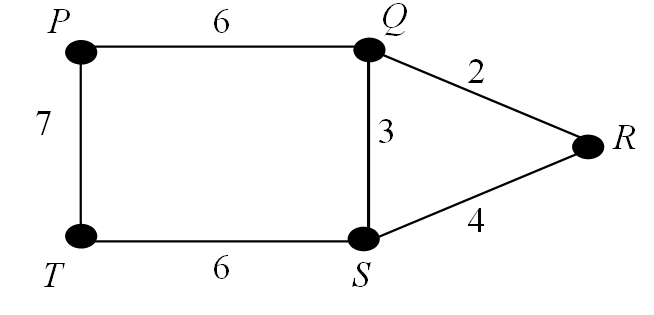    Diagraph Diagram Example 26

    End of Example 26

    9.2. Tournament Graphs – (OPTIONAL)

    A tournament is a digraph whose underlying graph ( the graph obtained from the digraph by removing the arrows ) is a complete graph. Tournaments can be used to record pairwise preferences between the objects in a set, or the results of games in a round-robin tournament ( a competition in which every team plays every other team ).

    Now watch this video:

    📹 Tournament graphs

    Example 27

    Suppose that in some round-robin tournament there are four competitors: $A, B, C$ and $D$. The results of head-to-head matches are as follows:
    $A$ beats $B$ and $D$, but loses to $C$.
    $B$ beats $C$ and $D$,
    $C$ loses to $D$.

    This set of results can be represented using the following tournament graph where an arc in the graph such as $\{ A, B \}$ indicates that team $A$ beat team $B$:

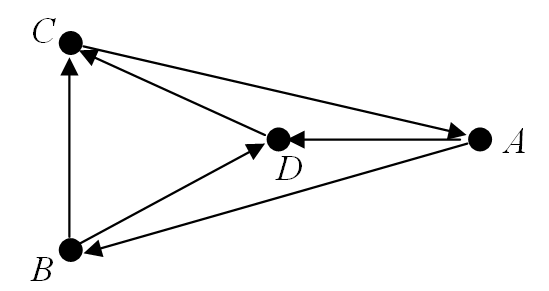
    Diagraph Diagram Example 26

    Note that ranking the contestants using these results is impossible, since $A$ beat $B, B$ beat $D, D$ beat $C$, but $C$ beat $A$!

    If a ranking (not necessarily unique or ‘fair’) is required from any tournament then the vertices along a Hamiltonian path (a path between two vertices that visits each vertex exactly once) in the tournament will give rise to one. In the above example $ABDC$ is a ranking and so is $DCAB$.

    End of Example 27

    Example 28

    A market research organisation asked 10 individuals to test drive two cars each from a possible 5 and report a preference between the two. The results of the tests were recorded as shown in the following table where a 1 indicates that the car in the row was preferred to the car in the column.

    Chagwar Gentley Horsche BMX Saudi
    Chagwar 1 1 1
    Gentley 1 1 1
    Horsche 1 1
    BMX
    Saudi 1 1

    (i). Sketch the tournament graph associated with the data in the table.

    (ii). Construct a ranking for these cars based on the results of the pairwise tests.

    Solution

    (i). The figure below shows the tournament graph.

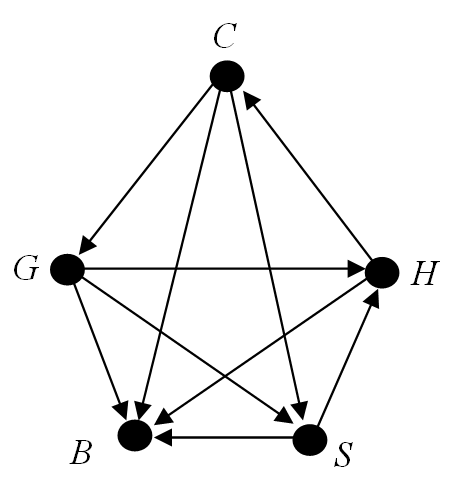
    Diagraph Diagram Example 28

    Possible ranking: Chagwar, Gentley, Saudi, Horsche, BMX.

    Note that this ranking corresponds to the Hamiltonian path, CGSHB.

    End of Example 28

  • Summary

    This unit has provided an introduction to the important topic of graph theory and you should now be able to:
    identify different types of general graphs including: undirected and directed graphs; simple graphs and multigraphs.
    understand basic terminology associated with graphs, including: connected, vertices, edges, arcs, adjacent, incident, degree sequence, in-degree, out-degree, etc.
    identify different types of specific graphs: regular graphs, complete graphs, cycle graphs, bipartite graphs, tree graphs, weighted graphs and tournament graphs.
    state the Handshaking Lemmas for both undirected graphs and digraphs.
    identify walks trails and paths on undirected graphs and digraphs.
    determine whether or not a graph (undirected or digraph) is Eulerian and identify an Euler circuit if one exists.
    determine whether or not a graph (undirected or digraph) is Hamiltonian and, for “small” graphs, identify a Hamiltonian cycle if one exists.
    construct adjacency and incidence matrices for undirected graphs and digraphs.
    construct the corresponding undirected graph or digraph from an adjacency or incidence matrix.

    The next section extends the topic of trees, introduced in Section 3.5, to briefly investigate the role of a tree as a data structure and its applications in computer science.

School of Computing, Engineering and Built Environment