Overview

The basic layout of a symmetric cryptosystem: (note that the ciphertext is sometimes called the cryptogram)

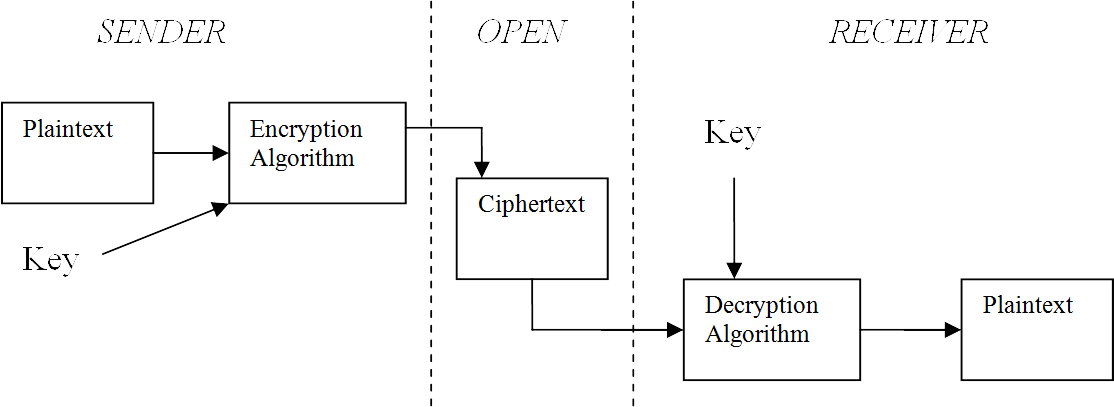
The encryption and decryption processes are composed of two parts: the algorithm and the key. In modern systems the algorithms are implemented on computers. The region between the dotted lines entitled ‘Open’ implies that anyone has access to the ciphertext. The assumption being that only the transmitter and receiver of the message have access outside of the delimited region.

We consider an encryption algorithm as a family of $1-1$ functions from the set of all possible messages $M$ to the set of all possible ciphers $C$. The individual encryption functions are identified by their key $–$ an element of the set $K$. Formally an encryption function is $E_k:M \rightarrow C $ for some $k \in K$ .

Corresponding to each encryption function there is a decryption function: $D_{k'}:M \rightarrow C$ satisfying $D_{k'}\; oE_k = id$ (equivalently $D_{k'}(E_k(m)) = m$ for all possible $m \in M$.

The process of creating the ciphertext from the plaintext is called encipherment and of changing ciphertext back into plaintext is called decipherment.

Any person (or machine) in the open that is listening to the ciphertext transmissions is called an Eavesdropper or Interceptor. If the eavesdropper is trying to obtain the plaintext they are said to be attacking the system and if they succeed in obtaining the key that goes with the algorithm they are said to have broken or cracked the system.

The study of these systems is called cryptology and this is broken down into cryptography (the design of cryptographic systems) and cryptanalysis (the investigation of attacks on systems).

Keys

Secrecy is in the Key

Encryption procedures are represented by algorithms operating on the plaintext. The algorithm incorporates a key as part of the encipherment process. The same algorithm can be used with different keys, making for robust security.

It is always assumed that an attacker knows the algorithm in use and that the security is entirely in the keys (this is referred to as Kerckhoffs’ principle). If a system is dependent on the secrecy of the algorithm; then anyone involved in using/designing/implementing the algorithm is a point of weakness (an ex-employee for example). Once the operation of such an algorithm is exposed then not only are all future texts potentially compromised (unless system immediately changed, which requires operators to know the break in security has taken place) but all previous ciphertexts are definitely compromised!

Given that the security of the cryptosystem is in the key, it must be arranged so that it is hard to find the key by a trial and error approach (a brute force attack). A good cryptosystem allows for a very large number of keys.

We distinguish between two types of cryptosystem based on how the encipherment and decipherment keys are related.

Symmetric Cryptography

For symmetric systems the key is considered to be the ‘same’ for both the encryption and decryption processes $–$ this is not literally true; the understanding is that the keys are so closely related that knowledge of one implies knowledge of the other. For example when we discussed the Caeser cipher the encipherment key was a shift by $n$ which implied the decipherment key was a shift by $–n$.

Asymmetric Cryptography

In contrast, asymmetric cryptography uses two keys, which while related, are such that knowledge of the encipherment key does not give knowledge of the decipherment key. For asymmetric systems the keys are different but clearly they need to be related in some way for the system to work: but it is the case that the relationship between the two keys makes it simply too difficult to determine one from the other.

Throughout this section we use the following simplified alphabet.

$A = \{a, b, c, \ldots, z, \Delta \}$

The last symbol has been introduced to represent a space.

Note that there are many other possible choices of alphabet: it does not have to be the Latin one (ie $a,b,\ldots,z$); it might include punctuation, capitals, numbers; it might be entirely made up of on non-standard symbols.

Mono-alphabetic Substitution Cipher

A monoalphabetic substitution cipher involves the substitution of each letter in an alphabet by a different letter in the alphabet (or one from a different alphabet). The decipherment involves replacing the substituted letter with its original value.

The simplest example of a monoalphabetic substitution cipher is the Ceasar cipher already described and briefly reviewed here, using the functional notation which has now been introduced.

Caeser Cipher Review

Identify each letter with its integer equivalent: $\Delta=0, a=1, b=2,\ldots,z = 26$. (For simplicity we ignore punctuation and spaces.). The key for the cipher is a number in the range $1$ to $26 –$ we denote this number by $n$. Note that we do not use $0$ as an allowable key. The replacement of the alphabet with the numbers $\{0,\ldots,26\}$ is equivalent to replacing the alphabet $A$ by $\mathbb{Z}_{27}$ .

To encipher we use the transformation (function):

$E_n : \mathbb{Z}_{27} \rightarrow \mathbb{Z}_{27}$

$x \alpha (x + n)(Mod\; 27)$

Example: Using $E_3$

TEXT:	b	e	w	a	r	e	$\Delta$	t	h	e	$\Delta$	i	d	e	s	$\Delta$	o	f	$\Delta$	m	a	r	c	h
NUMERICAL:	2	5	23	1	18	5	0	20	8	5	0	9	4	5	19	0	15	6	0	13	1	18	3	8
CRYPTOGRAM:	5	8	26	4	21	8	3	23	11	8	3	12	7	8	22	3	18	9	3	16	4	21	6	11

To decipher the cryptogram we use the inverse function:

$D_n : \mathbb{Z}_{27} \rightarrow \mathbb{Z}_{27}$

$x\, \alpha\, (x-n)(Mod \; 27)$

We can easily verify that this decrypts $E_n$ since

$D_n(E_n(x)) = (x + n) - n (MOD \;27) = x$

EXAMPLE (Continued) (recall subtraction mod 3 can also be done by adding 24 modulo 27)

CRYPTOGRAM:	5	8	26	4	21	8	3	23	11	8	3	12	7	8	22	3	18	9	3	16	4	21	6	11
DECRYPTION:	2	5	23	1	18	5	0	20	8	5	0	9	4	5	19	0	15	6	0	13	1	18	3	8
TEXT:	b	e	w	a	r	e	$\Delta$	t	h	e	$\Delta$	i	d	e	s	$\Delta$	o	f	$\Delta$	m	a	r	c	h

For a full mathematical description that takes the letters and produces the ciphertext, define the function.

$T_A : A \rightarrow \mathbb{Z}_{27} \\\;\;\;\;\;\;\; \Delta\, \alpha\;\;\;\;\;\; 0 \\\;\;\;\;\;\;\;\; a \; \alpha \;\;\;\;\;\; 1 \\ \;\;\;\;\;\;\;\; b \; \alpha \;\;\;\;\;\; 2 \\ \;\;\;\;\;\;\;\;\;\; M \;\;\;\; M \\ \;\;\;\;\;\;\;\; z \; \alpha \;\;\;\;\, 26$

The Ceasar encryption becomes $E_n \;oT_A$ and the decryption process can be represented as $T_A^{-1} oD_n$.

Because of the limited key space, breaking this code is trivial. There are only 26 keys, and a basic attack would involve trying each key in turn until sensible plaintext is obtained.

General Mono-alphabetic Substitution ciphers

A monoalphabetic substitution (MS) cipher implies that each letter in the alphabet is replaced by a single symbol (usually – but not necessarily- from the same alphabet).

For an alphabet with 27 symbols (mapped onto itself) there are (27 factorial less 1) different permutations of the symbols; any one (apart from the do nothing permutation) could form a cipher. Actually, it would not make sense to use just any – we would want to avoid permutations that leave lots of letters fixed; but this still leaves a ‘very’ large number of keys.

EXAMPLE

We usually want a simple key that is easy to remember. To determine an arbitrary permutation we might use a key word (or phrase) as follows.

Suppose that the key word is PERMUTATION. Delete any multiple copies of letters appearing in the key word or phrase to get PERMUTAION (we removed second T). Now construct a cipher table as follows:

Plain

$\Delta$

a

b

c

d

e

f

g

h

I

j

k

l

m

n

o

p

q

r

S

t

u

v

w

x

y

z

Cipher

P

E

R

M

U

T

A

I

O

N

B

C

D

F

G

H

J

K

L

Q

S

V

W

X

Y

Z

$\Delta$

Another variant is to make the key be composed of a key word and a number. The number indicates the placement of the keyword in the table. So if the keyword is as in the last example, and the keynumber is 7, then the encryption table is:

Plain

$\Delta$

a

b

c

d

e

f

g

h

i

j

k

l

m

n

o

p

q

r

S

t

u

v

w

x

y

z

Cipher

S

V

W

X

Y

Z

$\Delta$

P

E

R

M

U

T

A

I

O

N

B

C

D

F

G

H

J

K

L

Q

The student should not lose sight of the fact that the key is simply a device for generating a permutation – one that can easily be remembered.

Cracking the Mono-alphabetic Substitution Cipher

We will have more to say on code breaking later but it is useful to introduce some basic ideas in this lecture.

Recall that we always assume that the algorithm implementing the cipher is known and that the only defence against attack is the secrecy of the key (Kerkhoffs’ principle).

We have introduced one of the simplest mono-alphabetic substitution (MS) ciphers (The Caeser) and indicated that a brute force attack was effective (i.e. try all possible keys). For the more general MS cipher the brute force case is impractical: there are potentially trillions upon trillions of keys.

On the other hand a known plaintext attack is easy. In a known plaintext attack we have a copy of some plaintext and the corresponding ciphertext. It should be clear that a reasonable quantity of material can be used to immediately generate a look-up table. (Even a small amount of known plaintext enciphered will generate most of the table.)

The more likely situation (for this type of code) is that we would have to carry out a ciphertext only attack (ie we only have the ciphertext).

The English (or any other language) has a known frequency of occurrence of each letter; this frequency pattern will be repeated in the ciphertext allowing us to pair up letter’s using the fact that they will have approximately the same frequency in both plaintext and ciphertext!

This procedure can be augmented by exploiting repetition and structure in English (or other language’s) words.

The susceptibility of MS to frequency analysis attacks makes them weak. The next evolution of ciphers involves using substitutions that hide the frequency of letters. The most effective approach is the polyalphabetic substitution ciphers (eg Vigenere), which we will discuss later.

Other approaches include treating letters as pairs (bigrams) and substituting for these (for example the Playfair cipher – see later) - this flattens the frequency distribution but it is still prone to a frequency attack when there is sufficient ciphertext to exhibit the distribution of bigrams. The idea can be extended to trigrams etc these ciphers are harder to break but they can still be attacked using frequency analysis. Yet another approach is Homophonic substitution ciphers

Homophonic substitution ciphers

In these ciphers the plaintext alphabet is mapped into a larger ciphertext alphabet. This allows more than one symbol to be associated with a plaintext symbol. In particular common letters such as e can be replaced by one of several options. (See Q3 in the tutorial.)

Polyalphabetic Cipher

The most famous attempt to break up the frequency profile of the underlying plaintext language is the Viginére (pronounced visionair) Cipher. This cipher uses more than one Caesar substitution cipher. The system is called polyalphabetic since is uses more than one copy of the alphabet for the substitutions.

EXAMPLE

To construct a cipher with key proper. Consider the plain text message

‘salt and viginére’

Look up the first letter (s) in the row along the top and move down the column until opposite the first letter of the key (p) and read the entry ‘H’. Next plaintext ($a$) and next key letter (r) gives cipher ‘R’. Next plaintext (l) and next key letter (o) gives cipher ‘Z’. Continuing to the end of the key we get: HRZIEE.

To continue encoding we continue with the text but restart at the beginning of the key.

The next plaintext letter is d and the restarted key is (p) ; look down column d and along row p to get ‘S’. The ciphertext is now HRZIEES. Continue to get the full ciphetext:

HRZIEESMWVMETIS

Note that the first occurrence in the plaintext of the letter e is enciphered as R and the second as E. This observation is important, as it demonstrates how the frequency analysis attack will break down. This led people to believe that the code, with reasonably long keys, was unbreakable (Not so).

To decipher a Vigenére ciphertext reverse the encipherment process.

EXAMPLE

Decipher the Viginére cipher: UOOOTKQQKFWVKSX, with the key dog.

Move to row d and scan along to find entry U the plain text is in the column header.; ie r. Move to row o read along to find entry O, the column had is ‘a’.
Continue to obtain ‘railfencecipher’ or ‘rail fence cipher’.

The mathematical presentation of the cipher, acting on the $\mathbb{Z}_{27}$ , with a key of length $r$, is

$E_{(k_1,K_2, \ldots, k_r)}(m_i) = c_i = (M_i + k_{i(MOD\,r)})(MOD \, 27)$

Where $m_i$ is the $i$th letter of the message,.

The decipherment

$D_k(c_i) = (c_i - k_{i(MOD\,r)})(MOD\,27) = m_i$