-
Sorting Algorithms
- Earlier on we looked at two sorting algorithms:
- Bubble sort
- Insertion sort
From that earlier work, we concluded that in the worst case scenario (numbers sorted in reverse order) that the complexity function
$$f(n) = \frac{n(n-1)}{2} = \frac{n^2}{2} - \frac{n}{2} $$
In each case, as $n$ becomes larger, the asymmetric behaviour of $f(n)$ is such that ${\Large\frac{n}{2}}$ can be dropped as $n^2/2$ is significantly larger than ${\Large\frac{n}{2}}$.
in big $\text{O}$ notation, both of these sort algorithms are $\text{O}(n^2)$.
- Lets now have a look at two more sorting algorithms Namely,
- Radix sort
- Shell sort
-
Radix sort
At first glance this seems to be an unusual sorting method. There are no comparisons and no swaps with other numbers in the list. Instead, numbers are taken one by one, looked at, and depending on the value of a digit in a particular column ( units, tens, hundreds, etc ) the number is placed into a particular bucket.
At the end of each pass, the numbers are retrieved from the buckets in a particular way:
start at the bucket with the smallest number and work your way along the buckets until you have no more buckets.
take the number out of each bucket in the first in and first out order.
For example, suppose we have three buckets
0 1 2 420 131 292 271 872 652 Then, the new order is: $420,\; 131,\; 271,\; 292,$ etc.
At the end of each pass, the numbers are retrieved from the buckets and placed out in order.
In the next pass, the process is repeated for the digits in the next column.
If each number has $k$ digits, then this entire process is repeated k times. Once each digit in the numbers has been looked at, then in the last pass, the numbers are retrieved out of the buckets and the numbers are sorted into order!
About the method
The method is particularly useful when the numbers (or text) all have the same fixed number of digits.
When we look at an example of the radix sort, we will insert blank spaces in front of smaller numbers and interpret these blanks as zeros. So for numbers with three digits.

the number $5$ is interpreted as $005$.
Least Significant Digit Radix Sort
In the least significant digit radix sort, we start at the least significant digit and work towards the most significant digit.
For example:

Example of Radix Sort
We will use the radix sort method to sort the following six numbers:
$47, 204, 4, 92, 891, 198$
As we are dealing with numbers, we will use ten buckets (radix of 10). If we were using upper case characters, we would use twenty six buckets (radix of $26$).
Let’s start with the number $47$. Treat it as though it had three digits.

We will need ten buckets. These are numbered from $0$ to $9$.
First Pass
As the right most digit in the number $47$ is $7$, this number is put into bucket $7$.
Bucket No. 0 1 2 3 4 5 6 7 8 9 891 092 204 047 198 004 Next, the number $204$ is put into bucket $4$. Continue in this way until all the numbers are in buckets.
Now take the numbers out in the order from left to right and from top tobottom. The numbers are now ordered as:
$891, 092, 204, 004, 047, 198$
Pass 2
Now the process is repeated starting with the number $891$. As this is the second pass, we look at the second digit from the right. It is number $9$. Hence, the number $891$ is put into bucket number $9$.
Bucket No. 0 1 2 3 4 5 6 7 8 9 204 047 891 004 092 198 The number $092$ is also put into bucket $9$ because the second digit from the right is a $9$, etc.
Reading the numbers in the order left to right and from top to bottom gives:
$204, 004, 047, 891, 092, 198$
Pass 3
Now repeat the process starting with the number $204$. As the third digit from the right is the number $2$, the number $204$ goes into bucket number $2$.
Bucket No. 0 1 2 3 4 5 6 7 8 9 004 198 204 891 047 092 The number $004$ goes into bucket $0$ because the third digit from the right is the number $0$. Continue in this way until all the numbers are in a bucket.
Reading the numbers from the buckets gives the order:
$004, 047, 093, 198, 204, 891$
You will notice that the numbers are now sorted into ascending order.
Efficiency of Radix Sort
- Let’s assume that we have a little routine that allows us to identify any digit at any significant place in a number. During each pass each number has
- a digit identified
- a write to a bucket
- a read from a bucket
In our example, there
Pass Identity Digit Write Read 1 6 6 6 2 6 6 6 3 6 6 6 18 18 18 If we assume for the moment that the three operations of “Identify, write and read” takes one timetick, then the first pass takes $6$ timeticks, the second pass takes $6$ timeticks and the third pass takes $6$ timeticks. Hence, for three digits numbers, we require $(3)(6) = 18$ timeticks.
If we had n numbers, each with the $k$ digits, the the number of timeticks would be $n k$. Hence, the complexity function $f(n) = nk$. This is a linear function.
For example,
Number of numbers $n$ Number of digits $k$ Total number of timeticks $nk$ 1000 5
10
1005,000
10,000
100,00010,000 5
10
10050,000
100,000
1,000,000Comparing these, as the number of numbers increases from 1,000 to 10,000 (10 times more) the number of timeticks (identify digit, write, read) increases by 10 times.
This is a linear complexity function $f(n) = nk$. This is a fast sort compared to the insertion sort or the bubble sort. Hence, it is more efficient than the insertion sort or the bubble sort.
As $f(n) = nk$, then big $\text{O}$ is $\text{O}(n)$ for the radix sort.
Dealing with Positive and Negative Numbers
We can devise different mechanisms to deal with this.
For example, the list can be split as follows:
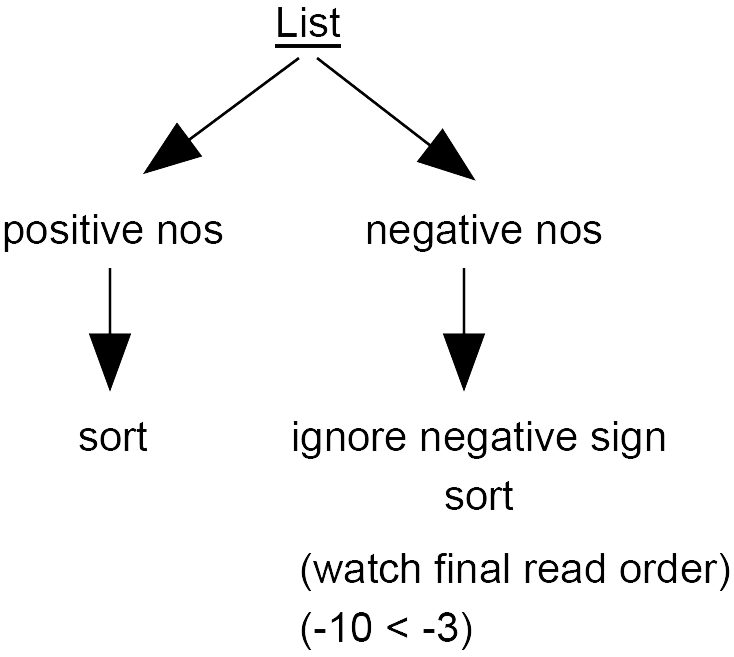
Or, instead of having 10 buckets we have 20 buckets; 10 for positive numbers and 10 for negative numbers.
Duplicate Numbers
If it is important, in the case of duplicate numbers, this least significant radix sort will preserve the original order of duplicate keys. On the other hand, a radix sort based on the most significant digit does not.
Example
When telephone numbers all have the same number of digits, the radix system is a good choice of algorithm

- Sorting n numbers requires:
- 11 passes
- on each pass identify digit, write; and read
Hence $f(n) = (11)(n) = 11n$
End of ExampleExample
let’s assume that the maximum number of letters in a word list is seven. Text such as “AS” and “Assert” can be rewritten as:
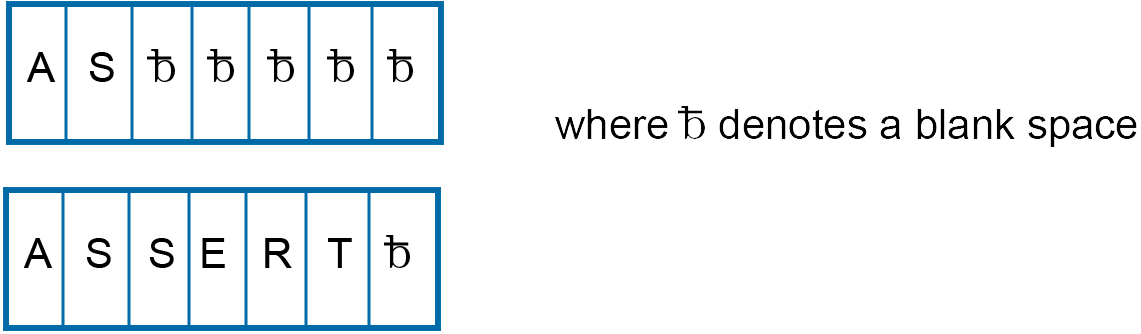
Now all the words can be treated as though they had seven characters (letters).
Here, for upper case letters we would need $26 + 1 = 27$ buckets. The blank bucket would be required to be on the right most position.

Here $f(n) = 7n$.
End of Example -
Shell Sort
The Shell sort was devised by Donald Shell in 1959. The method uses a mixture of bubble sort ideas and insertion sort ideas.
To start with comparisons and swaps are not made between adjacent numbers. Instead a distance gap is devised and then far away objects are compared and if necesary swapped.
Then the distance gap is halved and so closer objects are compared and if necessary swapped.
As each pass of the object list is made, the distance gap continues to be halved until on the final pass adjacent objects in the list are compared and swapped. This last pass is similar in idea to the insertion sort.
There are many variations of the Shell sort and the efficiency of the algorithm is determined by the distance gap selection.
Shell Sort - Elementary Variation
let’s keep the same numbers that were used in both the insertion sort and in the bubble sort.
Here, there were six numbers, so set $n = 6$. The gap distance (or slider) is set initially as:
$k = \text{int} \Big(n\Big/2\Big) = \text{int} \Big(6\Big/2\Big) = 3$
A slider starts at the first number and goes to the fourth number.
Pass 1
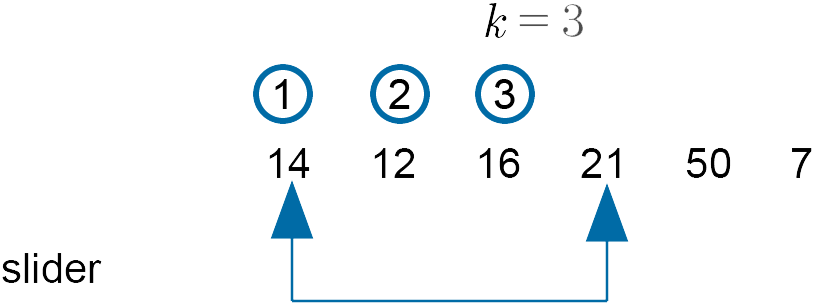
Now compare 14 and 21 - do not swap
Move slide up one.

Now compare 12 and 50 - do not swap
Move the slider up one.
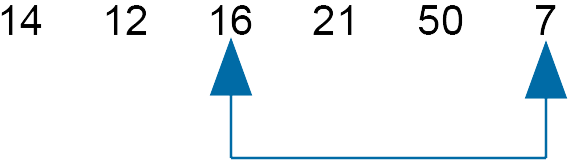
Compare 16 and 7 - swap
$14 \;\;\; 12 \;\;\; 7 \;\;\; 21 \;\;\; 50 \;\;\; 16$
As the slider cannot go up any further then this is the end of the first pass.
Pass 2
set $k := \text{int} (\text{add value of}\; k/2)$
$= \text{int}\Big(3\Big/2\Big)= 1$
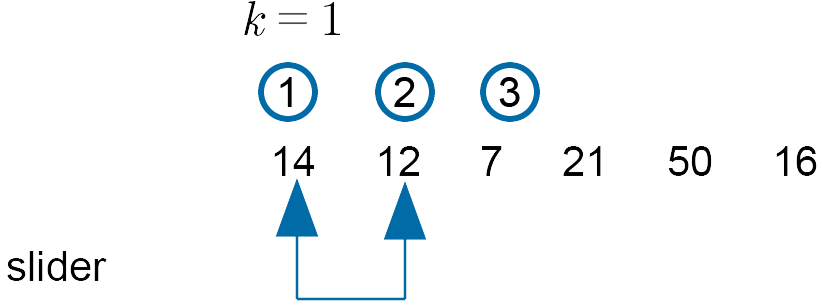
Compare 14 and 12 - swap
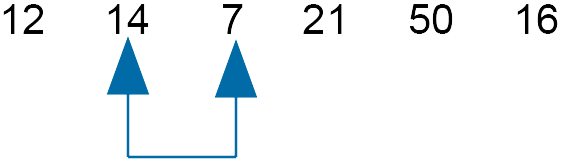
Although we have swapped, the slider cannot move down as we are at the bottom of the list. So move the slider up.
Compare 14 and 7 - swap
The order is now
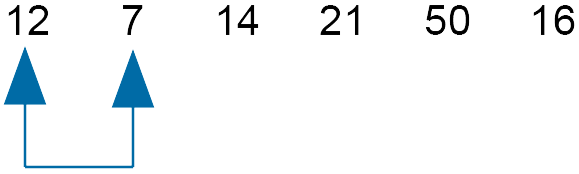
As we swapped numbers, move the slider down and compare 12 and 7 - swap order.
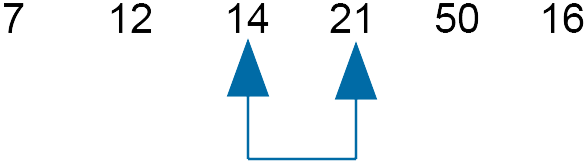
Although we have swapped 12 and 7, the slider cannot be moved down. Instead the slider moves back and we compare 14 and 21 - do not swap.
Move the slider along one.
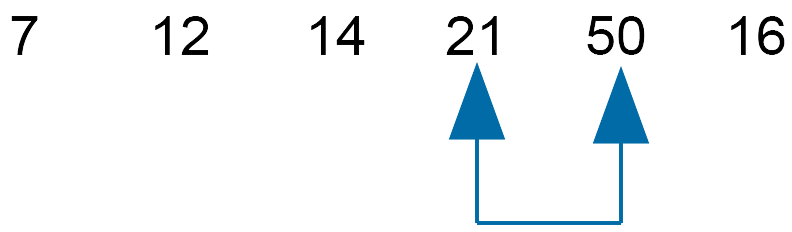
Compare 21 and 50 - do not swap.
Move the slider along one.

Compare 50 and 16 - swap
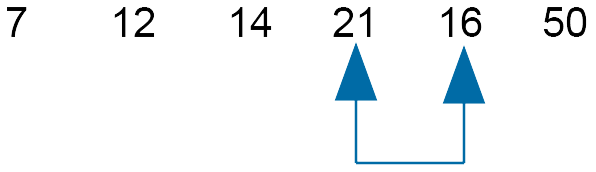
As a swap between 50 and 16 was made, move the slider down one.
Compare 21 and 16 - swap
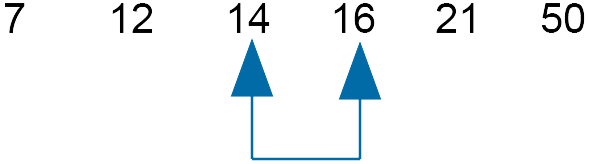
As a swap between 21 and 16 was made move the slider down one.
Compare 14 and 16 - do not swap
As we have reached the top of the list there are no more numbers to consider ( and $k = 1$ ). Hence we have reached the end of the algorithm and the numbers are now sorted smallest to largest.
Comparison and Swap Count
A count of the comparisons and swaps gives:
No. of Comparisons No of swaps Pass 1 3 1 Pass 2 8 5 11 6 For these numbers in their starting order the insertion sort did 9 comparions and 6 swaps.
The bubble sort did 15 comparisons and 6 swaps
Looking at the three sets of results, there is not much to distinguish between them.
Worst case scenario
Suppose the initial set of numbers were in reverse order.
$50 \;\;\; 21 \;\;\; 16 \;\;\; 14 \;\;\; 12 \;\;\; 7$
How many comparisons and swaps are required?
Set $k = \text{int}\Big(6\Big/2\Big) = \text{int}(3) = 3$
Pass 1
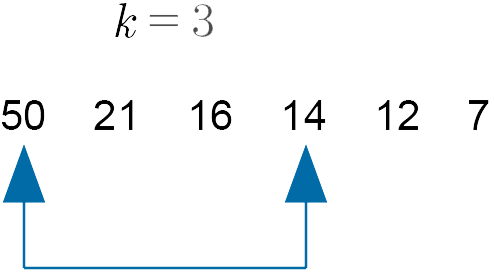
Compare 50 and 14 - swap
Move slider along

Comparing 21 and 12 - swap
Move slider along
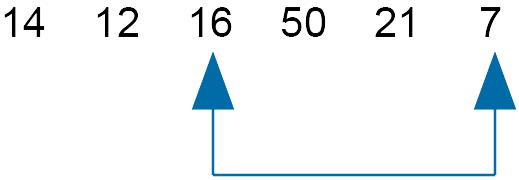
Compare 16 and 7 - swap
$14 \;\;\; 12 \;\;\; 7 \;\;\; 50 \;\;\; 21 \;\;\; 16$
This is the end of the first pass.
Pass 2
$k : = \text{int}$
$= \text{int}\Big(3\Big/2\Big) = 1$
$= \text{int}(1.5) = 1$
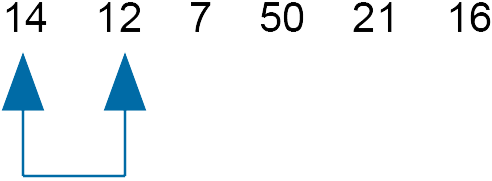
Compare 14 and 12 - swap
move slide along one
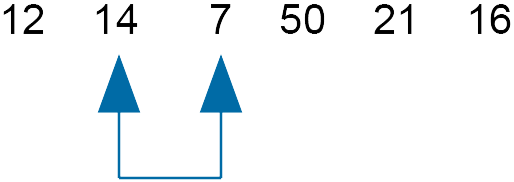
Compare 14 and 7 - swap
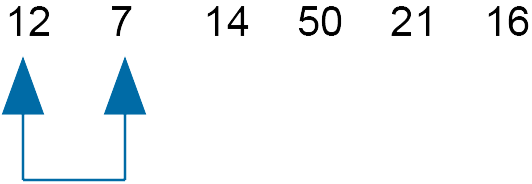
As a swap was made, move the slider back one.
Compare 12 and 7 - swap
As the slider cannot move down any further, it returns to compare the next two numbers.
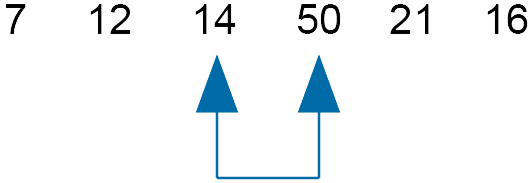
Compare 14 and 50 - do not swap
Move slider along one.
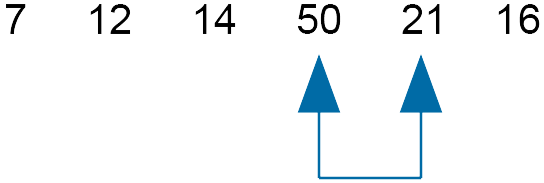
Compare 50 and 21 - swap
As there has been a swap, move the slider back one
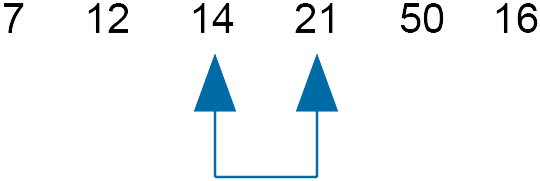
Compare 14 and 21 - do not swap
Return the slider to its previous position and move up one.

Compare 50 and 16 - swap
As we have swapped, move the slider down one.
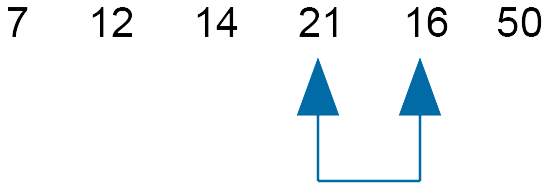
Compare 21 and 16 - swap
Move slider down one.
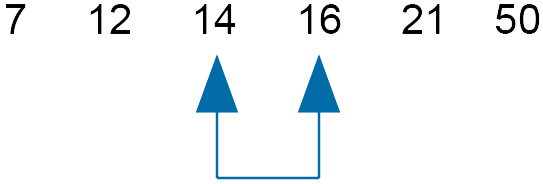
Compare 14 and 16 - do not swap
The slider cannot move back to its previous position plus one, because it has reached the end of the list.
The list is now sorted from lowest to highest number.
Comparison
A count of the number of comparisons and swaps gives.
No. of Comparisons No of swaps Pass 1 3 3 Pass 2 9 5 12 9 Insertion 15 15 Bubble 15 15 Comparing the three algorithms for comparisons and swaps, although there is not much in it, the shell sort looks a little bit better.
Big O
Both the insertion sort and the bubble sort are $\text{O}(n^2)$.
Our version of the shell Sort would give a $\text{O}( n\, log\, n)$.
Other versions of the Shell Sort wiould give a different big $\text{O}$.
-
Encryption
If we have some plaintext file and we want to make the data more secure, then the data may be encrypted. This way, if the file is lost, copied or stolen, then it is more difficult for the data to be understood.
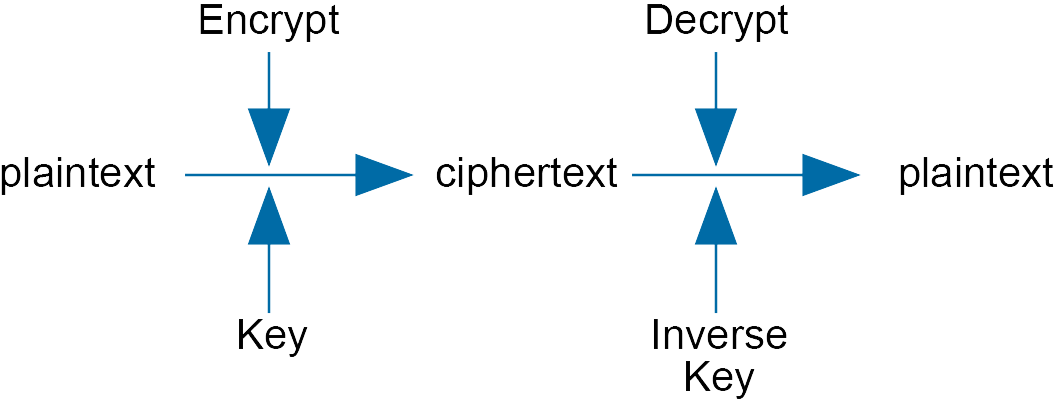
The encryption process can be illustrated as:
Basic Cipher Terminology
plaintext - The original text file that can be understood by anyone.
ciphertext - The string of symbols produced by a cipher. The meaning is unintelligible.
encryption - The process of transforming plaintext into ciphertext by a cipher.
key - The parameter associated with encryption. This key can be changed to give different ciphertext from the same plaintext.
decryption - The process of transforming ciphertext to plaintext using knowledge of the key.
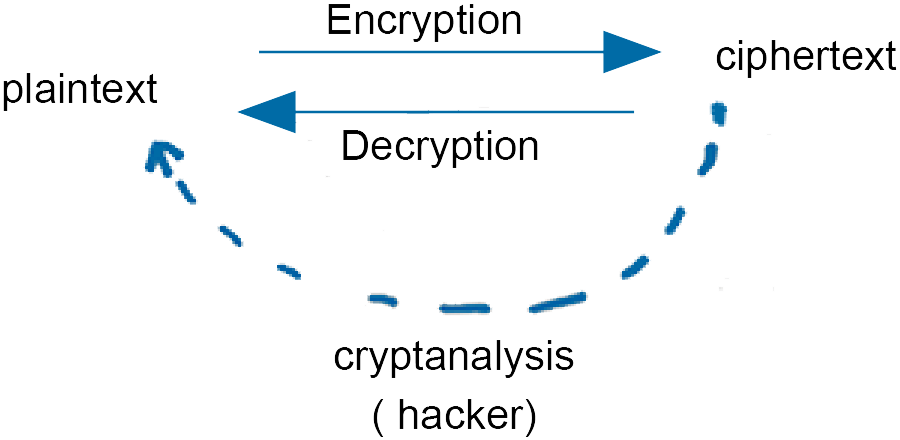
cryptanalysis - The attempt to convert ciphertext to plaintext using knowledge of the key.
cryptosystem - The complete cipher system; all plaintext, all keys, all ciphertexts and the transformation processes
Cipher Processes
- Three separate processes have been identified
- Encryption
- Decryption
- Cryptanalysis
More About Ciphers
- With mathematical encryption, all ciphers involve
- substitution of text
- transposition of text
- or a mixture of both
From a mathematical viewpoint, the entities in the study of ciphers are:
Symbolically, this is
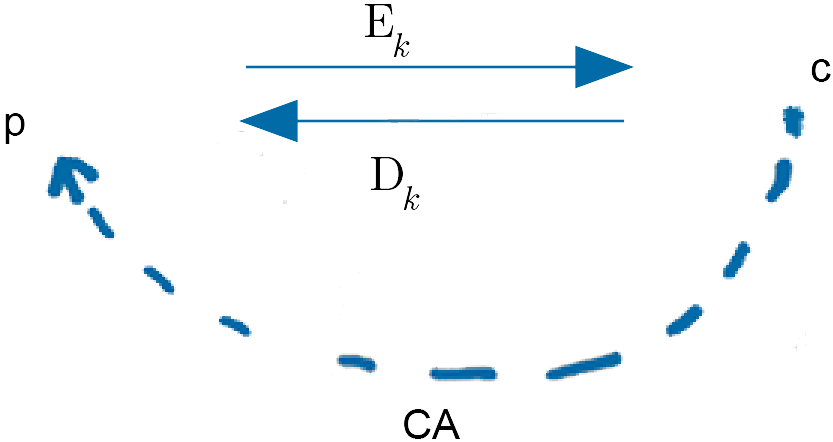
The key, $k$, is not known to the hacker. Both the plaintext, $p$, and the ciphertext, $c$, are character strings from some character set ( or alphabet ). So the character set has a finite set of characters. The key is used to parameterise the encryption process. The key is one of many possible keys. Both $E_k$ and $D_k$ define functions between sets of character strings. Also, $D_k$ is the inverse process of $E_k$, i.e. $D_k = E_k^{-1}$.
Two Main Groups of Ciphers
Ciphers can be categorised into two main groups:
stream cipher
Here each plaintext character is taken one by one and transformed by some method into ciphertext.block cipher
Here predetermined groups of characters are taken at a time and transformed into ciphertextCaesar Cipher
The Caeser cipher is an example of a shift cipher. Here, replace A by D, B by E, C by F, etc
number 0 1 2 3 4 5 6 7 8 9 10 plaintext A B C D E F G H I J K ciphertext D E F G H I J K L M N number 11 12 13 14 15 16 17 18 19 20 plaintext L M N O P Q R S T U ciphertext O P Q R S T U V W X number 21 22 23 24 25 plaintext V W X Y Z ciphertext Y Z A B C By setting numerical values to the alphabet so that $A = 0,\, B = 1,\, C = 2,\, \ldots ,\, Z = 25$, it can be seen that the Caesar cipher is just a shift.
$y = (x + 3) (mod\; 26)$
For $A = 0$ in plaintext, set $x = 0$ and so $y = (0 + 3) (mod\; 26) = 3$. hence, the ciphertext is $3 = D$.
Similarly, $Z = 25$ in plaintext, $y = (25 + 3)(mod \;26) = 2$, so the ciphertext is $C = 2$.
To convert the plaintext “HI THERE” to ciphertext, ignore the space after HI and we have:
Plaintext H I T H E R E
Numerical $7 \;\;\; 8 \;\;\; 19 \;\;\; 7 \;\;\; 4 \;\;\; 17 \;\;\; 4$
$(x + 3)(mod \;26)$
Numerical $10 \;\;\; 11 \;\;\; 22 \;\;\; 10 \;\;\; 7 \;\;\; 20 \;\;\; 7$
Ciphertext K L W K H U H
To decipher this message, we just use
$y = (x - 3) (mod \;26)$
A hacker could simply try out all of the possible shifts $1 \rightarrow 25$ until one of these shifts produced a message that made sense. Using a computer for this process would take seconds and the code is cracked.
Alternatively, a hacker could use facts about the letter frequency in English to find a highly likely substitution for one letter. So by finding one substitution letter, the code can be cracked.
By looking at shift type ciphers mathematically, we can easily use a computer (e.g. spreadsheet) to solve shift type ciphers.
So shift ciphers are not secure.
-
Modular Arithmetic
Imagine a clock with say four numbers $\{ 0, 1, 2, 3 \}$
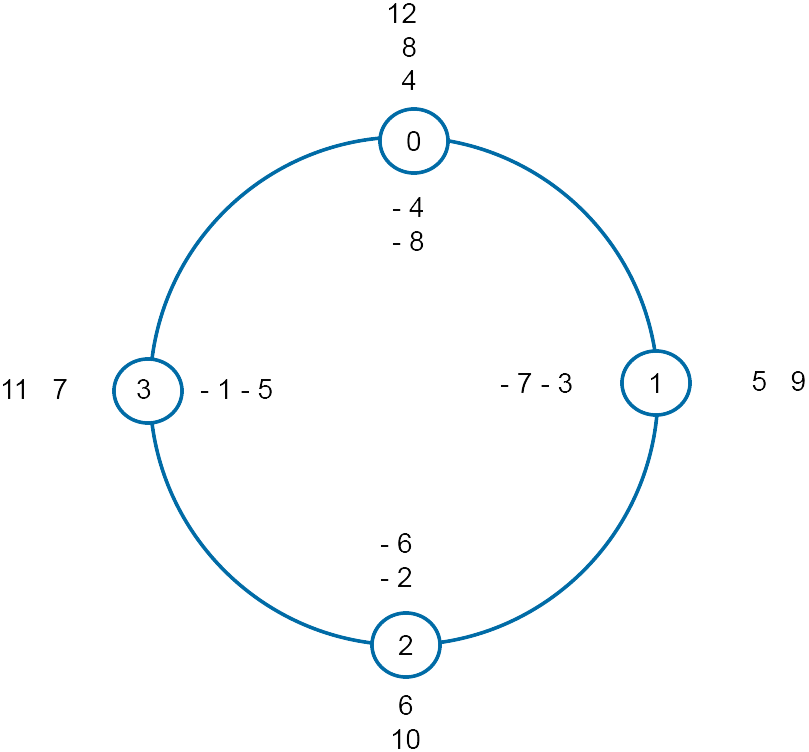
Go round the clock and write down the numbers $0, 1, 2, 3$. The number $4$ lands on $0$, the number $5$ lies on $1$, and so on.
With negative numbers, start at $0$, and go back one at a time.
We have just written out some of the numbers for $\mathbb{Z}_4$
Residue class [0] contains $\{ \ldots, -8, -4, 0, 4, 8, \ldots \}$
Residue class [1] contains $\{ \ldots, -7, -3, 1, 5, 9, \ldots \}$
Residue class [2] contains $\{ \ldots, -6, -2, 2, 2, 6, \ldots \}$
Residue class [3] contains $\{ \ldots, -5, -1, 3, 7, 11, \ldots \}$
Let’s select one of these residue classes, let’s pick [3].
Now in $\mathbb{Z}_4$
${\Large\frac{11}{4}} = 2\; \text{Rem}\; 3$, ${\Large\frac{7}{4}} = 1 \; \text{Rem}\; 3$, ${\Large\frac{3}{4}} = 0 \; \text{Rem} \; 3$
Notice that this division gives the same remainder. So all of the numbers in [3] are related. When divided by $4$ they give the same remainder.
We write
$7 \equiv 3 \; (mod \; 4)$
↑
is congruent to
let’s look at the negative numbers in [3]
Now ${\Large\frac{-1}{4}} = 0 \; \text{Rem} \; 1$, This is not helpful
re-write $-1 = -1 + 0 = -1 + (-3 + 3) = -4 + 3$
So now ${\Large\frac{-4 + 3}{4}} = -1 \; \text{Rem} \; 3$
Also $-5 = -5 + (-3 + 3) = -8 + 3$
${\Large\frac{-8+3}{4}} = -2 \; \text{Rem} \; 3$
So all of the negative numbers in [3] give a remainder of $3$ when divided by $4$.
Now we can write
$-5 \equiv 3 (mod \; 4)$
also $7 \equiv -1 (mod \; 4)$, etc.
For every number in [3], that number is congruent to $3$
Example
Is $59 \equiv 3 \; (mod \;4)$?
Now ${\Large\frac{59}{4}} = 15 \; \text{Rem} \; 3$, As the remainder is $3$ this is true.
End of ExampleExample
Is $71 \equiv 3 \; (mod \;4)$?
Now ${\Large\frac{71}{4}} = 17 \; \text{Rem} \; 3$, This is true.
End of ExampleCayley Addition Table and Multiplication Table for $\mathbb{Z}_4$
Addition Multiplication $+$ 0 1 2 3 $\times$ 0 1 2 3 0 0 1 2 3 0 0 0 0 0 1 1 2 3 0 1 0 1 2 3 2 2 3 0 1 2 0 2 0 2 3 3 0 1 2 3 0 3 2 1 Cayley Addition Table and Multiplication Table for $\mathbb{Z}_5$
Addition Multiplication $+$ 0 1 2 3 4 $\times$ 0 0 0 0 0 0 0 1 2 3 4 0 0 0 0 0 0 1 1 2 3 4 0 1 0 1 2 3 4 2 2 3 4 0 1 2 0 2 4 1 3 3 3 4 0 1 2 3 0 3 1 4 2 4 4 0 1 2 3 4 0 4 3 2 1 Inverse for Multiplication
in normal arithmetic, the multiplicative inverse of a number is its inverse.
$$x \;\; \frac{1}{x} \;\;x^{-1}, \;\;\;\; \text{Note} \; (x)\Big(1\Big/x\Big) = 1 $$ $$2 \;\; \frac{1}{2} \;\; 2^{-1}, \;\;\;\;\;\;\;\;\;\;\;\;\;\; (2)\Bigg(\frac{1}{2}\Bigg) = 1$$ $$10 \;\;\frac{1}{10}\;\; 10^{-1}, \;\;\;\;\;\;\;\;\; (10)\Bigg(\frac{1}{10}\Bigg) = 1$$
However, in module arithmetic, there are no fractions.
In $\mathbb{Z}_4, \;\; (1)(1) = 1$ and $(3)(3) = 1$
So $1^{-1} = 1, 3^{-1} = 3$
However, in $\mathbb{Z}_4,\;\; 2^{-1}$ does not exist.
In $\mathbb{Z}_5 , 1^{-1} = 1 , 2^{-1} = 3, 3^{-1} = 2, 4^{-1} = 4$
So what is the difference between $\mathbb{Z}_4$ and $\mathbb{Z}_5$ ?
The number $5$ is a prime number and this property ensures that all numbers in $\mathbb{Z}_5$ have an inverse (apart from $0$ of course).
-
Affine Cipher
As the letters in shift ciphers are not mixed up enough, they offer little security. The idea behind affine ciphers is to use multiplication combined with addition to create a more ‘mixed-up’ substitution.
In general, an affine cipher uses the following formula to encrypt plaintext:
$y = ( kx + b )\; ( mod\; m )$
Where $m$ is the number of letters in the character set ( for us for the moment $m = 26$ ) and $k$ and $b$ are chosen from among the integers $0, 1, 2, 3, \ldots, m -1$.
$x$ is the equivalent of a plaintext letter (numerical value) and $y$ is the numerical equivalent of the corresponding ciphertext letter.
Decimation Cipher
This is a special case of an affine cipher in which the constant $b = 0$.
$y = kx \;(mod\; m )$
In $\mathbb{Z}_{26},\; y = kx\; ( mod\; 26 )$
Using this to transform the letters of the alphabet gives for $k = 3$.
plaintext A B C D E F G H I J K L M N numberp 0 1 2 3 4 5 6 7 8 9 10 11 12 13 numberc 0 3 6 9 12 15 18 21 24 1 4 7 10 13 plaintext A D G J M P S V Y B E H K N plaintext O P Q R S T U V W X Y Z numberp 14 15 16 17 18 19 20 21 22 23 24 25 numberc 16 19 22 25 2 5 8 11 14 17 20 23 plaintext Q T W Z C F I L O R U X In this method for $k = 3$
$A \rightarrow A$ and
$N \rightarrow N$
There are two collisions ( a plaintext letter encrypts as itself ).
However, a hacker trying a systematic attack treating this as a shift type ciphertext would not obtain a sensible message.
By examining frequency counts, a good hacker can distinguish between transposition and substitution ciphers.
Try $k = 4$
With $k = 4$, we have for the letters A nd N:
plaintext A N
numberp 0 13
$y = 4x\; (mod \;26)$
numberc 0 0
ciphertext A A
As both A and N have ciphertext A, using $k = 4$ is useless
Also $B \rightarrow E$ and $O \rightarrow E$.
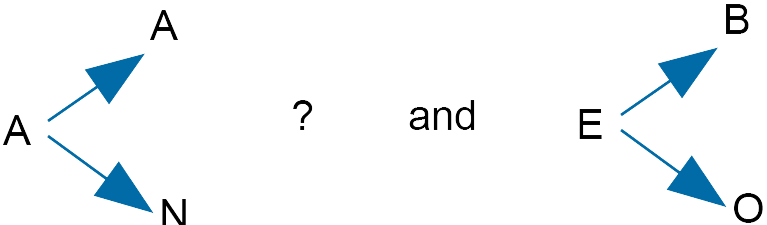
The reason for this problem is that $26 = (2)(13)$. If an integer contains a factor of $26$ then
$4x \equiv 0 \; (mod \; 26)$
Set $x = 0$ and then set $x = 13$.
Try $k = 6$
With $k = 6$, we have for the letters A and N:
plaintext A N
numberp 0 13
$y = 4x\; (mod \;26)$
numberc 0 0
ciphertext A A

Note that $6 = (2)(3)$ and $2$ is a factor of $26$ and so
$6x \equiv 0 \; (mod \;26)$
For $x = 0$, this is true; for $x = 13$ this is also true.
Sensible Values in k in $\mathbb{Z}_{26}$
Using a 26 letter alphabet, we can set $k = 1, 3, 5, 7, 9, 11, 15, 17, 19, 21, 23$ or $25$.
Ignoring $k = 1$, there are only 11 decimation ciphers. Using a spreadsheet, it is easy to crack these codes.
Decrypting Affine Cipher
An affine cipher is a composition of a decimation followed by a shift. If the number ‘a’ is relatively prime to 26 and the number ‘b’ lies in the range of 0 to 25, then an affine number cipher is given by:
$y \equiv (ax + b) \;(mod \; 26)$
$\Rightarrow(y-b) \equiv ax (mod \; 26)$
As ‘a’ is relatively prime to 26, then ‘ a-1’ exists
$\Rightarrow a^{-1}(y-b) \equiv ax \; (mod \; 26)$
hence
$x \equiv a^{-1} (y-b)(mod \;26)$
This is the formula to decrypt the affine cipher.
Now there is another problem in $\mathbb{Z}_{26}$ and this is checking if ‘a’ is relatively prime to $26$. For $\mathbb{Z}_{26}$ this is fairly easy to solve, but what if you wanted to use $\mathbb{Z}_{256}$ or $\mathbb{Z}_{4197}$?
The best solution is to use prime numbers, e.g. $\mathbb{Z}_{29}$, $\mathbb{Z}_{31}$, etc as the ‘$a^{-1}$’ exists.
Example
Suppose we wish to send the message “SEND MONEY” using the formula
$y = (7x + 4)\; (mod \; 26)$
The reply in ciphertext is “EDD AFGRH”
Encrypt the first mesage and decrypt the reply.
Solution
plaintext S E N D M O N E Y numericalp$ 18 4 13 3 12 14 13 4 25 numericalc 0 6 17 25 10 24 17 6 16 ciphertext A G R Z K Y R G Q Now in $\mathbb{Z}_{26} \; 7^{-1}$ is $15$.
check $(7)(15) = 105$, ${\Large\frac{105}{26}} = 4 \;\text{Rem}\; 1$
So $(7)(15) \equiv 1( mod\; 26 )$
ciphertext E D D A F G R H numericalc 4 3 3 0 5 6 17 7 $x \equiv 15 (y-4)(mod \; 26)$
numericalp 0 11 11 18 15 4 13 19 plaintext A L L S P E N T Password Encrypt
Using the principles of modular arithmetic, it is possible to encrypt plaintext using some password.
For each letter in the plaintext, each letter in the password is combined using modular arithmetic.
The encryption process is as follows:
$(x + S) (mod \;26),\;\; \mathbb{Z}_{26}$
Where $x$ represents a letter in the plaintext and S represents a letter in the password.
End of ExampleExample
Encrypt the text “PLEASE KEEP LEFT” with the password “SECURITY”.
Solution
plaintext P L E A S E K E E P L E F T numericalp 15 11 4 0 18 4 10 4 4 15 11 4 5 19 password S E C U R I T Y S E C U R I numericalp 18 4 2 20 17 8 19 24 18 4 2 20 17 8 $(x+S)(mod \; 26)$
numericalc 7 15 6 20 9 12 3 2 22 19 13 24 22 1 ciphertext H P G U J M D C W T N Y W B Note: $( 15 + 18 )( mod\; 26 ) \equiv 33 ( mod\; 26) \equiv 7( mod\; 26 )$
Password Decrypt
To decrypt the previous ciphertext, each letter of the ciphertext is taken together with a letter from the password. The numbers are subtracted using modular arithmetic.
The decryption process is as follows:
$( x - S ) (mod\; 26 ),\; \mathbb{Z}_{26}$
End of ExampleExample
Decrypt the text “H P G U J M D C W T N Y W B” with the password “SECURITY”
Solution
ciphertext H P G U J M D C W T N Y W B numericalc 7 15 6 20 9 12 3 2 22 19 13 24 22 1 password S E C U R I T Y S E C U R I numericalp 18 4 2 20 17 8 19 24 18 4 2 20 17 8 numericalp 15 11 4 0 18 4 10 4 4 15 11 4 5 19 ciphertext P L E A S E K E E P L E F T Note: $( 7 - 18 ) = -11 ( mod\; 26 ) \equiv 15 ( mod\; 26 )$
This then gives the message that was encrypted in the previous example.
End of ExampleTransposing Data Blocks
In an attempt to jumble up the ciphertext, the ciphertext can be written as a block and using a transpose key, the ciphertext is mixed up further.
Example
Using the ciphertext H P G U J M D C W T N Y W B with a ‘transpose key’ of 4, encode the ciphertext.
Solution
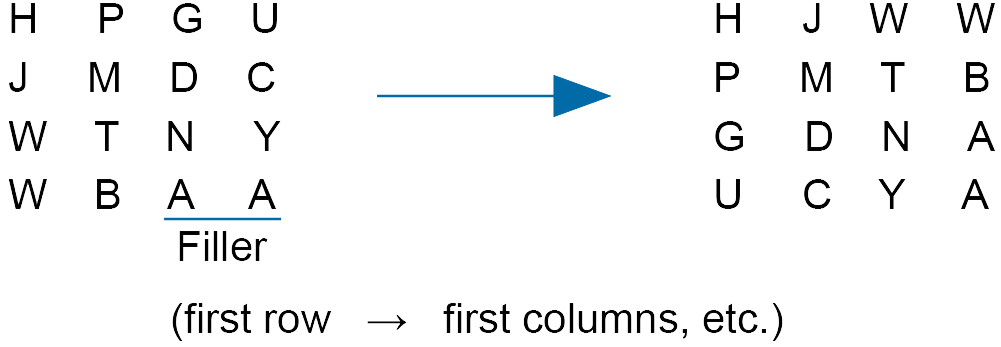
Now the ciphertext reads: H J W W P M T B G D N A U C Y A
This puts another obstacle in a hacker’s way.
Using a ‘transpose key’ of 5 gives
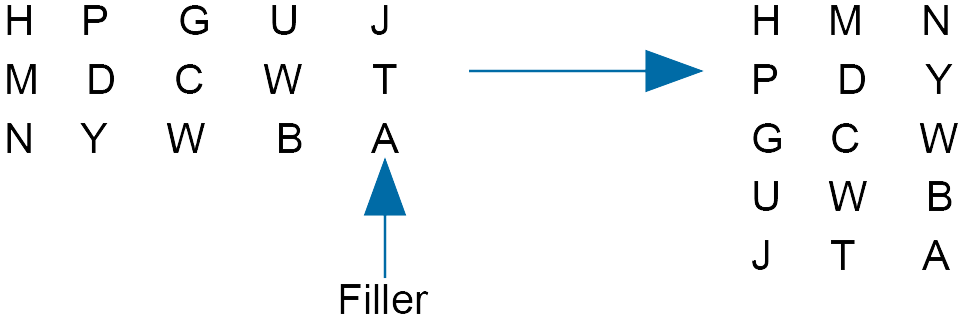
Now the ciphertext reads:
H M N P D Y G C W U W B J T A
Again, this mixes the ciphertext further.
End of Example -
$\mathbb{Z}_{26}$ and $\mathbb{Z}_{29}$
$\mathbb{Z}_{26}$
plaintext letter A B C D E F G H I J K L M N O P Q R S T U V W X Y Z plaintext number 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 $\mathbb{Z}_{29}$
plaintext letter A B C D E F G H I J K L M N O P Q R S T U V W X Y Z . ? ␣ plaintext number 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28