For the purposes of illustration, six numbers will be sorted. The numbers are mixed up in order and we will sort these into the order of smallest to largest.

Although numbers will be used, the sorting algoritm could be used on letters (lowercase and uppercase) other characters or on a mixture of numbers, letters and characters.

Consider the following six numbers:

$14\;\;\; 12\;\;\; 16\;\;\; 21\;\;\; 50\;\;\; 7$

Now what we will do is to split this list into two groups:

the first group will contain sorted numbers.

the second group will contain unsorted numbers

Then step by step, we will take a number from the unsorted group and put into its correct position in the sorted group.

We start by taking the first number in the list. This is put into the sorted group. As it is the only number in the sorted group, it must be sorted. The other numbers go into the unsorted group.

$14\;\;\; \mid \;\;\;12\;\;\; 16\;\;\; 21\;\;\; 50\;\;\; 7$

Now take the first number in the unsorted list. This is the number 12. Put this number into the sorted group. now we have.

$14\;\;\; 12\;\;\; \mid \;\;\; 16\;\;\; 21\;\;\; 50\;\;\; 7$

Compare 14 and 12. Clearly, 14 > 12 so swap 14 and 12. Now we have

$12\;\;\; 14\;\;\; \mid \;\;\; 16\;\;\; 21\;\;\; 50\;\;\; 7$

Now he sorted group contains the numbers 12 and 14 and they are in the correct order.

Next, the number 16 is moved into the sorted group.

$12\;\;\; 14\;\;\; 16\;\;\; \mid \;\;\;21 \;\;\; 50 \;\;\; 7$

Now compare 14 and 16. As 14 < 16 then the number 16 remains where it is.

The sorted group contains the numbers 12, 14 and 16. Moreover, they are all in the correct order.

Now the next number is moved into the sorted list.

$12\;\;\; 14\;\;\; 16\;\;\; 21\;\;\; \mid \;\;\;50\;\;\; 7$

As 16 < 21 , then the number 21 is left in the position.

Now the numbers are

$12\;\;\; 14\;\;\; 16\;\;\; 21\;\;\; \mid \;\;\; 50 \;\;\; 7$

Now move the next number into the sorted list. This is the number 50.

$12\;\;\; 14\;\;\; 16\;\;\; 21\;\;\; 50\;\;\; \mid \;\;\; 7$

As 21 < 50, the number 50 remains in its position. Now the sorted numbers and unsorted numbers are

$12\;\;\; 14\;\;\; 16\;\;\; 21\;\;\; 50\;\;\; \mid \;\;\; 7$

Now the number 7 is moved into the sorted group.

$12\;\;\; 14\;\;\; 16\;\;\; 21\;\;\; 50\;\;\; 7\;\; \mid$

Now compare 50 and 7. As 50 > 7, the the order of these are swapped.

$ 12\;\;\; 14\;\;\; 16\;\;\; 21 \;\;\; 7 \;\;\; 50$

Now compare 21 and 7. As 21 > 7 swap the order

$12\;\;\; 14\;\;\; 16\;\;\; 7\;\;\; 21\;\;\; 50$

Now compare 16 and 7. As 16 > 7 swap the order.

$12\;\;\; 14\;\;\; 16\;\;\; 7\;\;\; 21\;\;\; 50$

Now compare 14 and 7. As 14 > 7 swap the order

$12\;\;\; 7 \;\;\; 14\;\;\; 16\;\;\; 21\;\;\; 50$

Now compare 12 and 7. As 12 > 7 swap the order

$7 \;\;\; 12 \;\;\; 14 \;\;\; 16 \;\;\; 21 \;\;\; 50$

As the number 7 is now in the first position, then there are no more numbers to compare it to. Hence, we stop and the list is now sorted from lowest number to highest number:

$7 \;\;\; 12 \;\;\; 14 \;\;\; 16 \;\;\; 21 \;\;\; 50$

Some Observations

If we now stop and have a think what has happened, we can see that:

there is a starting point.

there is a finishing point. So there are a finite number of steps.

the list is sorted. An unsorted list is input and a sorted list is output.

as each number moves from the unsorted group into the sorted group, it is swapped over one by one until it finds its correct position in the sorted list.

overall, there are step by step instructions which are precise and take us from an unsorted list to a sorted list.

if the unsorted list were shorter or longer, the algorithm would still work. So the method does not just work for our unsorted list. It works for any unsorted list, regardless of size.

Questions

We can start to ask some questions.

1) How good is the algorithm?

It works. Is it faster or slower than other methods? At this stage we do not know because this is a first sorting algorithm that we have looked at.

2) What would happen if the list was very large?

Suppose we wanted a sorted list of all the telephone numbers in the UK.

Suppose we want a register of births, deaths and marriages.

Suppose a company wanted to have an analysis of the size of customer orders over the last five years.

3) In our example of six numbers, how many comparisons were there and how many swaps?

4) If the initial order had been

$50\;\;\; 21\;\;\; 16\;\;\; 14\;\;\; 12\;\;\; 7$

how many comparisons and swaps are required?

So there are $1 + 2 + 3 + 4 + 5$ comparisons and swaps.

5) Is it possible to speed up the algorithm from a programming viewpoint?

Suppose the small number that has just entered the sorted list is copied to a temporary location. As comparisons are made, the larger numbers are moved to the right. Only when a number is smaller do we write a number to its location. In this way the number of “writes” can be reduced.

6) Are there any mathematical tools that allow a fast result of

$1 + 2 + 3 + 4 + 5$ ?

For a small list, it probably does not matter. However, what happens for some large $n$?

7) The original six numbers were partially sorted. The

$12\;\;\; 16\;\;\; 21\;\;\; 50$

are in a sorted order. What affect does this have on the algorithm?

8) What would happen if a number appeared more than once? Suppose we have two 5s or three 5s spread through the list. Do the 5s get swapped with one another?

This leads us into stability issues.

For the purposes of illustration, let’s keep the same six numbers in the unsorted list. Consider the six numbers:

$14\;\;\; 12\;\;\; 16\;\;\; 21\;\;\; 50\;\;\; 7$

Now what we will do is take the first two numbers and if the second number is smaller than the first number, they will be swapped.

Then we wil take the second and third numbers. If the third number is smaller than the second number then they are swapped.

This process will take the largest number to the top in the first pass.

In the second pass of the algorithm, the next largest number “bubbles” to the next largest location.

So the numbers are:

$\mid \;\;14 \;\;\; 12 \;\; \mid \;\; 16 \;\;\; 21 \;\;\; 50 \;\;\; 7$

Compare 14 and 12. If 14 > 12 then swap.

So the numbers are:

$12 \;\; \mid \;\;14 \;\;\; 16 \;\; \mid \;\; 21 \;\;\; 50 \;\;\; 7$

Compare 14 and 16. As they are in order, leave them.

Now the numbers are

$12 \;\;\; 14 \;\; \mid \;\;16 \;\;\; 21 \;\; \mid \;\;\; 50 \;\;\; 7$

Compare 16 and 21. Again, leave them.

Now the numbers are

$12 \;\;\; 14 \;\;\; 16 \;\; \mid \;\; 21 \;\;\; 50 \;\; \mid \;\;\; 7$

Compare 21 and 50. Again leave them

Now the numbers are:

$12 \;\;\; 14 \;\;\; 16 \;\;\; 21 \;\; \mid \;\; 50 \;\;\; 7 \;\; \mid$

Compare 50 and 7. As 50 > 7, swap them.

Now the numbers are:

$12 \;\;\; 14 \;\;\; 16 \;\;\; 21 \;\;\; 7 \;\;\; 50 $

The number 50 is now at the top of the list and we just need to to sort the remaining five numbers.

Second Pass

Now the numbers are:

$\mid \;\;12 \;\;\; 14 \;\; \mid \;\;\; 16 \;\;\; 21 \;\;\; 7 \;\;\; 50 $

Compare 12 and 14. Leave them as they are because 12 < 14.

Now have

$12 \;\;\; \mid \;\; 14 \;\;\; 16 \;\; \mid \;\;\; 21 \;\;\; 7 \;\;\; 50 $

Again, as 14 < 16, leave the numbers in position.

Now have

$12 \;\;\; 14 \;\;\; \mid \;\;16 \;\;\; 21 \;\; \mid \;\;\; 7 \;\;\; 50 $

the 16 and 21 are compared. As 16 < 21 then they are left as they are.

Now

$12 \;\;\; 14 \;\;\; 16 \;\;\; \mid \;\; 21 \;\;\; 7 \;\; \mid \;\;\; 50 $

As 21 > 7, these two numbers are swapped.

We now have

$12 \;\;\; 14 \;\;\; 16 \;\;\; 7 \;\;\; \underline{21 \;\;\; 50}$

Now 21 and 50 are at the top in the correct order.

Third Pass

The numbers are now:

$\mid \;\; 12 \;\;\; 14 \;\; \mid \;\;\; 16 \;\;\; 7 \;\;\; 21 \;\;\; 50$

Compare 12 and 14. As 12 < 14, leave them in position.

Now compare

$12 \;\;\; \mid \;\; 14 \;\;\; 16 \;\; \mid \;\;\; 7 \;\;\; 21 \;\;\; 50$

14 and 16. Again as 14 < 16, leave them in position.

Now compare

$12 \;\;\; 14 \;\;\; \mid \;\; 16 \;\;\; 7 \;\; \mid \;\;\; 21 \;\;\; 50$

As 16 > 7, we swap them. The list now looks like:

$12 \;\;\; 14 \;\;\; 7 \;\;\; \underline{16 \;\;\; 21 \;\;\; 50}$

Now 16, 21 and 50 are at the top in the correct order.

Fourth Pass

Now the numbers have the order

$\mid \;\; 12 \;\;\; 14 \;\; \mid \;\;\; 7 \;\;\; 16 \;\;\; 21 \;\;\; 50$

Compare 12 and 14. As 12 < 14, then leave them in position.

Now compare

$12 \;\;\; \mid \;\; 14 \;\;\; 7 \;\; \mid \;\;\; 16 \;\;\; 21 \;\;\; 50$

As 14 > 7, swap them.

$12 \;\;\; 7 \;\;\; \underline{14 \;\;\; 16 \;\;\; 21 \;\;\; 50}$

Now 14, 16, 21 and 50 are at the top in the correct order.

Fifth Pass

Now the numbers have the order

$\mid \;\; 12 \;\;\; 7 \;\; \mid \;\;\; 14 \;\;\; 16 \;\;\; 21 \;\;\; 50$

Compare 12 and 7. As 12 > 7, swap them.

Now the order is

$7 \;\;\; 12 \;\;\; 14 \;\;\; 16 \;\;\; 21 \;\;\; 50$

The numbers are now in order, bottom to top.

Some Observations

Like the insertion sort, the bubble sort has a start point and a finish point. There are step by step instructions and when these are followed an unsorted list is sorted.

The insertion sort and the bubble sort use different mechanisms to sort the numbers, but the output is the same.

Questions

1) How many comparisons and how many swaps were done?

Note that this

$5 + 4 + 3 + 2 + 1$

has re-appeared, but it is in the bubble sort

2) if the intial order had been

$50 \;\;\; 21 \;\;\; 16 \;\;\; 14 \;\;\; 12 \;\;\; 7$

How many comparisons and swaps are required?

So the worst possible case is when the list is already sorted from top to bottom and we want it sorted bottom to top.

3) The number of comparisons and swaps for the insertion sort and the bubble sort in the worst possible case is

$5 + 4 + 3 + 2 + 1$ for both comparisons and swaps.

In the work with the bubble sort and the insertion sort, the series

$1 + 2 + 3 + 4 + 5$

appeared.

Whilst it is trivial to add these numbers up, what if we had:

$1 + 2 + 3 + \ldots + n$

Where $n$ is some large number. for example, what if $n = 1000, n = 10,000, n = 1,000,000$?

Let’s consider $1 + 2 + 3 + 4 + 5$. Let’s suppose that the sum of these numbers is $S_5$.

Then

$S_5 = 1 + 2 + 3 + 4 + 5$

also $\underline{S_5} = \underline{5 + 4 + 3 + 2 + 1}$

add $\underline{2S_5} = \underline{6 + 6 + 6 + 6 + 6}$

$\Rightarrow 2S_5 = (5)(6) = 30$

$\Rightarrow S_5 = {\Large\frac{30}{2}} = 15$

So by reversing the order of the numbers and adding them to the original listed numbers, we can quickly add them.

Example 1

Example 2

Example 3

Example 4

Example 5

Arithmetic Progressions and Series

These wee tricks as shown in Example 5 are all well and good, but is there some way to avoid having to produce tricks?

Let’s re-look at the structure of the problem.

We have

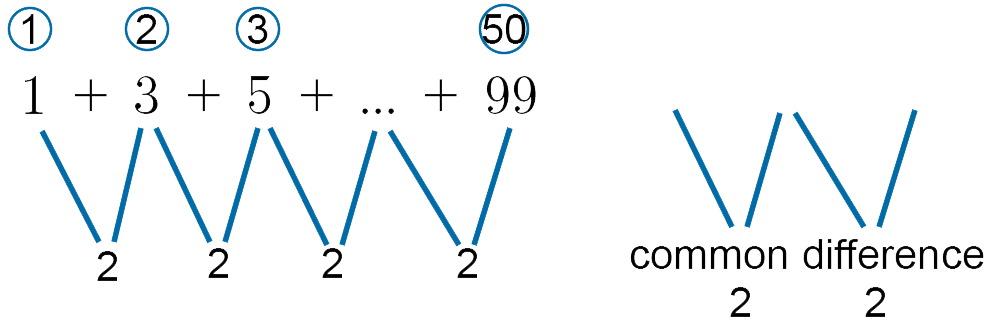
We can see that $(3 - 1) = 2$

also $(5 - 3) = 2$

So between successive numbers, the common difference is 2. The first number is 1 and the 50th Number is 99.

Let the first number be $a$

The second number number will be $a + d$, where $d$ is the common difference.

The third number will be $(a + d) + d = a + 2d$

The fourth number will be $(a + 2d) + d = a + 3d$

The 50th number will be $(a + (50 - 2)d) + d$

$= a + 49d$

$= a + (50 - 1)d$

Suppose we now want to add up the first n odd number. Then

$S_{n,odd} = a$ $+(a+d)+(a+2d)+\ldots+(a + (n-1)d)$

$\underline{S_{n,odd}} = \underline{(a + (n-1)d)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\, + \ldots + \;\;\;\;\;\;\;\;\;a }$

$S_{n,odd} = (2a + (n-1)d) + \ldots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;+ (2a + (n-1)d);n \;\text{of} $

$\therefore S_{n,odd} = {\Large\frac{(n)(2a + (n-1)d)}{2}}$

let’s use this formula to add up

$1 + 3 + 5 + \ldots + 99$

here the first number $a = 1$

The common difference $d = 2$

The number of numbers $n = 50$

$\therefore S_{n,odd} = {\Large\frac{(50)((2)(1) + (50-1)(2))}{2}}$

$= {\Large\frac{(50)(2 + (49)(2))}{2}}$

$= (50)(50)$

$= 2500$

This is the same result as before. However, we now have a ‘stronger’ way of adding up.

Sum to $n$ terms

When we look back at the formula, the first number $a$ does not need to be odd. It can be any number. The common difference $d$ is positive if the numbers are increasing and is negative if the numbers are decreasing. The number of numbers $n$ sometimes needs to be determined and care should be taken in doing this.

Example 6

Example 7

Example 8

Back to Insertion Sort and Bubble Sort

When sorting 6 numbers, the series

$ 1 + 2 + 3 + 4 + 5$

emerged from an analysis of sorting 6 numbers.

Now $5 = 6 - 1$ and $S_5 = {\Large\frac{(5)(6)}{2}} = {\Large\frac{30}{2}} = 15$

What if we sorted n numbers, The series

$1 + 2 + 3 + \dots + (n - 1)$

would appear from an analysis of the algorithms

Now $S_{n-1} = {\Large\frac{(n-1)(n)}{2}} = {\Large\frac{n^2 - n}{2}} = {\Large\frac{n^2}{2}} - {\Large\frac{n}{2}}$

The term ${\Large\frac{n^2}{2}}$ grows much faster in size than ${\Large\frac{n}{2}}$ as $n$ becomes larger. So from the point of view of asymptotic behaviour of a function, the ${\Large\frac{n}{2}}$ can be ignored because the ${\Large\frac{n^2}{2}}$ dominates ${\Large\frac{n}{2}}$.

Let’s suppose it takes one time tick to do one swap and one time tick to do a comparison.

Then, as $n$ increases

As strange as it may seem, adding up squares of numbers can come about in a very natural way.

In the days of forts firing cannonballs from cannons, the cannonballs can be stacked in layers.

For example, if the bottom layer is $4 \times 4$ cannonballs, then the top will be $3 \times 3$ cannonballs, and on top of that are $2 \times 2$ cannonballs and on top of that is a single cannonball.

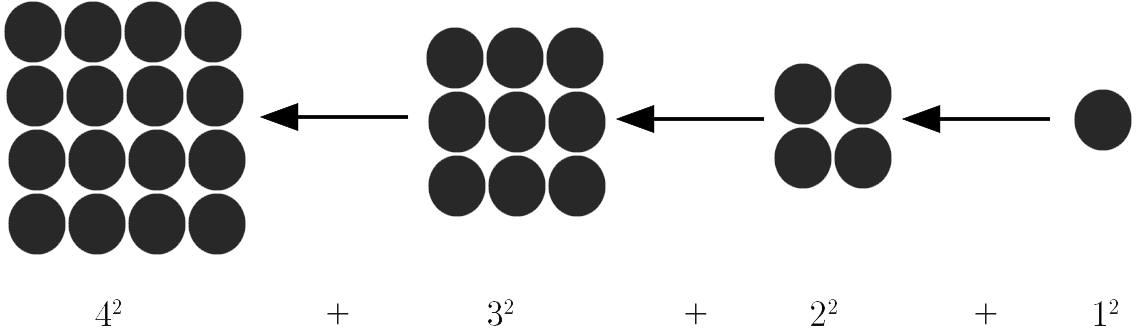
Now deriving the sum of these squares is beyond the scope of this module. However, the result of such an addition is used later in the notes.

$1^2 + 2^2 + 3^2 + \ldots + n^2 = {\Large\frac{n(n+1)(2n+1)}{6}}$

Example 9

Example 10

Adding Mathematical Series

Shorthand notation is used to add series of numbers. For example,

$$1 + 2 + 3 + 4 + 5 = \sum_{1=1}^{5}i$$

means start at $i = 1$, then $i = 2$, then $i = 3$ then $i = 4$ and finally $i = 5$

$$\text{So}\; \sum_{i=1}^{5}i = 1 + 2 + 3 + 4 +5$$

Example 11

Example 12

Example 13

Example 14

Example 15

Double summations can be formed

Example 16

In general, algorithms have certain properties.

The precision of the individual step by step instructions.

The input provided to the algorithm and the output the algorithm provides.

The ability of the algorithm to solve a certain type of problem - not just specific examples of the problem.

The uniqueness of the intermediate and final results - based on the input.

The finite nature of the algorithm in that it terminates after the execution of a finite number of steps.

When an algorithm correctly solves a certain type of problem and satisfies the above conditions, then the algorithm can be examined further.

Measure how long (no. of steps) it takes to solve a problem of a certain size.

If several algorithms are available, which is best? How do we determine this?

Example 1

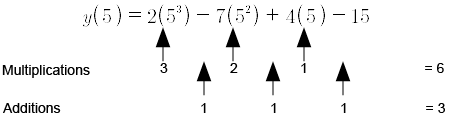
Let $y(x) = 2x^3 = 7x^2 + 4x - 15$

Determine $y(5)$

Solution

Method 1

Method 2

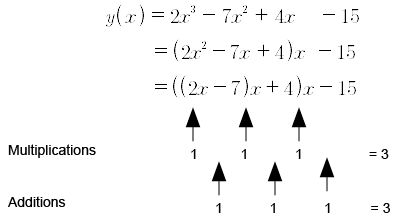
A comparison of the two methods shows:

Multiplications Additions

Method 1 63

Method 2 33

In general, it can be shown that for a polynomial of degree $n$:

Multiplications Additions

Method 1 ${\Large\frac{n(n+1)}{2}}$$n$

Method 2 $n$$n$

Doing just a few calculations, it would not matter which method is used

If the polynomial is of degree 100 and 10,000 such calculations are required, then

Multiplications Additions

Method 1 50,500,0001,000,000

Method 2 1,000,0001,000,000

The analysis of algorithms is a major task in computer science.

The ‘efficiency’ or ‘complexity’ of an algorithm is measured by counting the number of key operations.

End of Example 1

Examples

In sorting and searching - count comparisons

In arithmetic - count multiplications

ignore additions

The complexity of an algorithm is often denoted by a function, $f(n)$, which gives the running time | no, of steps | storage space requirements of the algorithm in terms of the size n of the input data. (Usually running time for a given computer system).

The complexity function, $f(n)$ of an algorithm increases as $n$ increases.

Usually the main interest is in the rate of increase of $f(n)$.

This rate of increase is usually done by comparing $f(n)$ with some standard function.

e.g. $log_2n,\;\;\; n,\;\;\; nlog_2n,\;\;\; n^2,\;\;\; n^3,\;\;\; 2^n$

The ‘Big Oh’ notation is used to compare complexity functions.

Example 2

Example 3

Example 4

Example 5

Example 6

Example 7

Often we want to find if a list contain a particular item.

Such a search will return either a true or false

if in the list, the position of the item is found.

    input n, array, target
    for i = 1 to n
        test: target = array(i)
    return i
    else return - 1, (not found)

In the best case, the target will be the first element of the array. So here, only one comparison is made.

In the worst case the target is at the last position or the target is not in the array. So here, n comparisons are made.

What’s the average case?

Is it

$$\frac{\text{(best case + worst case)}}{2}$$ $$= \frac{(1 + n)}{2} = \frac{(n + 1)}{2}$$

If target is equally likely to occur in the array in any position, then the probability that it occurs in position $1$ is $1/n$, in position $2$ is $1/n$, etc

Hence using these probabilities

$f(n) = (1)\Big({\Large\frac{1}{n}}\Big)+(2)\Big({\Large\frac{1}{n}}\Big)+, \ldots + n\Big({\Large\frac{1}{n}}\Big)$

$$ = (1 + 2 + \ldots + n)\Big(\frac{1}{n}\Big) $$ $$= \frac{n(n+1)}{2}\Big(\frac{1}{n}\Big) $$ $$= \Big(\frac{n+1}{2}\Big),\;\; \text{as before} $$

In the calculation of $f(n)$, we have made some assumptions. In certain cases, these assumptions may not hold.

Another linear search with different assumptions

Suppose that though some experience of searching through outrlist, we know that

The target is not in the array half the time. So half the time we search through the entire array.

If it is the array then there is an equal probability of the target being at any array position.
Pr ( Target being in location $i$ ) $= 1/n$

So if the target is not in the array, we search through $n$ times with a probability of 0.5.

If the target is not in the array, the expected number of comparisons, $E$, is given by

$E = 1 \times {\Large\frac{1}{n}} + 2 \times {\Large\frac{1}{n}} + 3 \times {\Large\frac{1}{n}} + \ldots + n {\Large\frac{1}{n}}$

$$= (1 + 2 + 3 + \ldots + n)\frac{1}{n}$$ $$= \frac{n(n+1)}{2} \Big(\frac{1}{n}\Big) $$ $$= \frac{n+1}{2} $$

Putting these two results together

$$(0.5)n + (0.5)\Big(\frac{n+1}{2}\Big) = \Big(\frac{3n+1}{4}\Big) = f(n) $$

$f(n)$ represents the average number of comparisons.

Search of the sorted list - Binary Search

Suppose the list is sorted.

Psuedo code for the search is :-

input array, n ,target
integer low, high mid
low !=0, high !=n-1, mid !=0
while (low < high)
         (mid != (low +high)/2
          if test target = array(mid)
              then return mid.
          elseif(target > array(mid))
               then low = mid + 1
          else (target < array(mid))
               then high = mid - 1
/while
return - 1;  target not found

There are three parts to this algorithm

initialisation

while loop

return

The number of times that the loop iterates depends on the size of input.

The best case is when the target is found on the first pass, target = array(mid).

The worst case is when the target is found at the very end of the algorithm. Informally, the mathematical question is

How many times can $n$ be divided by $2$ until you have $1$?”

So for some power of $2$, call it $x$, say we want

$$1 = \frac{n}{(2^x)} \Rightarrow 2^x = n $$

$\Rightarrow log_22^x \;\,= log_2n$
$\Rightarrow x\; log_22 = log_2n$
$\Rightarrow$$= log_2n$

If the list contains $8$ elements, then at worst we go around the while loop $log_28 = log_22^3 = 3\; log_22 = 3$ times

In general, in the worst case, $f(n) = log_2n$.

Comparison of Linear Search in Unsorted List Vs Search of Sorted List using Binary Search

For the linear search in the average case

$f(n) = {\Large\frac{n+1}{2}}$, ignoring the ${\Large\frac{1}{2}}$

$f(n) = {\Large\frac{n}{2}}$

For the binary search of a sorted list, the worst case is given by

$g(n) = log_2n$

$$\text{Note:}\;\; log_210 = \frac{log_{10}10}{log_{10}2} \approx \frac{1}{0.3010} \approx 3.32$$

$\text{and}\;\; log_2100 = log_210^2 = 2 \; log_210$

In computer programming, recursion is concerened with the ability of a function (or subroutine) to call itself.

Factorial Function

On of the best known recursive functions is the factorial function. This is defined as:

$n! = (n)(n-1)(n-2)\ldots(2)(1)$

$= (n)(n-1)!$

also $(n-1)! = (n - 1)(n - 2)!$ and so on

Example

Fibonacci Numbers

The Fibonacci number are also recursive.

The numbers start as follows:

$1, 1, 2, 3, 5, 8, 13, \ldots$

Now the first number $f_1 = 1$, the second number $f_2 = 1$.

The third number is formed as follows:

$f_3 = f_2 + f_1 = 1 + 1 = 2$

The fourth number is:

$f_4 = f_3 + f_2 = 2 + 1 = 3$

In general,

$f_n = f_{n-1} + f_{n-2}$

Strangely though, these numbers appear in computing and in biology in a natrual way.

Poisson Distribution

In the poisson distribution, the probability that a random variable $X$ takes a value of $k$ is:

$$Pr(X = k) = \frac{\lambda^k}{k!}e^{-\lambda} $$

$$= \frac{\lambda}{k} \frac{\lambda^{k-1}}{(k-1)!}e^{-\lambda}$$ $$= \frac{\lambda}{k}Pr(X = k - 1) $$

Clearly, this is another recursive function. As probability distributions are beyond the scope of this module, you do not have to study them. All that is important from the point of view of this module is that this is another recursive function.

Programming a Factorial Function

We might have an intial attempt at writing code as follows:

       declare function factorial (int n)
          return n × factorial (n -1)

If this psuedo code is tested, then we would have for example for $n = 3$:

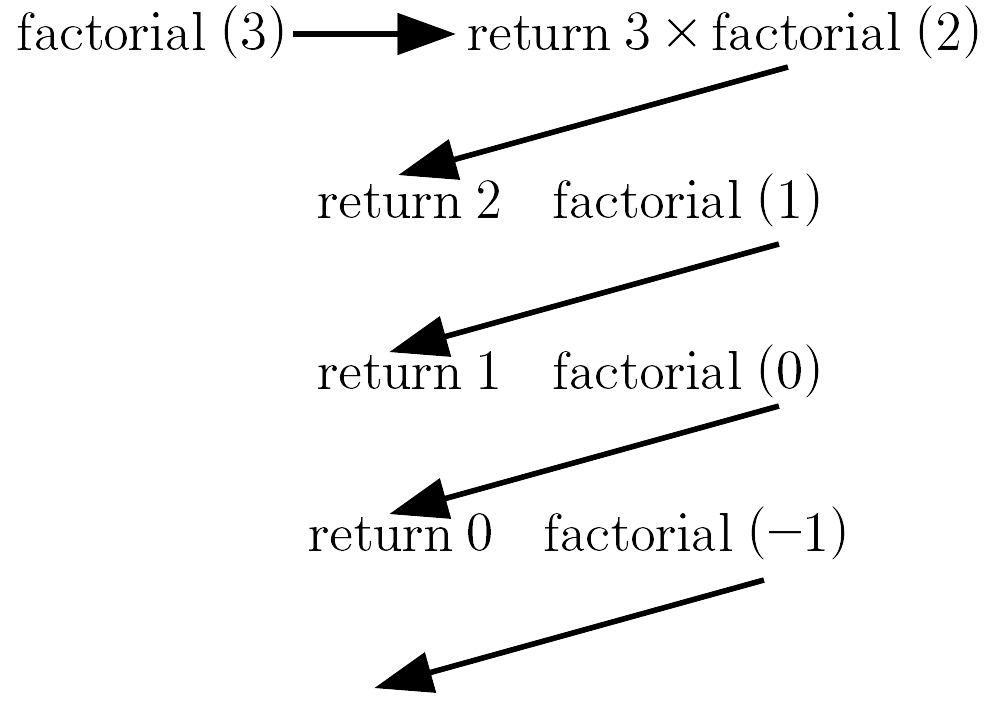
Clearly, there is a problem, as there is no end to the call of the function, the computer would eventually run out of stack space and crash

We need a halting case ( or base case ) and we need to deal with incorrect input.

The $n$ in the factorial function should not be less than $0$. If it is, an error value can be returned. Also $0! = 1$ and $1! = 1$.

So psuedo code could look like:

declare function factorial (int n)
   if n < 0 the return 0    // error code
      else if n = 0 or n = 1  return 1
      else return n × factorial (n - 1)

Now if we look at some examples

$\text{factorial} (-4) = 0 $; return 0, so it is an error

$\text{factorial} (0)\;\;\; = 1$

$\text{factorial} (1)\;\;\; = 1$

$\text{factorial} (4)\;\;\; = (4)(3)(2)(1) = 24$