-
1. Introduction
- This unit introduces the theory and application of mathematical structures known as matrices. With the advent of computers matrices have become widely used in the mathematical modelling of practical real-world problems in computing, engineering and business where, for example, there is a need to analyse large data sets. Applications of matrices occur:
- in all areas of science to solve (large) systems of equations.
- in computer graphics to project three dimensional images onto two dimensional screens and apply transformations to rotate and move these screen objects.
- in cryptography to encode messages, computer files, PIN numbers, etc.
- in business to formulate and solve linear programming problems to optimise resources subject to a set of constraints.
-
2. Definitions
Before we undertake calculations involving matrices it is firstly necessary to present some definitions and terminology.
2.1. What is a matrix?
A matrix is an ordered rectangular array of numbers and/or variables arranged in rows and columns and enclosed in brackets. For our purposes these elements will take the form of real numbers. In general, matrices are denoted by upper case letters.
Example 1
The following are all matrices:
(i). $A = \pmatrix {0 & \;\,\,4 \\ 1 & -1}$
(ii). $B = \pmatrix {\;50 & 25 & \;45 \\ 125 & 80 & \;60 \\ \;60 & 0 & \;75 \\ \;90 & 80 & 110}$.
(iii). $K = \pmatrix{\;\;\,1.2 & 3.8 & 0.2 & -0.2 & 3.1 \\ -2.3 & 2.1 & 3.6 & \;\;\,3.8 & 0.1}$
(iv). $M = \pmatrix{3 \\ 1}$.
End of Example 12.2. Rows and columns of a matrix
A useful interpretation of the structure of a matrix is to consider the rows and columns of the matrix. These are simple and obvious concepts; but we need to know that the rows are numbered starting from the top (i.e. Row 1) and the columns are numbered starting from the left hand side of the matrix (i.e. Column 1). For example, we have
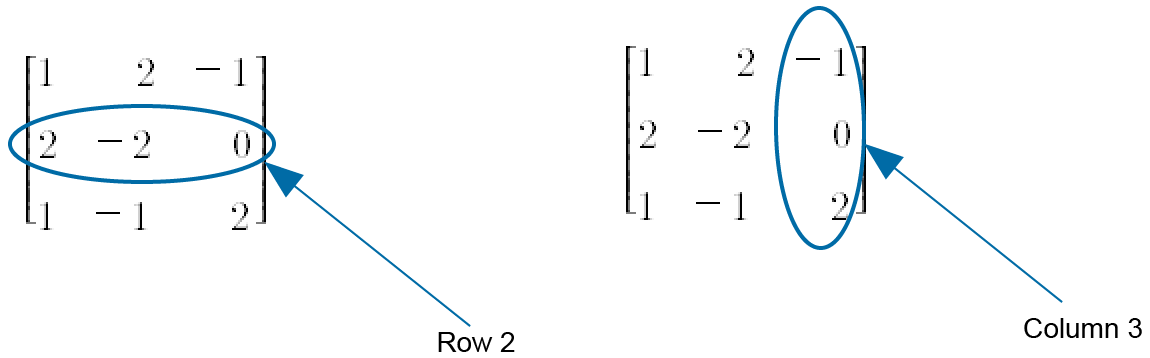
2.3. Order of a matrix
The size, also called the order or dimension, of a matrix is identified by a number pair in the form $m \times n$, where $m$ is the number of rows in the matrix and $n$ the number of columns.
$A = \pmatrix{a_{11} & a_{12} & \cdots & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & \cdots & a_{2n} \\ \vdots & & \ddots & & \vdots \\ \vdots & & & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & \cdots & a_{mn}} $
We say that the matrix $A$ is a “$m$ by $n$ matrix”.
A matrix with the same number of rows as columns, i.e. $m = n$, is called a square matrix.
Example 2
The matrices in Example 1 have the following sizes,
(i). $A$ is a $2 \times 2$ matrix, i.e. 2 rows and 2 columns.
(ii). $B$ is a $4 \times 3$ matrix, i.e. 4 rows and 3 columns.
(iii). $K$ is a $2 \times 5$ matrix, i.e. 2 rows and 5 columns.
(iv). $M$ is a $2 \times 1$ matrix, i.e. 2 rows and 1 column.
End of Example 22.4. Element of a matrix
Each element, or entry, in a matrix is denoted by a lower case letter with appropriate subscripts indicating its row and column position. Hence, element $a_{ij}$ is located in the $i$-th row and $j$-th column of the matrix $A$ as shown below.
$A = \pmatrix{a_{11} & a_{12} & \cdots & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & \cdots & a_{2n} \\ \vdots & & \ddots & & \vdots \\ \vdots & & & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & \cdots & a_{mn}} $
Example 3
For the matrix $A = \pmatrix{\;\,50 & \;\;\,25 & -45 \\ \,125 & \;\;\,80 & \;\;\,60 \\ \;\;60 & -50 & \;\;\,75 \\ \;\,90 & \,120 & \,110 }$
(i). element $a_{43} = 110$, as it is located at Row 4, Column 3.
(ii). element $a_{32} = -50$ , as it is located at Row 3, Column 2.
We can easily draw parallels between matrices and computer arrays as used in programming languages. For example, in C++ if $A$ is an array we would use the syntax $A[2][3]$ to index the element in the second row and third column of $A$, in Maple we would use the notation $A[2, 3]$ and in MATLAB we would write $A(2, 3)$.
End of Example 32.5. Equality of matrices
- Two matrices $A$ and $B$ are equal if and only if:
- they are of the same size, i.e. both are $m \times n$ matrices
- their corresponding elements are the same, i.e. $a_{ij} = b_{ij}$ for $i = 1, ..., m$ and $j = 1,...,n$.
Example 4
Determine the values of $w, x, y$ and $z$ that guarantee the matrices $A$ and $B$ are equal,
$A = \pmatrix{4 & x \\ x+z & 0}$, $B = \pmatrix{y & 6 \\ 7 & w}$
Solution
We require $w = 0,\; x = 6,\; y = 4,\; x + z = 7 \implies z = 1$.
End of Example 4Now watch the following:
-
3. Operations with matrices
We now look at some basic arithmetic operations with matrices.
3.1. Matrix addition
- Two matrices can be added if and only if they are of the same size.
- To add two matrices we add corresponding elements.
- The result of the addition is a matrix of the same size.
- Matrix addition is commutative, i.e. $A + B = B + A$, see parts (ii) and (iii) in the following example.
Example 5
In each of the following carry out the specified addition.
(i). $\pmatrix{\;\;50 & \;\;25 & \;\;45 \\ 125 & \;\;80 & \;\;60 \\ \;\;60 & \;\;80 & \;\;75 \\ \;\;90 & 120 & 110} + \pmatrix {-50 & 35 & \;\;\,45 \\ -25 & 80 & -70 \\ -80 & 10 & \;\,-5 \\ \;\;\,90 & 20 & -135} = \pmatrix{\;\;\;0 & \;\;\,60 & \;\;\,90 \\ \,100 & \,160 & -10 \\ -20 & \;\;\,90 & \;\;\,70 \\ \,180 & \,140 & -25}$
(ii). $\pmatrix {2 & -1 \\3 & \;\;\,6} + \pmatrix{\;\;\,0 & 4 \\ -2 & 5} = \pmatrix{2 & \;\,3 \\ 1 & 11}$
(iii). $\pmatrix{\;\;\,0 & 4 \\ -2 & 5} + \pmatrix{2 & -1 \\ 3 & \;\;\,6} = \pmatrix{2 & \;\,3 \\ 1 & 11}$
End of Example 53.2. Matrix subtraction
- Two matrices $A$ and $B$ can be subtracted if and only if they are of the same size.
- To form $A - B$ subtract each element of $B$ from the corresponding element of $A$.
- The result of the subtraction is a matrix of the same size.
- As for subtraction of real numbers, matrix subtraction is not commutative, i.e. $A - B \neq B - A$, see the next example.
Example 6
In the following carry out the specified subtraction.
(i). $\pmatrix{3 & 1 & -2 \\ 4 & 0 & \;\;\,8} - \pmatrix{2 & -3 & -1 \\ 2 & -5 & \;\;\,1} = \pmatrix{1 & 4 & -1 \\ 2 & 5 & \;\;\,7}$
(ii). $\pmatrix{2 & -3 & -1 \\ 2 & -5 & \;\;\,1} - \pmatrix{3 & 1 & -2 \\ 4 & 0 & \;\;\,8} = \pmatrix{-1 & -4 & \;\;\,1 \\ -2 & -5 & -7}$
End of Example 63.3. Scalar multiplication of a matrix
- Any matrix can be multiplied by a number (scalar) and this procedure is referred to as scalar multiplication.
- Scalar multiplication is performed by multiplying each element in the matrix by the number.
- Scalar multiplication must not be confused with matrix multiplication which will be defined later.
Example 7
Simplify each of the following by performing the scalar multiplication.
(i). $2\pmatrix{0 & \;\;\,4 \\1 & -1} = \pmatrix{0 & \;\;\,8 \\ 2 & -2}$
(ii). $-0.1\pmatrix{-3 \\ -2 \\ \;\;\,0 \\ \;\;\,2} = \pmatrix{\;\;0.3 \\ \;\;0.2 \\ \;\;\;\;0 \\ -0.2}$
End of Example 7Example 8
Let $A = \pmatrix{1 & 1 & 2 \\ 2 & 3 & 4}, B = \pmatrix{0 & -1 & \;\;\,0 \\ 1 & \;\;\,0 & -1}$ and $C = \pmatrix{\;\;\,1 & 0 \\ -9 & 4}$
If possible simplify each of the following:
(i). $2A + 3B$, (ii). $3B - 2A$(iii). $C - A$
Solution
(i). $2A + 3B = 2\pmatrix{1 & 1 & 2 \\ 2 & 3 & 4} + 3\pmatrix{0 & -1 & \;\;\,0 \\ 1 & \;\;\,0 & -1}$
$=\; \pmatrix{2 & 2 & 4 \\ 4 & 6 & 8} + \pmatrix{0 & -3 & \;\;\,0 \\ 3 & \;\;\,0 & -3}$
$=\; \pmatrix{2 & -1 & 4 \\ 7 & \;\;\,6 & 5}$
(ii). $3B - 2A = 3\pmatrix{0 & -1 & \;\;\,0 \\ 1 & \;\;\,0 & -1} - 2\pmatrix{1 & 1 & 2 \\ 2 & 3 & 4}$
$=\; \pmatrix{0 & -3 & \;\;\,0 \\ 3 & \;\;\,0 & -3} - \pmatrix{2 & 2 & 4 \\ 4 & 6 & 8}$
$=\; \pmatrix{-2 & -5 & \;\;-4 \\ -1 & -6 & -11}$
(iii). We are unable to calculate $C - A$ as the matrices have different sizes.
Here $C$ is a $2 \times 2$ matrix while $A$ is a $2 \times 3$ matrix.
End of Example 8Now watch the following:
📹 Addition, subtraction and scalar multiplication of matrices
3.4. Matrix Multiplication
- Matrix multiplication can only be carried out between matrices which are conformable for matrix multiplication.
- Two matrices $A$ and $B$, with sizes $m \times n$ and $p \times q$ respectively, are conformable for multiplication, $A \times B$, if and only if $n = p$ ; i.e the number of columns of $A$ is the same as the number of rows of $B$.
- The result of multiplying a $m \times n$ matrix, $A$, (on the left) and an $p \times q$ matrix, $B$, (on the right) where $n = p$, is a $m \times q$ matrix and we write the product as $AB$.
- Note that matrix multiplication may be defined for $AB$ but not necessarily for $BA$. Hence, matrix multiplication is not in general commutative.
Note: If the “inner dimensions” $n$ and $p$ are equal we can multiply the matrices and the resulting product matrix has size given by the “outer dimensions”, i.e. $m \times q$.
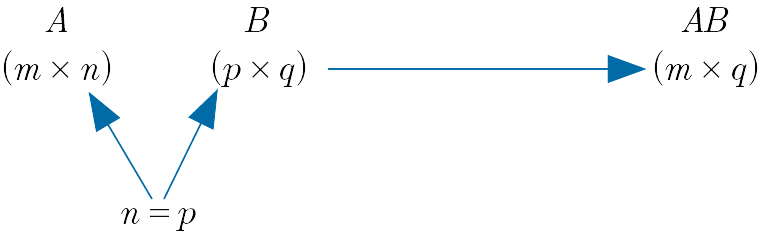
If required further resources on multiplication of matrices can be found at:
📹 Matrix Multiplication 1 (Exam Solutions)
📹 Matrix Multiplication 2 (Khan Academy)
🔗 Matrix Multiplication 3 (Mathcentre)
Example 9
Determine which of the following matrices are conformable for matrix multiplication
$A = \pmatrix{1 & \;\;\,2 & 3 \\ 4 & -5 & 6}, B = \pmatrix{1 & 2 \\ 3 & 4}, C = \pmatrix{1 & \;\;\,2 \\ 2 & \;\;\,4 \\ 3 & -1}$.
Solution
The matrix $A$ is $2 \times 3$.
The matrix $B$ is $2 \times 2$.
The matrix $C$ is $3 \times 2$.
(i). First consider the matrix product $AB$.
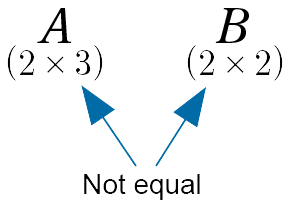
The “inner dimensions” are not equal and so we cannot perform the matrix multiplication. The number of columns in $A(3)$ does not equal the number of rows in $B( 2)$.
(ii). Now consider the matrix product $AC$.
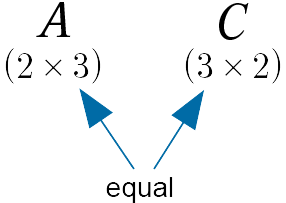
The “inner dimensions” are equal and so we can perform the matrix multiplication and the product matrix will have size given by the “outer dimensions”, i.e. $2 \times 2$.
Exercise: Confirm the following: $BA, AC, CA, CB$ and $BB$ are valid multiplications; whereas we cannot calculate $AB, BC, AA$ or $CC$.
End of Example 93.4.1. Matrix multiplication and the scalar (dot) product
To multiply two matrices, conformable for matrix multiplication, involves an extension of the scalar (dot) product procedure from vector algebra.
To form the result of multiplying $A$ (on the left) by $B$ (on the right) (i.e. to form the product $AB$) we view $A$ as a matrix composed of rows and $B$ as a matrix made up of columns.
The entries in the product matrix are determined by forming dot products.
To determine the element in Row $i /$ Column $j$, i.e. position $( i, j )$, of $AB$ we form the dot product of Row $i$ of matrix $A$ with Column $j$ of matrix $B$.
Example 10
Let $A = \pmatrix{\;\;\,1 & 6 & -2 \\ \;\;\,3 & 0 & \;\;\,3 \\ -2 & 3 & -1}$ and $B = \pmatrix{1 & \;\;\,2 \\ 1 & -2 \\ 3 & \;\;\,0}$
The product matrix $AB$ can be calculated as $A$ has size $3 \times 3$ and $B$ has size $3 \times 2$, i.e. the number of columns of $A$ is the same as the number of rows of $B$.
Hence, the product matrix, $AB$ will have size $3 \times 2$.
For example, to obtain the element in Row 1/Column 1, i.e. position $(1, 1)$ of $AB$ we take the dot product of Row 1 of $A$ with Column 1 of $B$, i.e.
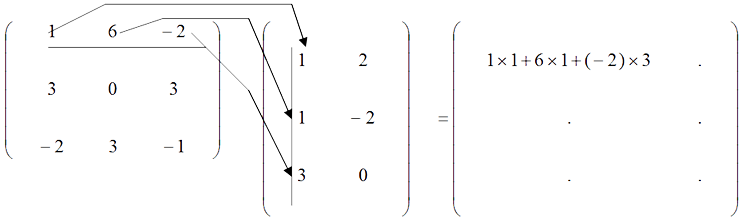
To obtain the element in Row 1/Column 2, i.e. position $(1, 2)$ we take the dot product of Row 1 of $A$ with Column 2 of $B$. In vector form we have,
$\pmatrix{1 & 6 & -2}. \pmatrix{\;\;\,2 \\ -2 \\ \;\;\,0} = 1 \times 2 + 6 \times (-2) + (-2) \times 0 = -10$.
This process can be continued to generate the 6 components of the $3 \times 2$ product matrix, $AB$.
$\pmatrix{\;\;\,1 & 6 & -2 \\ \;\;\,3 & 0 & \;\;\,3 \\ -2 & 3 & -1}\pmatrix{1 & \;\;\,2 \\ 1 & -2 \\3 & \;\;\,0} = \pmatrix{1 \times 1 + 6 \times 1 + (-2) \times 3 & 1 \times 2 + 6(-2) + (-2) \times 0 \\ 3 \times 1 + 0 \times 1 + 3 \times 3 & 3 \times 2 + 0 \times (-2) + 3 \times 0 \\ -2 \times 1 + 3 \times 1 + (-1) \times 3 & -2 \times 2 + 3 \times (-2) + (-1) \times 0}$
$= \pmatrix{\;\;\,1 & -10 \\ \;\;12 & \;\;\;\,6 \\ -2 & -10}$
End of Example 10Example 11
Let $A = \pmatrix{0 & \;\;\;4 \\ 1 & -1}$ and $B = \pmatrix{1 & \;\;\;1 \\ 2 & -1}$. If possible calculate $AB$ and $BA$.
Solution
In this case $A$ and $B$ are both $2 \times 2$ (square) matrices and so we can calculate $AB$ and $BA$. The result of both multiplications will be a $2 \times 2$ matrix. We have
$AB = \pmatrix{0 & \;\;\;4 \\ 1 & -1}\pmatrix{1 & \;\;\;1 \\ 2 & -1} = \pmatrix{\;\;\;8 & -4 \\ -1 & \;\;\;2}$
and
$BA = \pmatrix{1 & \;\;\;1 \\ 2 & -1}\pmatrix{0 & \;\;\;4 \\ 1 & -1} = \pmatrix{\;\;\;1 & 3 \\ -1 & 9}$
Note: This is an example of a very important result in matrix arithmetic. In general, for square matrices $A$ and $B$, we have that $AB \neq BA$.
End of Example 11Example 12
If possible evaluate the following matrix products:
(i). $\pmatrix{\;\;\,1 & 2 & \;\;\,3 \\ \;\;\,2 & 0 & \;\;\,1 \\ -1 & 1 & -1}\pmatrix{\;\;\,1 & 2 \\ \;\;\,4 & 2 \\ -1 & 0}$.
(ii). $\pmatrix{a & b \\ b & a}\pmatrix{1 & 2 \\ 3 & 4}$.
(iii). $\pmatrix{1 & x \\ x & 2}\pmatrix{x & y \\ x & 1}$.
(iv). $\pmatrix{\;\;\,3 \\ -1 \\ \;\;\,2}\pmatrix{2 & 0 & -1 & 6}$
(v). $\pmatrix{2 & 0 & -1 & 6}\pmatrix{\;\;\,3 \\ -1 \\ \;\;\,2}$.
Solution
(i) $\pmatrix{\;\;\,1 & 2 & \;\;\,3 \\ \;\;\,2 & 0 & \;\;\,1 \\ -1 & 1 & -1}\pmatrix{\;\;\,1 & 2 \\ \;\;\,4 & 2 \\ -1 & 0}$.
The product can be formed as the first matrix has size $3 \times 3$ and the second matrix has size $3 \times 2$, i.e. the number of columns in the first matrix $(3)$ is the same as the number of rows $(3)$ in the second matrix. The product matrix will have size $3 \times 2$. Multiplying gives,
$\pmatrix{1 \times 1 + 2 \times 4 + 3 \times (-1) & 1 \times 2 + 2 \times 2 + 3 \times 0 \\ 2 \times 1 + 0 \times 4 + 1 \times (-1) & 2 \times 2 + 0 \times 2 + 1 \times 0 \\-1 \times 1 + 1 \times 4 + (-1) \times (-1) & -1 \times 2 + 1 \times 2 + (-1) \times 0} = \pmatrix{6 & 6 \\ 1 & 4 \\ 4 & 0}$
(ii). $\pmatrix{a+3b & 2a+4b \\ b+3a & 2b+4a}$ (Exercise: Check this answer)
(iii). $\pmatrix{x + x^2 & y + x \\ x^2 + 2x & xy + 2}$ (Exercise: Check this answer)
(iv). $\pmatrix{\;\;\,3 \\ -1 \\ \;\;\,2}\pmatrix{2 & 0 & -1 & 6}$
The product can be formed as the first matrix has size $3 \times 1$ and the second matrix has size $1 \times 4$, i.e. the number of columns in the first matrix $(1)$ is the same as the number of rows $(1)$ in the second matrix. The product matrix will have size $3 \times 4$. Multiplying gives,
$\pmatrix{\;\;\,3 \times 2 & \;\;\,3 \times 0 & \;\;\,3 \times (-1) & \;\;\,3 \times 6 \\ -1 \times 2 & -1 \times 0 & -1 \times (-1) & -1 \times 6 \\ \;\;\,2 \times 2 & \;\;\,2 \times 0 & \;\;\,2 \times (-1) & \;\;\,2 \times 6} = \pmatrix{\;\;\,6 & 0 & -3 & \;\;16 \\ -2 & 0 & \;\;\,1 & -6 \\ \;\;\,4 & 0 & -2 & \;\;12}$
(v). $\pmatrix{2 & 0 & -1 & 6}\pmatrix{\;\;\,3 \\ -1 \\ \;\;\,2}$
The product cannot be formed as the first matrix has size $1 \times 4$ and the second matrix has size $3 \times 1$, i.e. the number of columns in the first matrix $(4)$ is not the same as the number of rows $(3)$ in the second matrix.
End of Example 12Example 13
Let $A = \pmatrix{1 & 2 & 3 \\ 2 & 5 & 3 \\ 1 & 0 & 8}$ and $B = \pmatrix{-40 & 16 & \;\;\,9 \\ \;\;\,13 & -5 & -3 \\ \;\;\;\;5 & -2 & -1}$. Calculate the matrix products $AB$ and $BA$.
Solution
(i). $AB = \pmatrix{1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1}, BA = \pmatrix{1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1}$.
Exercise: You should verify these calculations.
Unlike Example 11 we find that in this case matrix multiplication is commutative and $AB = BA$. This particular square matrix, with 1’s on the main diagonal (top left to bottom right) and 0’s everywhere else, is known as the identity matrix – see Sections 4.2 and 5 for further discussions.
End of Example 13Example 14
Determine the values of $x$ and $y$ that satisfy the following matrix equation.
$\pmatrix{1 & \;\;\,3 \\ x & -2}\pmatrix{2 & 4 \\ 3 & y} = \pmatrix{11 & \;\;\,1 \\ \;\;\,6 & 26}$
Solution
Expanding the left-hand-side (LHS) gives,
$\pmatrix{1 & \;\;\,3 \\ x & -2}\pmatrix{2 & 4 \\ 3 & y} = \pmatrix{11 & 4 + 3y \\ 2x - 6 & 4x - 2y} = \pmatrix{11 & \;\;\,1 \\ \;\;\,6 & 26}$
We therefore have three equations. The first two of these are equations in one variable which can easily be solved for $x$ and $y$. The third equation can be used to check our answers.
$ {\array{2x -6 = 6 \\ 4 + 3y = 1 \\ 4x - 2y = 26}}\Bigg\} \implies x = 6,\; y = -1 $.
End of Example 14 -
4. Special matrices
There are several special matrices that we should be aware of as they will be needed in future calculations.
4.1. Transpose Matrix
The matrix obtained from $A$ by interchanging the rows and the columns of $A$ is called the transpose of $A$ and is denoted $A^T$. We refer to this matrix as, “$A$ transpose”.
Example 15
Let $A = \pmatrix{1 & -2 & 7 \\ 6 & \;\;\,0 & 5}$. Write down the matrix $A^T$.
Solution
The matrix $A^T$ is obtained by interchanging rows and columns of the matrix $A$. Hence,
$A^T = \pmatrix{\;\;\,1 & 6 \\ -2 & 0 \\ \;\;\,7 & 5}$.
Note that Row 1 of $A$ is Column 1 of $A^T$ and Row 2 of $A$ is Column 2 of $A^T$.
Alternatively, Column 1 of $A$ is Row 1 of $A^T$, etc.
End of Example 154.1.1. Properties of transpose matrices
$(A^T)^T = A$ the transpose of a transpose matrix equals the original matrix. $(AB)^T = B^TA^T$ the transpose of a matrix product equals the product of the transpose matrices, with the order of multiplication reversed. $(A + B)^T = A^T + B^T$ the transpose of a matrix sum equals the sum of the transpose matrices. $(k A)^T = kA^T$ the transpose of a matrix multiplied by a scalar equals the scalar multiplied by the transpose of the matrix, $k \neq 0$ is a scalar 4.2. The identity matrix
We know that when any number in multiplied by the number 1 the value of the original number is unchanged, e.g. $1 \times 9 = 9,\;\; 1 \times 100 = 100$, etc.
In this context we call 1 the identity element for multiplication.
We now define an identity element for matrix multiplication so that when a matrix is multiplied by the identity it remains unchanged. This identity element is called an identity matrix and is only defined for square matrices. Although there is only a single multiplicative identity, i.e. 1, when working with numbers there are many different identity matrices depending on the size of the matrix in question, e.g. $2 \times 2,\;\; 3 \times 3$, etc.
The identity matrix has 1 on the main diagonal (the diagonal starting at top left and going to bottom right) and zeros everywhere else – see Example 13. The matrix is usually represented by $I$. Note that some textbooks include a subscript $n$, and write $I_n$, to indicate the size of the identity matrix.
Example 16
(i). The $2 \times 2$ identity matrix is, $I = \pmatrix{1 & 0 \\ 0 & 1}$.
(ii). We met the $3 \times 3$ identity matrix, $I = \pmatrix{1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1}$ in Example 13.
End of Example 164.3. The zero matrix
The zero matrix is a matrix for which every element is zero. Strictly speaking there are many zero matrices, one for each possible size of matrix. Here are the $2 \times 2$ and $2 \times 4$ zero matrices.
$\pmatrix{0 & 0 \\ 0 & 0}$$\pmatrix{0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0}$
The zero matrix is the identity matrix for matrix addition as shown in the following example.
Example 17
If $A = \pmatrix{\;\;\,1 & 9 \\ -2 & 3}$ then
$\pmatrix{\;\;\,1 & 9 \\ -2 & 3} + \pmatrix{0 & 0 \\ 0 & 0} = \pmatrix{\;\;\,1 & 9 \\ -2 & 3}$
The matrix $A$ is unchanged by addition of the zero matrix.
End of Example 174.4. Diagonal matrices
A square matrix is called a diagonal matrix if all the entries that do not lie on the main diagonal are zero. Note that it is allowed for some entries on the main diagonal to equal zero.
Example 18
The following matrices are all examples of diagonal matrices:
(i). $\pmatrix{6 & \;\;\,0 \\ 0 & -1} $ (ii). $\pmatrix{2 & \;\;\,0 & 0 \\ 0 & -5 & 0 \\0 & \;\;\,0 & 3}$(iii). $\pmatrix{4 & 0 & \;\;\,0 \\ 0 & 0 & \;\;\,0 \\0 & 0 & -1}$.
The identity matrix is a special case of a diagonal matrix where all the diagonal entries are equal to 1.
End of Example 184.5. Upper and lower triangular matrices
An upper triangular matrix is a square matrix in which all the entries below the main diagonal are zeros. Note that some entries on the main diagonal and/or above the main diagonal can equal zero.
Example 19
The matrices below are all examples of upper triangular matrices :
(i). $\pmatrix{6 & \;\;2 \\ 0 & -1}$ (ii). $\pmatrix{2 & -5 & 4 \\ 0 & \;\;9 & 6 \\ 0 & \;\;0 & 3}$(iii). $\pmatrix{4 & 2 & \;\;0 \\ 0 & 0 & \;\;3 \\ 0 & 0 & -1}$.
End of Example 19A lower triangular matrix is a square matrix in which all the entries above the main diagonal are zeros. Note that some entries on the main diagonal and/or below the main diagonal can equal zero.
Example 20
The matrices below are all examples of lower triangular matrices :
(i). $\pmatrix{6 & \;\;0 \\ 2 & -1}$ (ii). $\pmatrix{2 & \;\;0 & 0 \\ 6 & \;\;9 & 0 \\ 4 & -5 & 3}$(iii). $\pmatrix{4 & 0 & 0 \\ 3 & 1 & 0 \\ 2 & 0 & 0}$.
End of Example 204.6. Symmetric matrices
A square matrix is called a symmetric matrix if it is equal to its own transpose, i.e. $A = A^T$.
Example 21
The following matrices are all symmetric,
(i). $\pmatrix{\;\;\,3 & -1 \\ -1 & \;\;\,3}$ (ii). $\pmatrix{2 & \;\;\,0 & 1 \\ 0 & -6 & 3 \\ 1 & \;\;\,3 & 5}$(iii). $\pmatrix{3 & \;\;\,2 & \;\;\,1 \\ 2 & -9 & -3 \\ 1 & -3 & \;\;\,4}$
End of Example 21You are now ready to attempt the multiple choice exercise at the link below.
In the next section we look at how to calculate the determinant and inverse ( if it exists ) of a $2 \times 2$ matrix.
-
5. The determinant and inverse of a $2 × 2$ matrix
Consider the following arithmetic evaluations for numbers,
$ \matrix{2 \times 2^{-1}=2^{-1} \times 2 = 1 \\ 3 \times 3^{-1} = 3^{-1} \times 3 = 1 \\ 4 \times 4^{-1} = 4^{-1} \times 4 = 1 \\ ......................\\ ...................... \\ a \times a^{-1} = a^{-1} \times a = 1 \\ ..................... \\ ......................}$
One way of interpreting the above is that any (non-zero) number $a$ has associated with it a multiplicative inverse $a^{-1}$. Furthermore, any number multiplied by its inverse equals 1, the multiplicative identity for scalars.
We can make an analogous statement for (some) square matrices that will prove useful later.
For a general $2 \times 2$ matrix, $A = \pmatrix{a & b \\ c & d}$ provided
$det(A) = ad - bc \neq 0$
there exists another $2 \times 2$ matrix, called the inverse of $A$, denoted $A^{-1}$, where
$A^{-1} = {\Large\frac{1}{det(A)}}\pmatrix{\;\;\,d & -b \\ -c & \;\;\,a}$.
The quantity $det(A)$ is called the determinant of $A$ and is often written, $\mid A \mid$ .
The determinant of a matrix can therefore be used to determine the existence (or otherwise) of a matrix inverse by checking that it is non-zero.
In a manner similar to that observed earlier for scalars,
$AA^{-1} = A^{-1}A = I$
where $I$ is the identity matrix with the same size as the square matrix $A$. Also,
$AI = IA = A$.
Note that $A^{-1}$ must not be interpreted as ${\Large\frac{1}{A}}$.
A matrix with an inverse is called invertible or non-singular.
A matrix with no inverse is said to be non-invertible or singular.
We now look at how to determine inverse matrices, where they exist, for the $2 \times 2$ case.
Example 22
Calculate the determinant of each of the following matrices. Hence, identify which matrices are invertible and for each invertible matrix calculate its inverse.
(i). $A = \pmatrix{\;\;\,2 & -1 \\ -2 & \;\;\,1}$ (ii). $B = \pmatrix{7 & 3 \\ 2 & 1}$
(iii). $C = \pmatrix{0 & 1 \\ 0 & 1}$ (iv). $M = \pmatrix{\;\;\,2 & \;\;\,0 \\ -2 & -3}$
Solution
(i). $det(A) = 2 \times 1 - (-1) \times (-2) = 2 - 2 = 0$. No Inverse.
(ii). $det(B) = 7 \times 1 - 3 \times 2 = 7 - 6 = 1 \neq 0$. Matrix has an inverse.
$B^{-1} = \ {\Large\frac{1}{1}}\pmatrix{\;\;\,1 & -3 \\ -2 & \;\;\,7} =\pmatrix{\;\;\,1 & -3 \\ -2 & \;\;\,7}$
Exercise: Check that $BB^{-1} = B^{-1}B = I$ .
(iii). $det(C) = 0 \times 1 - 1 \times 0 = 0 - 0 = 0$. No inverse.
(iv). $det(M) = 2 \times (-3) - 0 \times (-2) = -6 \neq 0$.
$M^{-1} = -{\Large\frac{1}{6}}\pmatrix{-3 & 0 \\ \;\;\,2 & 2}$
$= {\Large\frac{1}{6}}\pmatrix{\;\;\,3 & \;\;\,0 \\ -2 & -2}$
Exercise: Check that $MM^{-1} = M^{-1}M = I$.
End of Example 22Now watch the following:
📹 Inverse of a $2 \times 2$ matrix
5.1. Properties of inverse matrices
If $A$ and $B$ are invertible matrices:
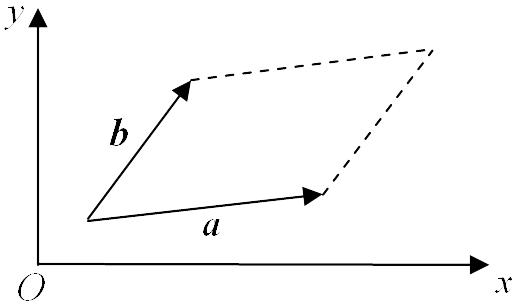
$(A^{-1})^{-1} = A$ the inverse of an inverse matrix equals the original matrix. $(AB)^{-1} = B^{-1}A^{-1}$ the inverse of a matrix product equals the product of the inverse matrices, with the order of multiplication reversed. $(kA)^{-1} = {\Large\frac{1}{k}}A^{-1}$ the inverse of a matrix multiplied by a scalar equals the inverse of the scalar multiplied by the inverse of the matrix, $k \neq 0$ is a scalar. $(A^T)^{-1} = (A^{-1})^T$ the inverse of a transpose matrix equals the transpose of the inverse matrix. Aside: Geometrically, the absolute value of the determinant of a $2 \times 2$ matrix $A = \pmatrix{a & b \\ c & d}$ is the area of a parallelogram whose edges are the vectors $\boldsymbol{a} = (a,b)$ and $\boldsymbol{b} = (c,d)$.
In the next section we look at how to calculate the determinant and inverse of a $3 \times 3$ matrix.
-
6. The determinant and inverse of a $3 \times 3$ matrix
There are a number of techniques available for calculating the inverse of a $3 \times 3$ matrix. In our work we shall focus on the cofactor method. Before looking at finding the inverse of a $3 \times 3$ matrix, when it exists, we need to know how to calculate the determinant of the matrix.
6.1. The determinant a $3 \times 3$ matrix
Here we look at two methods for calculating the determinant of a $3 \times 3$ matrix,
$A = \pmatrix{a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}}$.
6.1.1. Evaluating the determinant by cofactor expansion
To apply this method we need to know how to calculate minors and cofactors.
Consider a typical element, $a_{ij}$, of the $3 \times 3$ matrix, $A$, given above.
- The minor of element, $a_{ij}$ , denoted by $M_{ij}$ , is obtained as follows :
- remove the $i^{\text{th}}$ row from $A$.
- remove the $j^{\text{th}}$ row from $A$.
- the minor $M_{ij}$ is the determinant of the remaining $2 \times 2$ submatrix.
The cofactor, $C_{ij}$, for element $a_{ij}$ is obtained by multiplying the minor of $a_{ij}$ by $(-1)^{i + j}$, so that $C_{ij} = (-1)^{i + j}M_{ij}$.
We note here that $C_{ij} = M_{ij}$ if $i + j$ is even and $C_{ij} = -M_{ij}$ if $i + j$ is odd.
To obtain the determinant of the matrix $A$ we select a row (column), multiply each entry in the chosen row (column) by its cofactor and sum the resulting values.
For example, if we expand on row $k$ we have:
$$\text{det}(A) = a_{k1}C_{k1} + a_{k2}C_{k2} + a_{k3}C_{k3} = \sum_{j = 1}^{3} a_{kj}C_{kj}.$$
Alternatively, if we expand on column $k$ we have
$$\text{det}(A) = a_{1k}C_{1k} + a_{2k}C_{2k} + a_{3k}C_{3k} = \sum_{j = 1}^{3} a_{jk}C_{jk}.$$
We illustrate the process with an example.
Example 23
Calculate the determinant of the matrix, $A = \pmatrix{3 & \;\;\,2 & -1 \\ 1 & \;\;\,6 & \;\;\,3 \\ 2 & -4 & \;\;\,0}$ using cofactor expansion.
Solution
- We choose to expand along Row 1 and first calculate the minor for each entry :
- the minor of entry $a_{11} = 3$ is:
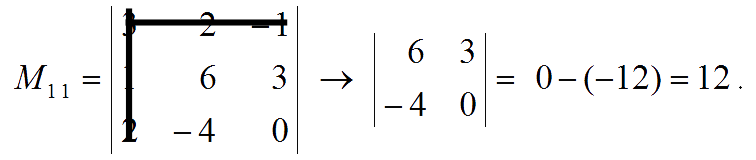
- the minor of entry $a_{12} = 2$ is:
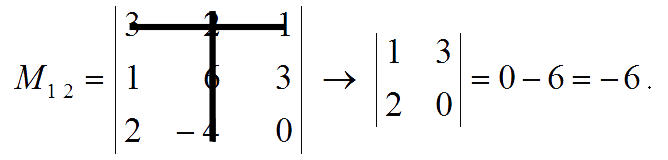
- the minor of entry $a_{13} = -1$ is:
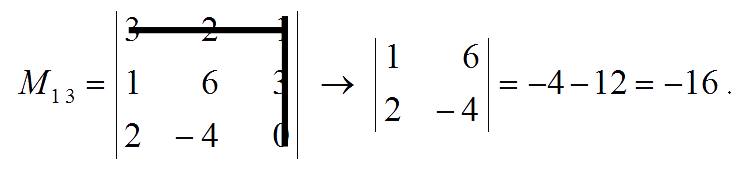
- Now calculate the cofactors :
- the cofactor of entry $a_{11}$ is: $C_{11} = (-1)^{1 + 1} \times M_{11} = (-1)^2 \times 12 = 12$.
- the cofactor of entry $a_{12}$ is: $C_{12} = (-1)^{1 + 2} \times M_{12} = (-1)^3 \times (-6) = 6$.
- the cofactor of entry $a_{13}$ is: $C_{13} = (-1)^{1 + 3} \times M_{13} = (-1)^4 \times (-16) = -16$.
Finally, multiply each entry in Row 1 by its cofactor and sum the values. Hence,
$$\text{det}(A) = \sum_{j = 1}^{3}a_{1j}C_{1j}$$
$= a_{11}C_{11} + a_{12}C_{12} + a_{13}C_{13}$
$= 3 \times 12 + 2 \times 6 + (-1) \times (-16)$
$= 36 + 12 + 16$
$=$ $64$.
Notes
(i). The value of the determinant will be the same regardless of which row or column we expand on.
(ii). When calculating the determinant of a matrix we expand along the row or column containing the most zeros in order to minimise the arithmetic.
End of Example 23The process described above can be presented in a more compact form by making use of the sign array,
$$\pmatrix{+ & - & + \\ - & + & - \\ + & - & +}$$
to associate a sign with each entry in our matrix. This approach eliminates the need to calculate the cofactors explicitly. We illustrate the method by repeating Example 23 to (hopefully) obtain the same value as above for the determinant of the matrix $A$.
Example 24
Calculate the determinant of the matrix, $A = \pmatrix{3 & \;\;\,2 & -1 \\1 & \;\;\,6 & \;\;\,3 \\ 2 & -4 & \;\;\,0}$ by expanding on Row 1. Repeat the calculation by expanding on Column 2.
Solution
Expand along the first row of $A$ calculating the minors. Multiply each minor by the corresponding entry from the matrix $A$, augmented by the appropriate sign from the first row of the sign array, i.e. $(+ \;\; - \;\; +)$ and sum the results.
$\text{det}(A) = + 3. \bigg |\matrix{\;\;\,6 & 3 \\ -4 & 0}\bigg | - 2. \bigg |\matrix{1 & 3 \\ 2 & 0} \bigg | + (-1). \bigg |\matrix{1 & \;\;\,6 \\ 2 & -4}\bigg |$
$= 3.(6 \times 0 - 3 \times (-4)) - 2.(1 \times 0 - 3 \times 2) + (-1).(1 \times(-4) - 6 \times 2)$
$= 36 + 12 + 16$
$=$ $64$.
Now expand along the second column of $A$ using the appropriate signs from the second column of the sign array, i.e. $(- \;\; + \;\; -)$ :
$\text{det}(A) = -2. \bigg | \matrix{1 & 3 \\ 2 & 0} \bigg | + 6. \bigg | \matrix{3 & -1 \\ 2 & \;\;\, 0} \bigg | - (-4). \bigg | \matrix{3 & -1 \\ 1 & \;\;\, 3} \bigg |$
$= - 2.(1 \times 0 - 3 \times 2) + 6.(3 \times 0 - (-1) \times 2) + 4.(3 \times 3 - (-1) \times 1)$
$= 12 + 12 + 40$
$=$ $64$ as obtained earlier.
End of Example 24Now watch the following:
📹 Determinant of a 3x3 matrix Example (1)
📹 Determinant of a 3x3 matrix Example (2)
6.1.2. Evaluating the determinant by the Rule of Sarrus
An alternative approach for calculating the determinant of a $3 \times 3$ matrix
$A = \pmatrix{a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3}$
was developed by the French mathematician Pierre Sarrus (1798-1861). The Rule of Sarrus involves the following steps:
Rewrite the first two columns of the matrix to the right of it :
$${\LARGE\matrix{a_1 & a_2 & a_3 & a_1 & a_2 \\ b_1 & b_2 & b_3 & b_1 & b_2 \\ c_1 & c_2 & c_3 & c_1 & c_2}}$$
Using the left to right diagonals take the products $a_1b_2c_3, \; a_2b_3c_1, \; a_3b_1c_2$:
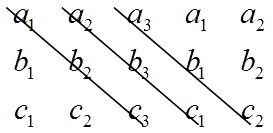
Using the right to left diagonals take the products $a_3b_2c_1, \; a_1b_3c_2, \;a_2b_1c_3$ :
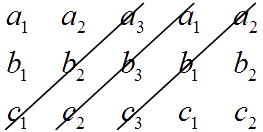
Combine the above and calculate the determinant as follows :
$\text{det}(A) = a_1b_2c_3 + a_2b_3c_1 + a_3b_1c_2 - a_3b_2c_1 - a_1b_3c_2 - a_2b_1c_3$.The Rule of Sarrus is essentially the same as the method we described previously.
Example 25
Calculate the determinant of the matrix, $A = \pmatrix{3 & \;\;\,2 & -1 \\ 1 & \;\;\,6 & \;\;\, 3 \\ 2 & -4 & \;\;\,0}$ using the Rule of Sarrus.
Solution
Rewrite the first two columns of the matrix to the right of it :
$\matrix{3 & \;\;\,2 & -1 & 3 & \;\;\,2 \\ 1 & \;\;\,6 & \;\;\,3 & 1 & \;\;\,6 \\ 2 & -4 &\;\;\,0 & 2 & -4}$Calculate the determinant as described above :
$\text{det}(A) = 3 \times 6 \times 0 + 2 \times 3 \times 2 + (-1) \times 1 \times (-4)$
$-\, 2 \times 1 \times 0 - 3 \times 3 \times (-4) - (-1) \times 6 \times 2$
$= 0 + 12 + 4 - 0 - (-36) - (-12)$
$=$ $64$.
Note that, as expected, this is the same answer as we obtained using the previous method.
Now watch the following:
Aside: Geometrically, the absolute value of the determinant of a $3 \times 3$ matrix is the volume of a parallelepiped whose edges are the vectors $\boldsymbol{u} = (a_1, \,a_2,\,a_3)$, $\boldsymbol{v} = (b_1,\,b_2,\,b_3)$ and $\boldsymbol{w} = (c_1, \,c_2,\,c_3)$.
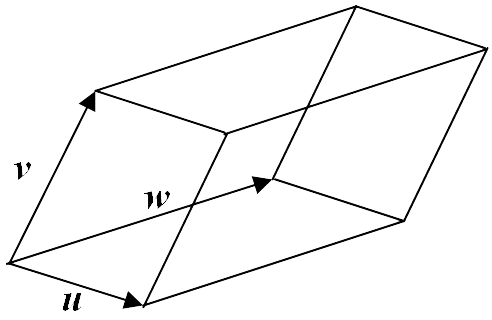 End of Example 25
End of Example 256.2. The inverse of a $3 \times 3$ matrix by the cofactor method
We now extend the idea of an inverse matrix to the $3 \times 3$ case. In general, the inverse of a matrix, $A$, is given by the formula :
$A^{-1} = \frac{1}{\det(A)}adj(A)$ $\text{det}(A) \neq 0$
where the matrix $adj(A)$ is known as the adjoint matrix of $A$.
In order to calculate the inverse of a matrix $A$, if it exists, we must therefore obtain the determinant of $A$ and the adjoint of $A$. The derivation of the adjoint matrix requires us to calculate the matrix of minors of $A$ and matrix of cofactors of $A$. The following paragraphs illustrate the methodology by way of an example reducing the procedure to five distinct steps.
Example 26
Determine the inverse of the matrix, $A = \pmatrix{3 & \;\;\, 2 & -1 \\ 1 & \;\;\, 6 & \;\;\, 3 \\ 2 & -4 & \;\;\, 0}$ , if it exists.
Solution
Although we have performed some of the calculations for this example previously for completeness we present a full solution.
STEP 1: Calculate the determinant of $A$
Expanding along the third row the determinant of $A$ is :
$\text{det}(A) = 2. \bigg | \matrix{2 & -1 \\ 6 & \;\;\, 3} \bigg | - (- 4) \bigg | \matrix{3 & -1 \\ 1 & \;\;\, 3} \bigg | + 0. \bigg | \matrix{3 & 2 \\ 1 & 6} \bigg | = 2 \times 12 + 4 \times 10 = 64$.
Since $\text{det}(A) \neq 0,\; A^{-1}$ exists.
STEP 2: Calculate the matrix of minors
- The minor of entry $a_{ij}$, denoted by $M_{ij}$, is obtained as follows:
- remove the $i^{\text{th}}$ row.
- remove the $j^{\text{th}}$ column.
- the minor $M_{ij}$ is the determinant of the remaining $2 \times 2$ submatrix.
The minor of entry $a_{11}$ is:
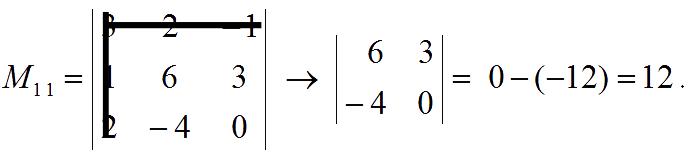
The minor of entry $a_{12}$ is:
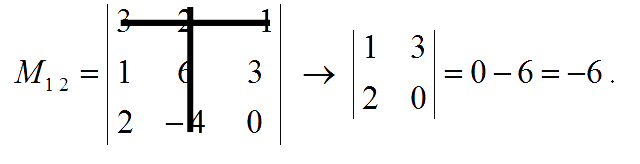
The minor of entry $a_{13}$ is:
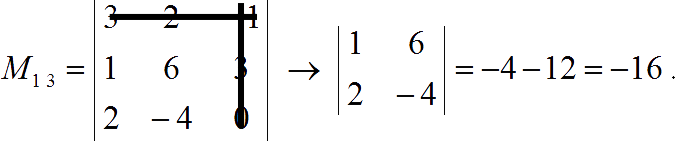
The minor of entry $a_{21}$ is:
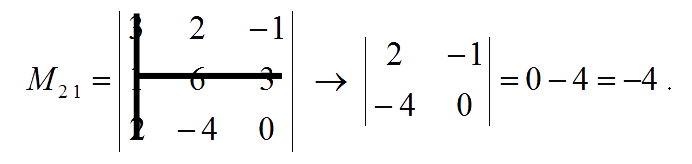
The minor of entry $a_{22}$ is:
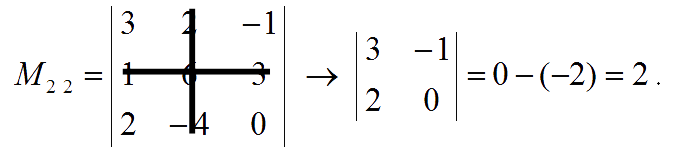
The minor of entry $a_{23}$ is:
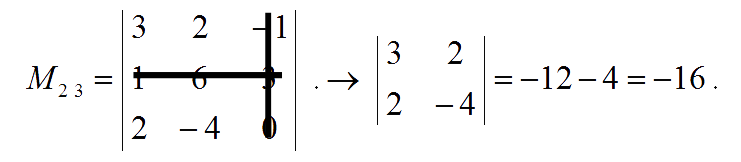
The minor of entry $a_{31}$ is:
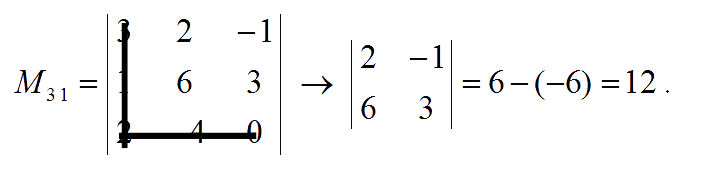
The minor of entry $a_{32}$ is:
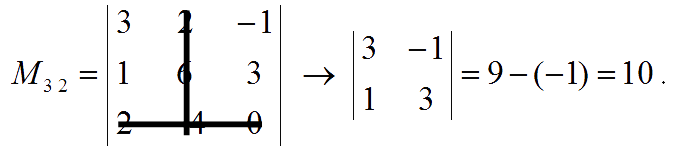
The minor of entry $a_{33}$ is:
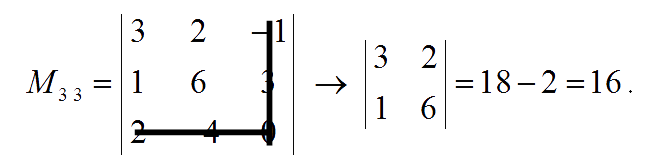
Hence, the matrix of minor is : $\pmatrix{\;\,12 & -6 & -16 \\-4 & \;\;\,2 & -16 \\ \;\,12 & \;\,10 & \;\;\, 16}$.
STEP 3: Calculate the cofactor matrix
The cofactor of entry $a_{ij}$, denoted by $C_{ij}$, is defined as $C_{ij} = (-1)^{i + j}M_{ij}$.
To obtain the cofactor matrix $cof(A)$ we use a shortcut and simply change signs of the elements of the matrix of minors, calculated in Step 2, using the sign matrix :
$\pmatrix{+ & - & + \\ - & + & - \\ + & - & +}$
Hence, we obtain the cofactor matrix :
$cof(A) = \pmatrix{12 & \;\;\,6 & -16 \\\;\,4 & \;\;\,2 & -16 \\ 12 & -10 & \;\;\, 16}$
STEP 4: Calculate the adjoint matrix
The adjoint of $A$ is defined to be the transpose of the cofactor matrix, i.e.
$adj(A) = \pmatrix{\;\;\,12 & \;\,4 & \;\;\,12 \\ \;\;\;6 & \;\,2 & -10 \\ -16 & 16 & \;\;\,16}$
STEP 5: Calculate the inverse matrix
The inverse of the matrix $A$ is calculated as :
$$A^{-1} = \frac{1}{\text{det}(A)}adj(A)$$
so that $A^{-1} = {\Large\frac{1}{64}} \pmatrix{\;\;\,12 & \;\,4 & \;\;12 \\ \;\;\;6 & \;\,2 & -10 \\-16 & 16 & \;\;16}$ which simplifies to give $A^{-1} = {\Large\frac{1}{32}} \pmatrix{\;\;\;6 & 2 & \;\;\;6 \\ \;\;\;3 & 1 & -5 \\ -8 & 8 & \;\;\;8}$ .
It is straightforward to check that $AA^{-1} = A^{-1}A = I$. We have,
$AA^{-1} = {\Large\frac{1}{32}}\pmatrix{3 & \;\;\;2 & -1 \\ 1 & \;\;\;6 & \;\;\;3 \\ 2 & -4 & \;\;\;0}\pmatrix{\;\;\;6 & 2 & \;\;\;6 \\ \;\;\;3 & 1 & -5 \\ -8 & 8 & \;\;\;8} = {\Large\frac{1}{32}}\pmatrix{32 & \;\;\,0 & \;\;\,0 \\ \;\;0 & 32 & \;\;0 \\ \;\;\,0 & \;\;\,0 & 32} = \pmatrix{1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1} = I$ as required.
End of Example 26Watch these videos in the given order :
📹 Inverse of a $3 \times 3$ matrix
Example 27
Determine the inverse of the matrix $A = \pmatrix{3 & -1 & 6 \\ 9 & -5 & 2 \\ 0 & \;\;\,4 & 7}$ if it exists.
Solution
STEP 1: Calculate the determinant of $A$
$\text{det}(A) = 3. \bigg | \matrix{-5 & 2 \\ \;\;\,4 & 7} \bigg | - (-1). \bigg | \matrix{9 & 2 \\0 & 7} \bigg | + 6. \bigg | \matrix{9 & -5 \\ 0 & \;\;\,4} \bigg | = 3 \times (-43) + 63 + 6 \times 36 = 150.$
Since $\text{det}(A) \neq 0,\; A^{-1}$ exists.
STEP 2: Calculate the matrix of minors
The minor of entry $a_{11}$ is:
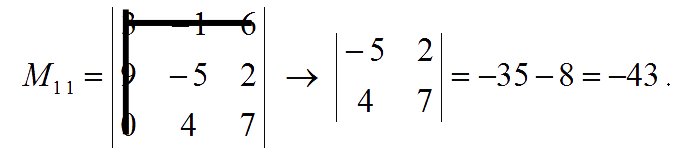
The minor of entry $a_{12}$ is:
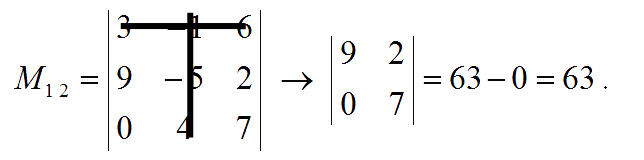
The minor of entry $a_{13}$ is:
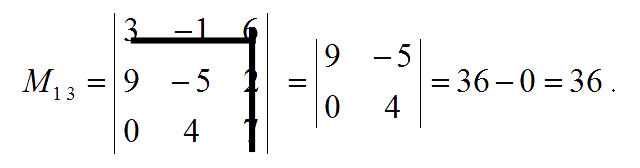
The minor of entry $a_{21}$ is:
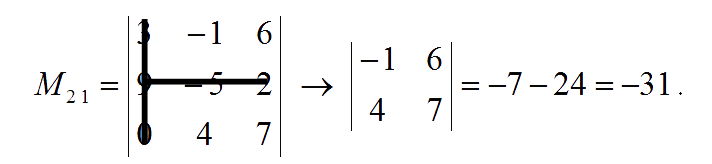
The minor of entry $a_{22}$ is:
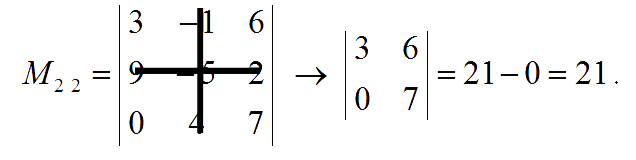
The minor of entry $a_{23}$ is:
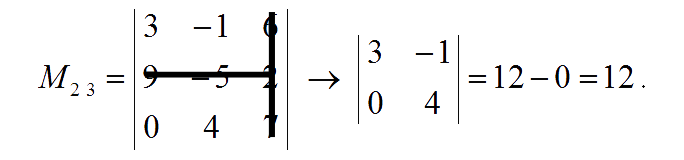
The minor of entry $a_{31}$ is:
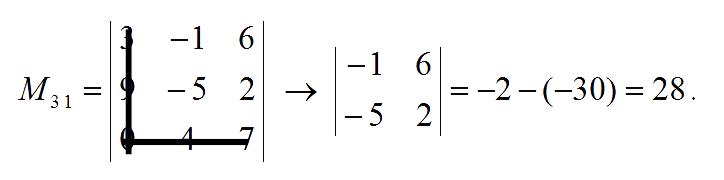
The minor of entry $a_{32}$ is:
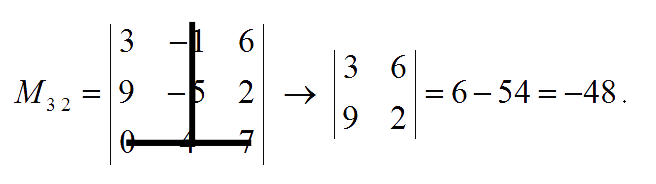
The minor of entry $a_{33}$ is:
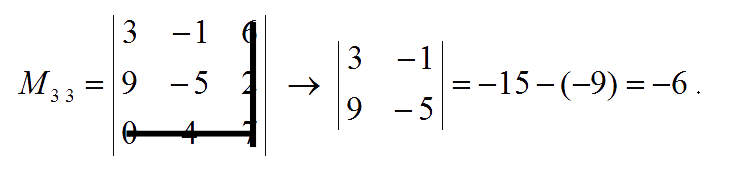
Hence, the matrix of minors is: $\pmatrix{-43 & \;\;63 & \;36 \\ -31 & \;\;21 & \;12 \\ \;\;\,28 & -48 & -6}$
STEP 3: Calculate the cofactor matrix
The cofactor of entry $a_{ij}$, denoted by $C_{ij}$, is defined as $C_{ij} = (-1)^{i+j}M_{ij}$.
To obtain the cofactor matrix $cof(A)$ we simply change signs of the elements of the matrix of minors in Step 2 using the sign matrix :
$\pmatrix{+ & - & + \\ - & + & - \\ + & - & +}$
Hence, we obtain the cofactor matrix :
$cof(A) = \pmatrix{-43 & -63 & \;\;36 \\ \;\;\,31 & \;\;\,21 & -12 \\ \;\;\,28 & \;\;\,48 & \;-6}$.
STEP 4: Calculate the adjoint matrix
The adjoint of $A$ is determined as the transpose of the cofactor matrix, i.e.
$adj(A) = \pmatrix{-43 & \;\;\;31 & \;28 \\ -63 & \;\;\;21 & \;48 \\ \;\;\;36 & -12 & -6}$
STEP 5: Calculate the inverse matrix
The inverse of the matrix $A$ is calculated as
$A^{-1} = {\Large\frac{1}{\text{det}(A)}}adj(A)$
so that $A^{-1} = {\Large\frac{1}{150}}\pmatrix{-43 & \;\;\;31 & \;28 \\ -63 & \;\;\;21 & \;48 \\ \;\;\;36 & -12 & -6}$.
Check the inverse is correct as follows :
$AA^{-1} = {\Large\frac{1}{150}} \pmatrix{3 & -1 & 6 \\ 9 & -5 & 2 \\ 0 & \;\;\;4 & 7} \pmatrix{-43 & \;\;\;31 & \;28 \\ -63 & \;\;\;21 & \;48 \\ \;\;\;36 & -12 & -6} = {\Large\frac{1}{150}}\pmatrix{150 & 0 & 0 \\ 0 & 150 & 0 \\ 0 & 0 & 150} = \pmatrix{1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1} = I$ as required.
End of Example 27Example 28
Calculate the determinant of the matrix, $A = \pmatrix{1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9}$ and find $A^{-1}$ if it exists.
Solution
As an alternative we use the Rule of Sarrus to calculate the determinant. Writing
$\matrix{1 & 2 & 3 & 1 & 2 \\ 4 & 5 & 6 & 4 & 5 \\ 7 & 8 & 9 & 7 & 8}$
$\text{det}(A) = 1 \times 5 \times 9 + 2 \times 6 \times 7 + 3 \times 4 \times 8 - 2 \times 4 \times 9 - 1 \times 6 \times 8 - 3 \times 5 \times 7$
$= 45 + 84 + 96 - 72 - 48 - 105 = 225 - 225 = 0$.
As $\text{det}(A) = 0$ the matrix $A$ is not invertible.
Aside: Geometrically the result that $\det(A) = 0$ means that the vectors $(1, 2, 3)$, $(4, 5, 6)$, and $(7, 8, 9)$ are coplanar, i.e. they lie in the same plane.
End of Example 28 -
7. Solving systems of linear equations by matrix methods
In the past we have solved systems of linear equations (simultaneous equations) using methods such as elimination and substitution. As systems increase in size these methods quickly become difficult to apply and it is considerably more efficient to use matrices to obtain a solution. There are several matrix methods available, including Gaussian elimination, but we shall focus our interest on using the inverse matrix to solve systems of equations.
In dealing with simultaneous equations, we normally require as many equations as there are unknowns, e.g. 2 equations in 2 unknowns, 3 equations in 3 unknowns, and so on. For example, a system of $n$ equations in $n$ unknowns is given by :
$a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n = b_1 \\ a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n = b_2 \\ ............................... \\ ............................... \\ a_{n1}x_1 + a_{n2}x_2 + \cdots + a_{nn}x_{n} = b_n$
This system can be written as a matrix equation of the form
$A\boldsymbol{x} = \boldsymbol{b}$
- where
- $\boldsymbol{x}$ is a column vector $(n \times 1 )$ whose components are the unknowns in the equations.
- $A$ is a square matrix $(n \times n )$ whose elements are the coefficients of the unknowns.
- $\boldsymbol{b}$ is a column vector $(n \times 1 )$ of the equation constants, i.e. the right-hand-side values.
We therefore have
$A = \pmatrix{a_{11} & a_{12} & \cdots & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & \cdots & a_{2n} \\ \vdots & & \ddots & & \vdots \\ \vdots & & &\ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & \cdots & a_{nn}}$, $\boldsymbol{x} = \pmatrix{x_1 \\ x_2 \\ \vdots \\ \vdots \\ x_n}$, $\boldsymbol{b} = \pmatrix{b_1 \\ b_2 \\ \vdots \\ \vdots \\ b_n }$.
Provided $A$ is invertible, i.e. $\text{det}(A) \neq 0$ , the system has a unique solution.
The solution of the matrix equation is the vector $\boldsymbol{x}$ and the elements of $\boldsymbol{x}$ give the solution of the simultaneous equations.
To find $\boldsymbol{x}$, provided the coefficient matrix $A$ is invertible, we pre-multiply both sides of the matrix equation by the inverse of $A$ and simplify. We have
$A\boldsymbol{x} = \boldsymbol{b}$
$A^{-1}A\boldsymbol{x} = A^{-1}\boldsymbol{b}$
$I\boldsymbol{x} = A^{-1}\boldsymbol{b}$
$\boldsymbol{x} = A^{-1}\boldsymbol{b}$.
For comparison, an analogous procedure for a scalar equation is given below.
$ax = b$
$a^{-1}ax = a^{-1}b$
$1x = a^{-1}b$
$x = a^{-1}b$.
Now watch the following:
📹 Solving simultaneous equations – matrix methods:
Example 29
(i). Solve the system of equations
$x + 2y = - 1$
$4x - 3y = 18$
using the inverse matrix method.
Solution
First write the equations in the matrix form, $A\boldsymbol{x} = \boldsymbol{b}$ :
$\pmatrix{1 & \;\;\,2 \\ 4 & -3} \pmatrix{x \\ y} = \pmatrix{-1 \\ \;18} \\ \;\;\;\;\;\;\; A \;\;\;\;\;\;\;\;\;\, \boldsymbol{x} \;\;\;=\;\;\;\;\; \boldsymbol{b}$
Calculate $A^{-1}$ if it exists.
$\text{det}(A) = 1 \times (-3) - 2 \times 4 = - 11 \neq 0$ and so the matrix is invertible.
Hence,
$A^{-1} = - {\Large\frac{1}{11}}\pmatrix{-3 & -2 \\ -4 & \;\;\;1} = {\Large\frac{1}{11}} \pmatrix{3 & \;\;\;2 \\ 4 & -1}$.
Now solve the system by forming, $\boldsymbol{x} = A^{-1} \boldsymbol{b}$:
$\pmatrix{x \\ y} = {\Large\frac{1}{11}} \pmatrix{3 & \;\;\;2 \\ 4 & -1}\pmatrix{-1 \\ \;18} = {\Large\frac{1}{11}} \pmatrix{\;\;\,33 \\ -22} = \pmatrix{\;\;\,3 \\ -2} \\ \\ \;\;\boldsymbol{x} \;\;\; = \;\;\;\;\;\;\;\;\;\;\;A^{-1}\;\;\;\;\;\;\;\; \boldsymbol{b}$
Hence, $x = 3$ and $y = -2$.
(ii). Solve the system of equations
$4x + 2y = 10$
$3x - 7y = -1$
using the inverse matrix method.
Solution
First write the equations in the matrix form, $A \boldsymbol{x} = \boldsymbol{b}$ :
$\pmatrix{4 & \;\;\;2 \\ 3 & -7} \pmatrix{x \\ y} = \pmatrix{\;10 \\ -1}$.
Calculate $A^{-1}$ if it exists.
$\det(A) = -28 - 6 = - 34 \neq 0$ and so the matrix is invertible.
Hence,
$A^{-1} = - {\Large\frac{1}{34}}\pmatrix{-7 & -2 \\ -3 & \;\;\;4} = {\Large\frac{1}{34}} \pmatrix{7 & \;\;\;2 \\ 3 & -4}$.
Now solve the system by forming, $\boldsymbol{x} = A^{-1} \boldsymbol{b}$:
$\pmatrix{x \\ y} = {\Large\frac{1}{34}} \pmatrix{7 & \;\;\;2 \\ 3 & -4} \pmatrix{\;10 \\ -1} = {\Large\frac{1}{34}} \pmatrix{68 \\ 34} = \pmatrix{2 \\ 1}$.
Hence, $x = 2$ and $y = 1$.
(iii). Solve the system of equations given by
$3x + 2y - \;\;z = \;\;\;3$
$\;\;x + 6y + 3z = \;\;29$.
$2x - 4y \;\;\;\;\;\;\;\;= -18$
using the inverse matrix method.
Solution
In matrix form, $A \boldsymbol{x} = \boldsymbol{b}$, we have
$\pmatrix{3 &\;\;\; 2 & -1 \\ 1 & \;\;\;6 & \;\;\;3 \\ 2 & -4 & \;\;\;0} \pmatrix{x \\ y \\ z} = \pmatrix{\;\;\;3 \\ \;\;29 \\ -18}$.
We found the inverse of $A$ in Example 26, $A^{-1} = {\Large\frac{1}{32}} \pmatrix{\;\;\;6 & 2 & \;\;\;6 \\ \;\;\;3 & 1 & -5 \\ -8 & 8 & \;\;\; 8}$.
Now solve the system by forming, $\boldsymbol{x} = A^{-1} \boldsymbol{b}$ :
$\pmatrix{x \\ y \\ z} = {\Large\frac{1}{32}} \pmatrix{\;\;\; 6 & 2 & \;\;\;6 \\ \;\;\;3 & 1 & -5 \\ -8 & 8 & \;\;\;8} \pmatrix{\;\;\;\,3 \\ \;\;29 \\ -18} = {\Large\frac{1}{32}} \pmatrix{\;\;\;\,3 \\ \;\;29 \\ -18} = {\Large\frac{1}{32}} \pmatrix{-32 \\ \;128 \\ \;\;64} = \pmatrix{-1 \\ \;\;\; 4 \\ \;\;\; 2}$.
Hence, $x = -1$, $y = 4$ and $z = 2$.
End of Example 29Note: When the determinant of the coefficient matrix is non-zero, as in the above examples, the system will have a unique solution. If however, the determinant is close to zero this indicates that the matrix is almost singular (non-invertible) and we could run into numerical problems when calculating the inverse. When the determinant is zero the matrix does not have an inverse and the system has either no solution or infinitely many solutions. In such cases we must use an alternative method to solve the system such as Gaussian elimination.
-
Summary
- On completion of this unit you should be able to:
- perform basic matrix arithmetic including addition, subtraction and scalar multiplication.
- determine whether matrices are conformable for matrix multiplication and carry out matrix multiplication where appropriate.
- calculate the determinant and inverse (where it exists) for $2 \times 2$ and $3 \times 3$ matrices.
- apply matrix methods to solve systems of linear equations.