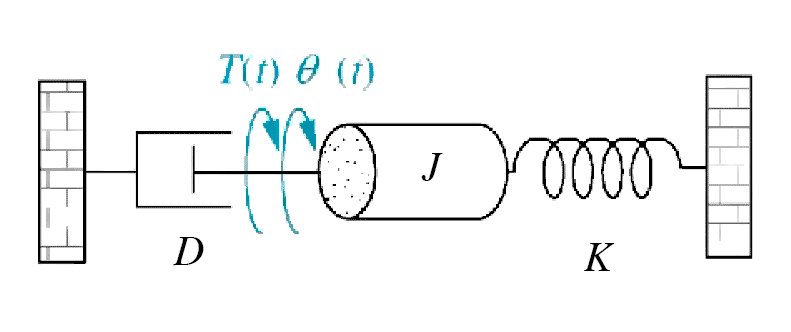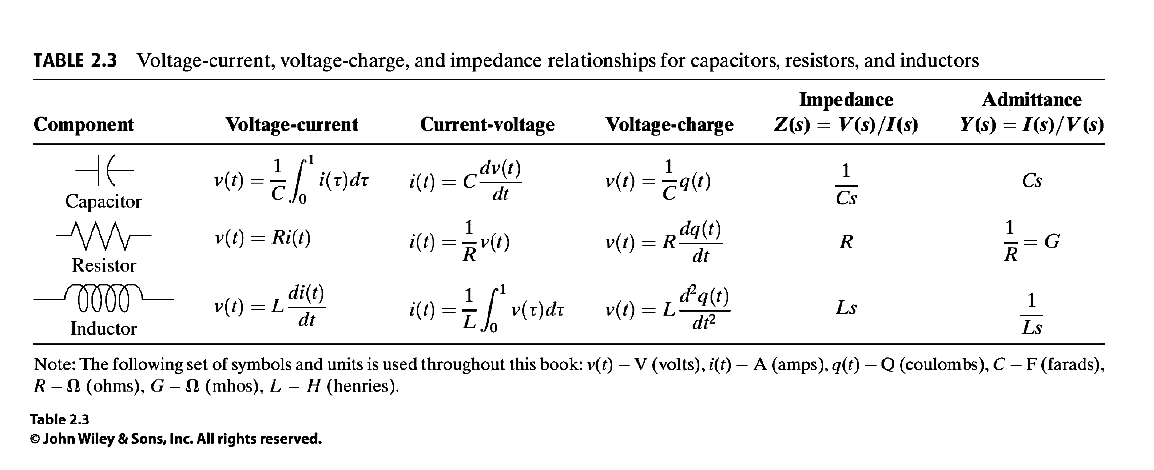Block One - A


  • Modelling in the frequency domain


    Transfer functions for general engineering systems *
    Linearisation



  • 2
    Voiceover

    4
    Voiceover



    Figure 2: Unit ramp

    6
    Voiceover



    Figure 4: Sine wave

    8
    Voiceover



    Figure 6: Exponential decay

    10
    Voiceover

    Time shift theorem

    \begin{align*} \mathcal{L}[f(t - T)] &\rightarrow e^{-s T} F(s) \\ \end{align*} So \begin{align*} g(t) &= f(t - T) &\implies&& G(s) = e^{-s T} F(s) \end{align*}

    A pure time delay (transport delay) of $T$ seconds can be introduced by multiplying the Laplace transform by $e^{-s T}$.
    Continues on next tab >
    1
    Voiceover

    Chapter 2 - The Laplace transform

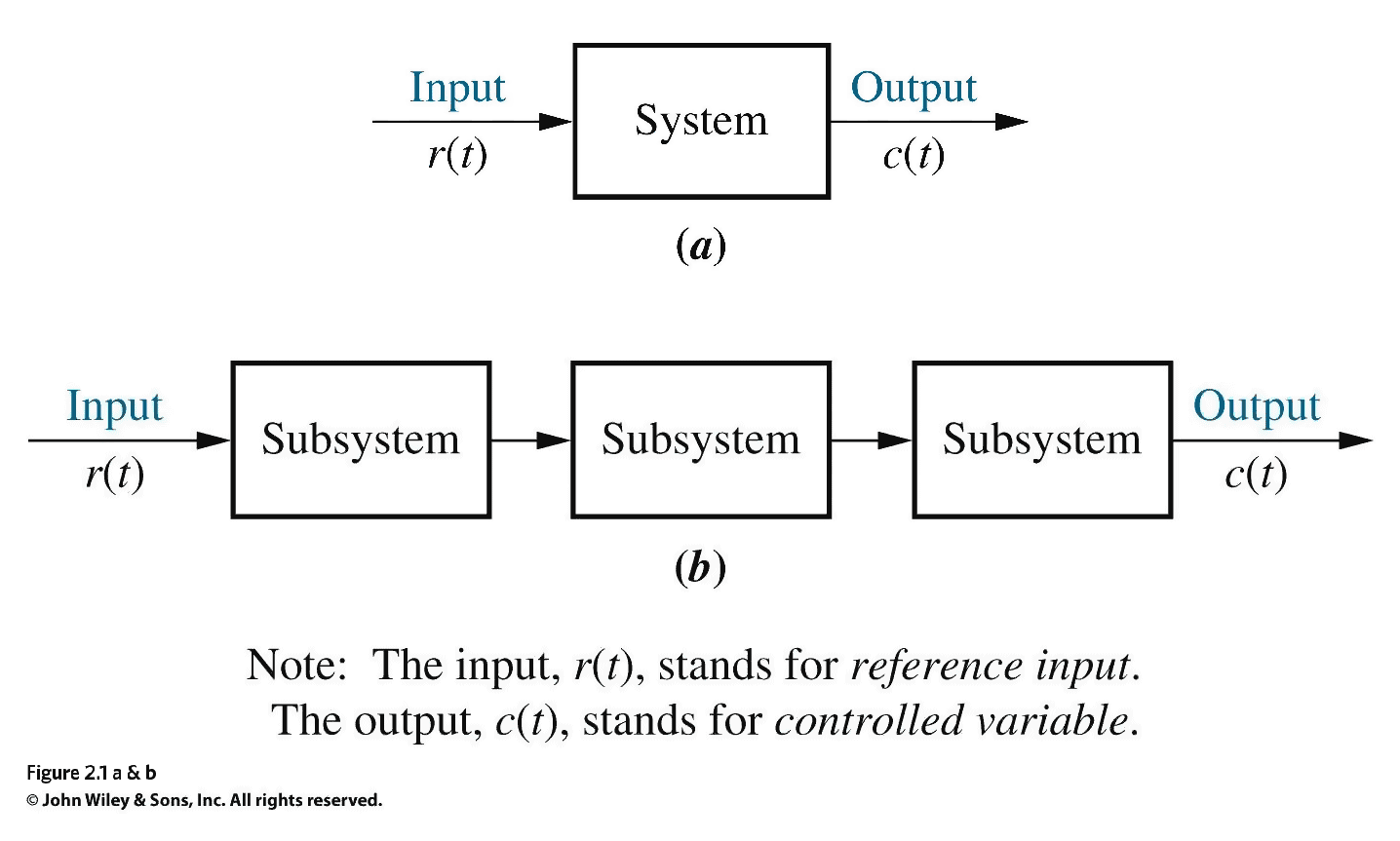
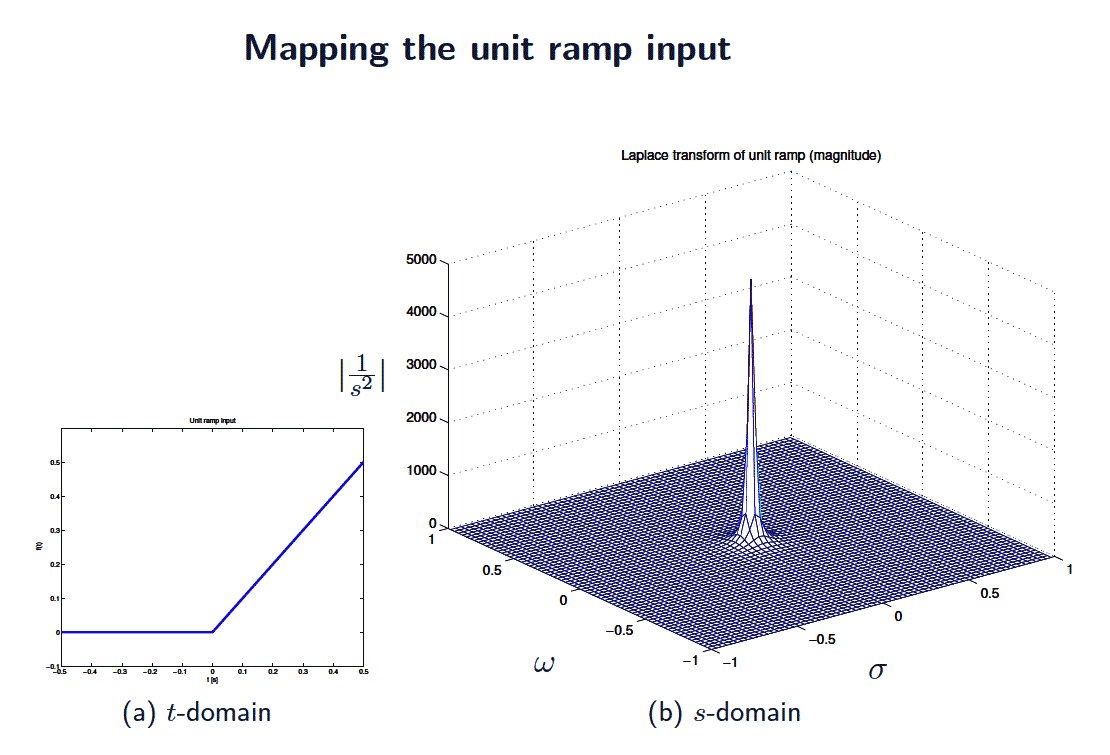
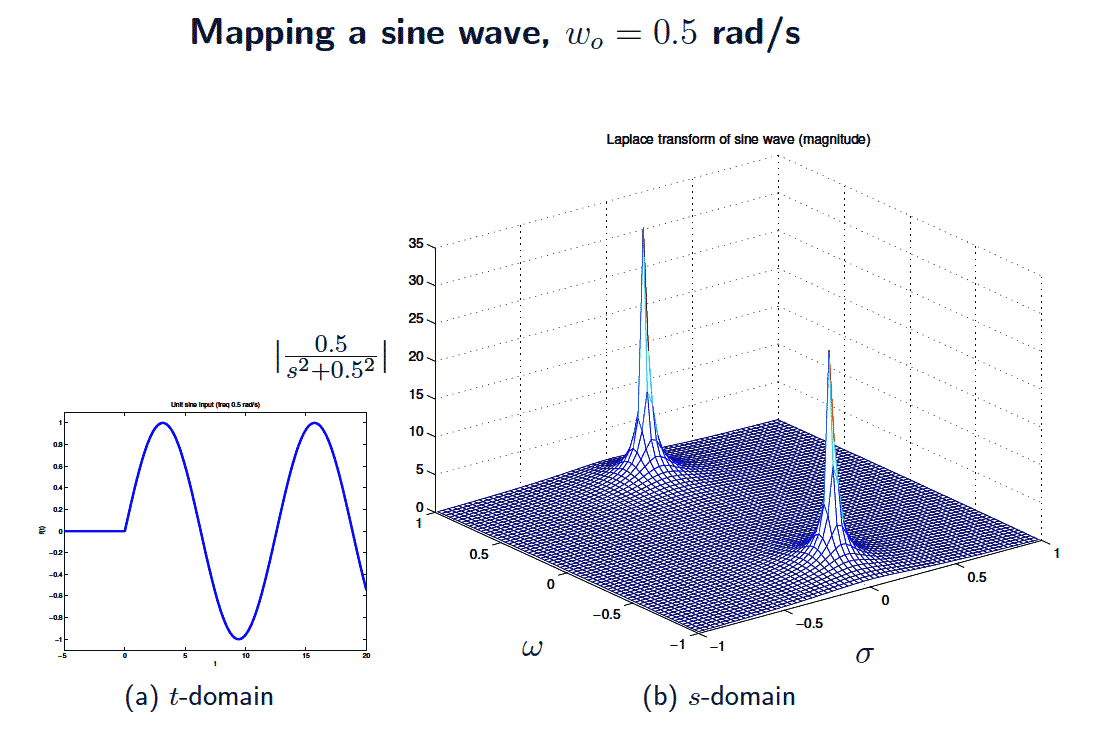
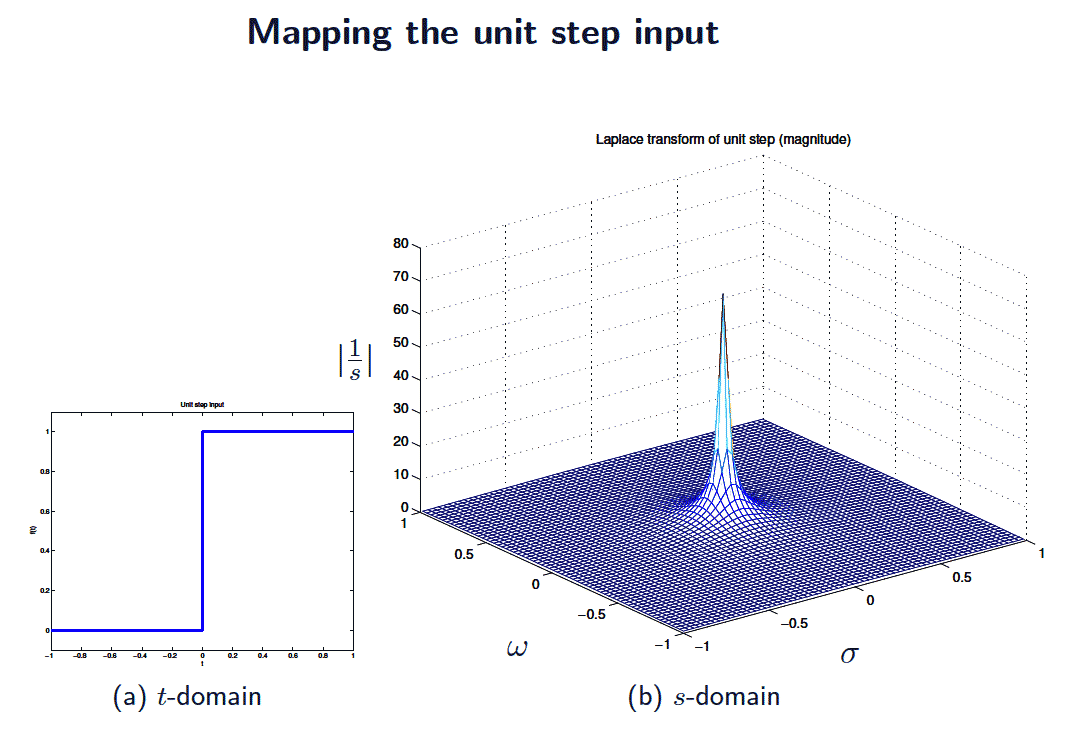
    The Laplace transform maps the whole of the time ($t$) domain to the complex $s$-plane \begin{align*} F(s) &= \displaystyle \mathcal{L}[f(t)] &=& \int_0^{\infty} f(t) e^{-st}\,\mathrm{d}t \\ &&&\\\end{align*} and its inverse maps $s$ back to $t$ \begin{align*}f(t) &= \displaystyle \mathcal{L}^{-1}[F(s)] &=& \frac{1}{2\pi j} \int_{\sigma - j \infty}^{\sigma + j \infty} F(s) e^{s t} \mathrm{d}s \end{align*}
    3
    Voiceover



    Figure 1: Unit step

    5
    Voiceover



    Figure 3: Standard input functions

    7
    Voiceover



    Figure 5: Exponential decay

    9
    Voiceover

    Linearity theorem

    \begin{align*} \mathcal{L}[k f(t)] &\rightarrow k F(s) \\ &\\ \mathcal{L}[f_1(t) + f_2(t)] &\rightarrow F_1(s) + F_2(s) \\ \end{align*} So \begin{align*} g(t) &= k f(t) &\implies&& G(s) = k F(s) \\ &&&&\\ g(t) &= f(t) + h(t) &\implies&& G(s) = F(s) + H(s) \end{align*}

  • 12
    Voiceover

    Scaling theorem

    \begin{align*} \mathcal{L}[f(at)] &\rightarrow \frac{1}{a} F\left(\frac{s}{a}\right) \\ \end{align*} So \begin{align*} g(t) &= f(at) &\implies&& G(s) = \frac{1}{a} F\left(\frac{s}{a}\right) \end{align*}
    14
    Voiceover

    Integration theorem

    \begin{align*} \mathcal{L}\left[ \int_0^t f(\tau) \mathrm{d}\tau \right] &= \frac{F(s)}{s} \end{align*}

    Integration is performed simply by dividing the Laplace transform by $s$.

    16
    Voiceover

    Initial value theorem

    \begin{align*} f(0_+) &= \lim_{s \rightarrow \infty} s F(s) \end{align*}
    18
    Voiceover

    MATLAB
    Laplace transform of $f(t) = e^{-a t}$ using MATLAB$^1$

    syms a t
    f = exp(-a*t)
    laplace(f)

    Inverse Laplace transform of $F(s) = \displaystyle \frac{1}{s+a}$ using MATLAB$^2$

    syms a s
    F = 1/(s+a)
    ilaplace(F)

    MATLAB1   MATLAB2

    20
    Voiceover

    Procedure

    1. Express $V_c(s)$ as a product of $G(s)$ and $V_0(s)$.

    2. Re-write $V_c(s)$ as a sum of simple terms using partial fractions.

    3. Manipulate terms algebraically to match entries in a table of Laplace transforms.

    4. Obtain inverse Laplace transform of each term using the table.

    5. Sum the inverse Laplace transforms.

    6. Verify answer.



    Continues on next tab >
    11
    Voiceover

    Frequency shift theorem

    \begin{align*} \mathcal{L}[e^{-a t} f(t)] &\rightarrow F(s+a) \\ \end{align*} So \begin{align*} g(t) &= e^{-a t} f(t) &\implies&& G(s) = F(s+a) \end{align*}
    13
    Voiceover

    Differentiation theorem

    \begin{align*} \mathcal{L}\left[ \frac{\mathrm{d}f(t)}{\mathrm{d}t} \right] &= s F(s) - f(0) \\ \mathcal{L}\left[ \frac{\mathrm{d}^2f(t)}{\mathrm{d}t^2} \right] &= s^2 F(s) - s f(0) - \frac{\mathrm{d}f}{\mathrm{d}t}(0) \\ \mathcal{L}\left[ \frac{\mathrm{d}^3f(t)}{\mathrm{d}t^3} \right] &= s^3 F(s) - s^2 f(0) - s \frac{\mathrm{d}f}{\mathrm{d}t}(0) - \frac{\mathrm{d}^2f}{\mathrm{d}t^2}(0) \\ \end{align*}

    If the initial conditions are zero, differentiation is performed simply by multiplying the Laplace transform by $s$.

    15
    Voiceover

    Final value theorem

    \begin{align*} f(\infty) &= \lim_{s \rightarrow 0} s F(s) \end{align*}

    For a unit step input, the final value can be found directly from the transfer function by letting $s \rightarrow 0$

    17
    Voiceover

    Key points, to all of the above

    If the initial conditions are zero, differentiation is performed simply by multiplying the Laplace transform by $s$.

    Integration is performed simply by dividing the Laplace transform by $s$.

    A pure time delay (transport delay) of $T$ seconds can be introduced by multiplying the Laplace transform by $e^{-s T}$.

    For a unit step input, the final value can be found directly from the transfer function by letting $s \rightarrow 0$

    19
    Voiceover

    Hand calculations

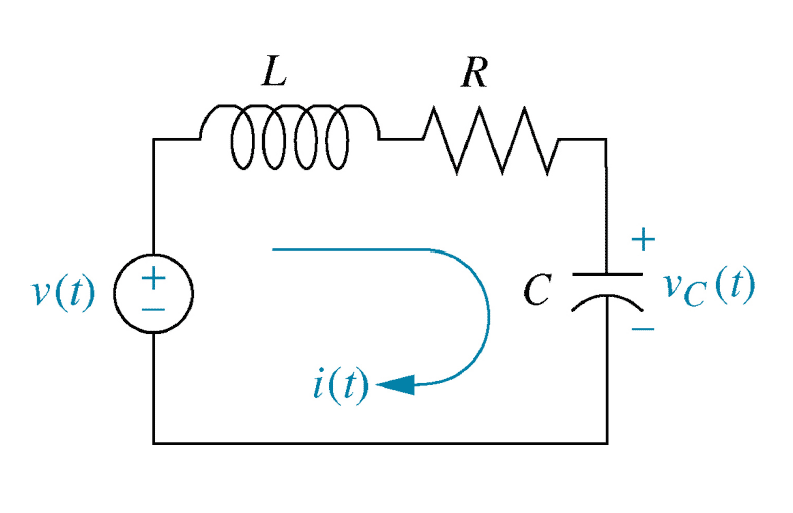
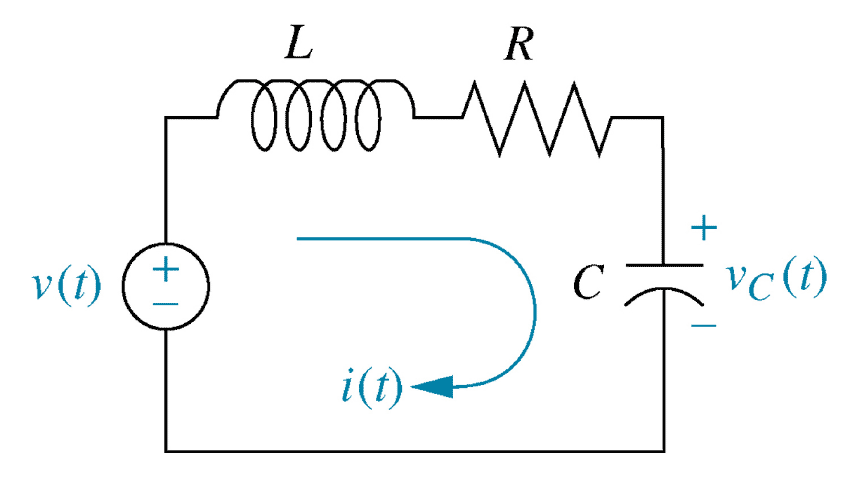
    Example: Second order LRC circuit
    An electrical LRC circuit is modelled by transfer function $G(s)$.
    \begin{align*} G(s) &= \frac{V_c}{V_{0}}(s) = \frac{1}{L C s^2 + R C s + 1} \end{align*} \begin{align} V_0 && \text{applied EMF} && (\text{volts,} \quad V)\\ V_c && \text{potential difference across capacitor} && (\text{volts,} \quad V)\\ L && \text{inductance} && (\text{henries,} \quad H)\\ R && \text{resistance} && (\text{ohms,} \quad \Omega)\\ C && \text{capacitance} && (\text{farads,} \quad F) \end{align}
    For given $L$, $R$ and $C$, find the potential difference across the capacitor $V_c(t)$ in response to a unit step input $V_0(t)$. \begin{align*} V_0(t) &= \begin{cases} 0 {\rm V} & \text{if } t \leq 0 \\ 1 {\rm V} & \text{if } t \gt 0 \end{cases} & V_0(s) &= \frac{1}{s} \end{align*}
  • 22
    Voiceover

    Partial fraction expansion

    Factorise $G(s)$, using $s = \frac{-b\pm\sqrt{b^2-4ac}}{2a}$ if necessary, to find the denominators. \begin{align*} s &= \frac{-12\pm\sqrt{12^2-4\times 20}}{2\times 1} & s=-2 \text{or }s=-10 \end{align*} $\qquad \qquad \qquad \text{Hence} $ \begin{align*} V_c(s) &=\frac{20}{s^2 + 12 s + 20} \times \frac{1}{s} \\ &= \frac{20}{s(s+2)(s+10)} \\ &= \frac{A}{s} + \frac{B}{s+2} + \frac{C}{s+10} \end{align*}
    Next: all unique linear factors, so find $A, B,$ and $C$ using Heaviside's Quick Cover-Up method.


    24
    Voiceover

    Inverse Laplace transform

    Standard transform table has entries for $\displaystyle \frac{1}{s}$ and $\displaystyle \frac{1}{s+a}$ or $\displaystyle \frac{a}{s+a}$. \begin{align*} V_c(s) &=& \frac{1}{s} && -\frac{1.25}{s+2} && +\frac{0.25}{s+10} \\ \\ &=& \frac{1}{s} && -1.25 \times \frac{1}{s+2} && +0.25 \times \frac{1}{s+10} \\ \\ V_c(t) &=& \mathcal{L^-{^1}}{\Bigg[\frac{1}{s}\Bigg]} &&- 1.25 \times \mathcal{L^-{^1}}{\Bigg[\frac{1}{s+2}\Bigg]} &&+ 0.25 \times \mathcal{L^-{^1}}{\Bigg[\frac{1}{s+10}\Bigg]} \end{align*} Next: look up the inverse Laplace transforms.

    26
    Voiceover

    Output
    \begin{align*} \large V_c(t) &= \large 1 - 1.25 e^{-2 t} + 0.25 e^{-10 t} \end{align*}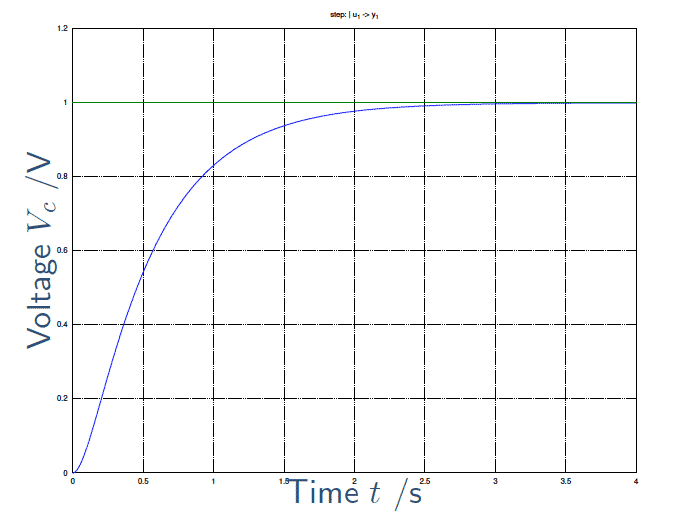
    Figure 7

    28
    Voiceover

    Critically-damped: $G(s)$ has repeated real root: $(RC)^2=4LC $


    Example: $L=1$ H, $R=20 \Omega$, $C=0.01$ F. % s=-10
    \begin{align*} G(s) &= \frac{V_c}{V_{0}}(s) = \frac{1}{L C s^2 + R C s + 1} & V_0(s) &= \frac{1}{s} \end{align*} \begin{align*} V_c(s) &= G(s) \times V_0(s) \\ &= \frac{1}{0.01 s^2 + 0.2 s + 1} \times \frac{1}{s} = \frac{100}{s^2 + 20 s + 100} \times \frac{1}{s} \end{align*}
    Next: re-write $V_c$ as a sum of terms using partial fractions.


    30
    Voiceover

    Partial fraction coefficients
    \begin{align*} V_c(s) &= \frac{100}{s(s+10)(s+10)} = \frac{A}{s} + \frac{B}{s+10} + \frac{C}{(s+10)^2} \end{align*} Cross-multiplying and equating coefficients of $s^n$ \begin{align*} 100 &= A(s+10)^2 + Bs(s+10) + Cs \\ &= (A+B)s^2 + (20A+10B+C)s + 100A \end{align*} \begin{align*} s^2: && 0 &= A+B &&\implies B = -A\\ s^1: && 0 &= 20A+10B+C &&\implies C = -10A\\ s^0: && 100 &= 100 A && \implies A = 1 \end{align*}
    $\qquad \qquad \qquad \text{Hence} $
    \begin{align*} A &= 1 & B &= -1 & C &= -10 \end{align*}
    Continues on next tab >
    21
    Voiceover

    Over-damped: $G(s)$ has 2 real roots: $(RC)^2 \gt 4LC$


    Example: $L=0.5$ H, $R=6 \Omega$, $C=0.1$ F. % s=-2,-10
    \begin{align*} G(s) &= \frac{V_c}{V_{0}}(s) = \frac{1}{L C s^2 + R C s + 1} & V_0(s) &= \frac{1}{s} \end{align*} \begin{align*} V_c(s) &= G(s) \times V_0(s) \\ &= \frac{1}{0.05 s^2 + 0.6 s + 1} \times \frac{1}{s} = \frac{20}{s^2 + 12 s + 20} \times \frac{1}{s} \end{align*}
    Next: re-write $V_c$ as a sum of terms using partial fractions.


    23
    Voiceover

    Partial fraction coefficients

    \begin{align*} V_c(s) =\frac{20}{s(s+2)(s+10)} = \frac{A}{s} + \frac{B}{s+2} + \frac{C}{s+10} \end{align*} Using Heaviside's Quick Cover-Up method \begin{align*} A &= 1 \quad & B &= -\frac{5}{4} = -1.25 \quad & C &= \frac{1}{4} = 0.25 \end{align*} \begin{align*} V_c(s) &= \frac{1}{s} - \frac{1.25}{s+2} + \frac{0.25}{s+10} \end{align*}
    Next: manipulate terms to match entries in table of transforms.

    25
    Voiceover

    Inverse Laplace transform

    \begin{align*} \mathcal{L^-{^1}}{\Bigg[\frac{1}{s}}\Bigg] &= 1 & \mathcal{L^-{^1}}{\Bigg[\frac{1}{s+a}}\Bigg] &= e^{-at} \end{align*} \begin{align*} V_c(t) &= \mathcal{L^-{^1}}{\Bigg[\frac{1}{s}\Bigg]} &-& 1.25 \times \mathcal{L^-{^1}}{\Bigg[\frac{1}{s+2}\Bigg]} &+& 0.25 \times \mathcal{L^-{^1}}{\Bigg[\frac{1}{s+10}\Bigg]} \\ \\ &= 1 &-& 1.25 \times e^{-2t} &+& 0.25 \times e^{-10t} \end{align*}
    Finally, verify! (How?)

    27
    Voiceover

    Verification with MATLAB
    L = 0.5; R = 6; C = 0.1;
    % visual check
    G = tf( 1, [ L*C, R*C, 1 ]);
    [y, t] = step(G);
    x = 1 - 1.25.*exp(-2*t) + 0.25.*exp(-10*t);
    figure(1): plot(t,y); title('Step response');
    figure(2); plot(t,x); title('Hand calc');
    figure(3); plot(t,y-x); title('Difference')

    % symbolic check
    syms s
    ilaplace(1/(L*C*s^2+R*C*s+1)*(1/s))
    29
    Voiceover

    Partial fraction expansion
    Factorise $G(s)$, using $s = \frac{-b\pm\sqrt{b^2-4ac}}{2a}$ if necessary, to find the denominators. \begin{align*} s &= -10 \text{(repeated)} \end{align*} \begin{align*} V_c(s) &= \frac{100}{s^2 + 20 s + 100} \times \frac{1}{s} \\ &= \frac{100}{s(s+10)(s+10)} \\ &= \frac{A}{s} + \frac{B}{s+10} + \frac{C}{(s+10)^2} \end{align*}
    Next: repeated factors, so cross-multiply and equate coefficients.


  • 32
    Voiceover

    Output
    \begin{align*} \large V_c(t) &= \large 1 - e^{-10 t} - 10 t e^{-10 t} \end{align*}

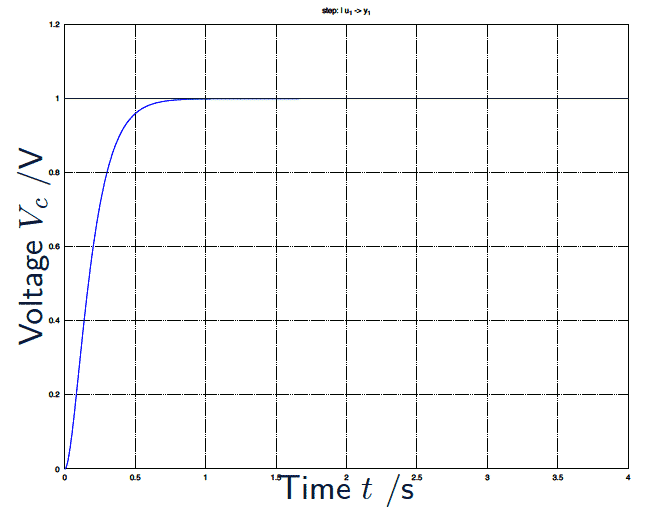
    Figure 8

    34
    Voiceover

    Partial fraction expansion

    Factorising the quadratic would yield complex roots, so it is better to keep that whole. \begin{align*} V_c(s) &= \frac{10}{s^2+6 s + 10} \times \frac{1}{s} = \frac{A s + B}{s^2 + 6 s + 10} + \frac{C}{s} \end{align*} Cross-multiplying and equating coefficients of $s^n$ \begin{align*} 10 &= (As + B)s + C(s^2+6s+10) \\ &= (A+C) s^2 + (B+6C) s + 10 C \end{align*} \begin{align*} s^2: && 0 &= A+C &&\implies A = -C\\ s^1: && 0 &= B+6C &&\implies B = -6C\\ s^0: && 10 &= 10 C && \implies C = 1 \end{align*} \begin{align*} \therefore A &= -1 & B &= -6 & C &= 1 \end{align*}
    36
    Voiceover

    Completing the square
    \begin{align*} V_c(s) &= \frac{1}{s} - \frac{s+6}{s^2+6s+10} \\ \end{align*}
    \begin{align*} s^2+6s+10 &= \left(s+\frac{6}{2}\right)^2 + \omega^2 \\ &= s^2 + 6s + 9 + \omega^2 &\implies \omega^2 = 1 \\ &= (s+3)^2 + \sqrt{1}^2 \end{align*}
    \begin{align*} V_c(s) &= \frac{1}{s} - \frac{s+6}{(s+3)^2+1^2} = \frac{1}{s} - \frac{s+3}{(s+3)^2+1^2} - \frac{3}{(s+3)^2+1^2} \end{align*} Next: inverse transforms.
    38
    Voiceover

    Output
    \begin{align*} \large V_c(t) &= \large 1 - e^{-3 t} \cos t + 3 \sin t & \;\;\;\large (\zeta = 0.95) \end{align*}

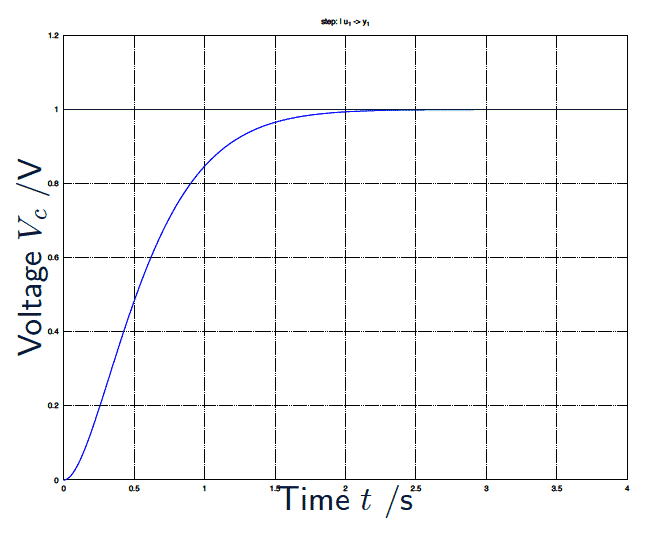
    Figure 9
    40
    Voiceover

    Parameters

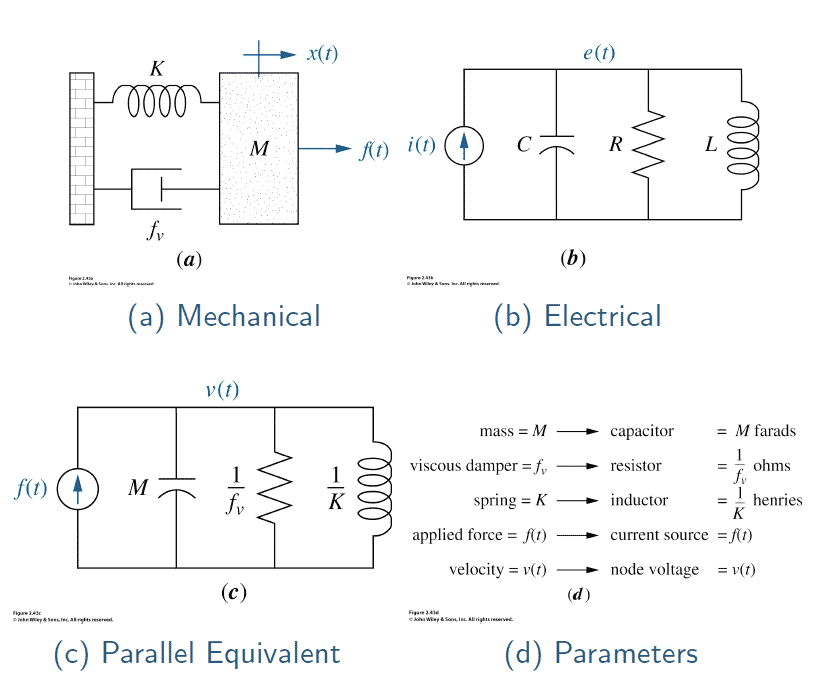
    Over-damped, $G(S)$ has 2 real roots: $f_v^2 \gt 4mK$
    Example: $m=1$ kg, $f_v=3$ N$\cdot$s/m, $K=2$ N/m. % s=-1,-2

    Critically-damped, $G(s)$ has repeated real root: $f_v^2=4mK$
    Example: $m=1$ kg, $f_v=2$ N$\cdot$s/m, $K=1$ N/m. % s=-1

    Under-damped, $G(s)$ has complex pair of roots: $f_v^2 \lt 4mK$
    Example: $m=1$ kg, $f_v=2$ N$\cdot$s/m, $K=2$ N/m. % s=-1+/-j

    Solve by hand and verify in Matlab. Numbers differ, but the method for each case is identical to the electrical examples.
    31
    Voiceover

    Inverse Laplace transform
    Standard transforms
    \begin{align*} \mathcal{L^-{^1}}{\Bigg[\frac{1}{s}\Bigg]} &= 1 & \mathcal{L^-{^1}}{\Bigg[\frac{1}{s+a}\Bigg]} &= e^{-at} & \mathcal{L^-{^1}}{\Bigg[\frac{1}{(s+a)^2}\Bigg]} &= t \times e^{-at} \end{align*} \begin{align*} V_c(s) &= \frac{1}{s} &&- \frac{1}{s+10} &&- \frac{10}{(s+10)^2} \\ \\ &= \frac{1}{s} &&- \frac{1}{s+10} &&- 10 \times \frac{1}{(s+10)^2} \\ V_c(t) &= \mathcal{L^-{^1}}{\Bigg[\frac{1}{s}\Bigg]} &&- \mathcal{L^-{^1}}{\Bigg[\frac{1}{s+10}\Bigg]} &&- 10 \times \mathcal{L^-{^1}}{\Bigg[\frac{1}{(s+10)^2}\Bigg]} \\ \\ &= 1 &&- e^{-10t} &&-10 \times t \times e^{-10t} \end{align*}
    33
    Voiceover

    Chapter 2 - The Laplace transform

    Under-damped, $G(s)$ has complex pair of roots: $(RC)^2 \lt 4LC$

    Example: $L=1$ H, $R=6 \Omega$, $C=0.1$ F. % s=-3+/-j
    \begin{align*} G(s) &= \frac{V_c}{V_{0}}(s) = \frac{1}{L C s^2 + R C s + 1} & V_0(s) &= \frac{1}{s} \end{align*}
    \begin{align*} V_c(s) &= G(s) \times V_0(s) \\ &= \frac{1}{0.1 s^2 + 0.6 s + 1} \times \frac{1}{s} = \frac{10}{s^2 + 6 s + 10} \times \frac{1}{s} \end{align*}
    Next: re-write $V_c$ as a sum of terms using partial fractions.
    35
    Voiceover

    Completing the square

    Recall the standard inverse transforms. \begin{align*} \mathcal{L^-{^1}}{\Bigg[\frac{s}{s^2+\omega^2}\Bigg]} &= \cos \omega t & \mathcal{L^-{^1}}{\Bigg[\frac{1}{s}\Bigg]} &= 1 \\ \mathcal{L^-{^1}}{\Bigg[\frac{\omega}{s^2+\omega^2}\Bigg]} &= \sin \omega t & \mathcal{L^-{^1} [\mathit{F}(s+a)]} &= e^{-at} \mathcal{L^-{^1}{ [\mathit{F}(s)]}} \end{align*} \begin{align*} V_c(s) &= \frac{1}{s} - \frac{s+6}{s^2+6s+10} \end{align*} The inverse transform of the quadratic term can be found by ''completing the square'' and using the frequency shift theorem.

    Next: completing the square
    37
    Voiceover

    Inverse Laplace transform
    Again recall the standard inverse transforms. \begin{align*} \mathcal{L^-{^1}}{\Bigg[\frac{s}{s^2+\omega^2}\Bigg]} &= \cos \omega t & \mathcal{L^-{^1}}{\Bigg[\frac{1}{s}\Bigg]} &= 1 \\ \mathcal{L^-{^1}}{\Bigg[\frac{\omega}{s^2+\omega^2}\Bigg]} &= \sin \omega t & \mathcal{L^-{^1}}{[F(s+a)]} &= e^{-at} \mathcal{L^-{^1}}{[F(s)]} \end{align*}
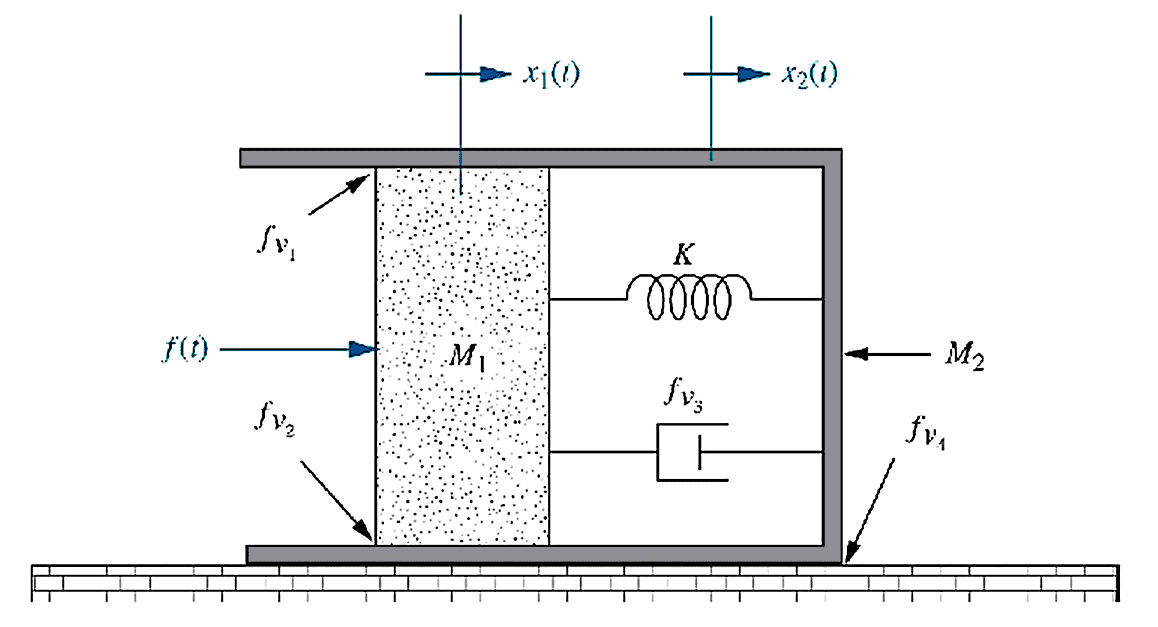
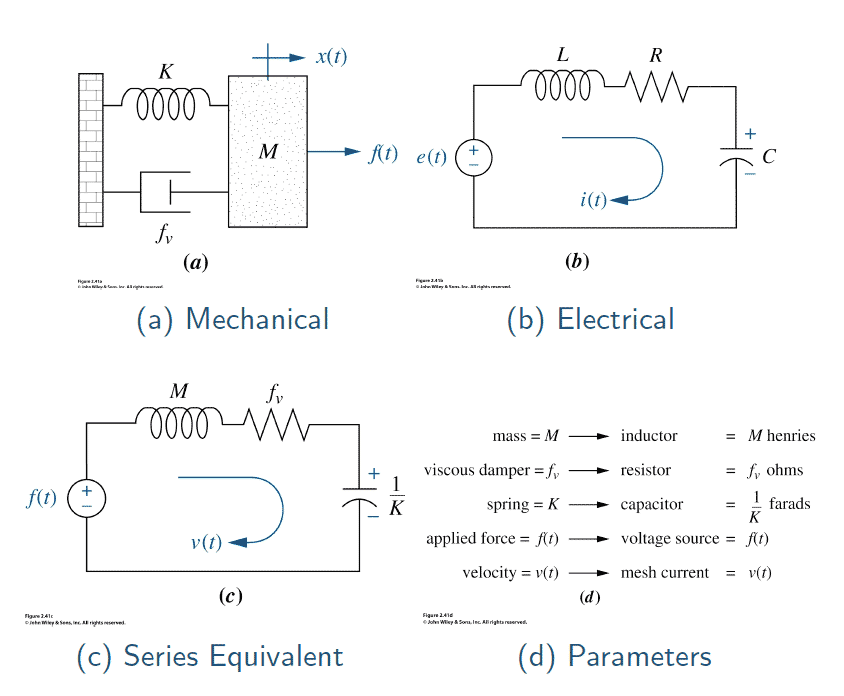
    \begin{align*} V_c(s) &=& \frac{1}{s} &- \frac{s+3}{(s+3)^2+1^2} &- 3\times \frac{1}{(s+3)^2+1^2} \\ \\ V_c(t) &=& \mathcal{L^-{^1}}{\Bigg[\frac{1}{s}\Bigg]} &- \mathcal{L^-{^1}}{\Bigg[\frac{s+3}{(s+3)^2+1^2}\Bigg]} &- 3\times\mathcal{L^-{^1}}{\Bigg[\frac{1}{(s+3)^2+1^2}\Bigg]} \\ \\ &=& 1 &- e^{-3t} \cos t &- 3 \times e^{-3t} \sin t \end{align*}
    39
    Voiceover

    Example: Second order mechanical system A mechanical mass-damper-spring system is modelled by the transfer function $G(s)$. \begin{align*} G(s) &= \frac{X}{F}(s) = \frac{1}{ms^2 + f_v s + K} \end{align*} $$ \begin{array}{abcde} F & \text{applied force} & \text{(newtons,} & \text{N)} \\ X & \text{displacement} & \text{((metres,} & \text{m)}\\ m & \text{mass} & \text{((kilogrammes,} & \text{kg)}\\ f_v & \text{damping} & \text{((newton-seconds per metre,} & \text{N·s/m))}\\ K & \text{spring stiffness} & \text{((newtons per metre,} & \text{N/m))}\\ \end{array} $$
    For given $m$, $f_v$, $K$, find the displacement $X(t)$ in response to a unit step input $F(t)$. \begin{align*} F(t) &= \begin{cases} 0 {\rm N} & \text{if } t \leq 0 \\ 1 {\rm N} & \text{if } t \gt 0 \end{cases} & F(s) &= \frac{1}{s} \end{align*}









  • 42
    Voiceover

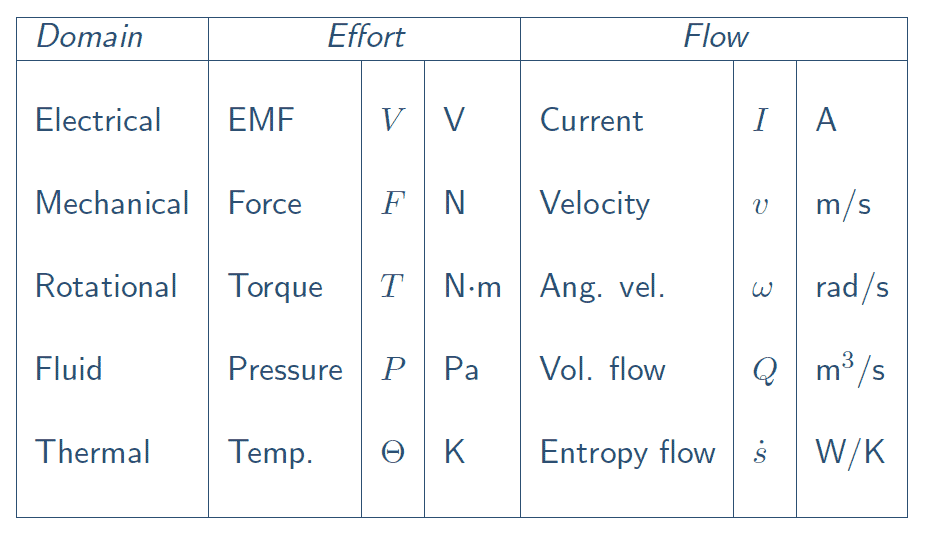
    Physical systems

    Physical systems are governed by conservation laws:
    Conservation of Energy (including Mass)
    Conservation of Momentum
    Conservation of Angular Momentum
    Conservation of Electric Charge

    44
    Voiceover

    Co-variables with power as the product


    Figure 10
    46
    Voiceover

    Ideal Electrical Components

    LRC circuit

    Figure 11: LRC circuit
    48
    Voiceover

    Ideal Mechanical Components (Translational)

    Mass Spring Damper



    Figure 12
    41
    Voiceover

    Chapter 2 - Modelling

    Mathematical modelling

    1. Determine the equations that govern the individual components
    Hooke's Law (springs)
    Ohm's Law (resistance)
    Faraday's Law (induction)

    2. Determine how the components interact
    Newton's Laws (motion)
    Kirchhoff's Circuit Laws (KCL, KVL)

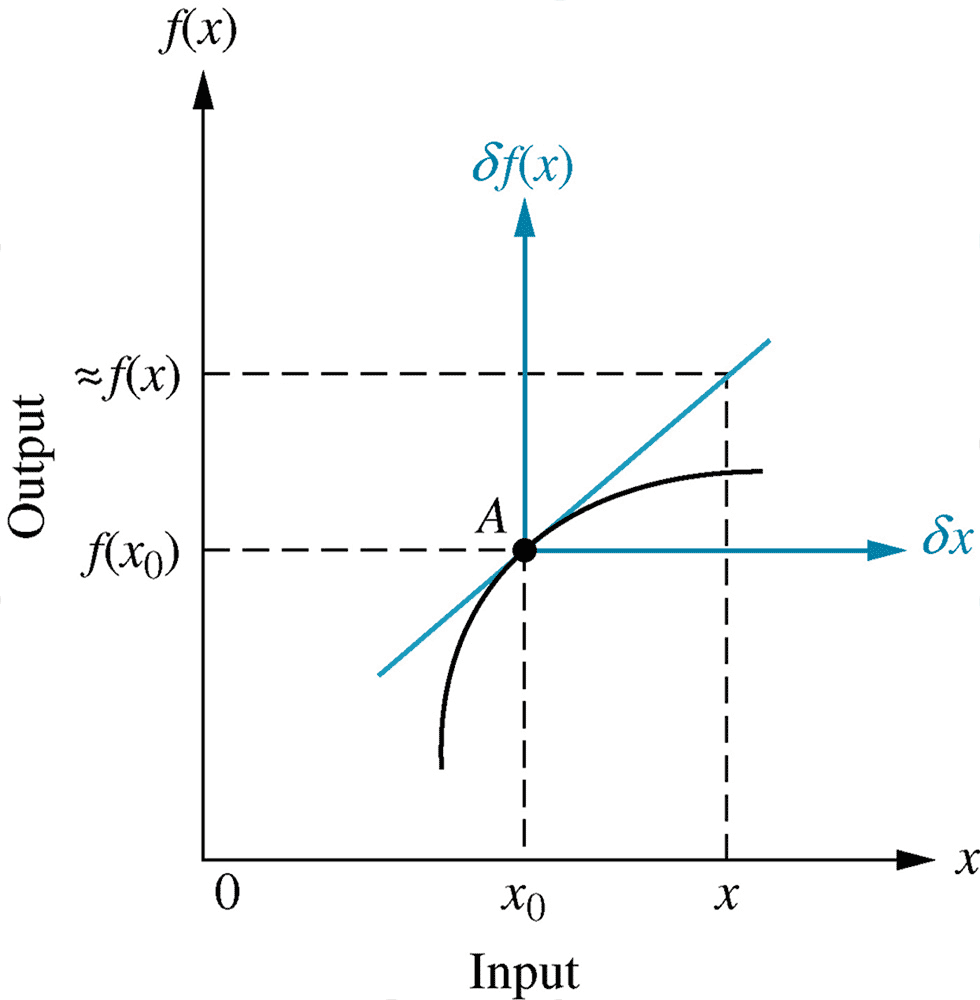
    3. Make approximations and simplifications
    Linearisation
    Thévenin's and Mayer-Norton's
    43
    Voiceover

    Energetic systems

    Power is the universal currency of physical systems.

    Intra-domain interaction:
    Electrical-Electrical
    Mechanical-Mechanical

    Inter-domain interaction:
    Electrical-Mechanical (Mechatronics)
    Thermal-Fluid (Thermofluids)

    Power must be conserved at all times in each interaction.
    45
    Voiceover

    Components

    Components

    Ideal Electrical
    Ideal Mechanical
    Ideal Rotational
    Ideal Transformers

    47
    Voiceover

    Constitutive Relations: Electrical


    Ideal Inductor
    \begin{align*} \large I &= \frac{\lambda}{L} & \qquad \frac{\mathrm{d} \lambda}{\mathrm{d}t} &= V \end{align*}

    Ideal Resistor
    \begin{align*} \large V &= I R \end{align*}

    Ideal Capacitor
    \begin{align*} \large V &= \frac{q}{C} & \qquad \large \frac{\mathrm{d}q}{\mathrm{d}t} &= I \end{align*}
    49
    Voiceover

    Constitutive Relations: Mechanical


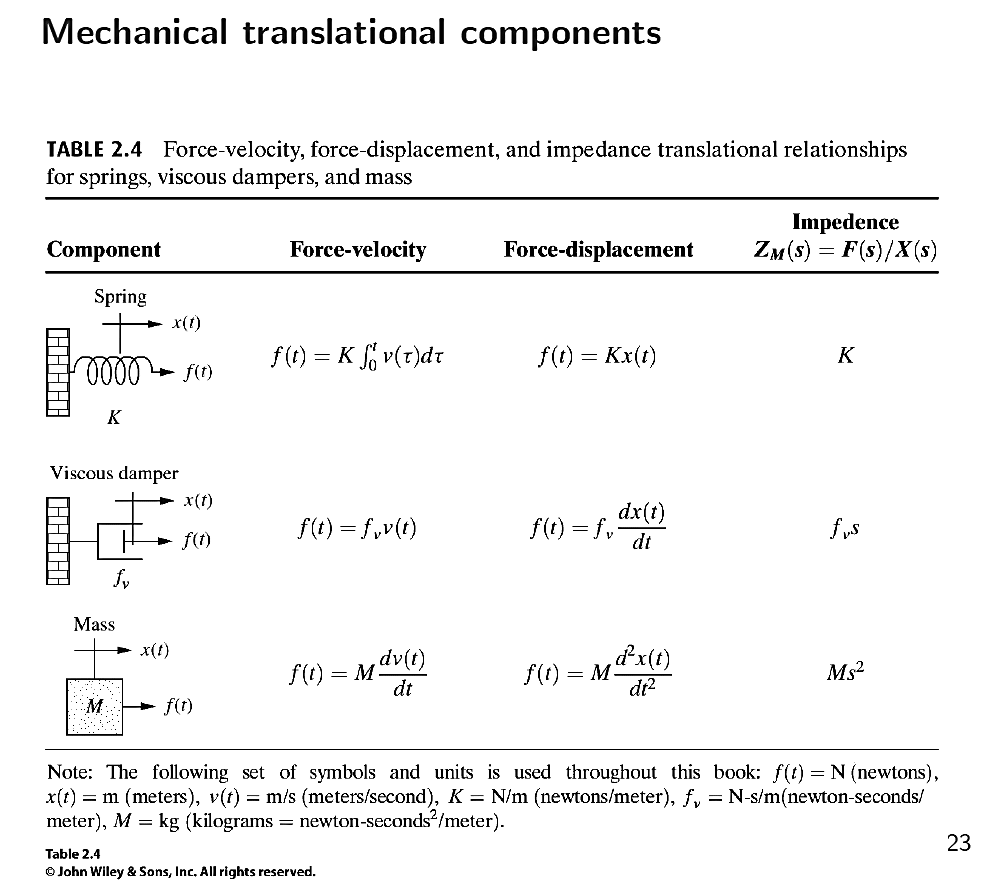
    Ideal Mass
    \begin{align*} \large v &= \frac{p}{m} & \qquad \frac{\mathrm{d}p}{\mathrm{d}t} &= F \end{align*}

    Ideal Damper
    \begin{align*} \large F &= f_v v \end{align*}

    Ideal Spring
    \begin{align*} \large F &= K x & \qquad \frac{\mathrm{d}x}{\mathrm{d}t} &= v \end{align*}



  • 51
    Voiceover

    Constitutive Relations: Rotational


    Ideal Inertia
    \begin{align*} \large \omega &= \frac{p}{J} & \qquad\frac{\mathrm{d}p}{\mathrm{d}t} &= T \end{align*}

    Ideal Damper
    \begin{align*} \large T &= D \omega \end{align*}

    Ideal Spring
    \begin{align*} \large T &= K \theta & \qquad \frac{\mathrm{d}\theta}{\mathrm{d}t} &= \omega \end{align*}
    53
    Voiceover

    Levers


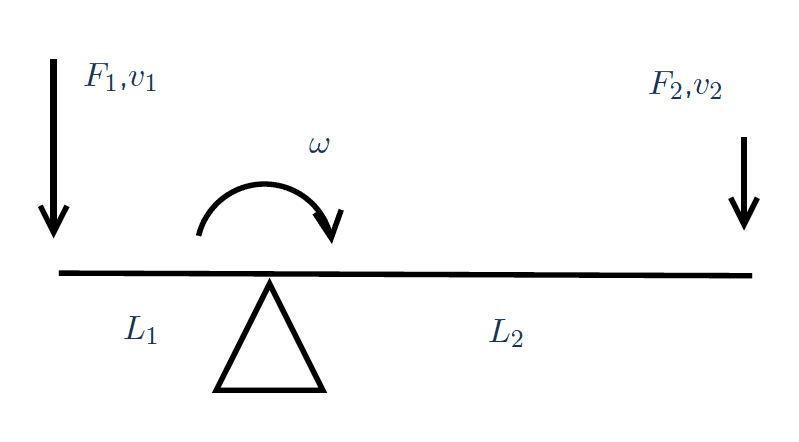
    Figure 14

    \begin{align*} \large\frac{v_1}{L_1} &= \large\omega = \frac{v_2}{L_2} \end{align*}
    \begin{align*} \large\frac{v_1}{v_2} &= \large\frac{L_1}{L_2} \end{align*}
    55
    Voiceover

    Constitutive Relations: Motors


    Ideal Motor
    \begin{align*} \large V_1 I_1 &= T_2 \omega_2 & \qquad \frac{T_2}{V_1} &= \large n = \frac{I_1}{\omega_2} \end{align*}

    Ideal Cam or Rack & Pinion, etc.
    \begin{align*} \large T_1 \omega_1 &= \large F_2 v_2 & \qquad \frac{F_2}{T_1} &= n = \frac{\omega_1}{v_2} \end{align*}

    57
    Voiceover

    Modelling (Cont.)

    Impedance and Admittance: Electrical


    Ideal Inductor
    \begin{align*} \large I &= \frac{\lambda}{L} & \qquad \frac{\mathrm{d}\lambda}{\mathrm{d}t} &= V \end{align*}

    Ideal Resistor
    \begin{align*} \large V &= I R \end{align*}

    Ideal Capacitor
    \begin{align*} \large V &= \frac{q}{C} & \qquad \frac{\mathrm{d}p}{\mathrm{d}t} &= I \end{align*}
    59
    Voiceover

    Impedance and Admittance: Electrical


    Ideal Inductor
    \begin{align*} \large \frac{V}{I} &= L s & \frac{I}{V} &= \frac{1}{L s} \end{align*}

    Ideal Resistor
    \begin{align*} \large \frac{V}{I} &= R & \frac{I}{V} &= \frac{1}{R} \end{align*}

    Ideal Capacitor
    \begin{align*} \large \frac{V}{I} &= \frac{1}{C s} & \frac{I}{V} &= C s \end{align*}

    (Nise, p 49 / 47)
    Continues on next tab
    50
    Voiceover

    Ideal Mechanical Components (Rotational)

    Mass Spring Damper



    Figure 13
    52
    Voiceover

    Ideal Transformer Components

    Constitutive Relations: Transformers

    Ideal Electrical Transformer
    \begin{align*} \large V_1 I_1 &= V_2 I_2 & \frac{V_2}{V_1} &= n = \frac{I_1}{I_2} & n = \frac{N_2}{N_1} \end{align*}

    Ideal Mechanical Lever
    \begin{align*} \large F_1 v_1 &= F_2 v_2 & \frac{F_2}{F_1} &= n = \frac{v_1}{v_2} & n = \frac{L_1}{L_2} \end{align*}

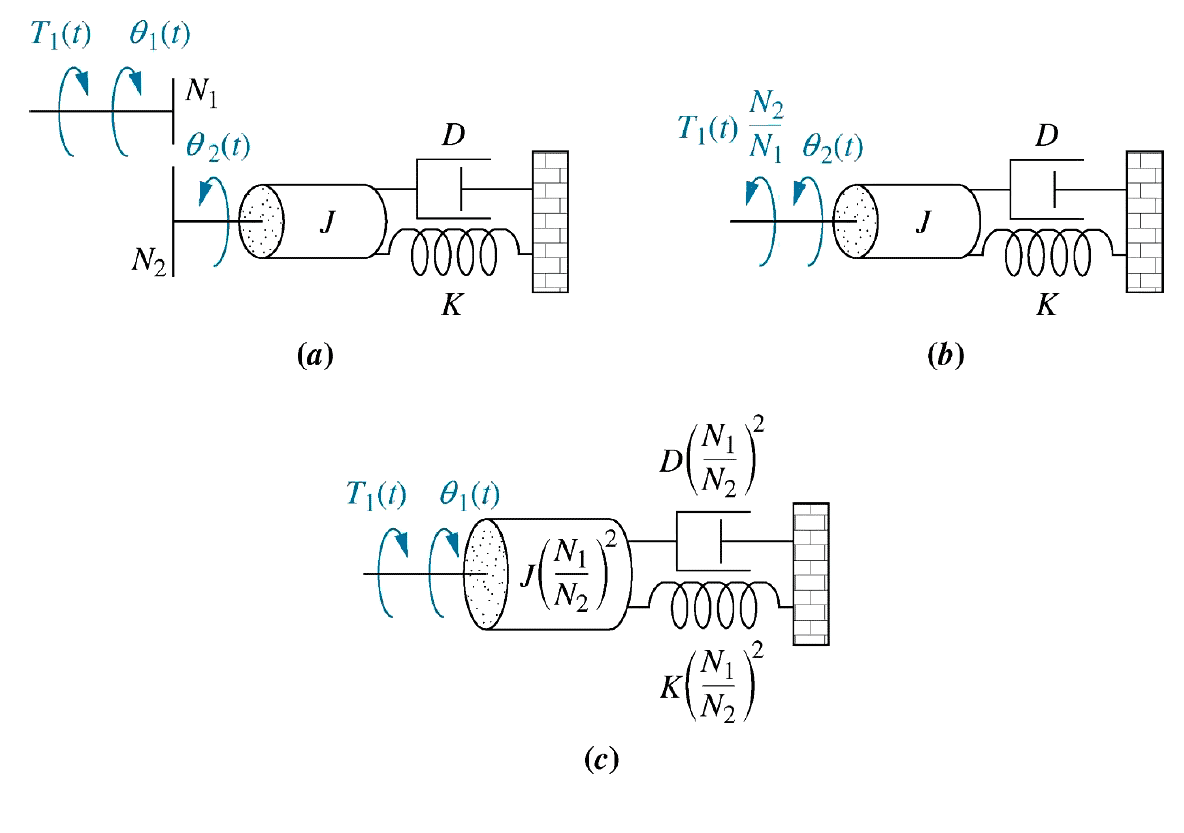
    Ideal Rotational Gear
    \begin{align*} \large T_1 \omega_1 &= T_2 \omega_2 & \frac{T_2}{T_1} &= n = \frac{\omega_1}{\omega_2} & n = \frac{D_2}{D_1} \end{align*}
    54
    Voiceover

    Gears


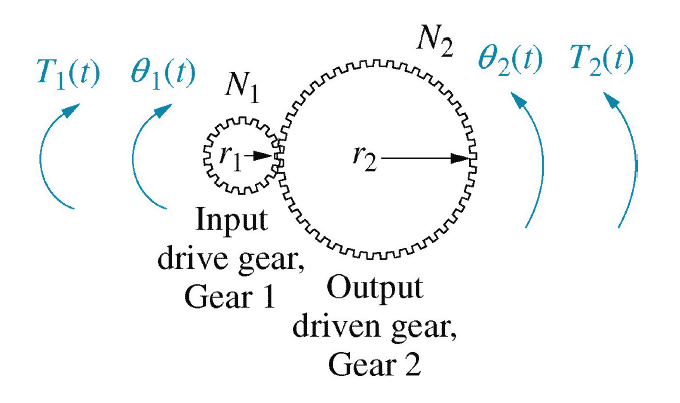
    Figure 15

    \begin{align*} \large r_1 \omega_1 &= \large v = r_2 \omega_2 \end{align*} \begin{align*} \large \frac{\omega_1}{\omega_2} &= \large \frac{r_2}{r_1} \end{align*}
    56
    Voiceover

    Impedance and Admittance


    Impedance
    \begin{align*} \large Z(s) &= \frac{V}{I}(s) & Z_M(s) &= \frac{F}{x}(s) & Z_M(s) &= \frac{T}{\theta}(s) \\ \end{align*}

    Admittance
    \begin{align*} \large Y(s) &=\frac{I}{V}(s) & Y_M(s) &= \frac{x}{F}(s) & Y_M(s) &= \frac{\theta}{T}(s) \\ \end{align*}

    58
    Voiceover

    Impedance and Admittance: Electrical


    Ideal Inductor
    \begin{align*} \large I &= \frac{\lambda}{L} & \qquad s \lambda &= V \end{align*}

    Ideal Resistor
    \begin{align*} \large V &= I R \end{align*}

    Ideal Capacitor
    \begin{align*} \large V &= \frac{q}{C} & \qquad s q &= I \end{align*}
  • 61
    Voiceover

    Impedance and Admittance: Mechanical


    Ideal Mass
    \begin{align*} \large v &= \frac{p}{m} & \qquad s p &= F \end{align*}

    Ideal Damper
    \begin{align*} \large F &= f_v v \end{align*}

    Ideal Spring
    \begin{align*} \large F &= K x & \qquad s x &= v \end{align*}
    63
    Voiceover

    Impedance and Admittance: Rotational


    Ideal Inertia
    \begin{align*} \large \omega &= \frac{p}{J} & \qquad \frac{\mathrm{d}p}{\mathrm{d}t} &= T \end{align*}

    Ideal Damper
    \begin{align*} \large T &= D \omega \end{align*}

    Ideal Spring
    \begin{align*} \large T &= K \theta & \qquad \frac{\mathrm{d}\theta}{\mathrm{d}t} &= \omega \end{align*}
    65
    Voiceover

    Impedance and Admittance: Rotational


    Ideal Inertia
    \begin{align*} \large \frac{T}{\omega} &= J s & \qquad \large \frac{\omega}{T} &= \frac{1}{J s} \end{align*}

    Ideal Damper
    \begin{align*} \large \frac{T}{\omega} &= D & \qquad \large \frac{\omega}{T} &= \frac{1}{D} \end{align*}

    Ideal Spring
    \begin{align*} \large \frac{T}{\omega} &= \frac{K}{s} & \qquad \large \frac{\omega}{T} &= \frac{s}{K} \end{align*}
    67
    Voiceover
    Impedance and Admittance: Translational


    Ideal Mass
    \begin{align*} \large \frac{F}{x} &= m s^2 & \qquad \large \frac{x}{F} &= \frac{1}{m s^2} \end{align*}

    Ideal Damper
    \begin{align*} \large \frac{F}{x} &= f_v s & \qquad \large \frac{x}{F} &= \frac{1}{f_v s} \end{align*}

    Ideal Spring
    \begin{align*} \large \frac{F}{x} &= K & \qquad \large \frac{x}{F} &= \frac{1}{K} \end{align*}
    69
    Voiceover

    Nise Summary

    Electrical components



    Figure 16


    71
    Voiceover

    Mechanical rotational components


    Figure 18
    73
    Voiceover

    Parallel analogue



    Figure 18: Mechanical parallel analogue
    60
    Voiceover

    Impedance and Admittance: Mechanical


    Ideal Mass
    \begin{align*} \large v &= \frac{p}{m} & \frac{\mathrm{d}p}{\mathrm{d}t} &= F \end{align*}

    Ideal Damper
    \begin{align*} \large F &= f_v v \end{align*}

    Ideal Spring
    \begin{align*} \large F &= K x & \frac{\mathrm{d}x}{\mathrm{d}t} &= v \end{align*}
    62
    Voiceover

    Impedance and Admittance: Mechanical


    Ideal Mass
    \begin{align*} \large \frac{F}{v} &= m s & \large \frac{v}{F} &= \frac{1}{m s} \end{align*}

    Ideal Damper
    \begin{align*} \large \frac{F}{v} &= f_v & \large \frac{v}{F} &= \frac{1}{f_v} \end{align*}

    Ideal Spring
    \begin{align*} \large \frac{F}{v} &= \frac{K}{s} & \large \frac{v}{F} &= \frac{s}{K} \end{align*}
    64
    Voiceover

    Impedance and Admittance: Rotational


    Ideal Inertia
    \begin{align*} \large \omega &= \frac{p}{J} & \qquad s p &= T \end{align*}

    Ideal Damper
    \begin{align*} \large T &= D \omega \end{align*}

    Ideal Spring
    \begin{align*} \large T &= K \theta & \qquad s \theta &= \omega \end{align*}
    66
    Voiceover

    Impedance $Z_M$ and Admittance $Y_M$: Electrical


    Ideal Inductor
    \begin{align*} \large \frac{V}{q} &= L s^2 & \qquad \frac{q}{V} &= \frac{1}{L s^2} \end{align*}

    Ideal Resistor
    \begin{align*} \large \frac{V}{q} &= R s & \qquad \frac{q}{V} &= \frac{1}{R s} \end{align*}

    Ideal Capacitor
    \begin{align*} \large \frac{V}{q} &= \frac{1}{C} & \qquad \frac{q}{V} &= C \end{align*}
    68
    Voiceover

    Impedance and Admittance: Rotational


    Ideal Inertia
    \begin{align*} \large \frac{T}{\theta} &= J s^2 & \large \qquad \frac{\theta}{T} &= \frac{1}{J s^2} \end{align*}

    Ideal Damper
    \begin{align*} \large \frac{T}{\theta} &= D s & \large \qquad \frac{\theta}{T} &= \frac{1}{D s} \end{align*}

    Ideal Spring
    \begin{align*} \large \frac{T}{\theta} &= K & \large \qquad \frac{\theta}{T} &= \frac{1}{K} \end{align*}
    70
    Voiceover

    Mechanical translational components


    Figure 17

    72
    Voiceover

    Series analogue


    Figure 19: Mechanical series analogue
  • 75
    Voiceover

    Conservation of power


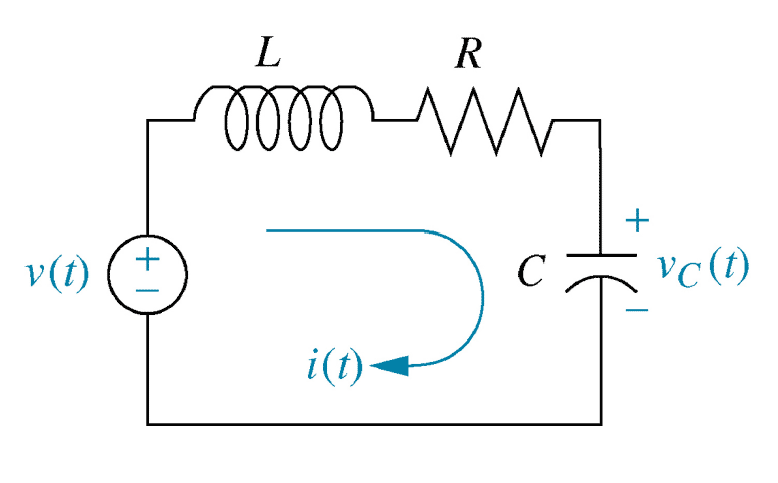    Figure 20


    Conservation of power
    \begin{align*} \large V_L I_L + V_R I_R + V_C I_C &= V_{in} I_{in} \end{align*}
    77
    Voiceover

    Kirchhoff’s laws


    Kirchhoff's Voltage Law (KVL)The voltages around a closed loop sum to zero.
    \begin{align*} \large \sum V_{in} - \sum V_{out} &= 0 \end{align*}

    Kirchhoff’s Current Law (KCL) The currents at an ideal node sum to zero
    \begin{align*} \large \sum I_{in} - \sum I_{out} &= 0 \end{align*}

    79
    Voiceover

    Interaction


    \begin{align*} \large V_L + V_R + V_C & \large = V_{in} \qquad \qquad \qquad \qquad (KVL) \\ \large \frac{V_L}{I_{in}} + \frac{V_R}{I_{in}} + \frac{V_c}{I_{in}} &= \large \frac{V_{in}}{I_{in}} \\ \large \frac{V_L}{I_L} + \frac{V_R}{I_R} + \frac{V_c}{I_C} &= \large \frac{V_{in}}{I_{in}} \\ \end{align*} \begin{align*} L s + R + \frac{1}{C s} &= \frac{V_{in}}{I_{in}} \\ \frac{I_{in}}{V_{in}} &= \frac{1}{L s + R + \frac{1}{C s}} \\ \frac{I_{in}}{V_{in}} &= \frac{s}{L s^2 + R s + \frac{1}{C}} \\ \end{align*}

    74
    Voiceover

    Chapter 2 - Interaction

    Electric circuit


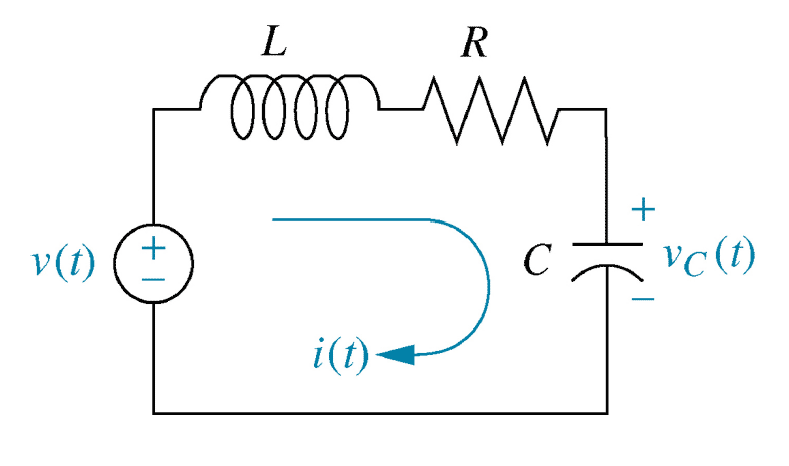    Figure 19

    Impedances
    \begin{align*} \large \frac{V_L}{I_L} &= L s & \qquad \large \frac{V_R}{I_R} &= R & \qquad \large \frac{V_C}{I_C} &= \frac{1}{C s} \end{align*}
    76

    Derivation of a Transfer Function from Kirchhoff's voltage law

    78
    Voiceover

    Interaction


    Conservation of power
    \begin{align*} \large V_L I_L + V_R I_R + V_C I_C &= \large V_{in} I_{in} \end{align*}

    Kirchhoff’s Laws
    \begin{align*} \large I_L &= I_R = I_C = I_{in} \qquad\qquad {KCL} \end{align*}

    \begin{align*} \large \implies & (V_L + V_R + V_C) I_{in} = V_{in} I_{in} \\ &&\\ \implies I_{in} &= 0 \qquad \text{ or } \\ & V_L + V_R + V_C = V_{in} \qquad\qquad {KVL} \end{align*}
    80
    Voiceover

    LRC Transfer Function



    Figure 21

    \begin{align*} \large \frac{I_{in}}{V_{in}} &= \frac{s}{L s^2 + R s + \frac{1}{C}} \\ \end{align*}
  • 82
    Voiceover

    Nodal Analysis

    1. Replace all passive components (L,R,C) with their admittances ($Y(s)$).
    2. Replace all sources and time variables with their Laplace transforms.
    3. Replace transformed voltage sources with transformed current sources.
    4. Write Kirchhoff's Current Law at each node.
    5. Solve the simultaneous equations for the output.
    6. Form the transfer function.




    (Nise, pp 54–56 / 51–53)
    84
    Voiceover

    Laplace transform of the input

    The input is a step of 4 V at time $t = 0$.
    From the table of transforms, a unit step is \begin{align*} H(s) &= \frac{1}{s} \end{align*}
    Using the linearity theorem, the input is therefore \begin{align*} V(s) &= 4 H(s) = \frac{4}{s} \end{align*} Now find $I(s)$.
    86
    Voiceover

    Inverse Laplace transform

    \begin{align*} I(s) &= \frac{4}{s^2 + 2 s + 2} \end{align*} Reformat the equation to match the tables of transforms.

    Complete the square. \begin{align*} (s+1)^2 = s^2 + 2 s + 1 &\implies& (s+1)^2 + 1 = s^2 + 2s + 2 \end{align*} \begin{align*} \therefore I(s) &= \frac{4}{(s+1)^2 + 1} \end{align*}
    Now use the frequency shift theorem.
    88
    Voiceover

    Step response
    \begin{align*} I(s) &= \frac{4}{s^2 + 2 s + 2} &\qquad \text{c.f. } \frac{k \omega_0^2}{s^2 + 2 \zeta \omega_0 s + \omega_0^2} \\ &&\qquad \omega_0 = \sqrt{2} \qquad \zeta = \frac{1}{\sqrt{2}} \\ &&\\ I(t) &= 4 e^{-t} \sin t \end{align*}

    Figure 22
    90
    Voiceover

    Code for plotting $q(t)$ in Matlab or Octave

    figure(2)
    g_qV = tf(4,[1,2,2])
    step(g_qV)
    title('LRC: Charge versus time: 1/(s 2+2s+2) x 4/s')
    xlabel('t [s]')
    ylabel('q [C]')
    grid on


    Figure 24

    print -depsc ’LRC-q.eps’
    81
    Voiceover

    Mesh and Nodal Analysis

    Mesh Analysis

    1. Replace all passive components (L,R,C) with their impedances ($Z(s)$).
    2. Replace all sources and time variables with their Laplace transforms.
    3. Assume a transform current and current direction in each mesh.
    4. Write Kirchhoff's Voltage Law around each mesh.
    5. Solve the simultaneous equations for the output.
    6. Form the transfer function.




    (Nise, pp 51--52 / 49--51)
    83
    Voiceover

    Example: LRC

    Example: I(t) for LRC using impedences

    Find an expression for the current $I(t)$ in a LRC circuit with parameters: \begin{align*} L &= 1 \text{H} & R &= 2 \Omega & C &= 0.5 \text{F} & V(t) &= 4 \text{V if } t \gt 0 \end{align*} Start by finding the Admittance $Y(s)$. \begin{align*} \frac{I}{V}(s) &= \frac{1}{L s + R + \frac{1}{C s}} \\ & \\ &= \frac{s}{L s^2 + R s + \frac{1}{C}} \\ & \\ &= \frac{s}{s^2 + 2 s + 2} \end{align*} Now find $V(s)$.
    85
    Voiceover

    I(s)

    \begin{align*} I(s) &= \frac{I}{V}(s) \times V(s) \\ &\\ &= \frac{s}{s^2 + 2 s + 2} \times \frac{4}{s} \\ &\\ &= \frac{\require{cancel}\cancel{s}}{s^2 + 2 s + 2} \times \frac{4}{\require{cancel}\cancel{s}} \\ &\\ &= \frac{4}{s^2 + 2 s + 2} \end{align*}
    Now find $I(t)$.
    87
    Voiceover

    Frequency shift theorem

    \begin{align*} I(s) &= \frac{4}{(s+1)^2 + 1} \end{align*} \begin{align*} \text{Let } G(s) &= \frac{1}{s^2+1^2} & \implies & g(t) = \sin t \end{align*} \begin{align*} I(s) &= 4 G(s+1) & \implies & I(t) = 4 e^{-t} g(t) \end{align*}

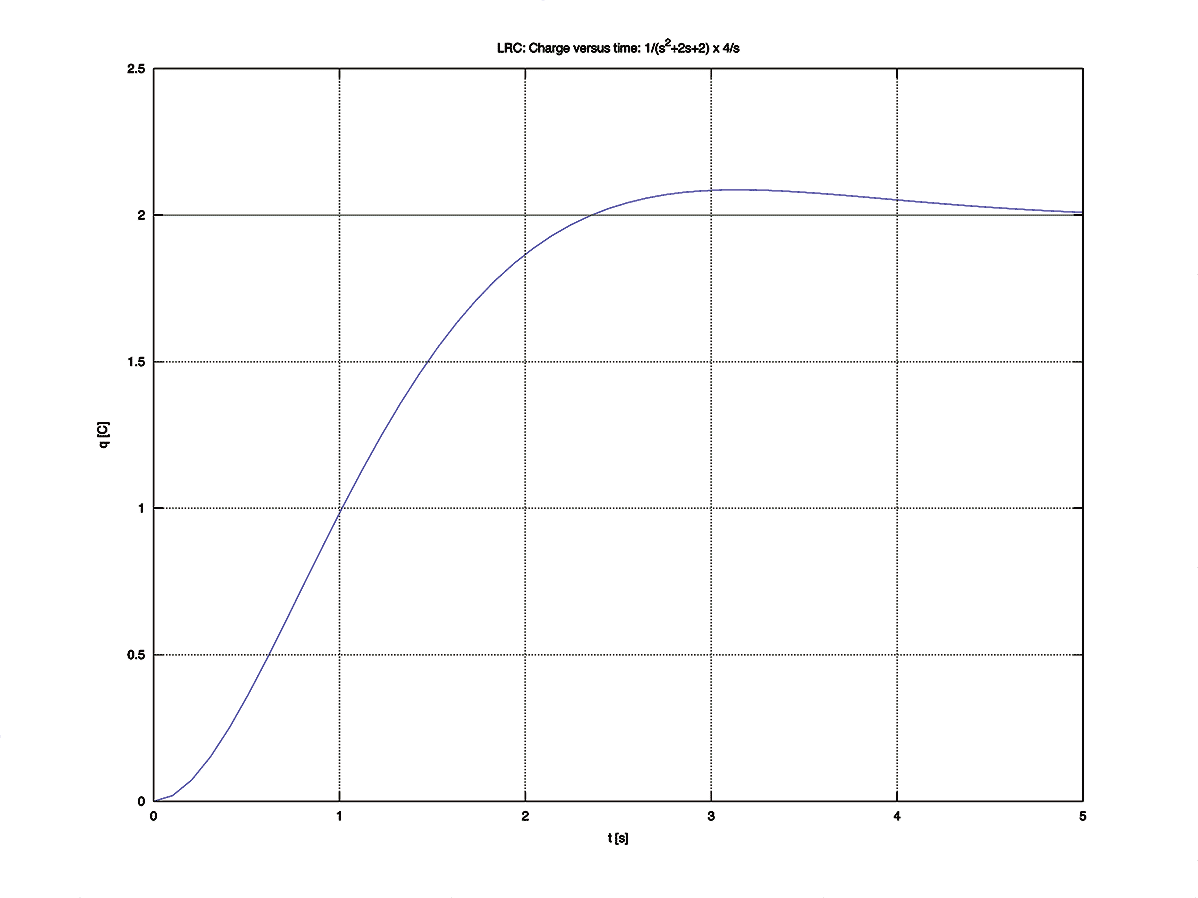
    $$ I(t) = 4 e^{-t} \sin t $$
    89
    Voiceover

    Code for plotting $I(t)$ in Matlab or Octave

    figure(1)
    g_iV = tf([4,0],[1,2,2])
    step(g_iV)
    title('LRC: Current versus time: s/(s 2+2s+2) x 4/s')
    xlabel('t [s]')
    ylabel('i [A]')
    grid on


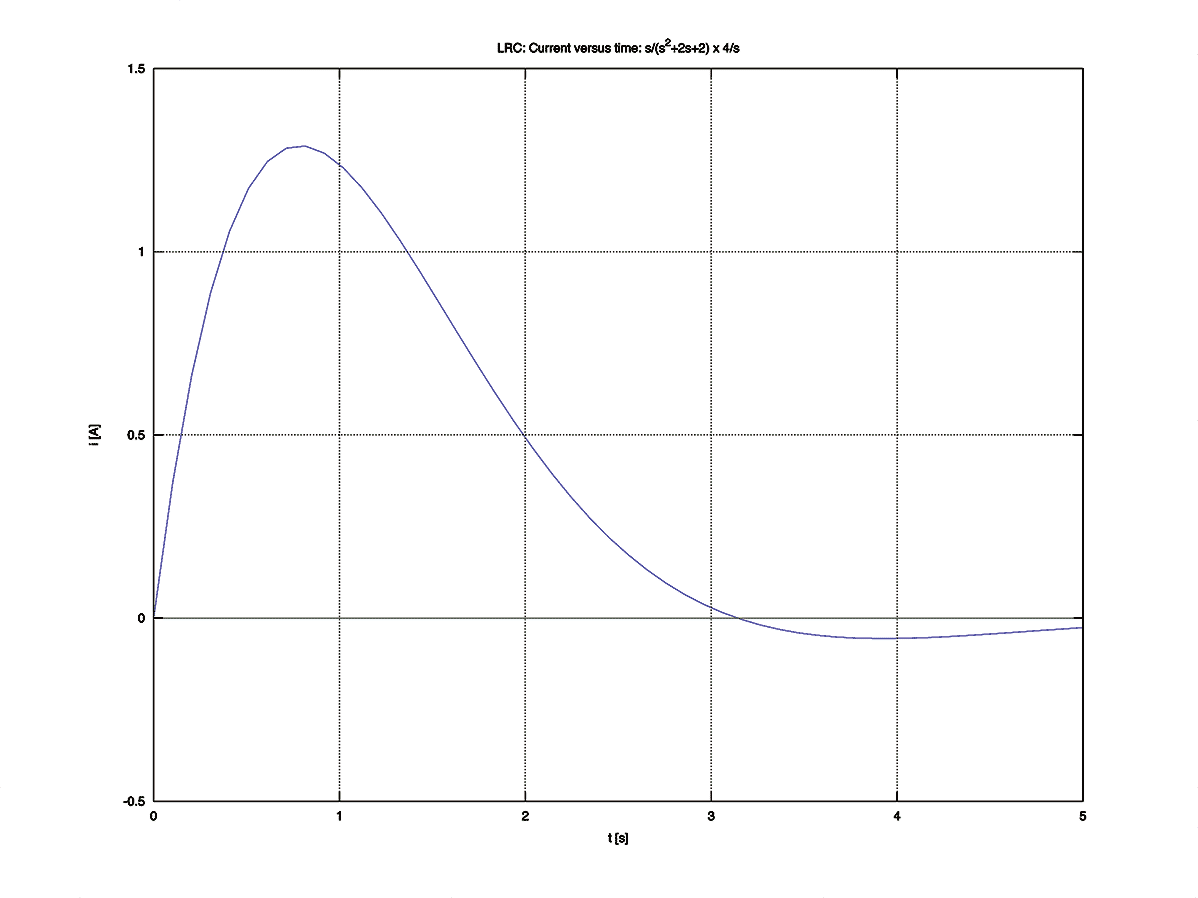    Figure 23

    print -depsc 'LRC-i.eps'



  • 92
    Voiceover

    Example: LRC (Cont.)

    Example: Mesh Analysis



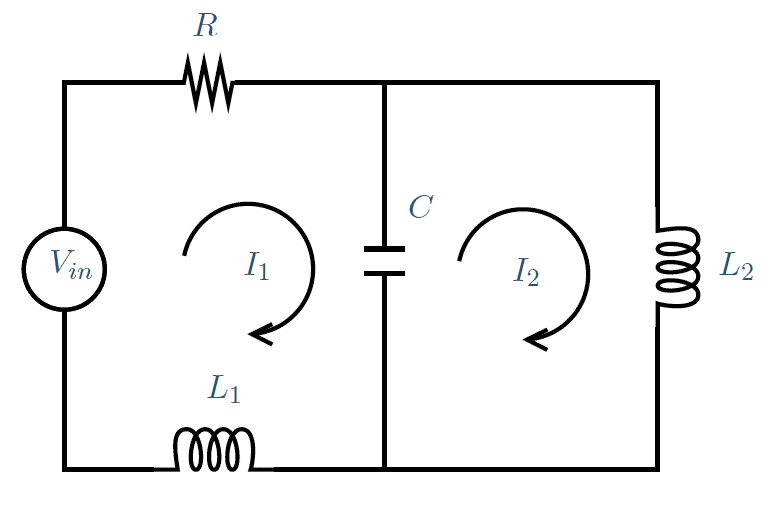    Figure 25

    Find an expression for $I_{in}(t)$ given $V_{in}(t)$.
    94
    Voiceover

    Collecting terms of $I_1$ and $I_2$

    NB: Unverified - check for errors!

      Loop 1 \begin{align*} \left(L_1 s + R_1 + \frac{1}{C s}\right) I_1 - \left(\frac{1}{C s}\right) I_2 &= V_{in} \end{align*}   Loop 2 \begin{align*} - \left(\frac{1}{C s}\right) I_1 + \left(L_2 s + \frac{1}{C s}\right) I_2 &= 0 \end{align*}
    96
    Voiceover

    Rearrange to form $V_{in}/I_{in}$

    NB: Unverified - check for errors! \begin{align*} L_1 s + R + \frac{1}{C s} - \left(\frac{1}{C s}\right) \frac{1}{L_2 C s^2 + 1} &= \frac{V_{in}}{I_{in}} \\ \frac{L_1 s (C s) (L_2 C s^2 +1)}{(C s) (L_2 C s^2 + 1} + \frac{R (C s) (L_2 C s^2 + 1)}{(C s) (L_2 C s^2 + 1)} +& \\ \cdots \frac{(L_2 C s^2 +1)}{(C s) (L_2 C s^2 + 1)} - \left(\frac{1}{C s}\right) \frac{1}{L_2 C s^2 + 1} &= \frac{V_{in}}{I_{in}} \\ \frac{Cs(L_1 L_2 s^3) + Cs(L_1 s) + Cs(L_2 R s^2) + Cs(R) + Cs(L_2 s)}{Cs(C L_2 s^2 + 1)} &= \frac{V_{in}}{I_{in}} \\ \frac{L_1 L_2 s^3 + L_2 R s^2 + (L_1 + L_2) s + R}{C L_2 s^2 + 1} &= \frac{V_{in}}{I_{in}} \\ \frac{C L_2 s^2 + 1}{L_1 L_2 s^3 + L_2 R s^2 + (L_1 + L_2) s + R} &= \frac{I_{in}}{V_{in}} \\ \end{align*}
    98
    Voiceover

    Matrices

    Matrices of transfer functions
    Structure resulting from a mesh analysis (electrical or mechanical) allows representation in matrix format.

      Loop 1 \begin{align*} \left(L_1 s + R_1 + \frac{1}{C s}\right) I_1 - \left(\frac{1}{C s}\right) I_2 &= V_{in} \end{align*}   Loop 2 \begin{align*} - \left(\frac{1}{C s}\right) I_1 + \left(L_2 s + \frac{1}{C s}\right) I_2 &= 0 \end{align*}
    \begin{align*} \begin{pmatrix} L_1 s + R + \frac{1}{C s} & - \frac{1}{C s} \\ -\frac{1}{C s} & L_2 s + \frac{1}{C s} \end{pmatrix} \begin{pmatrix} I_1 \\ I_2 \end{pmatrix} &= \begin{pmatrix} 1 \\ 0 \end{pmatrix} \begin{pmatrix} V_{in} \end{pmatrix} \end{align*}
    100
    Voiceover

    Outputs

    There are a number of outputs we may wish to derive, e.g.
    Current through an electrical component
    Voltage across an electrical component
    Force or torque generated by a mechanical component
    Translational or rotational displacement of a mass

    91
    Voiceover

    Example of using the Frequency Shift theorem

    Find $I(t)$ given \begin{align*} I(s) &= \frac{7}{(s+2)^2+9} \end{align*} $\qquad \qquad \qquad \text{Let} $ \begin{align*} G(s) &= \frac{3}{s^2+3^2} &\implies g(t) &= \sin 3 t \end{align*} \begin{align*} I(s) &= \frac{7}{3} G(s+2) \\ I(t) &= \frac{7}{3} e^{-2 t} g(t) \\ &= \frac{7}{3} e^{-2 t} \sin 3 t \end{align*}
    93
    Voiceover

    KVL for each loop

    NB: Unverified - check for errors!

      Loop 1 \begin{align*} R I_1 + \frac{1}{C s}(I_1-I_2) + L_1 s I_1 &= V_{in} \end{align*}   Loop 2 \begin{align*} \frac{1}{Cs}(I_2-I_1) + L_2 s I_2 &= 0 \end{align*}
    95
    Voiceover

    Eliminate $I_2$

    NB: Unverified - check for errors!

    From Loop 2 \begin{align*} \left(L_2 s + \frac{1}{C s}\right) I_2 &= \frac{1}{C s} I_1 \\ I_2 &= \frac{\frac{1}{C s} I_1}{L_2 s + \frac{1}{C s}} \\ I_2 &= \frac{I_1}{L_2 C s^2 + 1} \end{align*} Substitute for $I_2$ in Loop 1 \begin{align*} \left(L_1 s + R + \frac{1}{C s}\right) I_1 - \left(\frac{1}{C s}\right) \frac{I_1}{L_2 C s^2 + 1} &= V_{in} \end{align*}
    97
    Voiceover

    Finally get the current $I_{in}$

    \begin{align*} I_{in}(s) &= \frac{I_{in}}{V_{in}}(s) \times V_{in}(s) \\ &= \frac{C L_2 s^2 + 1}{L_1 L_2 s^3 + L_2 R s^2 + (L_1 + L_2) s + R} \times V_{in}(s) \end{align*}
    99
    Voiceover

    Cramer’s rule

    \begin{align*} \frac{I_1}{V_{in}}(s) &= \frac{ \left| \begin{matrix} 1 & -\frac{1}{C s} \\ 0 & L_2 s + \frac{1}{C s} \end{matrix} \right| } { \left| \begin{matrix} L_1 s + R + \frac{1}{C s} & - \frac{1}{C s} \\ -\frac{1}{C s} & L_2 s + \frac{1}{C s} \end{matrix} \right| } \end{align*} \begin{align*} \frac{I_2}{V_{in}}(s) &= \frac{ \left| \begin{matrix} L_1 s + R + \frac{1}{C s} & 1 \\ -\frac{1}{C s} & 0 \end{matrix} \right| } { \left| \begin{matrix} L_1 s + R + \frac{1}{C s} & - \frac{1}{C s} \\ -\frac{1}{C s} & L_2 s + \frac{1}{C s} \end{matrix} \right| } \end{align*}
  • 102
    Voiceover

    Voltage across a component

    Voltage across an electrical component can be obtained by finding the product of its impedance and current.
    For an electrical component in loop 1 that is not shared with any other loop,

    $\; V_{component} = Z_{component} \times I_1$
    $\Large \frac{V_{component}}{V_i} \normalsize = Z_{component} \times \Large \frac{I_1}{V_i}$

    For an electrical component shared between loop 1 and loop 2,

    $\; V_{component} = Z_{component} \times (I_1 - I_2)$

    $\Large \frac{V_{component}}{V_i} \normalsize = Z_{component} \times \Large \frac{I_1 - I_2}{V_i} \normalsize = Z_{component} \times \begin{pmatrix} \Large \frac{I_1}{V_i} - \frac{I_2}{V_i} \end{pmatrix} $
    104
    Voiceover

    Force or torque in a mechanical component

    The force generated by a mechanical component can be obtained from the product of its impedance and the displacement of the masses to which it is connected.
    For a spring or damper connected to mass 1 only,

    $\Large \frac{F_{component}}{F_i} \normalsize = Z_{m,component} \times \Large \frac{X_1}{F_i}$
    $\Large \frac{T_{component}}{T_i} \normalsize = Z_{m,component} \times \Large \frac{\theta_1}{T_i}$

    For a spring or damper connected to mass 1 and mass 2,

    $\Large \frac{F_{component}}{F_i} \normalsize = Z_{m,component} \times \Large \frac{X_1 - X_2}{F_i} \normalsize = Z_{m,component} \times \begin{pmatrix} \Large \frac{X_1}{F_i} - \frac{X_2}{F_i} \end{pmatrix}$
    $\Large \frac{T_{component}}{T_i} \normalsize = Z_{m,component} \times \Large \frac{\theta_1 - \theta_2}{T_i} \normalsize = Z_{m,component} \times \begin{pmatrix} \Large \frac{\theta_1}{T_i} - \frac{\theta_2}{T_i} \end{pmatrix}$
    106
    Voiceover

    Virtual mass

    Where a component is not connected to any mass (like the spring below), a symbolic virtual mass can be used with $m=0$.


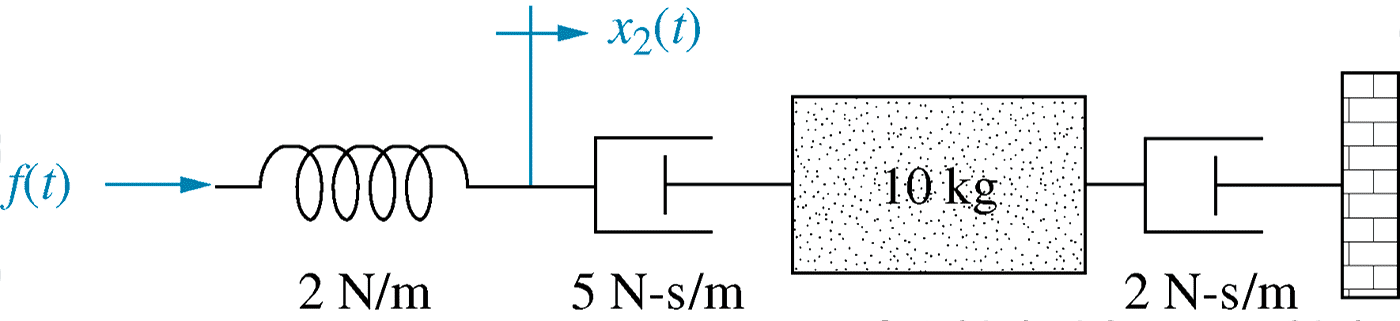    Figure 26

    This effectively incorporates Newton's III law into the technique of modelling by inspection (mechanical ``mesh'' analysis).
    108
    Voiceover

    Linearisation


    Figure 28




    101
    Voiceover

    Current through a component

    Current through an electrical component can be obtained from the Admittances of each loop to which it is connected.
    For an electrical component in loop 1 that is not shared with any other loop,

    $\; I_{component} = I_1$
    $\Large \frac{I_{component}}{V_i} \normalsize = \Large \frac{I_1}{V_i}$

    For an electrical component shared between loop 1 and loop 2,

    $\; I_{component} = I_1 - I_2$
    $\Large \frac{I_{component}}{V_i} = \frac{I_1 - I_2}{V_i} \normalsize = \Large \frac{I_1}{V_i} - \frac{I_2}{V_i} $
    103
    Voiceover

    Displacement of a mass

    The transfer function describing the translational or rotational displacement of a mass due to an applied force or torque is obtained directly from the mathematical model using Cramer’s rule.
    105
    Voiceover

    Using the definition of impedance


    \begin{align*} Z &= \frac{V}{I} & Z_m &= \frac{F}{X} & Z_m &= \frac{T}{\theta} \\\\ V &= Z \times I & F &= Z_m \times X & T &= Z_m \times \theta \\\\ \frac{V}{V_i} &= Z \times \frac{I}{V_i} & F &= Z_m \times \frac{X}{F_i} & T &= Z_m \times \frac{\theta}{T_i} \\ \end{align*}
    107
    Voiceover

    Gears


    Figure 27


    109
    Voiceover

    Summary.