Block Three


  • Chapter 12 - Design via state space


    Controller design
    Controllability
    Observability



  • 2
    Voiceover

    Plant representation

    A system with an $n^\text{th}$ order characteristic equation requires $n$ adjustable controller parameters: \begin{align*} s^n + a_{n-1} s^{n-1} + \ldots + a_1 s + a_0 &= 0 \end{align*} Henceforth, let us assume that the transmission matrix $\mathrm{D}$ is zero, and omit it from the state space representation. Let us also assume a single input $u$ and output $y$: \begin{align*} \underset{\sim}{\dot x} &= \mathrm{A}\underset{\sim}{x} + \mathrm{B} u & y &= \mathrm{C}\underset{\sim}{x} \end{align*}
    4
    Voiceover

    Control law
    \begin{align*} \large u &= \large r - \mathrm{K}\underset{\sim}{x} \end{align*}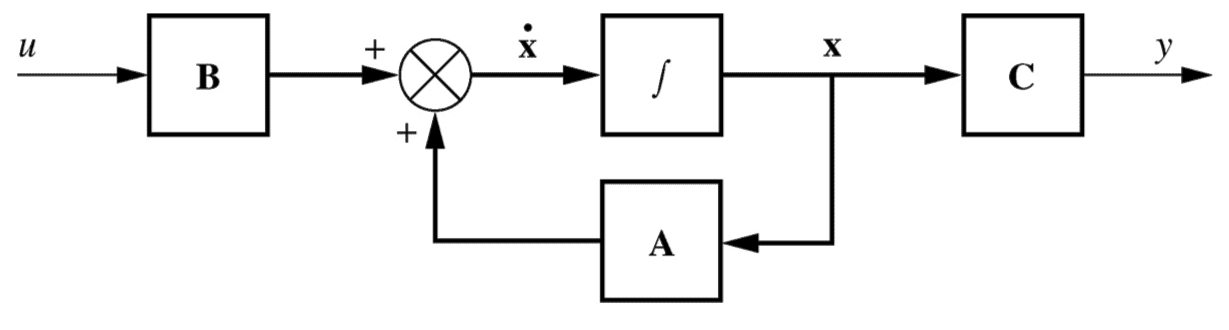


    6
    Voiceover

    Matrix dimensions

    \begin{align*} \underset{\sim}{\dot x} &= (\mathrm{A}-\mathrm{B}\mathrm{K})\underset{\sim}{x} + \mathrm{B} r & y &= \mathrm{C}\underset{\sim}{x} \end{align*} Matrix $\mathrm{K}$ must have as many columns as there are rows in $\underset{\sim}{x}$
    i.e. the number of states.

    Matrix $\mathrm{K}$ must have as many rows as there are columns in $\mathrm{B}$
    i.e. the number of inputs.

    For a SISO system, \begin{align*} \mathrm{K} &= \begin{pmatrix} k_1 & k_2 & \cdots & k_n \end{pmatrix} \end{align*} The dimensions can be easily adapted for MIMO systems.
    8
    Voiceover

    Pole placement with Matlab

    The Matlab command place() can calculate the matrix $\mathrm{K}$.



    $\tt {K = place(A,B,p)}$


    where $\tt{A}$ and $\tt{B}$ are the state and input matrices of the plant and $\tt{p}$ is an array of pole locations.

    uk.mathworks.com/help/
    10
    Voiceover

    Example

    Pole placement example

    A plant is defined as a state space system of equations: \begin{align*} \underset{\sim}{\dot x} &= \begin{pmatrix} -1 & 0 \\ 0 & -2 \end{pmatrix} \underset{\sim}{x} + \begin{pmatrix} 1 \\ 1 \end{pmatrix} u & y &= \begin{pmatrix} 1 & 1 \end{pmatrix} \underset{\sim}{x} \end{align*}

    Design a full state feedback controller such that the closed loop system has damping ratio $\zeta=0.8$ and natural frequency $\omega_n=1$ rad/s.
    12
    Voiceover

    Example: block diagram and equations



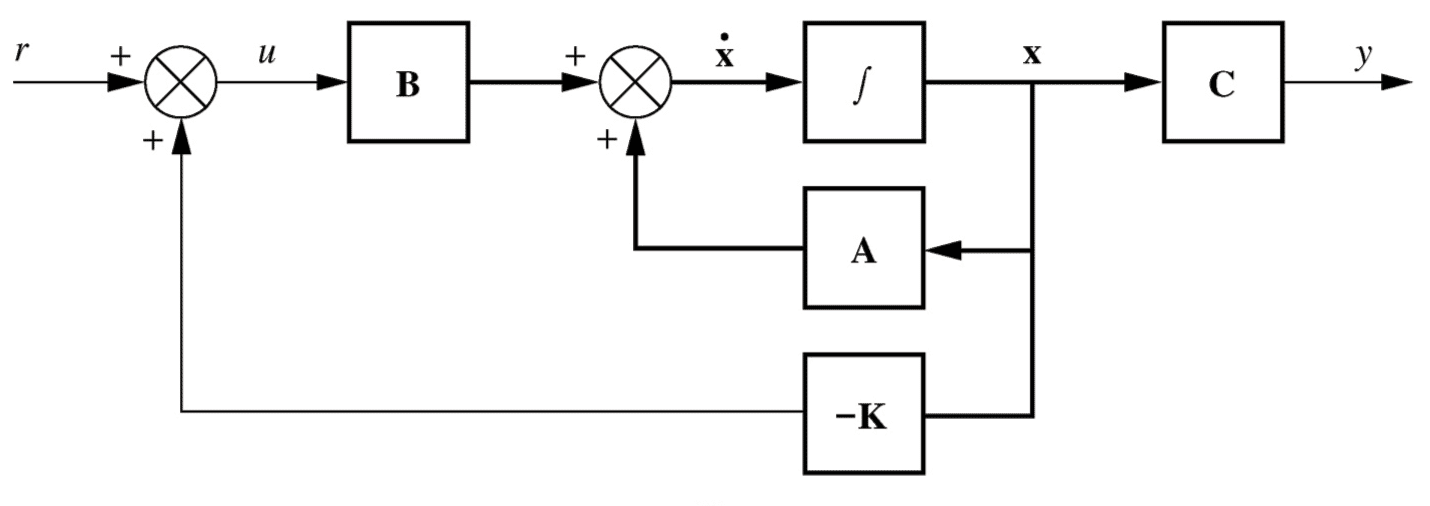
    Plant: \begin{align*} \underset{\sim}{\dot x} &= \mathrm{A}\underset{\sim}{x} + \mathrm{B}u & y &= \mathrm{C}\underset{\sim}{x} \end{align*} Control law: \begin{align*} u &= r - \mathrm{K}\underset{\sim}{x} \end{align*} Controlled system: \begin{align*} \underset{\sim}{\dot x} &= (\mathrm{A}-\mathrm{B}\mathrm{K})\underset{\sim}{x} + \mathrm{B}r & y &= \mathrm{C}\underset{\sim}{x} \end{align*} Controlled system poles: \begin{align*} |s\mathrm{I} - (\mathrm{A}-\mathrm{B}\mathrm{K})| &= 0 \end{align*} Examples continue on the next tab >
    1
    Voiceover

    Pole placement

    Controller design


    the $s$-plane, to meet a desired specification.

    Placement of $n$ poles requires a controller with $n$ parameters that can be adjusted.

    Pole placement makes use of the state space representation. It is assumed that all system states can be measured (or otherwise known1)
    1A Luenberger observer can be constructed using a similar method to pole placement.
    3
    Voiceover

    State feedback

    Figure 12.2a, p666 / 652

    5
    Voiceover

    System equations

    \begin{align*} \underset{\sim}{\dot x} &= \mathrm{A}\underset{\sim}{x} + \mathrm{B} u & y &= \mathrm{C}\underset{\sim}{x} \\ \\ u &= r - \mathrm{K}\underset{\sim}{x} \\ \\ \underset{\sim}{\dot x} &= \mathrm{A}\underset{\sim}{x} + \mathrm{B} (r-\mathrm{K}\underset{\sim}{x}) \\ \\ \underset{\sim}{\dot x} &= (\mathrm{A}-\mathrm{B}\mathrm{K})\underset{\sim}{x} + \mathrm{B} r & y &= \mathrm{C}\underset{\sim}{x} \end{align*}
    7
    Voiceover

    State transition matrix

    The state transition matrix for the controlled system can be calculated in a similar manner to the uncontrolled plant.

    Uncontrolled plant \begin{align*} \underset{\sim}{\dot x} &= \mathrm{A}\underset{\sim}{x} + \mathrm{B}\underset{\sim}{u} & y &= \mathrm{C}\underset{\sim}{x} \\ \Phi(s) &= (s\mathrm{I}-\mathrm{A})^{-1} \end{align*} Controlled system \begin{align*} \underset{\sim}{\dot x} &= (\mathrm{A}-\mathrm{B}\mathrm{K})\underset{\sim}{x} + \mathrm{B}\underset{\sim}{r} & y &= \mathrm{C}\underset{\sim}{x} \\ \Phi(s) &= \left(s\mathrm{I}-(\mathrm{A}-\mathrm{B}\mathrm{K})\right)^{-1} \end{align*} The controlled system poles are therefore located at \begin{align*} |s\mathrm{I}-(\mathrm{A}-\mathrm{B}\mathrm{K})| &= 0 \end{align*}
    9
    Voiceover

    The most difficult part ...

    The mathematics of pole placement is relatively easy.

    Determining where to place the poles is harder. This requires your engineering insight and understanding of the system requirements to develop an appropriate controller specification. Your knowledge of the $s$-plane should guide you.

    Decisions about where to place the poles will have consequences for actuator requirements, and hence cost and/or efficiency implications.

    As a rule of thumb, the further you try to move poles from their natural locations, the greater the power requirements.
    11
    Voiceover

    Example: procedure

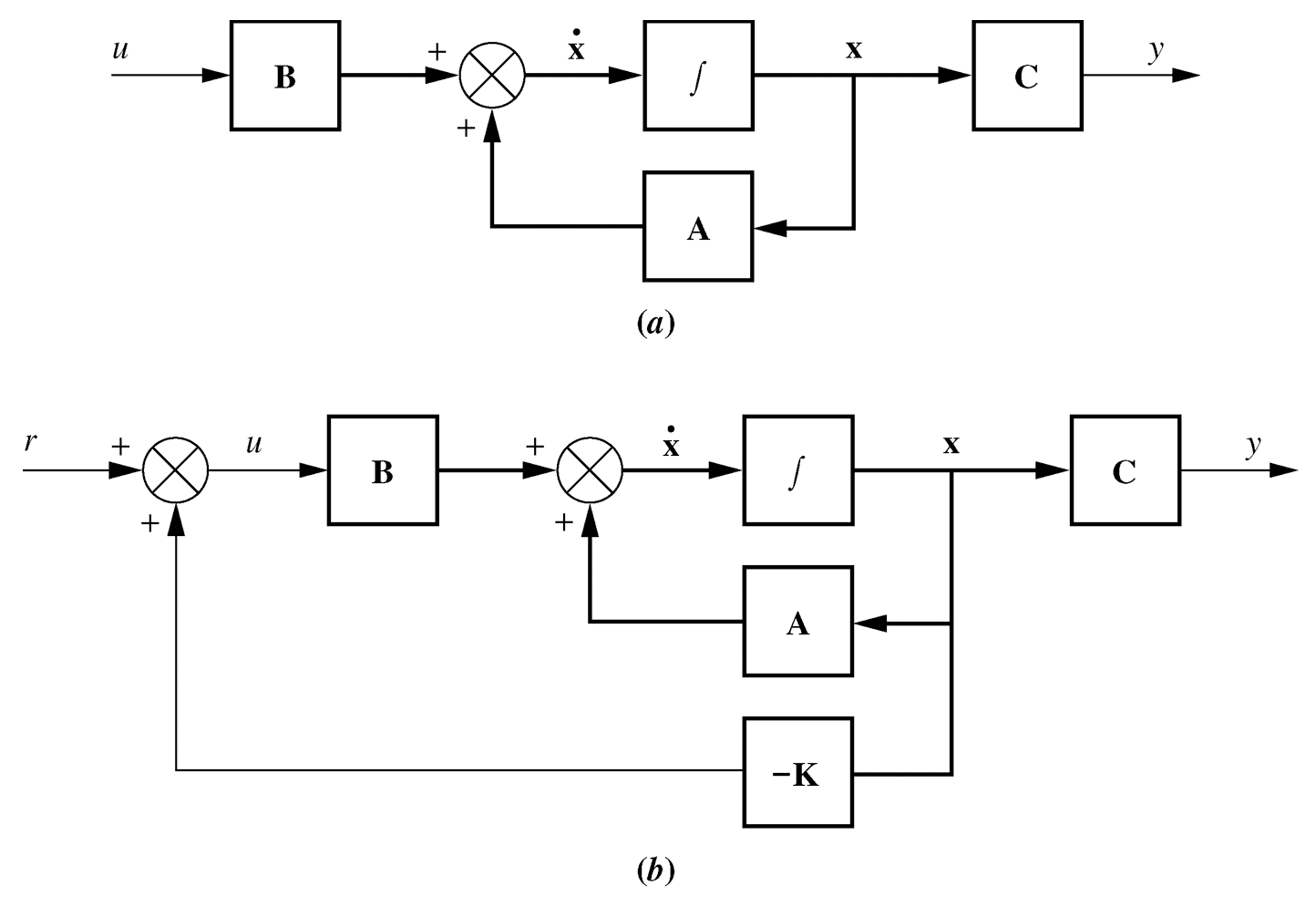
    1. Draw a block diagram of the controller structure

    2. Derive the system equations (plant and control law)

    3. Find the characteristic equation

    4. Develop a target specification and its characteristic equation i.e. determine the target pole locations

    5. Equate coefficients to map the controlled system to the target

    6. Solve to find the controller gain matrix $\mathrm{K}$

    7. Verify



  • 14
    Voiceover

    Example: target characteristic equation

    Controlled system characteristic equation: \begin{align*} s^2 + (k_1+k_2+3)s + 2+2k_1+k_2+ \require{cancel}\cancel{k_1k_2} -\cancel{k_1k_2} &= 0 \end{align*} Target specification: \begin{align*} \zeta& =0.8 & \omega_n &= 1\text{ rad/s} \end{align*} Target characteristic equation: \begin{align*} s^2 + 2\zeta\omega_n s + \omega_n^2 &= s^2 + 1.6 s + 1 = 0 \end{align*} Equating coefficients: \begin{align*} s^0&:& 1 &= 2+2k_1+k_2 \\ s^1&:& 1.6 &= k_1+k_2+3 \end{align*}
    16
    Voiceover

    Example: verification

    Target: \begin{align*} s^2 + 1.6 s + 1 &= 0 \end{align*} Controlled system: \begin{align*} s^2 + (k_1+k_2+3)s + 2+2k_1+k_2 &= 0 \end{align*} Substitute $k_1 = 0.4$ and $k_2 = -1.8$: \begin{align*} s^2 + (0.4-1.8+3)s + 2+2(0.4)+(-1.8) &= 0 \\ s^2 + 1.6 s + 1 &= 0 \end{align*} Thus the controlled system matches the target.
    18
    Voiceover

    A Controllable system (by inspection)


    Figure 12.6a, p673 / 658
    20
    Voiceover

    Controllability matrix

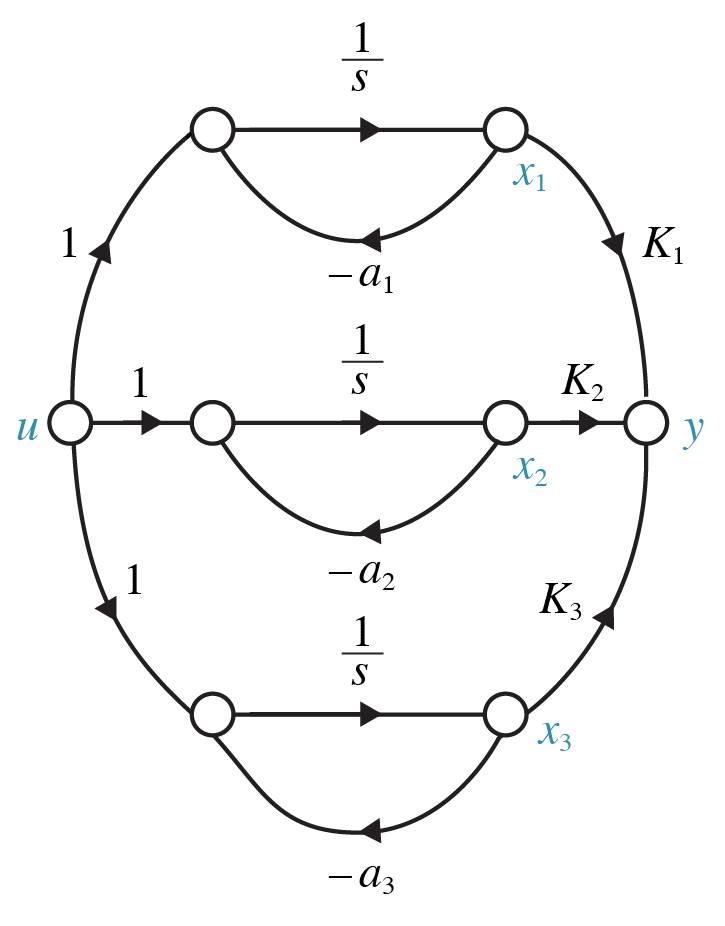
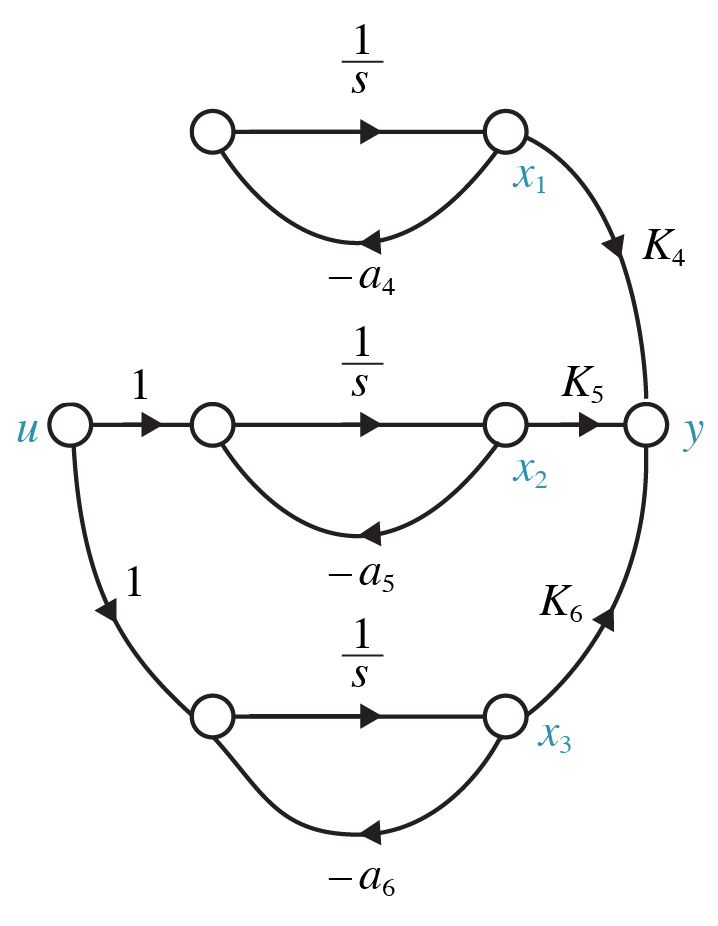
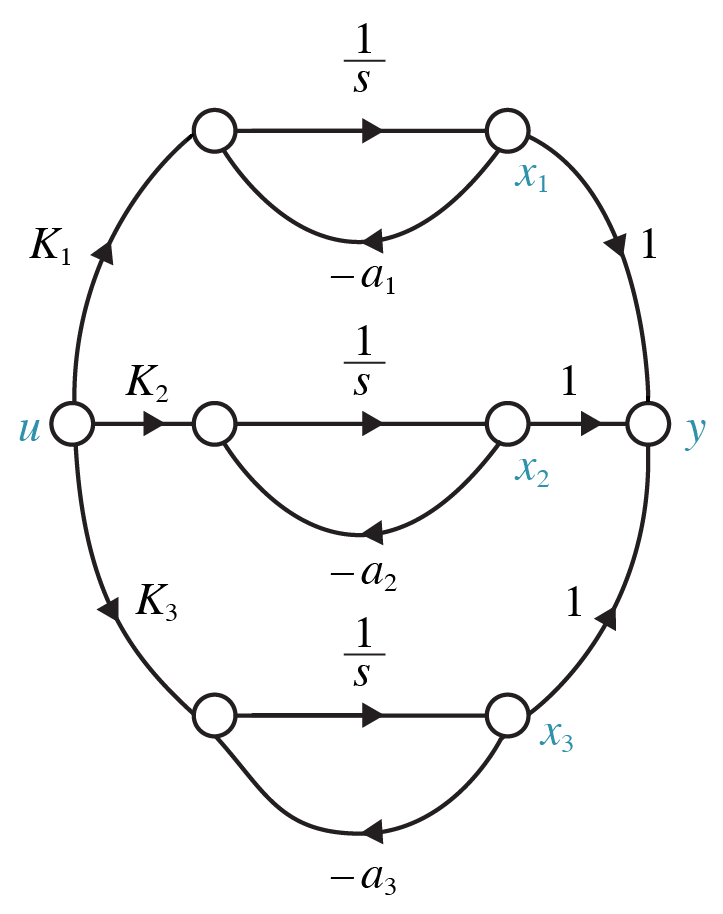
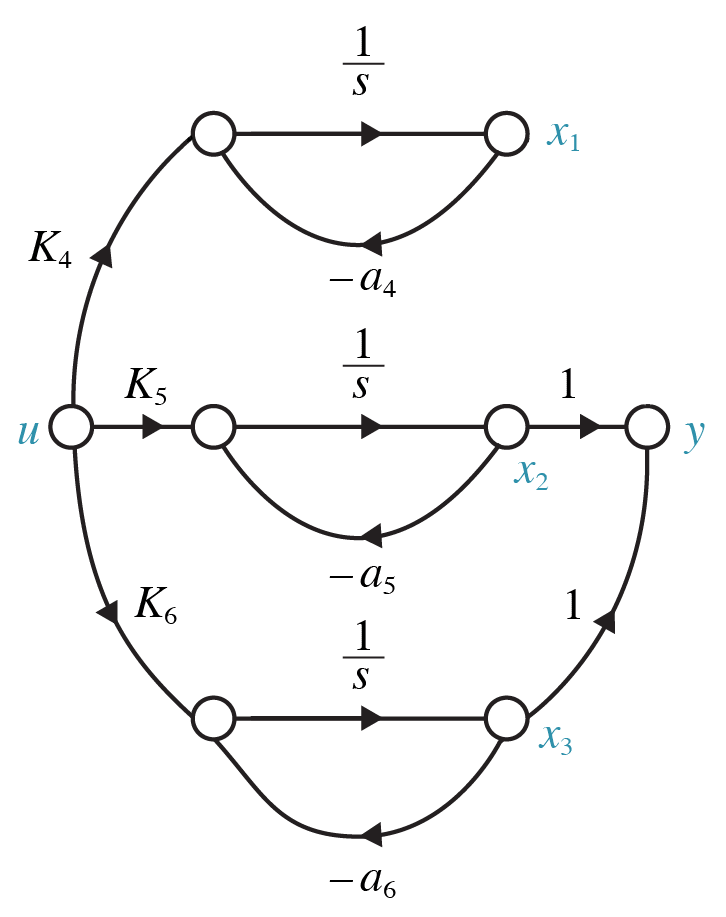
    For a system in parallel form (i.e. decoupled), the controllability of each state can be readily determined by inspection of the signal graph or state and input matrices $\mathrm{A}$ and $\mathrm{B}$.

    For a general state space system, its controllability can be determined by calculating the determinant of the controllability matrix. If the determinant is non-zero (i.e. the matrix is of full rank), the system is controllable. \begin{align*} \mathcal{C} &= \begin{pmatrix} \mathrm{B} & \mathrm{A}\mathrm{B} & \cdots & \mathrm{A}^{n-1}\mathrm{B} \end{pmatrix} \end{align*}
    13
    Voiceover

    Example: controlled system poles

    Controlled system poles: \begin{align*} |s\mathrm{I} - (\mathrm{A}-\mathrm{B}\mathrm{K})| &= 0 \end{align*} The system has two states ($\mathrm{A}$ is size $2\times 2$), hence two controller gains: \begin{align*} \mathrm{K} &= \begin{pmatrix} k_1 & k_2 \end{pmatrix} \\ \mathrm{B}\mathrm{K} &= \begin{pmatrix} 1 \\ 1 \end{pmatrix} \begin{pmatrix} k_1 & k_2 \end{pmatrix} = \begin{pmatrix} k_1 & k_2 \\ k_1 & k_2 \end{pmatrix} \end{align*} \begin{align*} |s\mathrm{I} - (\mathrm{A}-\mathrm{B}\mathrm{K})| &= \left| s\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} - \begin{pmatrix} -1 & 0 \\ 0 & -2 \end{pmatrix} + \begin{pmatrix} k_1 & k_2 \\ k_1 & k_2 \end{pmatrix} \right| = 0 \end{align*}
    \begin{align*} |s\mathrm{I} - (\mathrm{A}-\mathrm{B}\mathrm{K})| &= \left| s\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} - \begin{pmatrix} -1 & 0 \\ 0 & -2 \end{pmatrix} + \begin{pmatrix} k_1 & k_2 \\ k_1 & k_2 \end{pmatrix} \right| = 0 \end{align*} \begin{align*} \left| \begin{matrix} s+1+k_1 & k_2 \\ k_1 & s+2+k_2 \end{matrix} \right| &= 0 \end{align*} \begin{align*} (s+1+k_1)(s+2+k_2) - k_1 k_2 &= 0 \end{align*} \begin{align*} s^2 + (k_1+k_2+3)s + 2+2k_1+k_2+ \require{cancel} \cancel{k_1k_2} -\cancel{k_1k_2} &= 0 \end{align*}
    15
    Voiceover

    Example: solving for $\mathrm{K}$

    \begin{align*} s^1&:& 1.6 &= k_1+k_2+3 &\implies& k_1+k_2 = -1.4\\ &&\implies& k_2 = -1.4-k_1 \\ s^0&:& 1 &= 2+2k_1+k_2 &\implies& 1 = 2k_1+(-1.4-k_1)+2 \\ &&\implies& k_1 = 0.4 \end{align*} Hence $k_1=0.4$, $k_2=-1.8$ and the desired control law is: \begin{align*} u &= r - \begin{pmatrix} 0.4 & -1.8 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} \end{align*}
    17
    Voiceover

    Controllability

    Controllability

    In order to control the states, and hence outputs, of a system it is necessary that the system be controllable.

    Controllability is a test of whether it is possible to manipulate each state independently using the available inputs.
    19
    Voiceover

    An uncontrollable system (by inspection)


    Figure 12.6b, p 673 / 658
  • 22
    Voiceover

    An observable system (by inspection)


    Figure 12.15, p 690 / 674
    24
    Voiceover

    Observability matrix

    For a system in parallel form (i.e. decoupled), the observability of each state can be readily determined by inspection of the signal graph or state and output matrices $\mathrm{A}$ and $\mathrm{C}$.

    For a general state space system, its observability can be determined by calculating the determinant of the observability matrix. If the determinant is non-zero (i.e. the matrix is of full rank), the system is observable. \begin{align*} \mathcal{O} &= \begin{pmatrix} \mathrm{C} \\ \mathrm{C}\mathrm{A} \\ \vdots \\ \mathrm{C}\mathrm{A}^{n-1} \end{pmatrix} \end{align*}
    26
    Voiceover

    Integral action with pole placement

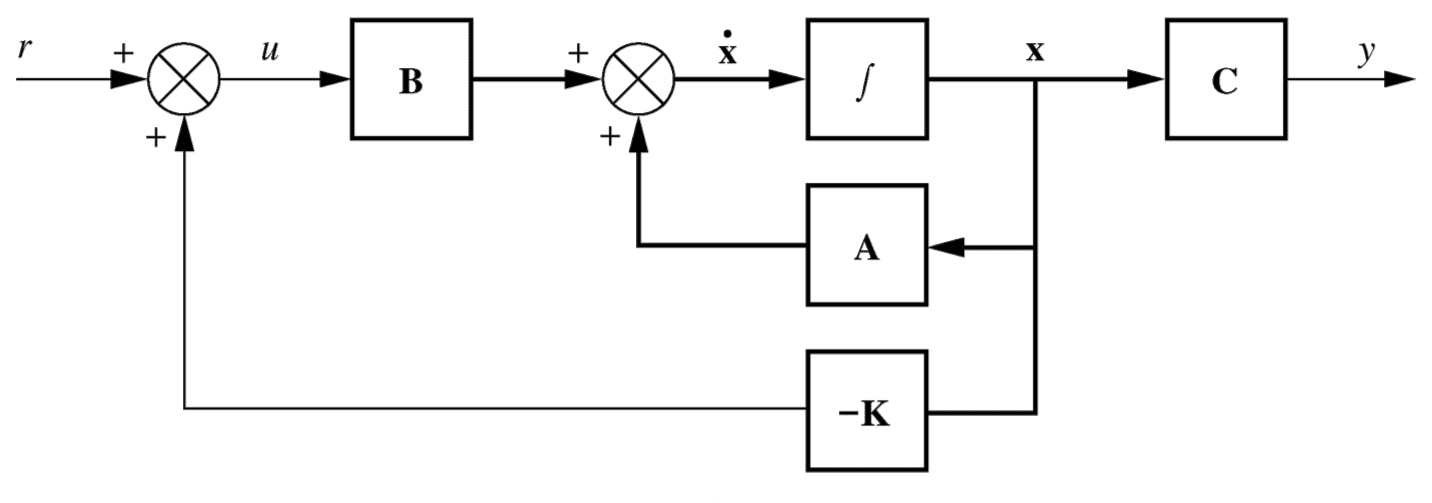
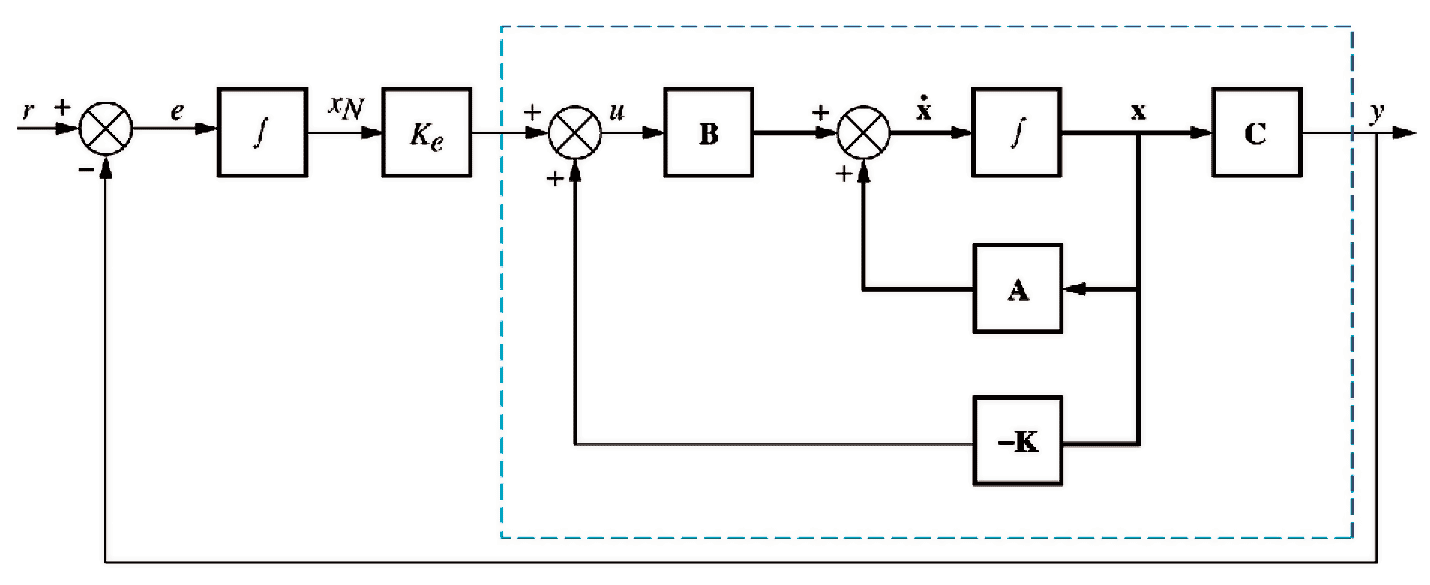    Figure 12.21, p700 / 684

    \begin{align*} \begin{pmatrix}\underset{\sim}{\dot x}\\\dot x_n\end{pmatrix} &= \begin{pmatrix} \mathrm{A}-\mathrm{B}\mathrm{K} & \mathrm{B}k_e \\ -\mathrm{C} & 0 \end{pmatrix} \begin{pmatrix} \underset{\sim}{x} \\ x_n \end{pmatrix} + \begin{pmatrix} \mathrm{0} \\ 1 \end{pmatrix} r \\ y &= \begin{pmatrix} \mathrm{C} & 0 \end{pmatrix} \begin{pmatrix} \underset{\sim}{x} \\ x_N \end{pmatrix} \end{align*}
    28
    Voiceover

    Example: transfer function
    \begin{align*} T(s) &= \mathrm{C} \mathrm{\Phi}(s) \mathrm{B} & \mathrm{\Phi}(s) &= \left(s\mathrm{I}-(\mathrm{A}-\mathrm{B}\mathrm{K})\right)^{-1} \end{align*} \begin{align*} \Phi(s) &= \frac{Adj \;\left(s\mathrm{I}-(\mathrm{A}-\mathrm{B}\mathrm{K})\right)}{|s\mathrm{I}-(\mathrm{A}-\mathrm{B}\mathrm{K})|} \end{align*} The determinant is known from previous analysis (the target characteristic equation): \begin{align*} |s\mathrm{I}-(\mathrm{A}-\mathrm{B}\mathrm{K})| &= s^2+2\zeta\omega_ns+\omega_n^2 = s^2+1.6s+1 \end{align*} The adjoint is the cofactor matrix transposed.
    30
    Voiceover

    Example: transfer function

    \begin{align*} T(s) &= \frac{ \begin{pmatrix} 1 & 1 \end{pmatrix} \begin{pmatrix} s+2+k_2 & -k_2 \\ -k_1 & s+1+k_1 \end{pmatrix} \begin{pmatrix} 1 \\ 1 \end{pmatrix} }{s^2+1.6s+1} \\ \\ &= \frac{ \begin{pmatrix} 1 & 1 \end{pmatrix} \begin{pmatrix} s+2 \\ s+1 \end{pmatrix} }{s^2+1.6s+1} \\ \\ &= \frac{(s+2)+(s+1)}{s^2+1.6s+1} \\ \\ &= \frac{2s+3}{s^2+1.6s+1} \end{align*}
    32
    Voiceover

    Example: result

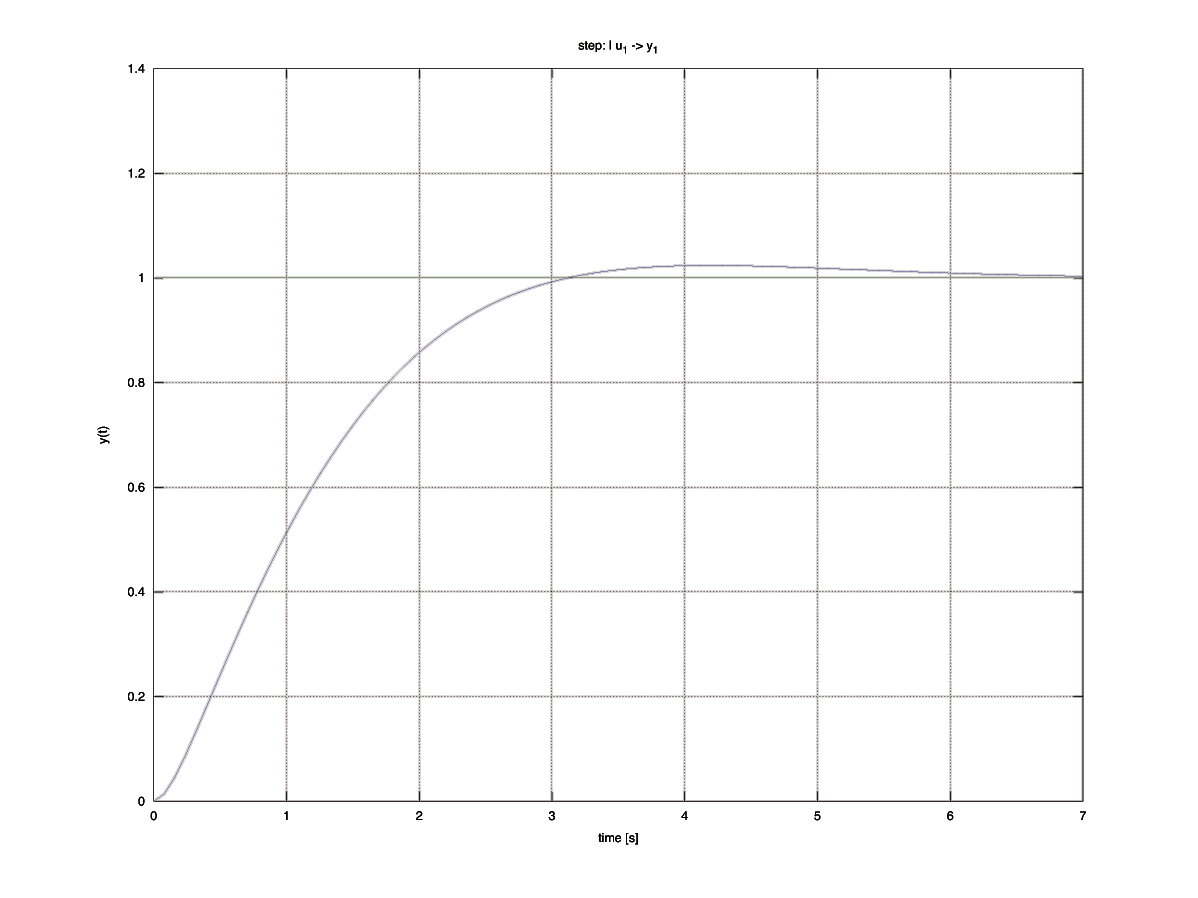
    The steady state error is non-zero in response to a step input. This suggests that the controller must be modified. The steady state error can be eliminated by introducing ``integral action'' into the forward path of the system, i.e. sufficient uncancelled poles at the origin based on the type of input.

    For a step input, 1 uncancelled pole at the origin will suffice. For a ramp input, 2 are required. For a parabolic input, we would need 3 uncancelled poles at the origin in the forward path.

    21
    Voiceover

    Observability

    Observability

    In order to monitor the states of a system it is necessary that the system be observable.

    Observability is a test of whether it is possible to monitor each state independently using the available outputs.
    23
    Voiceover

    An unobservable system (by inspection)


    Figure 12.15, p 690 / 674
    25
    Voiceover

    Integral control

    Elimination of steady state error

    Integral action can be integrated into a pole placement controller to ensure elimination of steady state error.

    Figure 12.21, p700 / 684
    27
    Voiceover

    Example (motivation)

    Example: motivation

    Consider the system designed by pole placement in the earlier example. \begin{align*} \underset{\sim}{\dot x} &= \begin{pmatrix} -1 & 0 \\ 0 & -2 \end{pmatrix} \underset{\sim}{x} + \begin{pmatrix} 1 \\ 1 \end{pmatrix} u & y &= \begin{pmatrix} 1 & 1 \end{pmatrix} \underset{\sim}{x} \\ u &= r - \begin{pmatrix} 0.4 & -1.8 \end{pmatrix} \underset{\sim}{x} \end{align*} If we calculate its transfer function $T(s)$ and apply the final value theorem, it will be apparent that the controlled system has a non-zero steady state input in response to a step input.
    29
    Voiceover

    Example: adjoint

    \begin{align*} \left(s\mathrm{I}-(\mathrm{A}-\mathrm{B}\mathrm{K})\right) &= \begin{pmatrix} s+1+k_1 & k_2 \\ k_1 & s+2+k_2 \end{pmatrix} \\ \end{align*}
    Cofactors: \begin{align*} \begin{pmatrix} s+2+k_2 & -k_1 \\ -k_2 & s+1+k_1 \end{pmatrix} \end{align*} Adjoint: \begin{align*} \begin{pmatrix} s+2+k_2 & -k_2 \\ -k_1 & s+1+k_1 \end{pmatrix} \end{align*}

    31
    Voiceover

    Steady state error

    \begin{align*} T(s) &= \frac{2s+3}{s^2+1.6s+1} & e(\infty) &= \lim_{s\rightarrow 0} s e(s) \end{align*} \begin{align*} e(s) &= r(s) - y(s) = r(s) - T(s) r(s) = \left(1-T(s)\right) r(s) \end{align*} \begin{align*} e(\infty) &= \lim_{s\rightarrow 0} s (1-T(s)) r(s) & r(s) &= \frac{1}{s} \\ &= \lim_{s\rightarrow 0} \cancel{s} (1-T(s)) \frac{1}{\cancel{s}} \\ &= 1 - \lim_{s\rightarrow 0} T(s) \\ &= 1 - \frac{2\cancelto{0}s+3}{\cancelto{0}{s}^2+1.6\cancelto{0}{s}+1} = 1-3 = -2 \end{align*}









  • 34
    Voiceover

    Example: procedure

    1. Draw a block diagram of the controller structure

    2. Derive the system equations (plant and control law)

    3. Find the characteristic equation

    4. Develop a target specification and its characteristic equation i.e. determine the target pole locations

    5. Equate coefficients to map the controlled system to the target

    6. Solve to find the controller gain matrix $\mathrm{K}$

    7. Verify
    36
    Voiceover

    Example: find the poles (eigenvalue problem)

    \begin{align*} \Delta &= \left| s\mathrm{I} - \begin{pmatrix} -1-k_1 & -k_2 & k_e \\ -k_1 & -2-k_2 & k_e \\ -1 & -1 & 0 \end{pmatrix} \right| \\ &= \left| \begin{matrix} s+1+k_1 & k_2 & -k_e \\ k_1 & s+2+k_2 & -k_e \\ 1 & 1 & s \end{matrix} \right| = 0 \\ \end{align*}
    Expanding along the third row (arbitrarily): \begin{align*} \Delta &= \left| \begin{matrix} k_2 & -k_e \\ s+2+k_2 & -k_e \end{matrix} \right| \\ &- \left| \begin{matrix} s+1+k_1 & -k_e \\ k_1 & -k_e \end{matrix} \right|\\ &+ s \left| \begin{matrix} s+1+k_1 & k_2 \\ k_1 & s+2+k_2 \end{matrix} \right| \\ \\ &= s^3+s^2(k_1+k_2+3)+s(2k_e+2k_1+k_2+2)+3k_e = 0 \end{align*}
    38
    Voiceover
    Example: mapping coefficients of $s$

    Controlled system: \begin{align*} s^3+s^2(k_1+k_2+3)+s(2k_1+k_2+2k_e+2)+3k_e &= 0 \end{align*} Target: \begin{align*} s^3+9.6s^2+13.8s+8 &= 0 \end{align*} Equating coefficients: \begin{align*} s^0&:& 8 &= 3 k_e &\implies& k_e = \frac{8}{3} \\ s^1&:& 13.8 &= 2k_1+k_2+2k_e+2 &\implies& k_2 = \frac{97}{15} - 2k_1 \\ s^2&:& 9.6 &= k_1 + k_2 + 3 &\implies& k_1 = -\frac{2}{15} \end{align*} Hence $k_1=-\frac{2}{15}$, $k_2=\frac{101}{15}$ and $k_e=\frac{8}{3}$.
    40
    Voiceover

    Step response


        
a=[-1,0;0,-2], b=[1;1], c=[1,1], d=0,
ke=8/3, k1=-2/15, k2=101/15, k=[k1,k2],
aa=[a-b*k,b*ke;-c,0], bb=[0;0;1], cc=[1,1,0],
g=ss(aa,bb,cc,d); step(g),
print -depsc 'figs/integral-pole-placement-step.eps'
    33
    Voiceover

    Example (design)

    Pole placement with integral action example

    A plant is defined as a state space system of equations: \begin{align*} \underset{\sim}{\dot x} &= \begin{pmatrix} -1 & 0 \\ 0 & -2 \end{pmatrix} \underset{\sim}{x} + \begin{pmatrix} 1 \\ 1 \end{pmatrix} u & y &= \begin{pmatrix} 1 & 1 \end{pmatrix} \underset{\sim}{x} \end{align*}

    Design a full state feedback controller such that the closed loop system has damping ratio $\zeta=0.8$, natural frequency $\omega_n=1$ rad/s and zero steady state error in response to a step input.

    35
    Voiceover

    Example: block diagram and equations




    Plant: \begin{align*} \underset{\sim}{\dot x} &= \mathrm{A}\underset{\sim}{x} + \mathrm{B}u & y &= \mathrm{C}\underset{\sim}{x} \end{align*} Control law: \begin{align*} u &= k_e x_N - \mathrm{K}\underset{\sim}{x} & \dot x_N &= r - y \end{align*}
    \begin{align*} \begin{pmatrix} \underset{\sim}{\dot x} \\ \dot x_N \end{pmatrix} &= \begin{pmatrix} \mathrm{A}-\mathrm{B}\mathrm{K} & \mathrm{B}k_e \\ -\mathrm{C} & 0 \end{pmatrix} \begin{pmatrix} \underset{\sim}{x} \\ x_N \end{pmatrix} + \begin{pmatrix} \underset{\sim}{0} \\ 1 \end{pmatrix} r \\ y &= \begin{pmatrix} \mathrm{C} & 0 \end{pmatrix} \end{align*}
    \begin{align*} \begin{pmatrix} \dot x_1 \\ \dot x_2 \\ \dot x_N \end{pmatrix} &= \begin{pmatrix} -1-k_1 & -k_2 & k_e \\ -k_1 & -2-k_2 & k_e \\ -1 & -1 & 0 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ x_N \end{pmatrix} + \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} r \\ y &= \begin{pmatrix} 1 & 1 & 0 \end{pmatrix} \end{align*}
    37
    Voiceover

    Example: target specification

    Controlled system characteristic equation: \begin{align*} s^3+s^2(k_1+k_2+3)+s(2k_e+2k_1+k_2+2)+3k_e &= 0 \end{align*} Target specification: \begin{align*} \zeta& =0.8 & \omega_n &= 1\text{~rad/s} & e_{step}(\infty) &= 0 \end{align*} Three poles must be placed. Placing the third pole 10 times further to the left than the target pair will avoid interference with the dominant dynamics: \begin{align*} (s^2+2\zeta\omega_ns+\omega_n^2)(s+10\sigma) &= 0 \\ \end{align*} The dominant pair are located at $s=-0.8\pm j0.6$, hence place the third pole at $s=-8$. The target becomes: \begin{align*} (s+1.6s+1)(s+8) &= s^3+9.6s^2+13.8s+8 = 0 \end{align*}
    39
    Voiceover

    Example: final controller


    \begin{align*} \mathrm{K} &= \frac{1}{15} \begin{pmatrix} -2 & 101 \end{pmatrix} & \qquad k_e &= \frac{8}{3} \end{align*}