

To help you work out what your current knowledge and skills are like here are some questions to try. The questions are grouped by topic, and each topic contains one “Basic” and one “Complex” question.
These questions are NOT A TEST they are for you to help work out which topics you should focus your energies on.
The questions are arranged by topic to make it easy to know where to find extra reading.
If you have no idea how to do a “Basic” question then you should go and read some comprehensive notes on the topic first, and then attempt some exercises. Links have been provided in the “Revision Topics Learning Plan” document. It is probably just a topic you’ve never studied, or one you studied a while ago. This is fine, it just means you have some things to learn still!
If you can do the “Basic” question but not the “Complex” one, or just struggled with the basic one then you will probably benefit from the same reading but feel free to move quickly over things you can already do. Even if you find a question easy, feel free to browse the online resources quickly anyway, it may be a useful reminder to help reinforce your existing knowledge.
Now for the questions!
Indices or Powers
(Basic) Simplify the powers in the following expression \[(2^3)^4+3 \times 3^2\] into a formula of the form \(2^a + 3^b\) for some constants \(a\) and \(b\).
(Complex) Simplify \[\frac{\sqrt{x}(yz)^2}{x^3y^{-3/2}}\] into the form \(x^ay^bz^c\) for numbers \(a\), \(b\) and \(c\).
Algebra: expanding/removing brackets
(Basic) Expand/remove the brackets in this expression: \[4x(3x-y)\]
(Complex) Expand the brackets and find all the solutions for \(x\) to this equation: \[(x+3)(x-3)=16\]
Algebra: re-arranging equations
(Basic) Re-arrange this equation to find the solution for \(x\): \[3x+15 = 6x + 3\]
(Complex) Make \(x\) the subject of this equation: \[y=\frac{1+x}{1-tx}\] (you may assume that \(y\) and \(t\) are both positive, if you need)
Algebra: simplifying and factorising
(Basic) Simplify this expression: \[5x-3w+r-2x+w\]
(Complex) Simplify this expression and then take out a common factor to factorise: \[3x^2+4xy-x^2-6xy\]
Trigonometric functions
(Basic) In the triangle below, which function of \(\theta\) is equal to \(\frac{y}{x}\)?
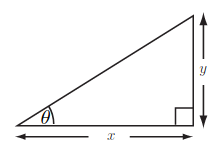
(Complex) If a right-angled triangle’s two shortest sides are \(5\) and \(12\), work out how long the longest side is, and give a formula for the smallest of the three angles inside the triangle using an inverse trigonometric function.