Week 5: Capacitance and Electric Fields

Wk 5

Capacitance and Electric Fields

Introduction

Capacitors and Capacitance

Alternating Voltages and Currents

The Effect of a Capacitor’s Dimensions

Electric Fields

Capacitors in Series and Parallel

Voltage and Current

Sinusoidal Voltages and Currents

Energy Stored in a Charged Capacitor

Circuit Symbols

Introduction

We noted earlier that an electric current represents a flow of charge

A capacitor can store electric charge and can therefore store electrical energy

Capacitors are often used in association with alternating currents and voltages

They are a key component in almost all electronic circuits

They are a key component in almost all electronic circuits
📷 Show Circuit Symbols
(continued)

– charge produces an electric field across the capacitor and a voltage across it

For a given capacitor the stored charge q is directly proportional to the voltage across it $V$

The constant of proportionality is the capacitance $C$ and thus

\begin{align*} \large C &= \frac{\large Q}{V} \end{align*}

If the charge is measured in coulombs and the voltage in volts, then the capacitance is in farads

Example – see Example 4.1 in course text. A 10 μF capacitor has 10 V across it. What quantity of charge is stored in it?
From above: \begin{align*} \large C &= \frac{\large Q}{V} \\ Q &= CV\\ &= 10\; ^5. 10\\ &= 100 \; \mu C \end{align*}

Capacitors and Capacitance

Capacitors consist of two conducting surfaces separated by an insulating layer called a dielectric

A simple capacitor circuit

– when switch is closed electrons flow from top plate into battery and from battery onto bottom plate
The Effect of a Capacitor’s Dimensions

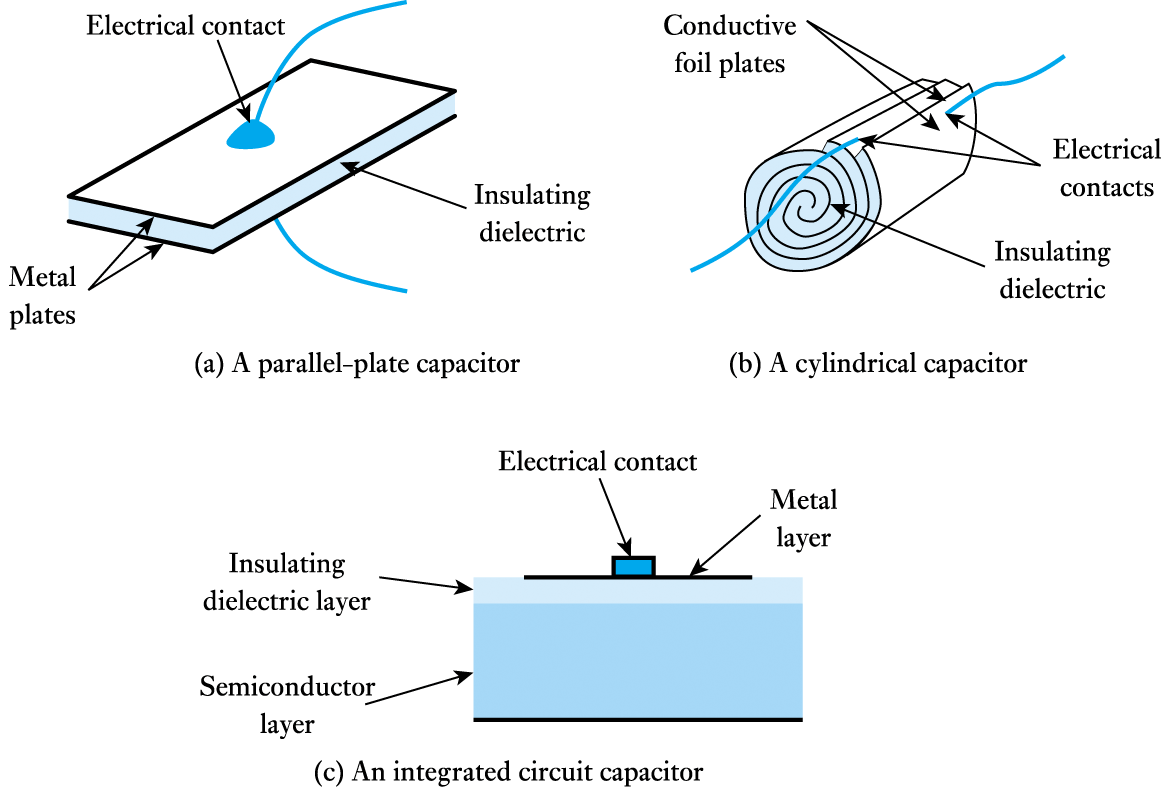
The capacitance of a capacitor is directly proportional to its area $A$, and inversely proportional to the distance between its plates d. Hence $$ \large C \; \propto \; A/d$$
– the constant of proportionality is the permittivity ε of the dielectric

– the permittivity is normally expressed as the product of the absolute permittivity ε0 and the relative permittivity εr of the dielectric used

\begin{align*} \large C &= \frac{\large \varepsilon A}{d} = \frac{\large \varepsilon _0 \varepsilon _r A}{d} \end{align*}

Alternating Voltages and Currents

A constant current cannot flow through a capacitor

–  however, since the voltage across a capacitor is proportional to the charge on it, an alternating voltage must correspond to an alternating charge, and hence to current flowing into and out of the capacitor

–  this can give the impression that an alternating current flows through the capacitor

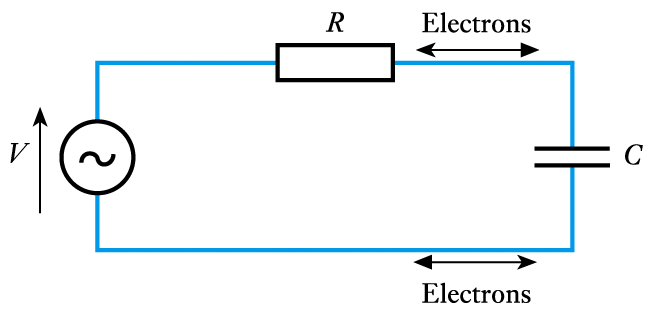
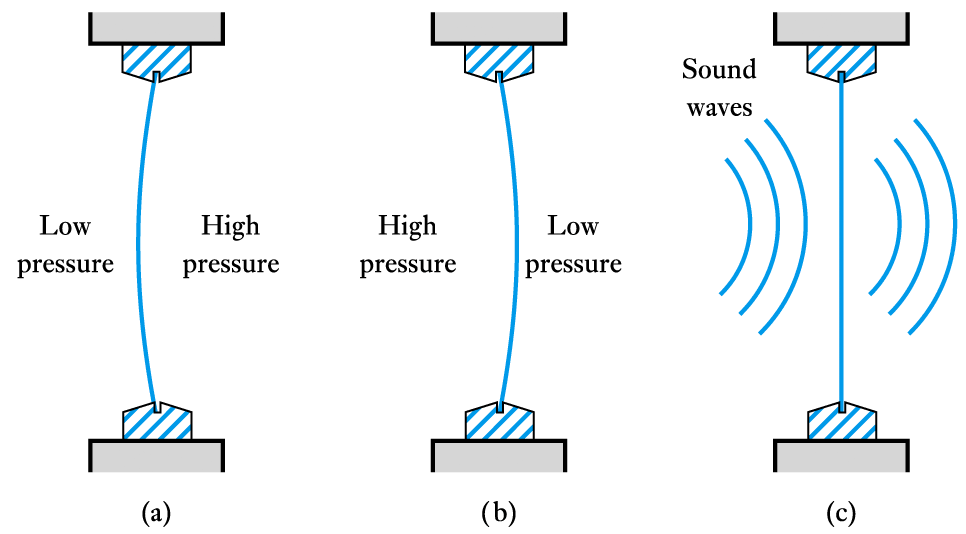
A mechanical analogy may help to explain this

–  consider a window - air cannot pass through it, but sound (which is a fluctuation in air pressure) can
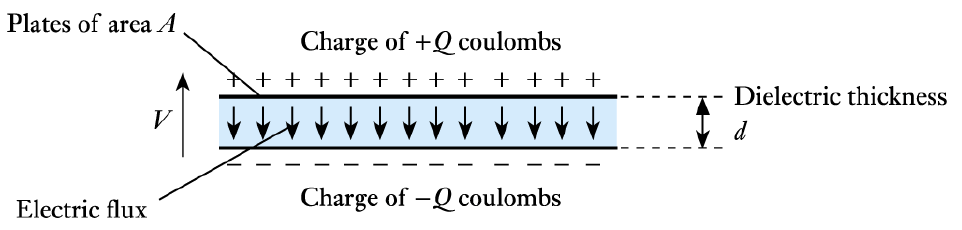
The force between positive and negative charges is described in terms of the electric flux linking them

– measured in coulombs (as for electric charge)

– a charge $Q$ will produce a total flux of $Q$ coulombs

We also define the electric flux density $D$ as the flux per unit area

In a capacitor we can almost always ignore edge effects, and

\begin{align*} \large D &= \frac{\large Q}{A} \end{align*}

Combining the earlier equations it is relatively easy to show that

\begin{align*} \Large \varepsilon &= \frac{\large D}{E} \end{align*}

Thus the permittivity of the dielectric within a capacitor is equal to the ratio of the electric flux density to the electric field strength

Electric Fields

The charge on the capacitor produces an electric field with an electric field strength E given by

\begin{align*} \large E &= \frac{\large V}{d} \end{align*}

the units of $E$ are volts/metre $(V/m)$

All insulating materials have a maximum value for the field strength that they can withstand

– the dielectric strength $E_m$

To produce maximum capacitance for a given size of capacitor we want d to be as small as possible

– however, as $d$ is decreased the electric field $E$ is increased

– if $E$ exceed $E_m$ the dielectric will

break down
– there is therefore a compromise between physical size and breakdown voltage
Capacitors in series

– consider a voltage $V$ applied across two capacitors in series

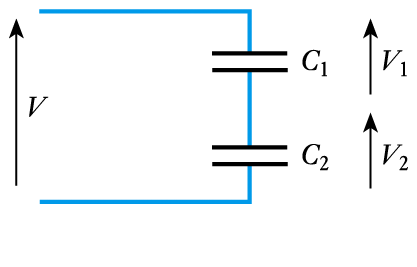
– the only charge that can be applied to the lower plate of $C_1$ is that supplied by the upper plate of $C_2$. Therefore the charge on each capacitor must be identical. Let this be $Q$, and therefore if a single capacitor $C$ has the same effect as the pair, then
\begin{align*} V =& V_1 + V_2 \\ \frac{Q}{C} =& \frac{Q}{C_1} + \frac{Q}{C_2} \\ \frac{1}{C}=& \frac{1}{C_1} + \frac{1}{C_2} \end{align*}

Capacitors in Series and Parallel

🎥 Watch a video on capacitors in series and in parallel - Adobe Flash video

Capacitors in parallel

– consider a voltage V applied across two capacitors

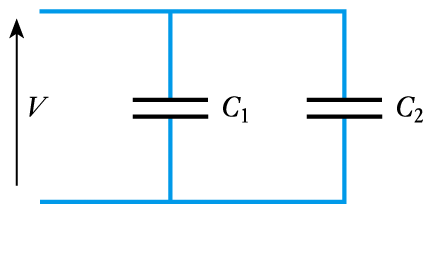
– then the charge on each is \begin{align*}Q_1 = VC_1 \qquad Q_2 = VC_2\end{align*}

– if the two capacitors are replaced with a single capacitor $C$ which has a similar effect as the pair, then
\begin{align*} \text{Charge stored on }C =& Q_1 + Q_2 \\ VC =& VC_1 + VC_2 \\ C=& C_1 + C_2 \end{align*}
(cont.)

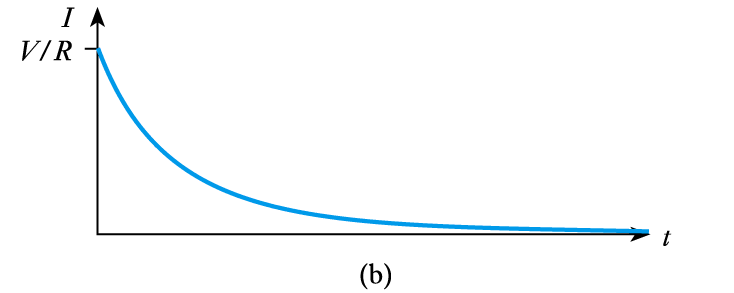
– as the capacitor charges:

$V_C$ increases

$V_R$ decreases

hence $I$ decreases

we have exponential behaviour

Time constant

– charging current is determined by $R$ and the voltage across it

– increasing $R$ will increase the time taken to charge $C$

– increasing $C$ will also increase time taken to charge $C$

– time required to charge to a particular voltage is determined by the product $CR$

– this product is the time constant T (greek tau)

See Computer Simulation Exercises 4.1 and 4.2 in the course text

Voltage and Current

The voltage across a capacitor is directly related to the charge on the capacitor

\begin{align*} \large V &= \frac{\large Q}{C} = \frac{1}{C} Idt \end{align*}

Alternatively, since Q = CV we can see that \begin{align*} \frac{ dQ}{dt} = C\frac{dV}{dt} \end{align*}
and since dQ/dt is equal to current, it follows that

\begin{align*} \large I &= C\frac{dV}{dt} \end{align*}

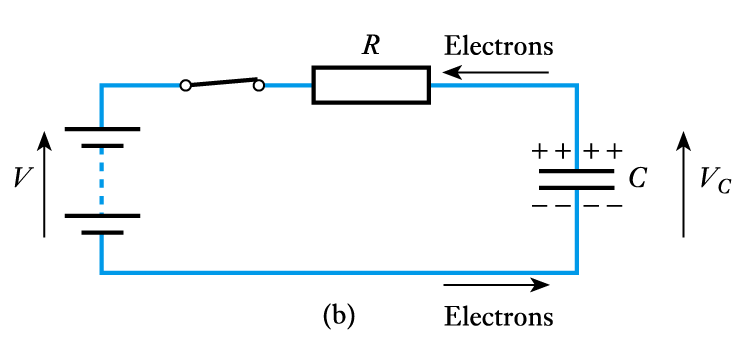
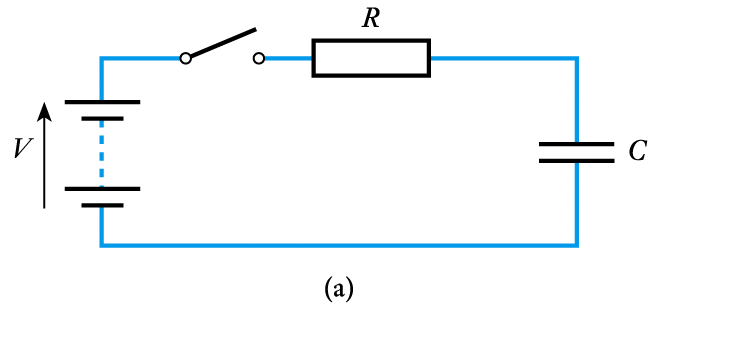
Consider the circuit shown here

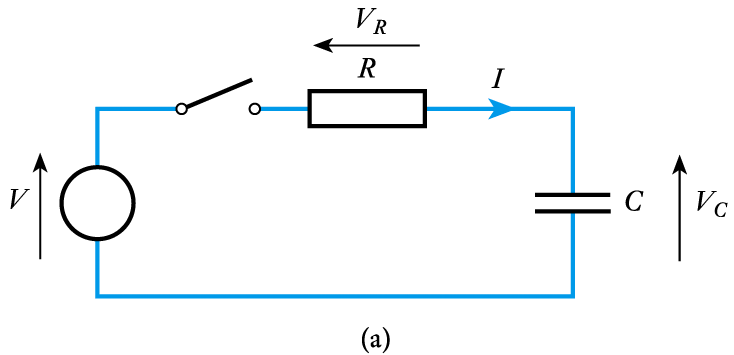
– capacitor is initially discharged

voltage across it will be zero

– switch is closed at $t = 0$

– $V_C$ is initially zero

hence $V_R$ is initially $V$

hence $I$ is initially $V/R$
Energy Stored in a Charged Capacitor

To move a charge $Q$ through a potential difference $V$ requires an amount of energy $QV$

As we charge up a capacitor we repeatedly add small amounts of charge $ \Delta Q$ by moving them through a voltage equal to the voltage on the capacitor

Since $Q = CV$, it follows that $ \Delta Q = C\Delta V$, so the energy needed $E$ is given by

\begin{align*} \large E = ^V_0 CVdV = \frac{1}{2}CV^2 \end{align*}

Alternatively, since $V = Q/C$

\begin{align*} \large E = \frac{1}{2} CV^2 = \frac{1}{2} C\frac{\;Q \; ^2}{C} = \frac{1}{2} \frac{Q^2}{C} \end{align*}

Example – see Example 4.7 in the course text Calculate the energy stored in a $10 \mu F$ capacitor when it is charged to $100 V$
From above:

\begin{align*} \large E = \frac{1}{2} CV^2 = \frac{1}{2} \cdot 10 \; ^5 \cdot 100^2 = 50 \; mJ \end{align*}

Sinusoidal Voltages and Currents

Consider the application of a sinusoidal voltage to a capacitor

– from above $I = C \; dV/dt$

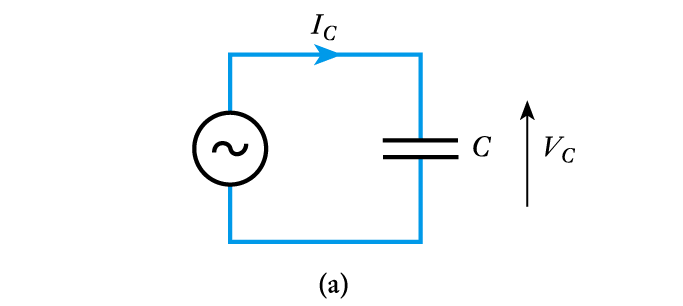
– current is directly proportional to the differential of the voltage

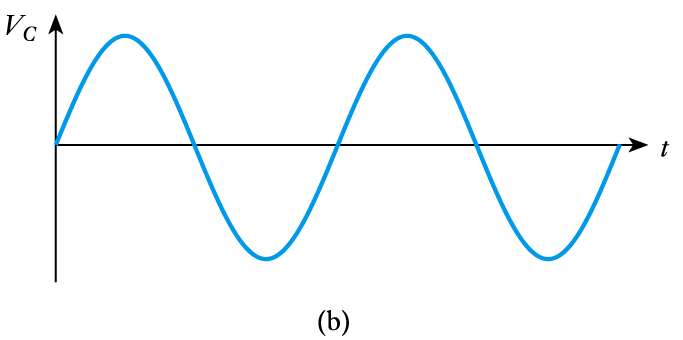
– the differential of a sine wave is a cosine wave

– the current is phase-shifted by 90° with respect to the voltage

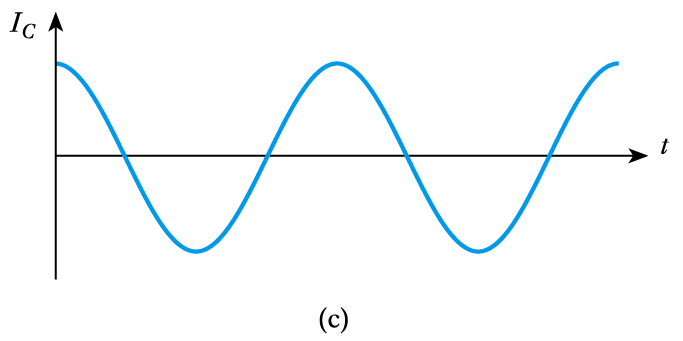
Since $I = C \; dV/dt$ the magnitude of the current is related to the rate of change of the voltage

– in sinusoidal voltages the rate of change is determined by the frequency

– hence capacitors are frequency dependent in their characteristics

We will return to look at frequency dependence in later lectures.
Further Study

🎥 Watch a further study video on energy storage in parallel capacitors - Adobe Flash video

The Further Study section at the end of Chapter 4 looks at the energy stored within capacitors and considers what happens when two charge capacitors are joined together.

Do the sums yourself, then watch the video to check your calculations.

We begin by reviewing some of the basic elements that we use to describe our circuits.

Key Points

A capacitor consists of two plates separated by a dielectric

The charge stored on a capacitor is proportional to V

A capacitor blocks DC but appears to pass AC

The capacitance of several capacitors in parallel is equal to the sum of their individual capacitances

The capacitance of several capacitors in series is equal to the reciprocal of the sum of the reciprocals of the individual capacitances

In AC circuits current leads voltage by 90° in a capacitor

The energy stored in a capacitor is ½ $CV^2$ or ½ $Q^2 /C$
4.10 Why does a capacitor appear to pass AC signals while blocking DC signals?

4.11 How is the capacitance of a parallel-plate capacitor related to its dimensions?

4.12 The conducting plates of a capacitor are 5 × 15 mm and have a separation of $10 \; \mu m$. What would be the capacitance of such a device if the space between the plates were filled with air?

4.13 What would be the capacitance of the device described in Exercise 4.10 if the space between the plates were filled with a dielectric with a relative permittivity of $200$?

4.14 What is meant by stray capacitance, and why is this sometimes a problem?

⬇Download chapter 4 tutorial

Exercises

4.1 Explain what is meant by a dielectric.

4.2 If electrons represent negative charge in a capacitor, what constitutes positive charge?

4.3 If the two plates of a capacitor are insulated from each other, why does it appear that under some circumstances a current flows between them?

4.4 Why does the presence of charge on the plates of a capacitor represent the storage of energy?

4.5 How is the voltage across a capacitor related to the stored charge?

4.6 What are the units of measurement of capacitance?

4.7 A $100 \; \mu F$ capacitor has $5 V$ across its terminals. What quantity of charge is stored in it?

4.8 A $22 \; \mu F$ capacitor holds $1 \; mC$ of stored charge. What voltage is seen across its terminals?

4.9 A capacitor has a voltage of 25 $V$ across it when it holds $500 \; \mu C$ of charge. What is its capacitance?
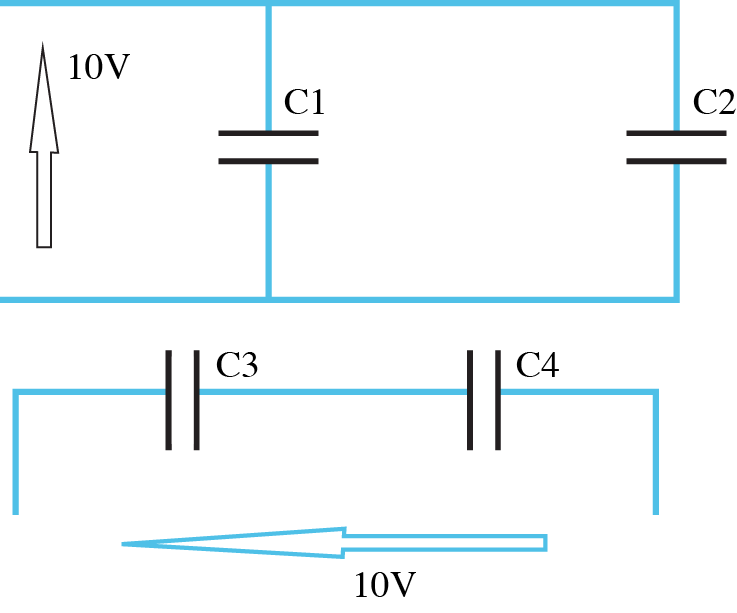
4.22 Determine the charge stored in the capacitors $C1, C2, C3$ and $C4$ in the arrangements shown in exercise 4.21.

4.23 How is voltage related to current in a capacitor?

4.24 Explain what is meant by a time constant. Given that $R = 50 \; k\Omega \text{ and } C = 10 \mu F$, what is the time constant of the following arrangement?

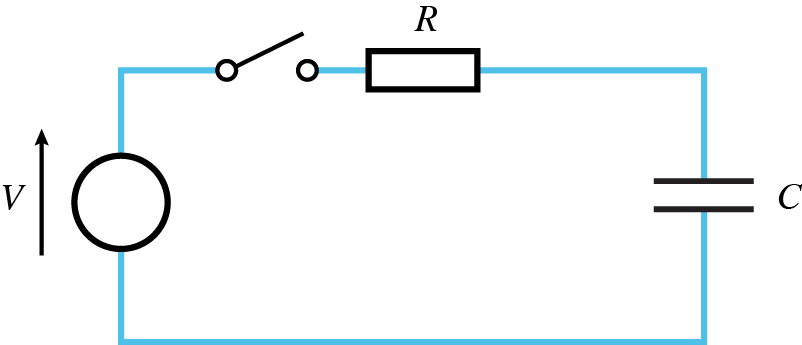
4.25 If the resistor in the circuit of Exercise 4.24 was increased by a factor of $10 \text{ to } 500 \; k\Omega$, what value of capacitor would be required to leave the time constant of the circuit unchanged?

4.26 Describe the relationship between the voltage across a capacitor and the current if the voltage is sinusoidal.

4.27 Give an expression for the energy stored in a charged capacitor.

4.28 A $5 \; mF$ capacitor is charged to $15 \; V$. What is the energy stored in the capacitor?

4.29 A $50 \; \mu F$ capacitor contains $1.25 \; mC$ of charge. What energy is stored in the capacitor?

⬇ Tutorial Solutions

Exercises (cont.)

4.15 Explain what is meant by an electric field and by electric field strength.

4.16 The plates of a capacitor have $250 \; V$ across them and have a separation of $15 \mu m$. What is the electric field strength in the dielectric?

4.17 What is meant by dielectric strength?

4.18 Explain what is meant by electric flux and by electric flux density.

4.19 The plates of a capacitor are 15 × 35 mm and store a charge of $35 \mu C$. Calculate the electric flux density in the dielectric.

4.20 Determine the effective capacitance of each of the following arrangements.

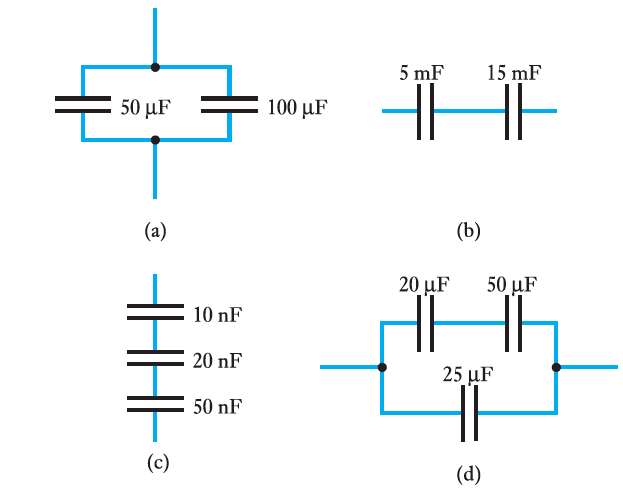
4.21 $\text{Given that } C_1 = 10 \; \mu F, C_2 = 20 \; \mu F, \\ C_3 = 10 \; \mu F \text{ and } C_4 = 20 \; \mu F$ determine the voltages across the capacitors in the following arrangements.