Week 6: Inductance and Magnetic Fields

Wk 6

Inductance and Magnetic Fields

Introduction

Electromagnetism

Reluctance

Inductance

Self-inductance

Inductors

Inductors in Series and in Parallel

Voltage and Current

Sinusoidal Voltages and Currents

Energy Storage in an Inductor

Mutual Inductance

Transformers

Circuit Symbols

The Use of Inductance in Sensors

Introduction

Earlier we noted that capacitors store energy by producing an electric field within a piece of dielectric material

Inductors also store energy, in this case it is stored within a magnetic field

In order to understand inductors, and related components such as transformers, we need first to look at electromagnetism
Example (cont.)

Adding a ferromagnetic ring around a wire will increase the flux by several orders of magnitude - since $\large \mu _r$ for ferromagnetic materials is 1000 or more

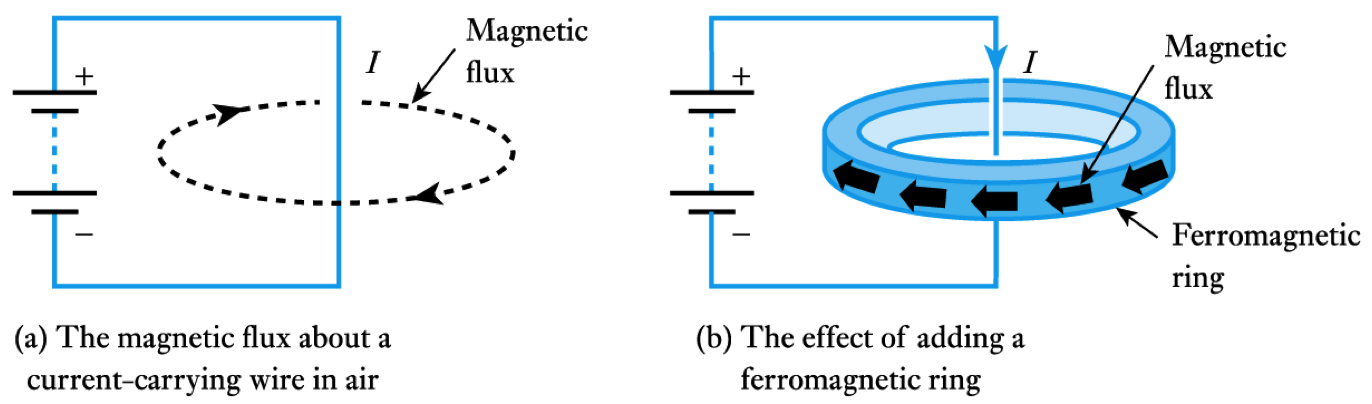
When a current-carrying wire is formed into a coil the magnetic field is concentrated

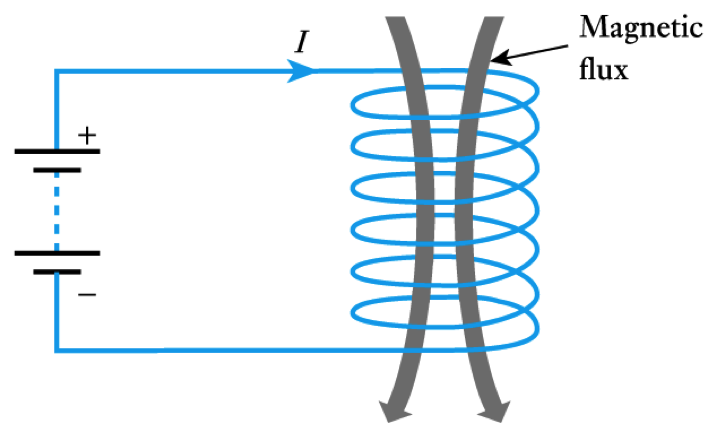
For a coil of $N$ turns the m.m.f. ($F$) is given by

\begin{align*} \large F = IN \end{align*}

and the field strength is

\begin{align*} \large F = \frac{IN}{l} \end{align*}

The magnetic flux produced is determined by the permeability of the material present

- a ferromagnetic material will increase the flux density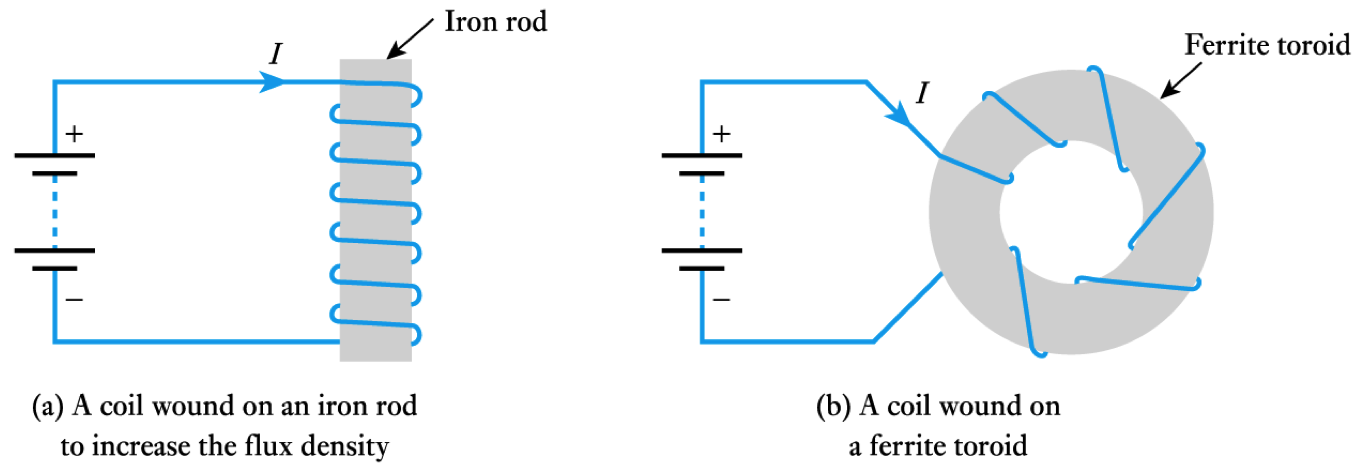

Electromagnetism

A wire carrying a current $I$ causes a magnetomotive force ($\; m.m.f \;$) $F$

– this produces a magnetic field

– F has units of Amperes

– for a single wire $F$ is equal to $I$

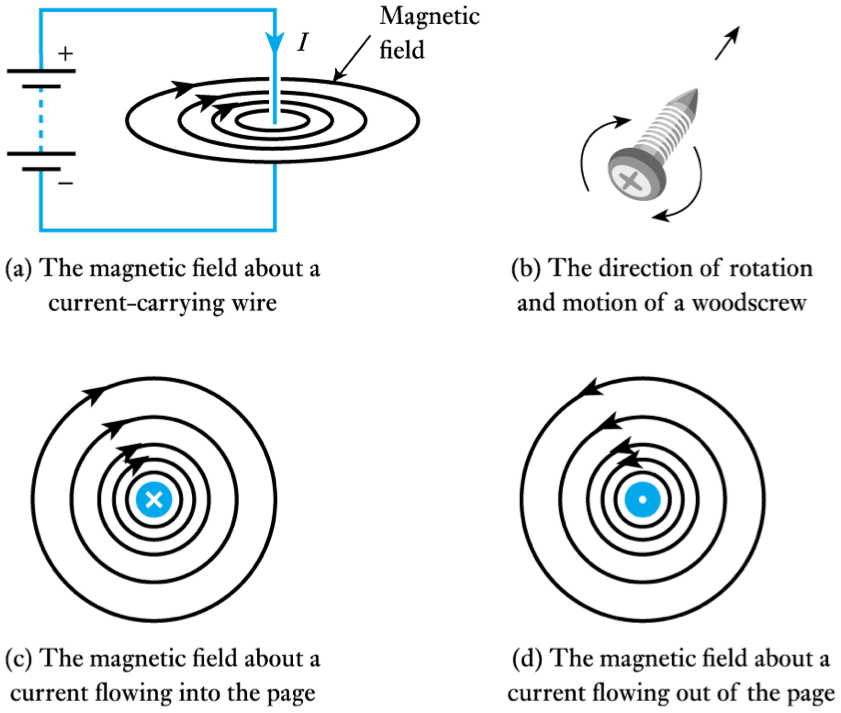
The magnitude of the field is defined by the magnetic field strength, $H$, where

\begin{align*} \large H = \frac{I}{l} \end{align*}

where l is the length of the magnetic circuit

Example – see Example 5.1 from course text A straight wire carries a current of $5 \; A$. What is the magnetic field strength $H$ at a distance of 100mm from the wire? Magnetic circuit is circular. $r = 100mm$, so path = $2\pi r = 0.628m$

\begin{align*} \large H &= \frac{\large I}{l} = \frac{\large 5}{0.628} = 7.96 \; \text{A/m} \end{align*}

The magnetic field produces a magnetic flux, $\phi$

- flux has units of weber (Wb)

Strength of the flux at a particular location is measured in term of the magnetic flux density, B

- flux density has units of tesla (T) (equivalent to 1 Wb/m2)

Flux density at a point is determined by the field strength and the material present

\begin{align*} \large B = \mu H \; \text{ or } \; B = \mu _0 \mu _r H \end{align*}
where $\large \mu _r$ is the permeability of the material, $ \large \mu _r$ is the relative permeability and $\large \mu_0$ is the permeability of free space
Inductors

The inductance of a coil depends on its dimensions and the materials around which it is formed

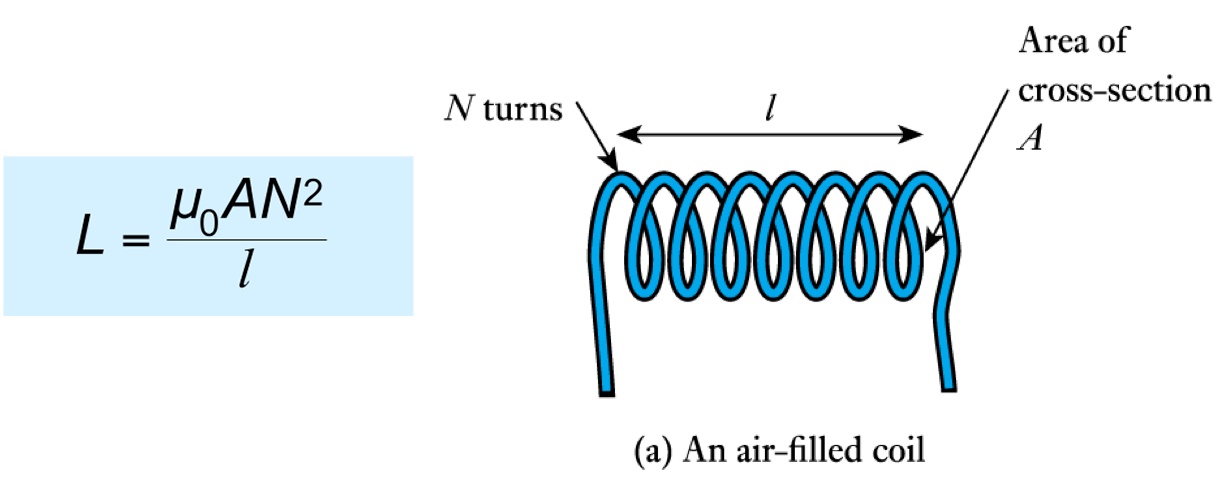
Click to see the equation above.

\begin{align*} \\ \\ \qquad \Large L = \frac{\mu _0 AN^2}{l} \qquad \\ \\ \end{align*}

The inductance is greatly increased through the use of a ferromagnetic core, for example

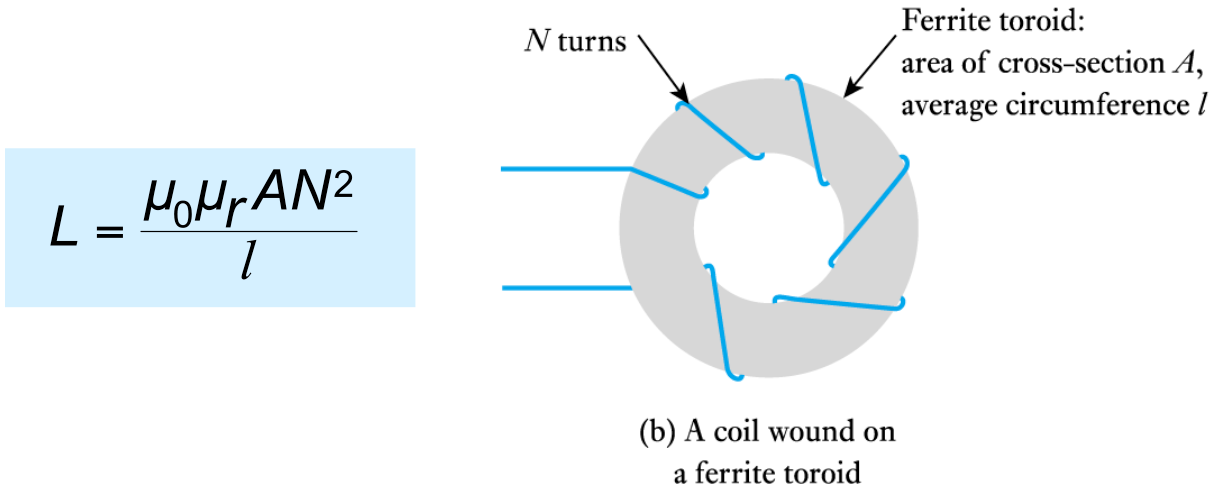
Click here to see the equation.

\begin{align*} \\ \\ \qquad \Large L = \frac{\mu _0 \mu _r AN^2}{l} \qquad \\ \\ \end{align*}

Equivalent circuit of an inductor

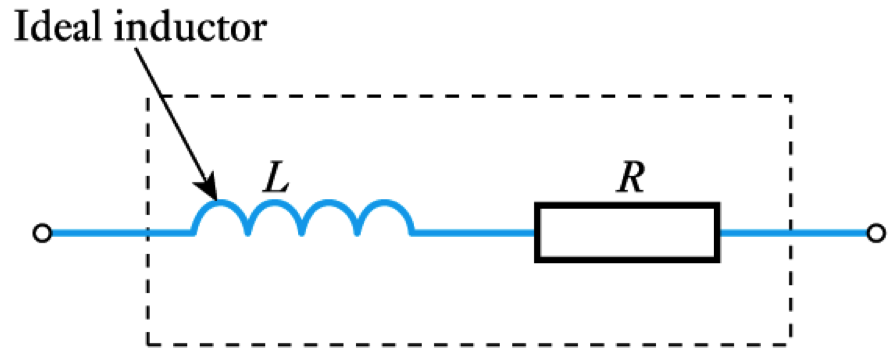
All real circuits also possess stray capacitance

Reluctance

In a resistive circuit, the resistance is a measure of how the circuit opposes the flow of electricity
In a magnetic circuit, the reluctance, $S$ is a measure of how the circuit opposes the flow of magnetic flux

In a resistive circuit $R = V/I$
In a magnetic circuit

\begin{align*} \large S = \frac{F}{\phi} \end{align*}

- the units of reluctance are amperes per weber (A/ Wb)

Inductance

A changing magnetic flux induces an e.m.f. in any conductor within it

Faraday’s law: The magnitude of the e.m.f. induced in a circuit is proportional to the rate of change of magnetic flux linking the circuit

Lenz’s law: The direction of the e.m.f. is such that it tends to produce a current that opposes the change of flux responsible for inducing the e.m.f.

When a circuit forms a single loop, the e.m.f. induced is given by the rate of change of the flux

When a circuit contains many loops the resulting e.m.f. is the sum of those produced by each loop

Therefore, if a coil contains $N$ loops, the induced voltage $V$ is given by

\begin{align*} \large V = N \frac{d \phi}{dt} \end{align*}

where $d \phi / dt$ is the rate of change of flux in Wb/s

This property, whereby an e.m.f. is induced as a result of changes in magnetic flux, is known as inductance

Self-inductance

A changing current in a wire causes a changing magnetic field about it

A changing magnetic field induces an e.m.f. in conductors within that field

Therefore when the current in a coil changes, it induces an e.m.f. in the coil

This process is known as self-inductance

\begin{align*} \large V = L \frac{d I}{dt} \end{align*}

where $L$ is the inductance of the coil (unit is the Henry)
Time constant

– we noted earlier that in a capacitor-resistor circuit the time required to charge to a particular voltage is determined by the time constant $CR$

– in this inductor-resistor circuit the time taken for the current to rise to a certain value is determined by L/R

– this value is again the time constant $\text{T}$ (greek tau)

See Computer Simulation Exercises 5.1 and 5.2 in the course text

Inductors in Series and Parallel

When several inductors are connected together their effective inductance can be calculated in the same way as for resistors – provided that they are not linked magnetically

Inductors in Series

Inductors in Parallel

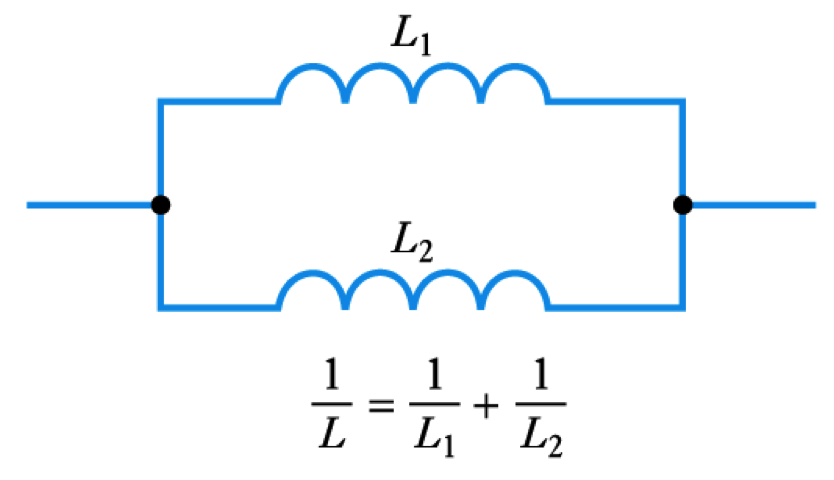
Voltage and Current

📷 Consider the circuit shown here

– inductor is initially un-energised

current through it will be zero

– switch is closed at $t = 0$

– $I$ is initially zero

hence $V _R$ is initially $0$

hence $V _L$ is initially $V$

– as the inductor is energised:

$I$ increases

$V _R$ increases

hence $V _L$ decreases

we have exponential behaviour
Energy Storage in an Inductor

Can be calculated in a similar manner to the energy stored in a capacitor

In a small amount of time dt the energy added to the magnetic field is the product of the instantaneous voltage, the instantaneous current and the time
\begin{align*} \text{Energy added } = vidt = L \frac {di}{dt} idt = Lidi \end{align*}

Thus, when the current is increased from zero to I

\begin{align*} \large E = L \int_{0}^{I} idt = \frac{1}{2} LI^2 \end{align*}

Sinusoidal Voltages and Currents

Consider the application of a sinusoidal current to an inductor

– from above $V = L \; dI/dt$

– voltage is directly proportional to the differential of the current

– the differential of a sine wave is a cosine wave

– the voltage is phase-shifted by 90° with respect to the current

– the phase-shift is in the opposite direction to that in a capacitor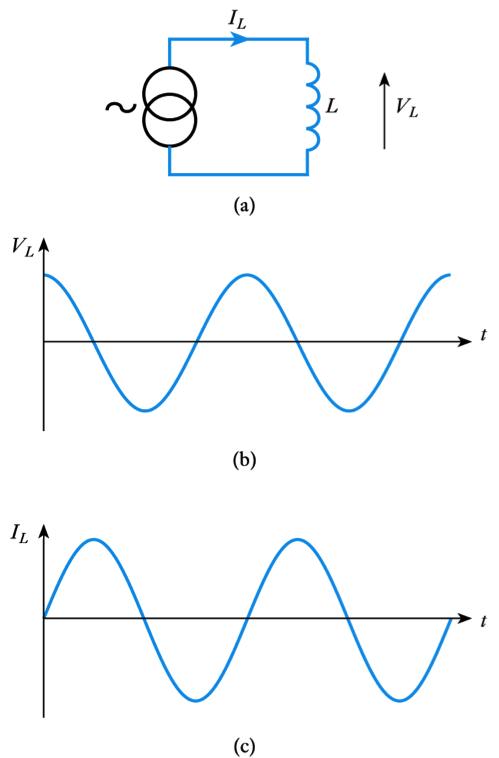
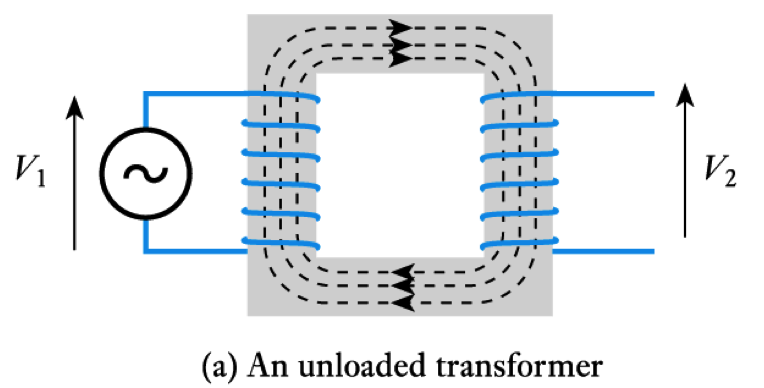
Transformers

🎥 Watch a video on transformers - Adobe Flash video

Most transformers approximate to ideal components
– that is, they have a coupling coefficient ≈ 1

– for such a device, when unloaded, their behaviour is determined by the turns ratio

– for alternating voltages

\begin{align*} \large \frac{V_2}{V_1} = \frac{N_2}{N_1} \end{align*}

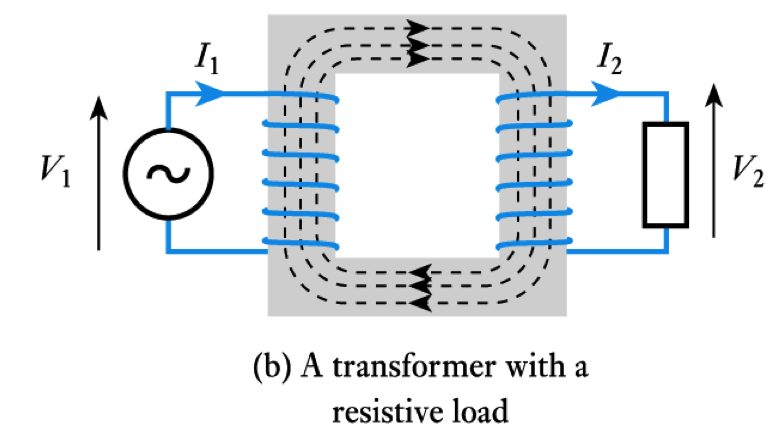
When used with a resistive load, current flows in the secondary
– this current itself produces a magnetic flux which opposes that produced by the primary

– thus, current in the secondary reduces the output voltage

– for an ideal transformer

\begin{align*} \large V_1 I_1 = V_2 I_2 \end{align*}

Mutual Inductance

When two coils are linked magnetically then a changing current in one will produce a changing magnetic field which will induce a voltage in the other

– this is mutual inductance

When a current I1 in one circuit, induces a voltage V2 in another circuit, then

\begin{align*} \large V_2 = M \frac{\;dI_1}{dt} \end{align*}

where $M$ is the mutual inductance between the circuits. The unit of mutual inductance is the Henry (as for self-inductance)

The coupling between the coils can be increased by wrapping the two coils around a core
– the fraction of the magnetic field that is coupled is referred to as the coupling coefficient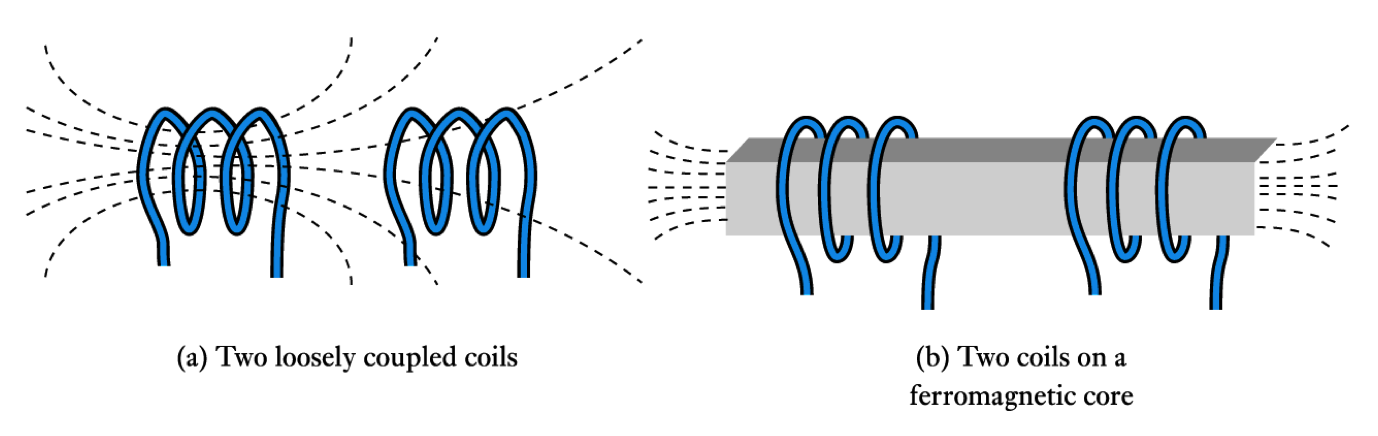

Coupling is particularly important in transformers
– the arrangements below give a coupling coefficient that is very close to $1$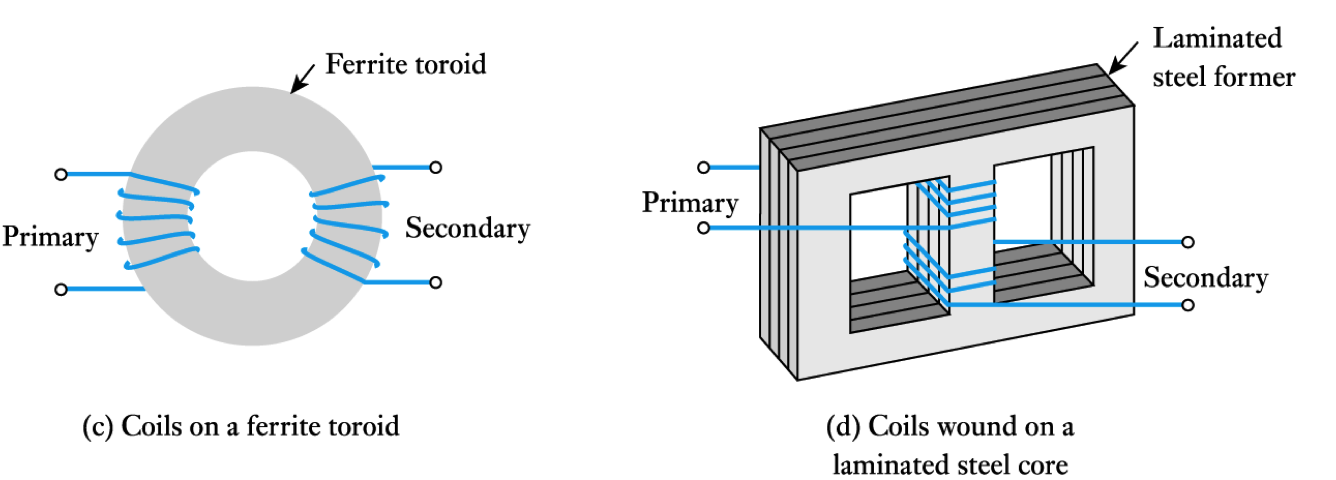
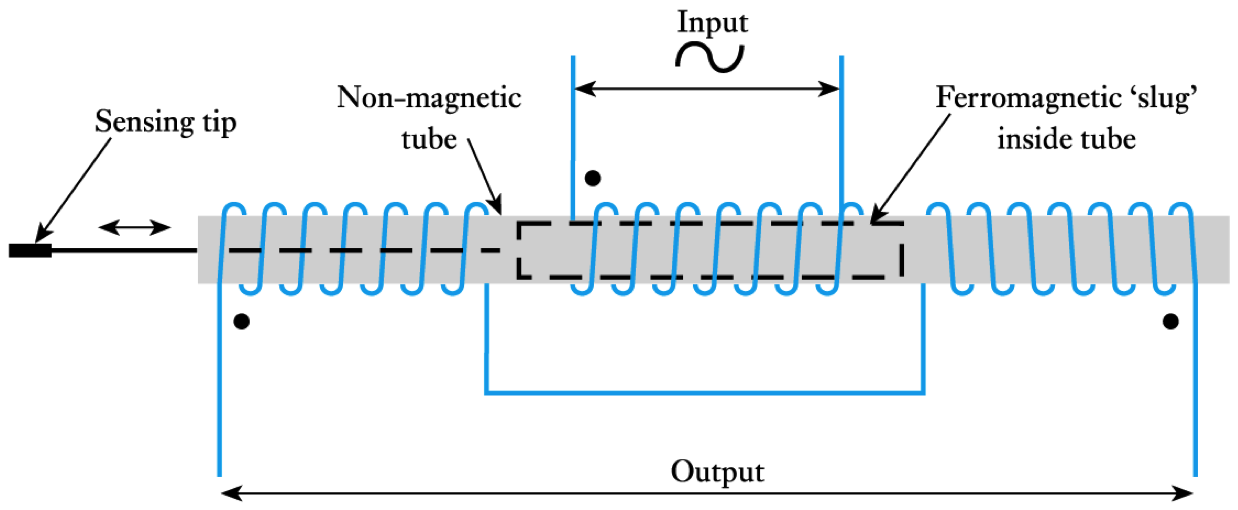
Linear variable differential transformers (LVDTs)
– see course text for details of operation of this device

The Use of Inductance in Sensors
🎥 Watch a video on the applications of inductive sensors - Adobe Flash video

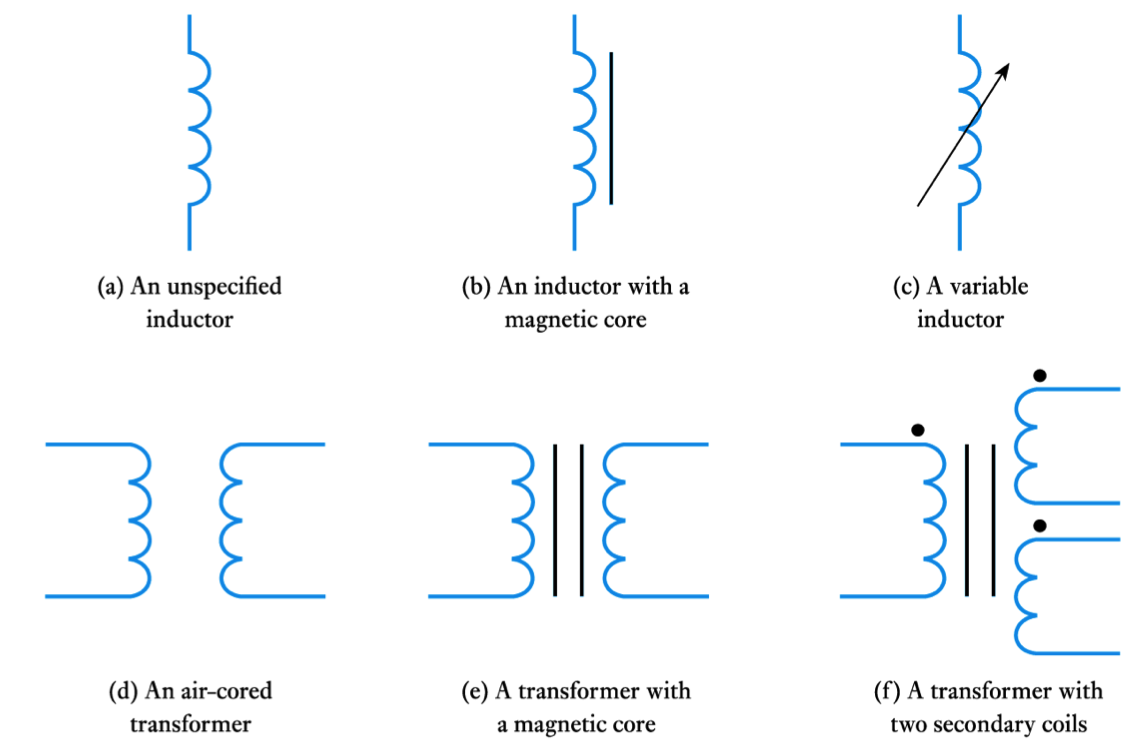
📷 Show circuit symbols

Numerous examples:

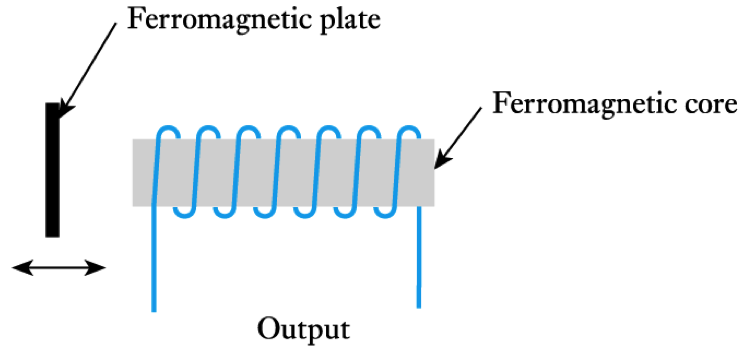
Inductive proximity sensors
– basically a coil wrapped around a ferromagnetic rod

– a ferromagnetic plate coming close to the coil changes its inductance allowing it to be sensed

– can be used as a linear sensor or as a binary switch
Key Points

Inductors store energy within a magnetic field

A wire carrying a current creates a magnetic field

A changing magnetic field induces an electrical voltage in any conductor within the field

The induced voltage is proportional to the rate of change of the current

Inductors can be made by coiling wire in air, but greater inductance is produced if ferromagnetic materials are used

The energy stored in an inductor is equal to ½ $LI^2$

When a transformer is used with alternating signals, the voltage gain is equal to the turns ratio
5.12 Explain what is meant by inductance.

5.13 Explain what is meant by self-inductance.

5.14 How is the voltage induced in a conductor related to the rate of change of the current within it?

5.15 Define the henry as it applies to the measurement of self-inductance.

5.16 The current in an inductor changes at a constant rate of $50 mA/s$, and there is a voltage across it of $150$ $\mu V$. What is its inductance?

5.17 Why does the presence of a ferromagnetic core increase the inductance of an inductor?

5.18 Calculate the inductance of a helical, air-filled coil $500 mm$ in length, with a cross-sectional area of $40 mm ^2$ and having $600$ turns.

5.19 Calculate the inductance of a coil wound on a ferromagnetic toroid of $300 mm$ mean circumference and $100 mm^2$ cross-sectional area, if there are $250$ turns on the coil and the relative permeability of the toroid is $800$.
5.20 How does a real inductor differ from an ideal component?

5.21 Why do all conductors introduce amounts of stray inductance into circuits?

⬇Download chapter 5 tutorial

Exercises

5.1 Explain what is meant by a magnetomotive force (m.m.f.).

5.2 Describe the field produced by a current flowing in a straight wire.

5.3 A straight wire carries a current of $3 A$. What is the magnetic field at a distance of 1 m from the wire? What is the direction of this field?

5.4 What factors determine the flux density at a particular point in space adjacent to a current-carrying wire?

5.5 Explain what is meant by the permeability of free space. What are its value and units?

5.6 Explain what is meant by relative permeability. What are its value and units? What would be typical values for this quantity for non-magnetic and ferromagnetic materials?

5.7 Give an expression for the magnetomotive force produced by a coil of $N$ turns that is passing a current of $I$ amperes.

5.8 A coil is formed by wrapping wire around a wooden toroid. The cross-sectional area of the coil is $400mm^2$, the number of turns is $600$, and the mean circumference of the toroid is $900mm$. If the current in the coil is $5A$, calculate the magnetomotive force, the magnetic field strength in the coil, the flux density in the coil and the total flux.

5.9 If the toroid in Exercise 5.8 were to be replaced by a ferromagnetic toroid with a relative permeability of $500$, what effect would this have on the values calculated?

5.10 If an m.m.f. of $15$ ampere-turns produces a total flux of 5 mWb, what is the reluctance of the magnetic circuit?

5.11 State Faraday’s law and Lenz’s law.
5.28 Discuss the implications of induced voltages when switching inductive circuits.

5.29 What is the relationship between the sinusoidal current in an inductor and the voltage across it?

5.30 What is the energy stored in an inductor of 2 mH when a current of 7 A is passing through it?

5.31 Explain what is meant by mutual inductance.

5.32 Define the henry as it applies to the measurement of mutual inductance.

5.33 What is meant by a coupling coefficient?

5.34 What is meant by the turns ratio of a transformer?

5.35 A transformer has a turns ratio of 10. A sinusoidal voltage of 5 V peak is applied to the primary coil, with the secondary coil open circuit. What voltage would you expect to appear across the secondary coil?

5.36 What would be the effect of adding a resistor across the secondary coil of the transformer in the arrangement described in Exercise 5.35?

5.37 What is meant by a step-up transformer?

5.38 What is meant by a step-down transformer?

5.39 Explain the dot notation used when representing transformers in circuit diagrams.

5.40 Describe the operation of an inductive proximity sensor.

5.41 Describe the construction and operation of an LVDT.

⬇ Tutorial Solutions

Exercises (cont.)

5.22 Calculate the effective inductance of the following arrangements.

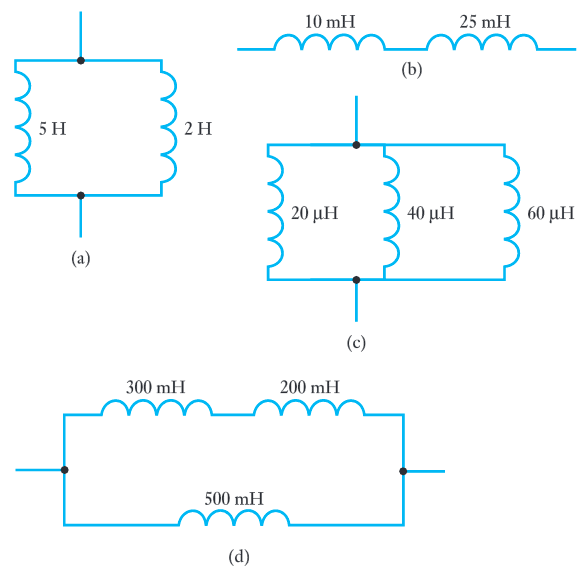
5.23 Describe the relationship between voltage and current in an inductor.

5.24 A constant current of 3 A is passed through a 12 H inductor. What voltage will be produced across the component?

5.25 Why is it not possible for the current in an inductor to change instantaneously?

5.26 Explain what is meant by a time constant. What is the time constant of a series LR circuit with R = 50Ω and L = 100 mH?

5.27 If the resistor in Exercise 5.26 is increased by a factor of 10, to 500Ω, what value of inductor would be required to leave the time constant of the circuit unchanged?