Wk 7

  • Alternating Voltages and Currents

    Introduction
    Reactance of Inductors and Capacitors
    Phasor Diagrams
    Impedance
    Complex Notation

    Introduction

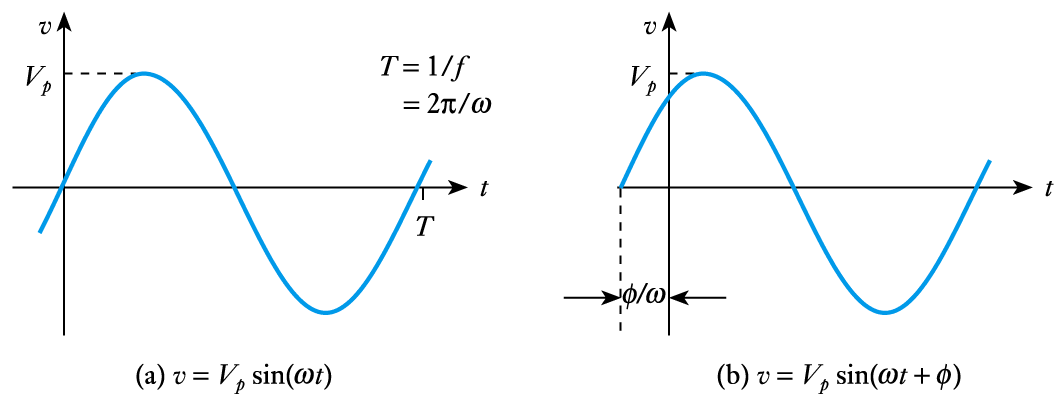
    From our earlier discussions we know that
    $\large V=V_p \; sin (\omega t + \phi)$
    where $V_p$ is the peak voltage
    $\omega$ is the angular frequency
    $\phi$ is the phase angle

    Since $\omega = 2 \pi f$ it follows that the period $T$ is given by
    \begin{align*} \large T = \frac{\large 1}{f} =\frac{\large 2 \pi}{\omega} \qquad \qquad \qquad \qquad \qquad \qquad \end{align*}

    📷   If $\phi$ is in radians, then a time delay t is given by $\phi / \omega$ (as shown here)

    Diagram

  • Inductance

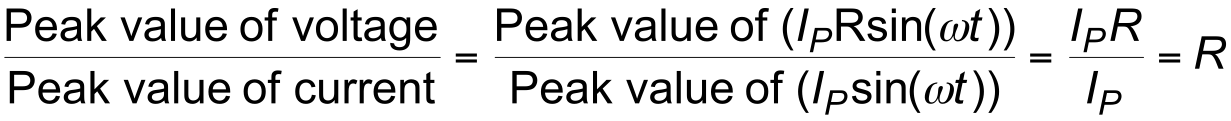
    Diagram

    Capacitance
    Diagram

    The ratio of voltage to current is a measure of how the component opposes the flow of electricity
    In a resistor this is termed its resistance
    In inductors and capacitors it is termed its reactance
    Reactance is given the symbol $X$
    Therefore
    \begin{align*} \text {Reactance of an inductor, }X_L = \omega L \end{align*}

    \begin{align*} \text {Reactance of an inductor, }X_C = \frac{1}{\omega C} \end{align*}

    Since reactance represents the ratio of voltage to current it has units of ohms
    The reactance of a component can be used in much the same way as resistance:

    – for an inductor$V = IX _L$
    – for a capacitor$V = IX _C$

    Example – see Example 6.3 from course text. A sinusoidal voltage of $5 V$ peak and $100\; Hz$ is applied across an inductor of $25 mH$. What will be the peak current?
    At this frequency, the reactance of the inductor is given by

    Diagram


    Therefore

    $$I_L = \frac{V_L}{X_L} = \frac{5}{15.7} = 318 \; mA \text{ peak}$$

    Voltage and Current

    🎥  Watch a video on alternating voltages and currents - Adobe Flash video
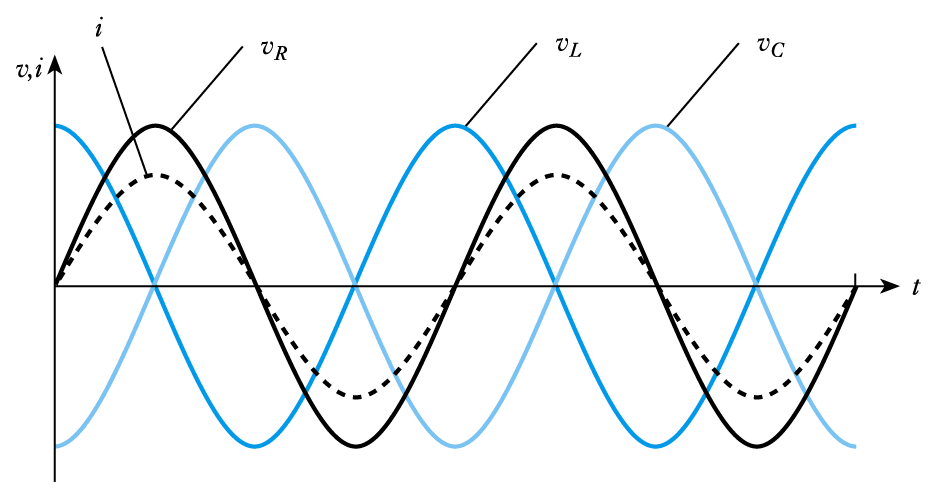
    Consider the voltages across a resistor, an inductor and a capacitor, with a current of
    \begin{align*} \large i = I_p\; sin (\omega t) \qquad \qquad \qquad \qquad \qquad \qquad \end{align*}
    Resistors
    – from Ohm law we know $$V_R = iR$$ – therefore if $i =I_P \; \text{sin} (\omega t)$
    $$ V_R = I_PR \; \text{sin} (\omega t) $$

    Inductors - in an inductor
    $$V_L = L \frac{di}{dt}$$
    – therefore if $i=I_P\; sin(\omega t)$

    $$ V_L = L\frac{d(I_P \; sin (\omega t))}{dt} = \omega LI _P \; cos (\omega t) $$

    Capacitors - in a capacitor
    $$ V_C = \frac{1}{C} \int idt $$
    – therefore if $i = I _P\; sin (\omega t)$
    $$V _C = \frac{1}{C} \int I _P \; sin (\omega t) = - \frac{I _P}{\omega C} \; cos (\omega t)$$

    📷   See this diagram

    Reactance of Inductors and Capacitors

    Let us ignore, for the moment the phase angle and consider the magnitudes of the voltages and currents
    Let us compare the peak voltage and peak current
    Resistance

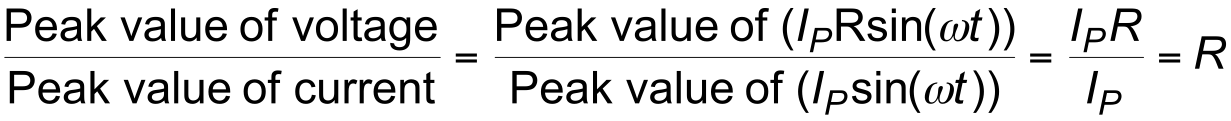
    Diagram


    Diagram
  • 📷   Phasor diagrams can be used to represent the addition of signals. This gives both the magnitude and phase of the resultant signal (can be seen here)

    📷   Phasor diagrams can also be used to show the subtraction of signals

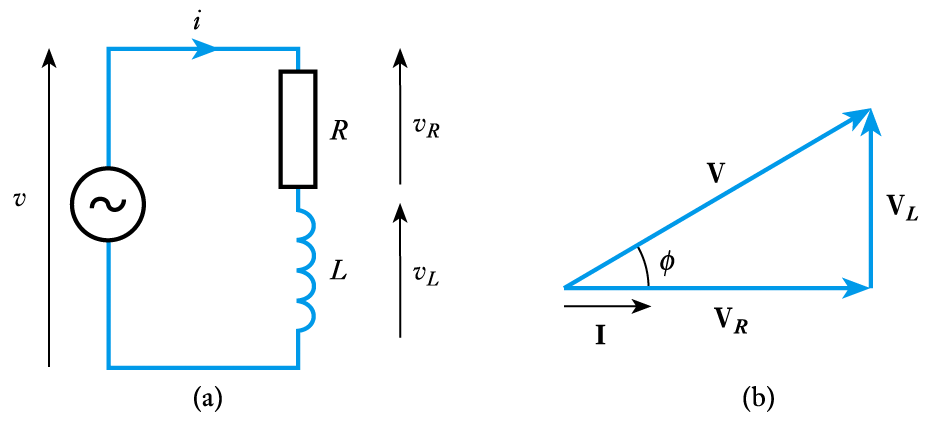
    📷   Phasor analysis of an $RL$ circuit
    See Example 6.5 in the text for a numerical example

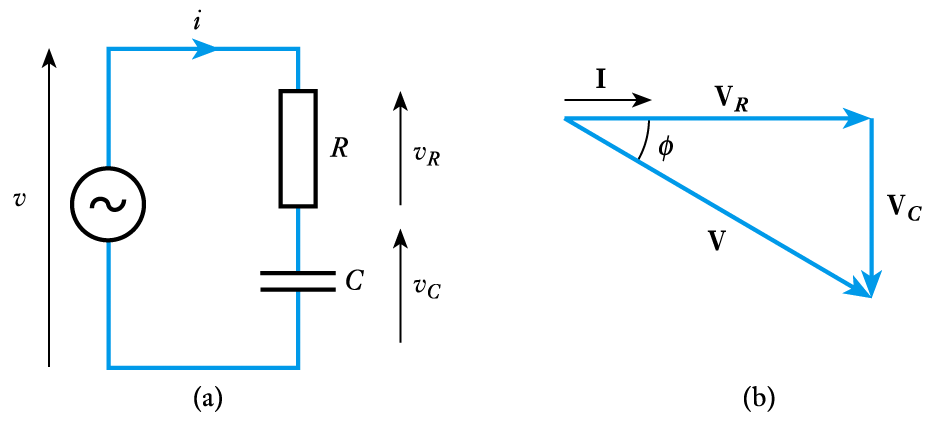
    📷   Phasor analysis of an $RC$ circuit
    See Example 6.6 in the text for a numerical example

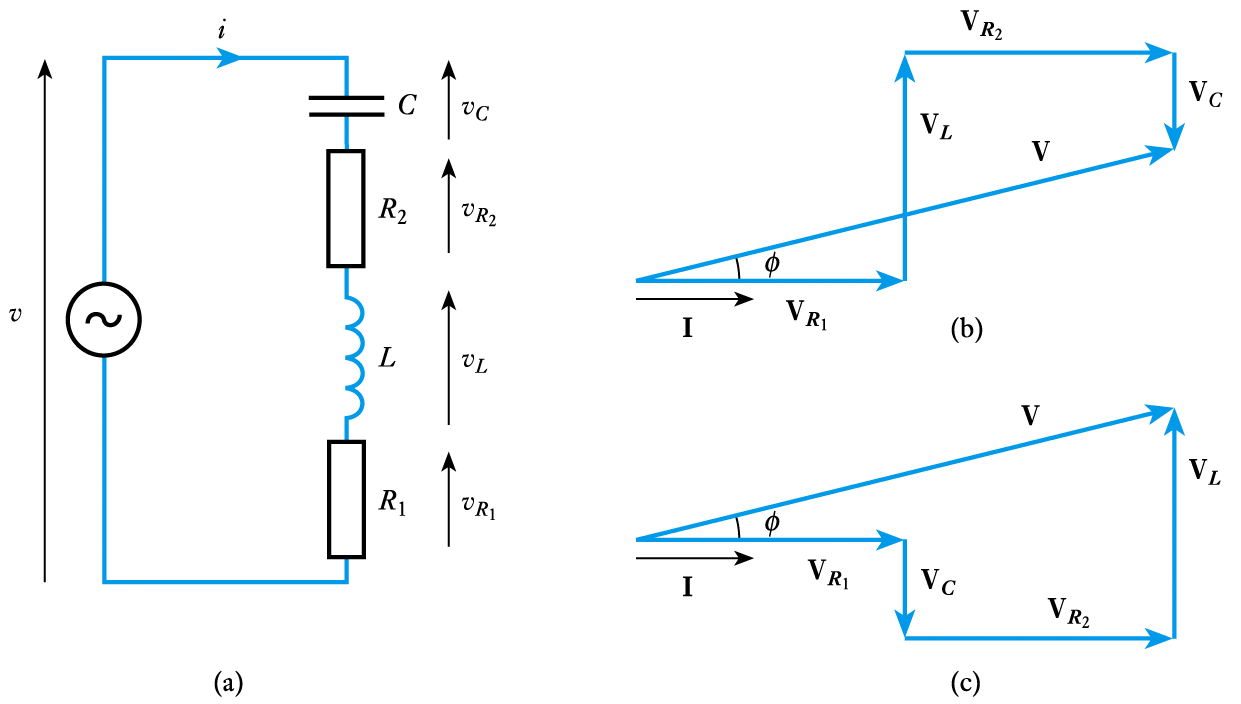
    📷   Phasor analysis of an $RLC$ circuit

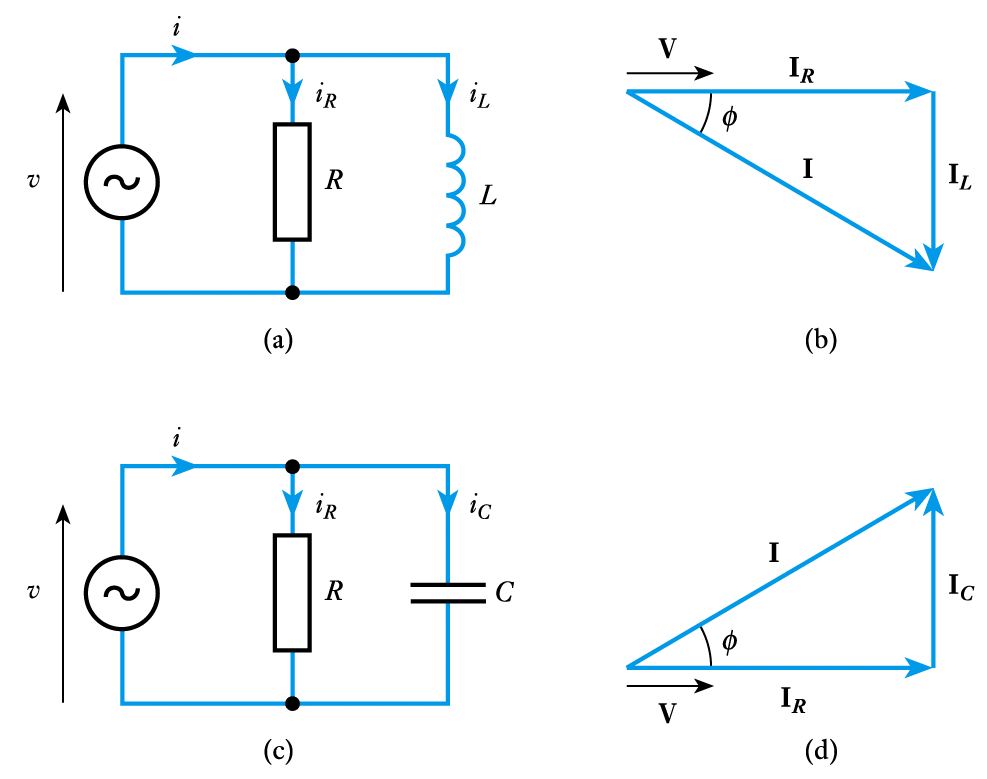
    Phasor analysis of parallel circuits
    in such circuits the voltage across each of the components is the same and it is the currents that are of interest
    Diagram

    Phasor Diagrams

    Sinusoidal signals are characterised by their magnitude, their frequency and their phase
    In many circuits the frequency is fixed (perhaps at the frequency of the AC supply) and we are interested in only magnitude and phase
    In such cases we often use phasor diagrams which represent magnitude and phase within a single diagram

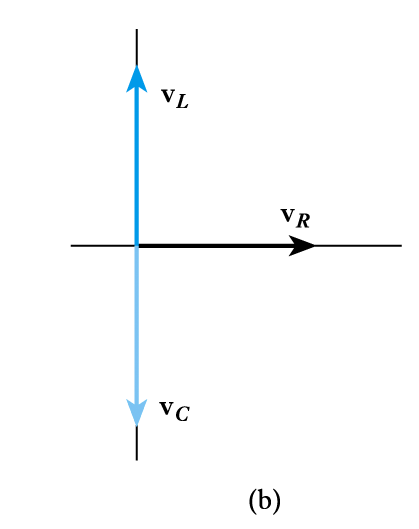
    Examples of phasor diagrams (a) here $L$ represents the magnitude and $ \large \phi$ the phase of a sinusoidal signal
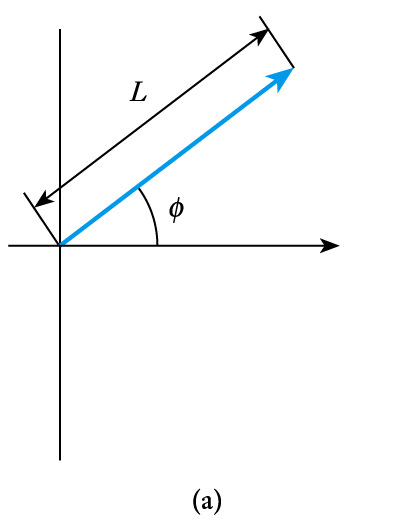
    Diagram

    (b) shows the voltages across a resistor, an inductor and a capacitor for the same sinusoidal current
    Diagram

    Diagram
    Diagram
    Diagram
    Diagram
    Diagram

  • From the phasor diagram the phase angle of the impedance is given by
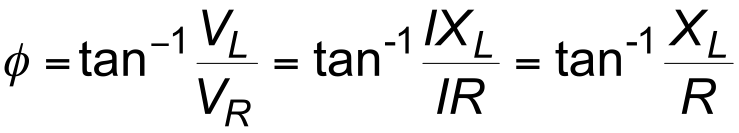    Diagram

    This circuit contains an inductor but a similar analysis can be done for circuits containing capacitors

    In general
    \begin{align*} Z = \sqrt{R^2 = X^2} \end{align*}
    $$\text{And}$$
    \begin{align*} \phi = \text{tan} ^{-1} \frac{X}{R} \end{align*}

    A graphical representation of impedance
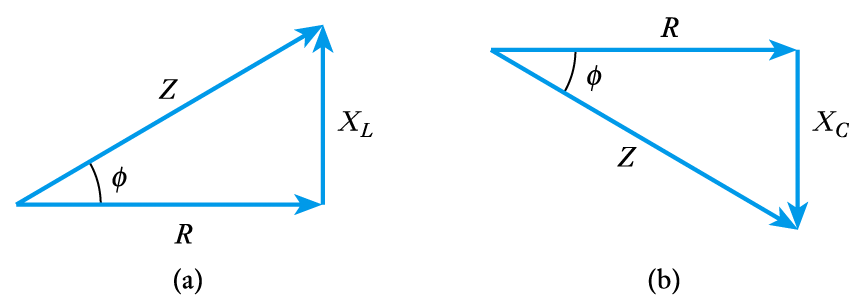
    Diagram

    Diagram

    Impedance

    In circuits containing only resistive elements the current is related to the applied voltage by the resistance of the arrangement
    In circuits containing reactive, as well as resistive elements, the current is related to the applied voltage by the impedance, $Z$ of the arrangement
    – this reflects not only the magnitude of the current but also its phase
    – impedance can be used in reactive circuits in a similar manner to the way resistance is used in resistive circuits

    Consider the following circuit and its phasor diagram
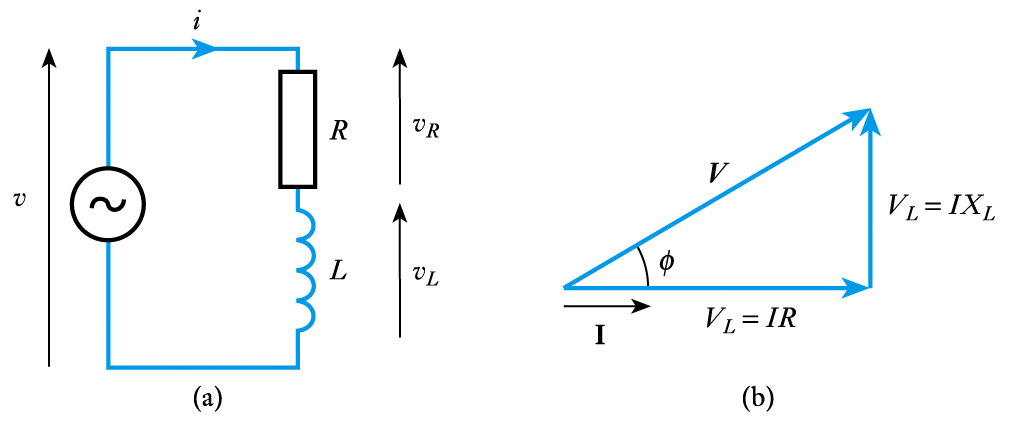
    Diagram

    From the phasor diagram it is clear that that the magnitude of the voltage across the arrangement $V$ is
    \begin{align*} V =& \sqrt{V_R \; ^2 + V_L \; ^2} \\ =& \sqrt{(I R)^2 + (I X_L)^2} \\ =& I \sqrt{R^2 + X_L \; ^2} \\ =& I Z \\ \text{ Where} \\ Z =& \sqrt{R^2 + X_L \;^2} \end{align*}

    $Z$ is the magnitude of the impedance, so    $Z =$|$Z$|

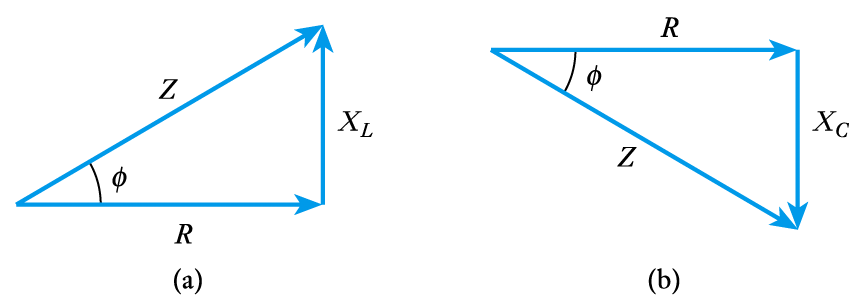
    Diagram
    Diagram
  • Manipulating complex impedances
    – complex impedances can be added, subtracted, multiplied and divided in the same way as other complex quantities
    – they can also be expressed in a range of forms such as the rectangular, polar and exponential forms
    – if you are unfamiliar with the manipulation of complex quantities (or would like a little revision on this topic) see Appendix D of the course text which gives a tutorial on this subject

    Example – see Example 6.7 in the course text.
    Determine the complex impedance of this circuit at a frequency of $50\; Hz$
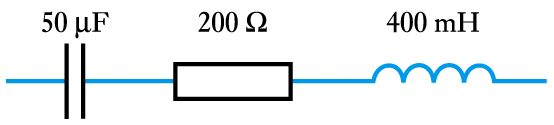
    Diagram

    At 50Hz, the angular frequency $\omega = 2 \pi f = 2 \times \pi \times 50 =314 \text{ rad/s}$

    Therefore

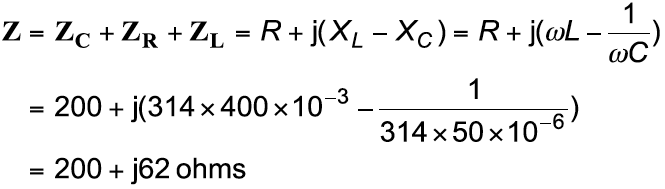
    Diagram

    Using complex impedance
    Diagram

    (Example continued on next screen).

    Complex Notation

    Phasor diagrams are similar to Argand Diagrams used in complex mathematics

    We can also represent impedance using complex notation where

    Resistors: $Z_R = R$

    Inductors: $Z_L = jX_L = j \omega L$

    Capacitors: $ Z_c = -jX_C = -j\frac{1}{\omega C} = \frac{1}{j \omega C}$

    Graphical representation of complex impedance Diagram

    Series and parallel combinations of impedances
    – impedances combine in the same way as resistors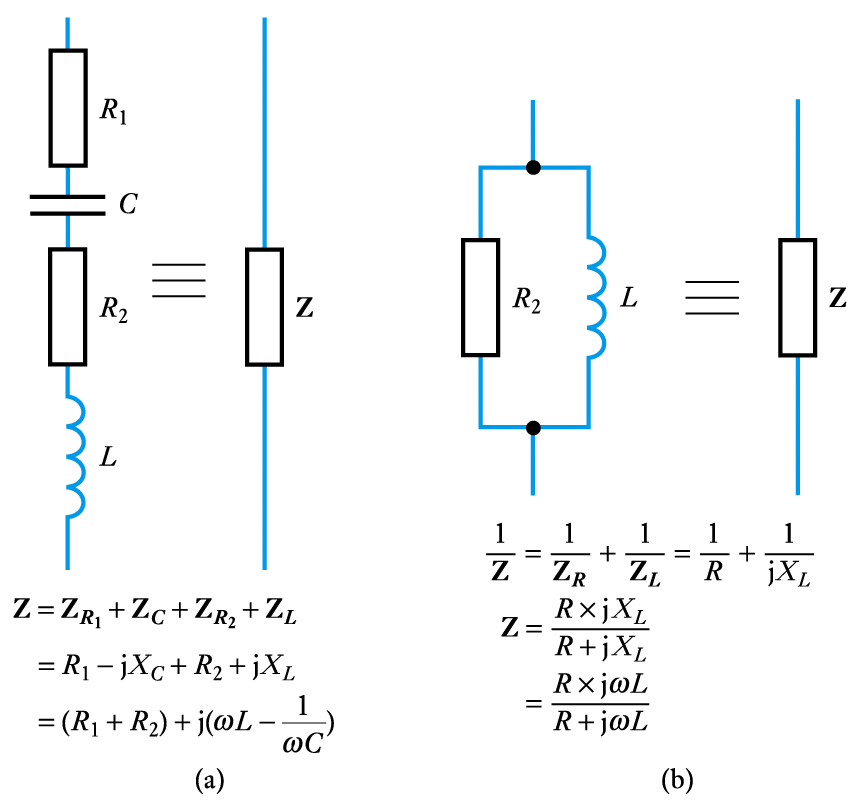
    Diagram

    Diagram
    Diagram

  • A further example
    A more complex task is to find the output voltage of this circuit The analysis of this circuit, and a numerical example based on it, are given in Section 6.6.4 and Example 6.8 of the course text.
    Diagram

    (Cont.)

    Example – see Section 6.6.4 in course text Determine the current in this circuit Since $v = 100 \text{ sin } 250 t$ , then $\omega = 250$

    Therefore

    \begin{align*} Z =& R - jX_C \\ =& R - j \frac{1}{\omega C} \\ =& 100 - j \frac{1}{250 \times 10 ^{-4}} \\ =& 100 - j 40 \end{align*}

    The current is given by $v$/$Z$ and this is easier to compute in polar form

    \begin{align*} Z =& 100 - j40 \\ |Z| =& \sqrt{100^2 + 40^2} - 107.7 \\ \angle{Z}=& \text{ tan} ^{\large -1} \frac{ - 40}{100} = -21.8 ^\circ \\ Z=& 107.7 \angle{} - 21.8^\circ \end{align*}

    Therefore
    \begin{align*} i = \frac{v}{Z} = \frac{100 \angle{0} }{107.7 \angle{} - 21.8} = 0.93 \angle{21.8^\circ} \end{align*}


  • Further Study

    🎥  Watch a video on using complex impedance - Adobe Flash video
    The Further Study section at the end of Chapter 6 looks at the characteristics of a simple reactive circuit.
    See if you can model the behaviour of the circuit at a single frequency and then watch the video to check your analysis.

    Key Points

    A sinusoidal voltage waveform can be described by the equation $ v = V _P \text{ sin } (\omega t + \phi)$
    The voltage across a resistor is in phase with the current, the voltage across an inductor leads the current by 90°, and the voltage across a capacitor lags the current by 90°
    The reactance of an inductor $X_L = \omega L$
    The reactance of a capacitor $X_C = 1/ \omega C$
    The relationship between current and voltage in circuits containing reactance can be described by its impedance
    The use of impedance is simplified by the use of complex notation
  • 6.10 If a sinusoidal current is passed through a resistor, what is the phase relationship between this current and the voltage across the component?
    6.11 If a sinusoidal current is passed through a capacitor, what is the phase relationship between this current and the voltage across the component?
    6.12 If a sinusoidal current is passed through an inductor, what is the phase relationship between this current and the voltage across the component?
    6.13 How can the word ‘civil’ assist in remembering the phase relationship between currents and voltages in inductors and capacitors?
    6.14 Explain what is meant by the term ‘reactance’.
    6.15 What is the reactance of a resistor?
    6.16 What is the reactance of an inductor?
    6.17 What is the reactance of a capacitor?
    6.18 Calculate the reactance of an inductor of 20 $mH$ at a frequency of $100 \; Hz$, being sure to include the units in your answer.
    6.19 Calculate the reactance of a capacitor of 10 $nF$ at an angular frequency of 500 rad /s, being sure to include the units in your answer.
    6.20 A sinusoidal voltage of 15 $V$ r.m.s. at $250\; Hz$ is applied across a 50 $\mu F$ capacitor. What will be the current in the capacitor?
    6.21 A sinusoidal current of 2 $mA$ peak at 100 rad/s flows through an inductor of 25 $mH$. What voltage will appear across the inductor?
    6.22 Explain briefly the use of a phasor diagram.
    6.23 What is the significance of the length and direction of a phasor?
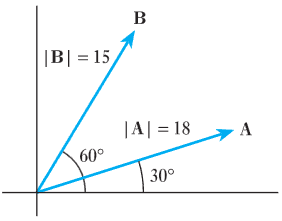
    6.24 Estimate the magnitude and phase of ( $A + B$ ) and ( $A − B$ ) in the following phasor diagram.
    Diagram

    ⬇Download chapter 6 tutorial

    Exercises

    6.1 A signal v is described by the expression $v = 15 \text{ sin } 100t$. What is the angular frequency of this signal, and what is its peak magnitude?
    6.2 A signal v is described by the expression $v = 25 \text{ sin } 250 t$ . What is the frequency of this signal (in Hz), and what is its r.m.s. magnitude?
    6.3 Give an expression for a sinusoidal signal with a peak voltage of $20 \; V$ and an angular frequency of $300$ rad/s.
    6.4 Give an expression for a sinusoidal signal with an r.m.s. voltage of $14.14 V$ and a frequency of $50\; Hz$.
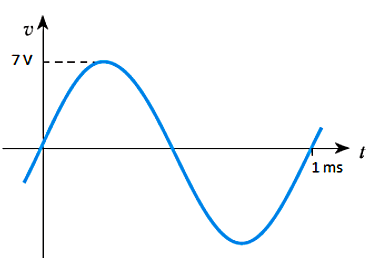
    6.5 Give an expression for the waveform shown in the following diagram.
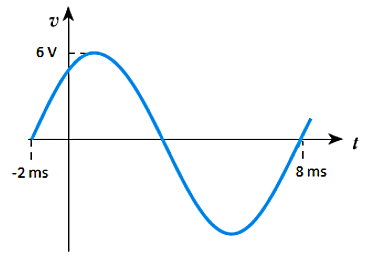
    Diagram

    6.6 Give an expression for the waveform shown in the following diagram.
    Diagram

    6.7 Give an expression relating the voltage across a resistor to the current through it.
    6.8 Give an expression relating the voltage across an inductor to the current through it.
    6.9 Give an expression relating the voltage across a capacitor to the current through it.
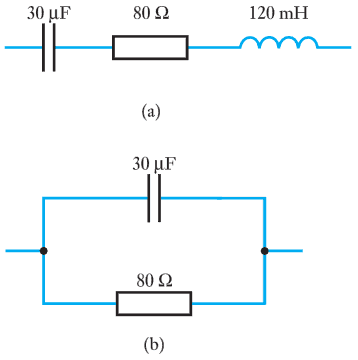
  • 6.34 Determine the complex impedance of the following arrangements at a frequency of $100\; Hz$.
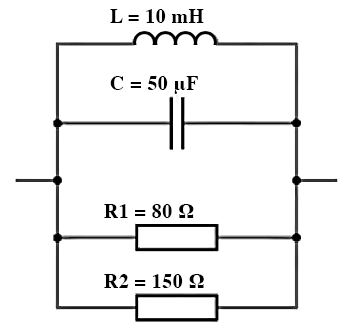
    Diagram

    6.35 Use your answer to Exercise 6.34 to devise a simpler arrangement of components that would have a similar behaviour to the circuit of Exercise 6.34 at a frequency of $100\; Hz$.
    6.36 Repeat the calculations of Exercise 6.34 assuming that the circuit will be used at a frequency of $200\; Hz$.
    6.37 Use your answer to Exercise 6.36 to devise a simple arrangement of components that would have a similar behaviour to the circuit of Exercise 6.34 at a frequency of $200\; Hz$.
    6.38 Express $x = 20 + j30$ in polar form and in exponential form.
    6.39 Express $y = 25 \angle{} − 40^\circ$ in rectangular form and in exponential form.
    6.40 A voltage $v = 60 \text{ sin } 314 t$ is applied across a series combination of a $10 \Omega$ resistor and an inductance of $50 mH$. Determine the magnitude and phase of the resulting current.
    6.41 A current of $i = 0.5 \text{ sin } 377 t$ is passed through a parallel combination of a resistance of $1 k \Omega$ and a capacitance of $5 \mu F$. Determine the magnitude and phase of the resulting voltage across the combination.

    ⬇ Tutorial Solutions

    Exercises (cont.)

    6.25 A voltage is formed by summing two sinusoidal waveforms of the same frequency. The first has a magnitude of $20 V$ and is taken as the reference phase (that is, its phase angle is taken as 0°). The second has a magnitude of $10 V$ and leads the first waveform by 45°. Draw a phasor diagram of this arrangement and hence estimate the magnitude and phase of the resultant signal.
    6.26 A sinusoidal current of 3 A at $100\; Hz$ flows through a series combination of a resistor of 25 $\Omega$ and an inductor of $75 mH$. Use a phasor diagram to determine the voltage across the combination and the phase angle between this voltage and the current.
    6.27 A sinusoidal voltage of $12 V$ at $500\; Hz$ is applied across a series combination of a resistor of $5 k \; \Omega$ and a capacitor of $100 nF$. Use a phasor diagram to deter- mine the current through the combination and the phase angle between this current and the applied voltage.
    6.28 Use a phasor diagram to determine the magnitude and phase angle of the impedance formed by the series combination of a resistance of 25 $\Omega$ and a capacitance of $10 \mu F$, at a frequency of $300\; Hz$.
    6.29 If $x = 5 + j7$ and $y = 8 − j10$, evaluate $( x + y ), ( x − y ), ( x \times y )$ and $( x \div y )$.
    6.30 What is the complex impedance of a resistor of $1 k \Omega$ at a frequency of $1 \; kHz$?
    6.31 What is the complex impedance of a capacitor of $1 \mu F$ at a frequency of $1 \; kHz$?
    6.32 What is the complex impedance of an inductor of $1 mH$ at a frequency of $1 \; kHz$?
    6.33 Determine the complex impedance of the following arrangements at a frequency of $200\; Hz$.
    Diagram