Wk 8

  • Power in AC Circuits

    Introduction
    Power in Resistive Components
    Power in Capacitors
    Power in Inductors
    Circuits with Resistance and Reactance
    Active and Reactive Power
    Power Factor Correction
    Three-Phase Systems
    Power Measurement

    Introduction

    The instantaneous power dissipated in a component is a product of the instantaneous voltage and the instantaneous current $p = vi$
    In a resistive circuit the voltage and current are in phase – calculation of $p$ is straightforward
    In reactive circuits, there will normally be some phase shift between $v$ and $i$, and calculating the power becomes more complicated

  • Power in Capacitors

    From our discussion of capacitors we know that the current leads the voltage by $90 ^\circ$. Therefore, if a voltage $v = V_P \text{ sin } Ο‰t$ is applied across a capacitance $C$, the current will be given by $i$ = $I _p \text{ cos } Ο‰t$

    Then \begin{align*} p &= vi \\ &= V_P \text{ sin } \omega t \times I_P \text{ cos } \omega t\\ &= V_P I_P (\text{sin } \omega t \times \text{cos } \omega t) \\ &= V_P I_P (\frac{\text{sin }2 \omega t}{2}) \\ \end{align*}
    The average power is zero

    πŸ“·   Relationship between $v$, $i$ and $p$ in a capacitor

    Power in Resistive Components

    Suppose a voltage $v=V_P \text{ sin } \omega t$ is applied across a resistance $R$. The resultant current $i$ will be
    $$ i = \frac{v}{R} = \frac{V_P \text{ sin }\omega t}{R} = I_P \text{ sin } \omega t $$
    The result power $p$ will be
    \begin{align*} p &= vi \\ &= V_P \text{ sin }\omega t \times I _P \text{ sin } \omega t \\ &= V_P I_P ( \text{sin}^2 \; \omega t) \\ &= V_P I_P (\frac{1 - \text{cos } 2 \omega t}{2}) \end{align*}
    The average value of $(1 - \text{cos } 2Ο‰t) \text{ is } 1$,so
    Average Power \begin{align*} &= \frac{1}{2} V_PI_P \\ &= \frac{V_P}{ \sqrt{2}} \times \frac{I_P}{ \sqrt{2}} \\ &= VI \\ \end{align*}
    where $V$ and $I$ are the r.m.s. voltage and current

    πŸ“·   Relationship between $v$, $i$ and $p$ in a resistor (can be seen here)



    Diagram
    Diagram

  • (Continued)

    The first part represents the power dissipated in resistive components. Average power dissipation is

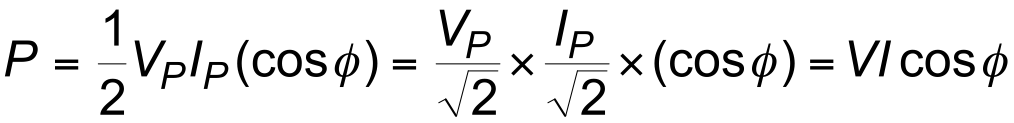
    Diagram
    The average power dissipation given by
    $$ p = \frac{1}{2} V_P I_P \; (\text{cos}\phi) = VI \text{cos} \phi $$ is termed the active power in the circuit and is measured in watts ($W$)

    The product of the r.m.s. voltage and current VI is termed the apparent power, $S$. To avoid confusion this is given the units of volt amperes ($VA$)

    From the above discussion it is clear that
    \begin{align*} p &= VI \; \text{cos} \phi \\ &= S \text{ cos} \phi \end{align*}
    In other words, the active power is the apparent power times the cosine of the phase angle.
    This cosine is referred to as the power factor

    Diagram

    Power in Inductors

    From our discussion of inductors we know that the current lags the voltage by $90 ^\circ$. Therefore, if a voltage $v=V_P \text{ sin } Ο‰t$ is applied across an inductance $L$, the current will be given by $i = -I_P \text{ cos } Ο‰t$

    Therefore \begin{align*} p &= vi \\ &= V_P \text{ sin } \omega t \times I_P \text{ cos } \omega t\\ &= V_P I_P (\text{sin } \omega t \times \text{cos } \omega t) \\ &= V_P I_P (\frac{\text{sin }2 \omega t}{2}) \\ \end{align*}
    Again the average power is zero

    πŸ“·   Relationship between $v$, $i$ and $p$ in an inductor

    Circuit with Resistance and Reactance

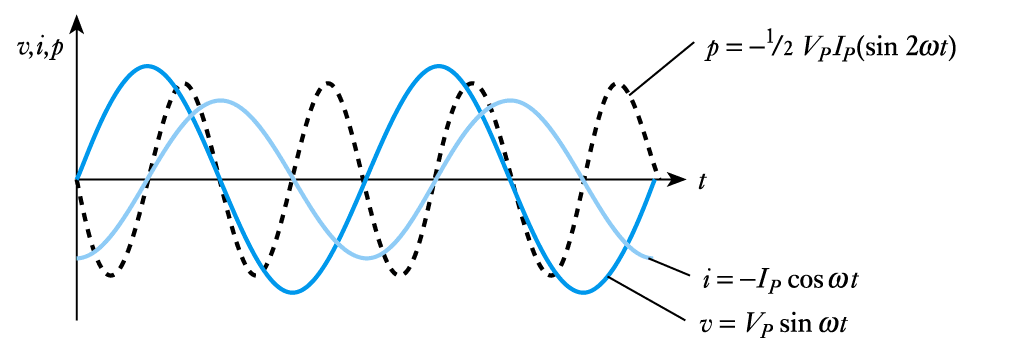
    When a sinusoidal voltage $v = V_P \text{ sin } Ο‰t $ is applied across a circuit with resistance and reactance, the current will be of the general form $i = I_P \text{ sin } (Ο‰t - \phi )$
    Therefore, the instantaneous power, $p$ is given by
    \begin{align*} p &= vi \\ &= V_P \text{ sin } \omega t \times I_P \text{ sin } (\omega t - \phi)\\ &= \frac{1}{2} V_P I_P \; \text{cos } \phi - \text{ cos }(2 \omega t - \phi)\\ p &= \frac{1}{2} V_P I_P \; \text{cos } \phi - \frac{1}{2} V_P I_P \; \text{cos } (2 \omega t -\phi) \\ p &= \frac{1}{2} V_P I_P \; \text{cos } \phi - \frac{1}{2} V_P I_P \; \text{cos } (2 \omega t -\phi) \end{align*}
    The expression for $p$ has two components
    The second part oscillates at $2 \omega$ and has an average value of zero over a complete cycle
    – this is the power that is stored in the reactive elements and then returned to the circuit within each cycle


    Diagram

  • Power Factor Correction

    Power factor is particularly important in high-power applications
    Inductive loads have a lagging power factor
    Capacitive loads have a leading power factor power factor
    Many high-power devices are inductive
    – a typical AC motor has a power factor of $0.9$ lagging
    – the total load on the national grid is $0.8-0.9$ lagging
    – this leads to major efficiencies
    – power companies therefore penalise industrial users who introduce a poor power factor

    The problem of poor power factor is tackled by adding additional components to bring the power factor back closer to unity
    – a capacitor of an appropriate size in parallel with a lagging load can β€˜cancel out’ the inductive element
    – this is power factor correction
    – a capacitor can also be used in series but this is less common (since this alters the load voltage)
    – for examples of power factor correction see Examples 7.2 and 7.3 in the course text

    Active and Reactive Power

    When a circuit has resistive and reactive parts, the resultant power has 2 parts:
    – The first is dissipated in the resistive element. This is the active power, $P$
    –The second is stored and returned by the reactive element. This is the reactive power, $Q$ , which has units of volt amperes reactive or var

    While reactive power is not dissipated it does have an effect on the system
    – for example, it increases the current that must be supplied and increases losses with cables

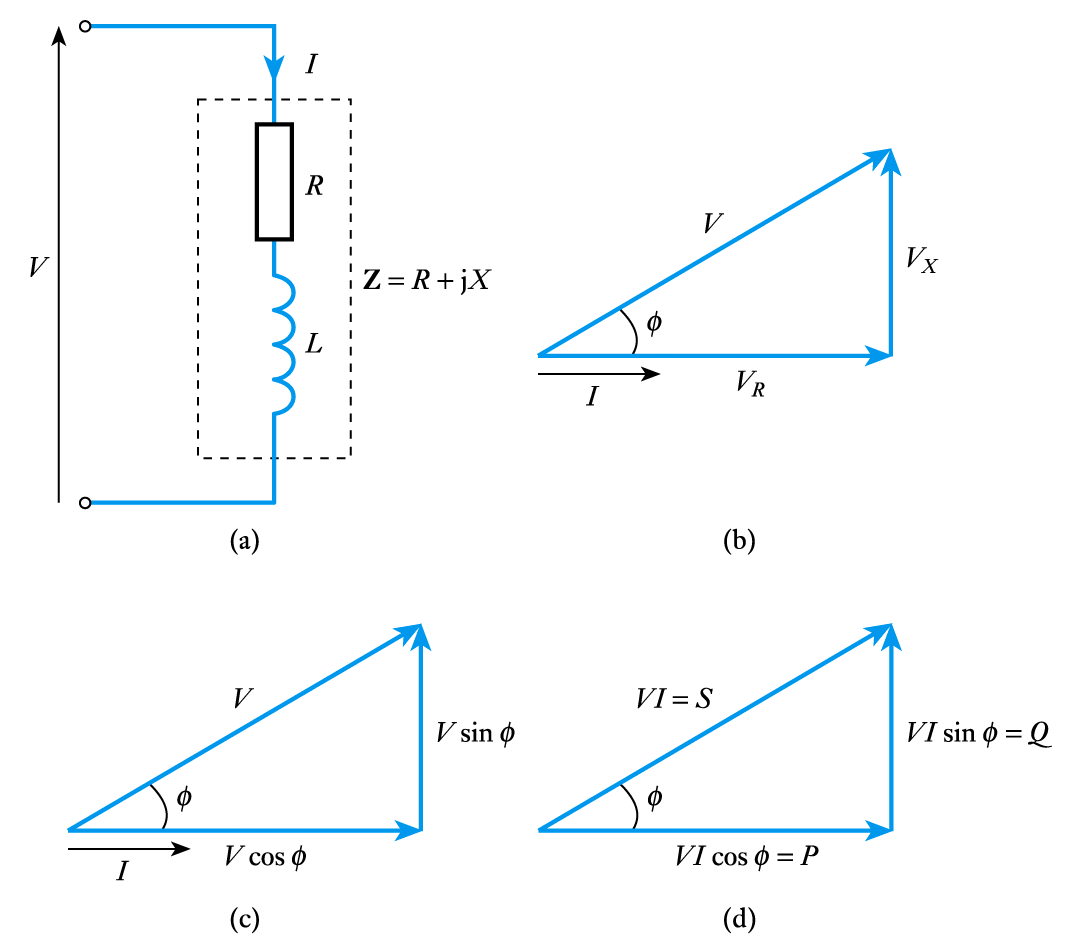
    πŸ“·   Consider an $RL$ circuit
    – the relationship between the various forms of power can be illustrated using a power triangle

    Therefore
    \begin{align*} \text{Active Power } \; P =& VI \text{ cos } \phi \; \; \; \text{ watts} \\ \\ \text{Reactive Power } \; Q =& VI \text{ sin } \phi \; \; \; \text{ var} \\ \\ \text{Apparent Power } \; S =& VI \; \; \qquad \text{ VA} \\ \\ S^2 =& p^2 + Q^2 \end{align*}

    Diagram

  • Power Measurement

    When using AC, power is determined not only by the r.m.s. values of the voltage and current, but also by the phase angle (which determines the power factor)
    – consequently, you cannot determine the power from independent measurements of current and voltage

    In single-phase systems power is normally measured using an electrodynamic wattmeter
    – measures power directly using a single meter which effectively multiplies instantaneous current and voltage

    In three-phase systems we need to sum the power taken from the various phases
    – in three-wire arrangements we can deduce the total power from measurements using $2$ wattmeter
    – in a four-wire system it may be necessary to use $3$ wattmeter
    – in balanced systems (systems that take equal power from each phase) a single wattmeter can be used, its reading being multiplied by $3$ to get the total power

    Three-Phase Systems

    So far, our discussion of AC systems has been restricted to single-phase arrangement
    – as in conventional domestic supplies

    In high-power industrial applications we often use three-phase arrangements
    – these have three supplies, differing in phase by $120^\circ$
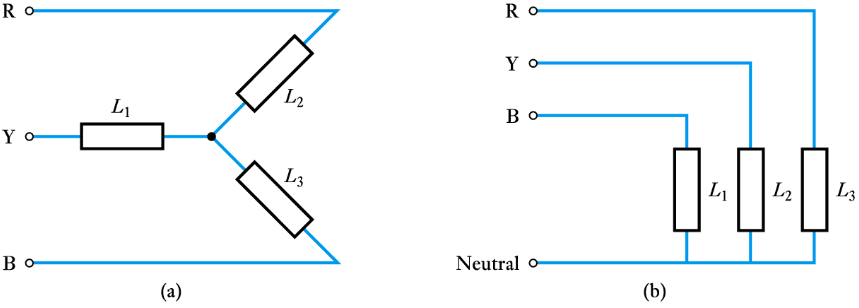
    – phases are labeled red, yellow and blue($R$, $Y$ & $B$)

    Relationship between the phases in a three-phase arrangement

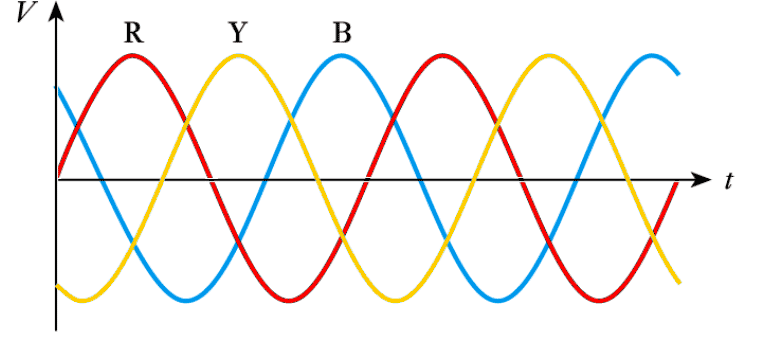
    Diagram

    πŸ“·   Three-phase arrangements may use either 3 or 4 conductors - it can be seen at this link

    Diagram

  • Further Study

    πŸŽ₯  Watch a video on power factor correction for an electric motor - Adobe Flash video

    The Further Study section at the end of Chapter 7 is concerned with power factor correction for a high-power motor.

    Your task is to calculate the size of capacitor needed to achieve a specific power factor.

    Do the sums and then watch the video at the above link.

    Key Points

    In resistive circuits the average power is equal to $VI$, where $V$ and $I$ are r.m.s. values

    In a capacitor the current leads the voltage by $90^\circ$ and the average power is zero

    In an inductor the current lags the voltage by $90^\circ$ and the average power is zero

    In circuits with both resistive and reactive elements, the average power is $VI$ cos $\phi$

    The term cos $\phi$ is called the power factor

    Power factor correction is important in high-power systems

    High-power systems often use three-phase arrangements
  • 7.15 A sinusoidal signal of $20 V$ peak at $50 Hz$ is applied to a load consisting of a $10 \Omega$ resistor and a 16 mH inductor connected in series. Calculate the power factor of this arrangement and the active power dissipated in the load.

    7.16 Determine the value of capacitor needed to be added in series with the circuit of Exercise 7.11 to produce a power factor of $1.0$. Calculate the active power that would be dissipated in the circuit with the addition of such a capacitor.

    7.17 Explain the difference between three- and four- conductor arrangements of three-phase power supplies.

    7.18 Explain why it is not possible to calculate the power dissipated in an AC network by multiplying the readings of a voltmeter and an ammeter.

    7.19 Explain how it is possible to measure power directly in a single-phase system.

    ⬇ Tutorial Solutions
    ⬇Download chapter 7 tutorial

    Exercises

    7.1 If a sinusoidal voltage with a frequency of $50 Hz$ is applied across a resistor, at what frequency does the instantaneous power supplied to the resistor vary?

    7.2 A sinusoidal voltage $v = 10 \text{ sin } 377t$ is applied to a resistor of $50 \Omega$. Calculate the average power dissipated in it.

    7.3 If a sinusoidal voltage with a frequency of $50 Hz$is applied across a capacitor, at what frequency does the instantaneous power supplied to the capacitor vary?

    7.4 A sinusoidal voltage $v = 10 \text{ sin } 377t$ is applied across a capacitor of $1 \mu F$. Calculate the average power dissipated in it.

    7.5 If a sinusoidal voltage with a frequency of $50 Hz$ is applied across an inductor, at what frequency does the instantaneous power supplied to the inductor vary?

    7.6 A sinusoidal voltage $v = 10 \text{ sin } 377t$ is applied across an inductor of $1 mH$. Calculate the average power dissipated in it.
    7.7 Explain the meanings of the terms active power, apparent power and power factor.

    7.8 The voltage across a component is $100 V$ r.m.s. and the current is $7 A$ r.m.s. If the current lags the voltage by 60Β°, calculate the apparent power, the power factor and the active power.

    7.9 Explain the difference between the units of watts, $VA$ and var.

    7.10 A sinusoidal voltage of $100 V$ r.m.s. at $50 Hz$ is applied across a series combination of a $40 \Omega$ resistor and an inductor of $100 mH$. Determine the r.m.s. current, the apparent power, the power factor, the active power and the reactive power.

    7.11 A machine operates on a $250 V$ supply at $60 Hz$; it is rated at 500 VA and has a power factor of $0.8$. Determine the apparent power, the active power, the reactive power and the current in the machine.

    7.12 Explain what is meant by power factor correction and explain why this is of importance in high-power systems.

    7.13 Calculate the value of capacitor required to be added in parallel with the machine of Exercise 7.11 to achieve a power factor of $1.0$.

    7.14 Calculate the value of capacitor required to be added in parallel with the machine of Exercise 7.11 to achieve a power factor of $0.9$.