-
1. Functions of several variables
Functions of a single variable, i.e. $y = f(x)$, are useful in representing a variety of physical phenomena. However, in many real-world situations quantities depend on more than one variable giving rise to functions of several variables. The following examples illustrate some functions of two variables:
(i). The volume $V$ of a cylinder of radius $r$ and height $h$ is given by $V = \pi \,r^2 h$. The volume $V$ therefore depends on two quantities $r$ and $h$ and if either one or both vary, $V$ varies. The variable $V$ (the dependent variable) is a function of the two variables $r$ and $h$ (the independent variables). We write $V = f(r, h)$.
(ii). The formula for the rate of flow of gas flowing turbulently in a pipe is $Q = k\,D^{1/4}T^{-5/6}$ where $k$ is a constant, $D$ is the pipe diameter and $T$ is the gas temperature. The flow rate, $Q$, is a function of the two variables $D$ and $T$, i.e. $Q = f(D,\,T)$.
(iii). The ideal gas law states that $pV = kT$ where $p$ is the pressure, $V$ is the volume and $T$ is the absolute temperature of the gas and $k$ is a constant. The equation can be rearranged to give $p = {\Large\frac{kT}{V}}$ so that the pressure $p$, is a function of the two variables $V$ and $T$, i.e. $p = f(V,\,T)$.
The graph of a function of two variables $z = f(x\,y)$ defines a surface in 3 dimensional space. The $x$ and $y$ axes define a plane, with the $z$ axis recording the height above (or below) the plane. For example, the function $z = \text{cos}(x)\text{cos}(y)$ is shown below :
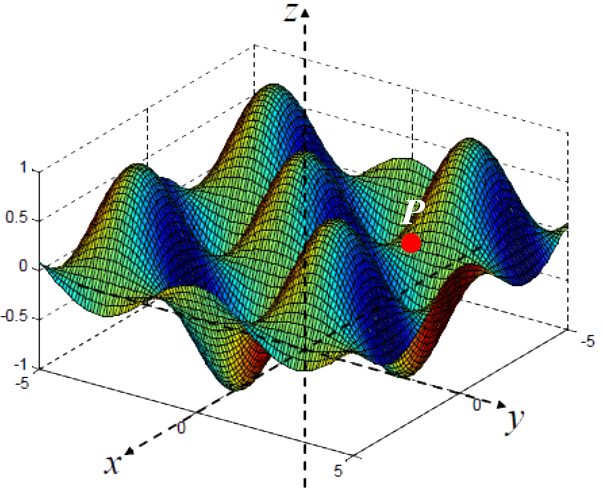
Here $z$ is the dependent variable and is a function of the two independent variables $x$ and $y$.
-
2. Partial derivatives
Consider a function of a single variable, $y = y(x)$, representing a curve in 2 dimensional space.
Calculating the derivative, ${\Large\frac{dy}{dx}}$, of $y$ with respect to $x$ enables us to determine the gradient of the tangent line to the function at a given point and hence the slope of the curve at that point. By varying the $x$ coordinate we can obtain information on how the slope of the function changes as we move in the $x$ direction.
Example
Determine the gradient of the tangent line to the function $y = x^2 - 4x + 3$ at the points $x = 0, \; x = 2$ and $x = 3$.
Solution
Calculating the derivative: ${\Large\frac{dy}{dx}} = 2x - 4$.
At $x = 0$ the gradient is, ${\Large\frac{dy}{dx}}\bigg |_{x=0} = -4$
At $x = 2$ the gradient is, ${\Large\frac{dy}{dx}}\bigg |_{x=2} = 0$
At $x = 3$ the gradient is, ${\Large\frac{dy}{dx}}\bigg |_{x=3} = 2$.
As we move in the direction of increasing $x$ the slope of the curve changes from negative (decreasing), to zero (constant), to positive (increasing).
End of ExampleFor a function of two variables however we can vary both the $x$ and $y$ coordinates and the manner in which the function changes will depend on which variable we alter. For example, imagine standing at the point $P$ in the above figure and walking directly up the hill parallel with the $x$-axis while keeping $y$ constant. Clearly the gradient will be steeper than if you were to walk to the right in a direction parallel with the $y$-axis while keeping $x$ constant. These scenarios lead us to the concept of a partial derivative of a function of two variables where we calculate the derivative of the function with respect to one variable with the other held constant.
Consider the function (surface) $z = f(x, \, y)$ in the first figure below. Suppose we keep $x$ fixed at the value $x = x_0$ and move across the surface in the direction of increasing $y$, tracing out the yellow curve as we travel. The slope of $f(x,\,y)$ changes as we move from left to right along the curve. Taking a cross-section through the surface at $x = x_0$, see the second figure below, shows this more clearly. The partial derivative of $z$ with respect to $y$, written ${\Large\frac{\partial z}{\partial y}}$, gives the slope along the curve in the $y$ direction with $x$ held constant. Note the use of ‘curly $d$’s’ in the notation for the partial derivative. Similarly, the partial derivative of $z$ with respect to $x$, written ${\Large\frac{\partial z}{\partial x}}$, gives the slope along the curve in the $x$ direction with $y$ held constant.
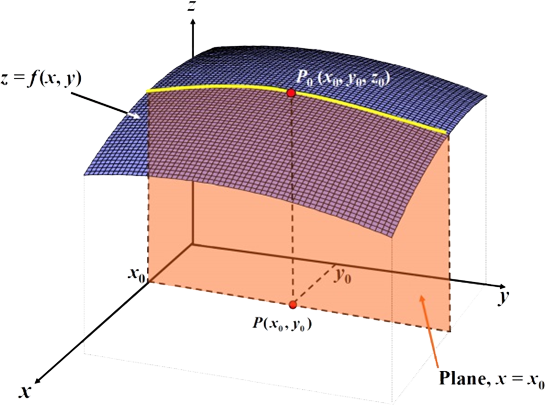
Vary $y$ while keeping $x$ constant at $x = x_0$ 
Cross-section through surface $z = f ( x,\, y )$ at $x = x_0$ showing curve $f (x_0, y)$. ${\Large\frac{\partial z}{\partial y}}$ is slope of curve $f (x_0, y)$. Summary
- Given $z = f(x,\,y)$:
- to obtain ${\Large\frac{\partial z}{\partial x}}$ differentiate $z$ with respect to $x$, treating $y$ as a constant;
Notation: ${\Large\frac{\partial z}{\partial x}} \equiv z_x \equiv {\Large\frac{\partial f}{\partial x}} \equiv f_x$. - to obtain ${\Large\frac{\partial z}{\partial y}}$ differentiate $z$ with respect to $y$, treating $x$ as a constant;
Notation: ${\Large\frac{\partial z}{\partial y}} \equiv z_y \equiv {\Large\frac{\partial f}{\partial y}} \equiv f_y$.
-
3. Calculating partial derivatives
We now illustrate, through examples, how to calculate partial derivatives of a function of two variables. An important point to note here is that no new rules of differentiation are needed so that, for example, the product, quotient and chain rules all apply as they do for functions of a single variable.
Example 1
Given $z = x^2 + 2\,x^2\,y^3 + 4y + 5$, determine ${\Large\frac{\partial z}{\partial x}}$ and ${\Large\frac{\partial z}{\partial y}}$.
Calculate ${\Large\frac{\partial z}{\partial x}}$, treating $y$ as a constant:
${\Large\frac{\partial z}{\partial x}} = {\Large\frac{\partial}{\partial x}}(x^2) + {\Large\frac{\partial}{\partial x}}(2x^2\,y^3) + {\Large\frac{\partial}{\partial x}}(4y) + {\Large\frac{\partial}{\partial x}}(5)$
$\downarrow$ $\downarrow$$\downarrow$$\downarrow$
$= 2x \;\;\;\;\;\;\;\;\;+\;\;\;\;\; 4xy^3\;\;\;\;\;\; +\;\;\;\;\; 0 \;\;\;\;\;\;+\;\; 0$
$=\;$$2x + 4y^3x$.
Calculate ${\Large\frac{\partial z}{\partial y}}$, treating $x$ as a constant:
${\Large\frac{\partial z}{\partial y}} = {\Large\frac{\partial}{\partial y}}(x^2) + {\Large\frac{\partial}{\partial y}}(2x^2\,y^3) + {\Large\frac{\partial}{\partial y}}(4y) + {\Large\frac{\partial}{\partial y}}(5)$
$\downarrow$ $\downarrow$$\downarrow$$\downarrow$
$= \;0 \;\;\;\;\;\;\;+\;\;\;\;\; 6x^2y^2\;\;\;\;\;\; +\;\;\;\;\;\, 4 \;\;\;\;\;+\;\;\;\;\, 0$
$=\;$$6x^2y^2 + 4$.
End of Example 1Example 2
Given $z = \text{sin}(x)\text{sin}(2y)$, determine ${\Large\frac{\partial z}{\partial x}}$ and ${\Large\frac{\partial z}{\partial y}}$.
Calculate ${\Large\frac{\partial z}{\partial x}}$ treating $y$, and hence $\sin(2y)$, as a constant:
${\Large\frac{\partial z}{\partial x}} = {\Large\frac{\partial}{\partial x}}[\sin(x)\sin(2y)] = \;$ $\cos(x)\sin(2y)$
Calculate ${\Large\frac{\partial z}{\partial y}}$ treating $x$, and hence $\text{sin}(x)$, as a constant:
${\Large\frac{\partial z}{\partial y}} = {\Large\frac{\partial}{\partial y}}[\sin(x)\sin(2y)] = \sin(x). 2\cos(2y) =$ $2\sin(x)\cos(2y)$.
End of Example 2Example 3
Given $z = (2x^3 + xy + y^4)^8$, determine ${\Large\frac{\partial z}{\partial x}}$ and ${\Large\frac{\partial z}{\partial y}}$.
The function $z$ is a composite function and so we use the chain rule.
Let $u = 2x^3 + xy + y^4$ so that $z = u^8$.
Note that $z$ is a function of one variable, $u$, i.e. $z = u^8$ and so we calculate the full derivative ${\Large\frac{dz}{du}}$. On the other hand, $u$ is a function of two variables, $x$ and $y$, and so we need to calculate the partial derivatives, ${\Large\frac{\partial u}{\partial x}}$ and ${\Large\frac{\partial u}{\partial y}}$.
By the chain rule,
${\Large\frac{\partial z}{\partial x}} = {\Large\frac{dz}{du}}\cdot {\Large\frac{\partial u}{\partial x}} = 8u^7 . (6x^2 + y) = \;$ $8 (2x^3 + xy + y^4)^7.(6x^2 + y)$.
Similarly, using the chain rule,
${\Large\frac{\partial z}{\partial y}} = {\Large\frac{dz}{du}}\cdot {\Large\frac{\partial u}{\partial y}} = 8u^7 . (x + 4y^3) = \;$ $8 (2x^3 + xy + y^4)^7.(x + 4y^3)$.
End of Example 3Example 4
Given $z = (x^3 + 4y^2)e^{2xy}$, obtain ${\Large\frac{\partial z}{\partial x}}$ and ${\Large\frac{\partial z}{\partial y}}$.
The function $z$ is a product of the functions $f(x,\, y) = x^3 + 4y^2$ and $g(x,\,y) = e^{2xy}$.
Recall the product rule for functions of one variable : ${\Large\frac{d}{dx}}(f\, .\, g) = f'.g + f.g'$.
Following this rule for a two-variable function, $z(x, \,y) = f(x,\,y).g(x, \,y)$ we have:
${\Large\frac{\partial z}{\partial x}} = {\Large\frac{\partial}{\partial x}}(f\, . \, g) = f_xg + fg_x$, ${\Large\frac{\partial z}{\partial y}} = {\Large\frac{\partial}{\partial y}}(f\,.\,g) = f_yg + fg_y$.
Hence,
${\Large\frac{\partial z}{\partial x}} = {\Large\frac{\partial}{\partial x}}(x^3 + 4y^2).e^{2xy} + (x^3 + 4y^2)\cdot {\Large\frac{\partial}{\partial x}}(e^{2xy})$
${\Large\frac{\partial z}{\partial x}} = 3x^2.e^{2xy} + (x^3 + 4y^2).2ye^{2xy}$
${\Large\frac{\partial z}{\partial x}} = (3x^2 + (x^3 + 4y^2).2y).e^{2xy}$
${\Large\frac{\partial z}{\partial x}} = (3x^2 + 2x^3y + 8y^3).e^{2xy}$.
Similarly,
${\Large\frac{\partial z}{\partial y}} = {\Large\frac{\partial}{\partial y}}(x^3 + 4y^2).e^{2xy} + (x^3 + 4y^2)\cdot {\Large\frac{\partial}{\partial y}}(e^{2xy})$
${\Large\frac{\partial z}{\partial y}} = 8y.e^{2xy} + (x^3 + 4y^2).2xe^{2xy}$
${\Large\frac{\partial z}{\partial y}} = (8y + (x^3 + 4y^2).2x).e^{2xy}$
${\Large\frac{\partial z}{\partial y}} = (8y + 2x^4 + 8xy^2).e^{2xy}$.
End of Example 4Example 5
Given $z = {\Large\frac{x^2\,y}{(x^2 + y^2)}}$, obtain ${\Large\frac{\partial z}{\partial x}}$ and ${\Large\frac{\partial z}{\partial y}}$.
The function $z$ is a quotient of the functions $f(x, \,y) = x^2\,y$ and $g(x,\,y) = x^2 + y^2$.
Recall the quotient rule for functions of one variable : ${\Large\frac{d}{dx}}\bigg({\Large\frac{f}{g}}\bigg) = {\Large\frac{f'g - fg'}{g^2}}$.
Following this rule for a two-variable function, $z(x,\,y) = {\Large\frac{f(x, \,y)}{g(x,\,y)}}$ we have:
${\Large\frac{\partial z}{\partial x}} = {\Large\frac{\partial}{\partial x}} \bigg({\Large\frac{f}{g}}\bigg) = {\Large\frac{f_xg - fg_x}{g^2}}$,${\Large\frac{\partial z}{\partial y}} = {\Large\frac{\partial}{\partial y}} \bigg({\Large\frac{f}{g}}\bigg) = {\Large\frac{f_yg - fg_y}{g^2}}$.
Hence,
${\Large\frac{\partial z}{\partial x}} = {\Large\frac{\frac{\partial}{\partial x}(x^2\,y).(x^2 + y^2) - x^2y\frac{\partial}{\partial x}(x^2 + y^2)}{(x^2 + y^2)^2}} = {\Large\frac{2xy(x^2 + y^2) - x^2y.2x}{(x^2 + y^2)^2}}$
${\Large\frac{\partial z}{\partial x}} = {\Large\frac{2x^3y + 2xy^3 - 2x^3\,y}{(x^2 + y^2)^2}} =\;$ ${\Large\frac{2xy^3}{(x^2 + y^2)^2}}$.
Similarly,
${\Large\frac{\partial z}{\partial y}} = {\Large\frac{\frac{\partial}{\partial y}(x^2\,y).(x^2 + y^2) - x^2y\frac{\partial}{\partial y}(x^2 + y^2)}{(x^2 + y^2)^2}} = {\Large\frac{x^2(x^2 + y^2) - x^2y.(2y)}{(x^2 + y^2)^2}}$
${\Large\frac{\partial z}{\partial y}} = {\Large\frac{x^4 + x^2y^2 - 2x^2y^2}{(x^2 + y^2)^2}} = {\Large\frac{x^4 - x^2y^2}{(x^2 + y^2)^2}} = \;$ ${\Large\frac{x^2(x^2 - y^2)}{(x^2 + y^2)^2}}$
End of Example 5Now watch the following:
📹 First Order Partial Derivatives 1
-
4. Higher order partial derivatives
For a function of a single variable, $y = y(x)$, we can differentiate the function more than once to obtain the second and higher order derivatives.
We can also calculate higher order derivatives for a function, $z = f(x,\,y)$, of two variables. The first order derivatives, ${\Large\frac{\partial z}{\partial x}}$ and ${\Large\frac{\partial z}{\partial y}}$, can be differentiated with respect to $x$ and $y$, to obtain four second order partial derivatives. The figure below summarises the procedure.
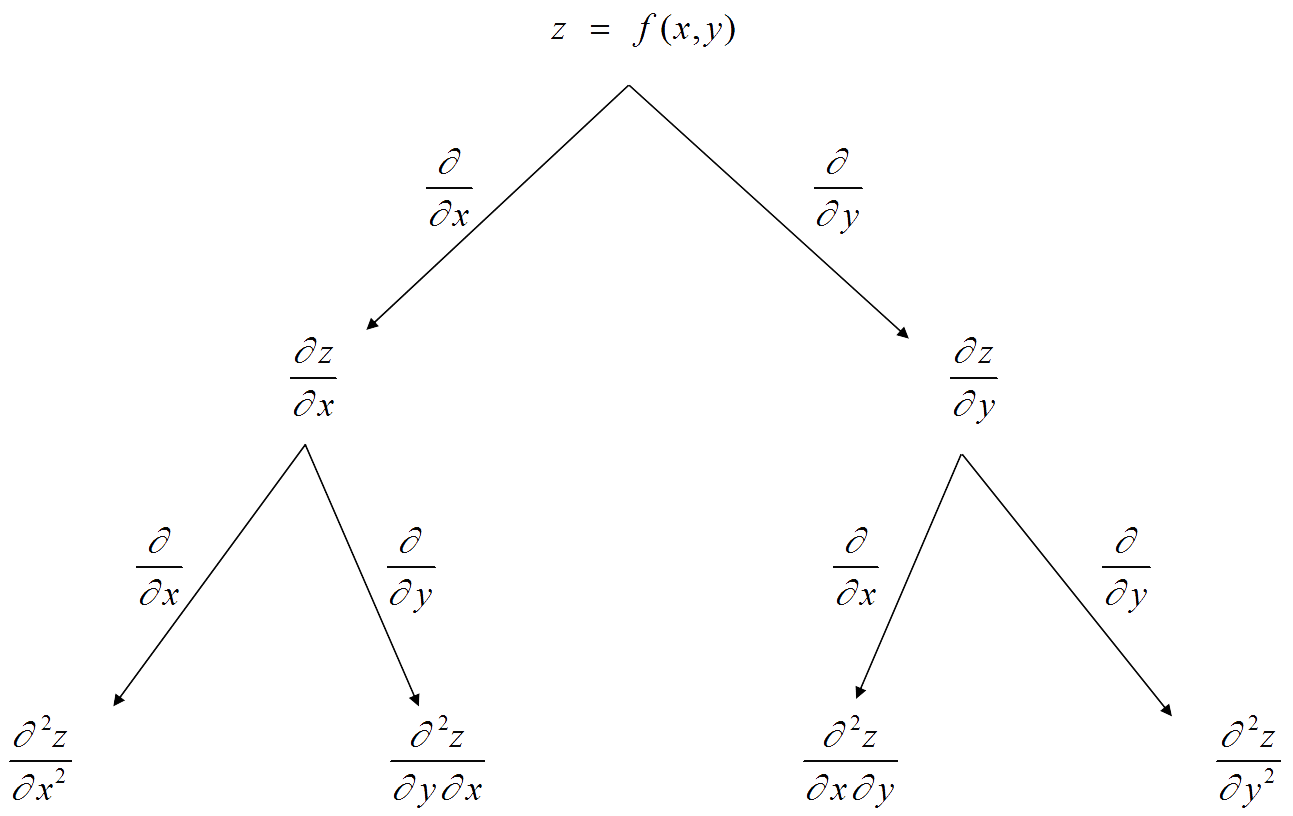
For a function, $z = f(x, \, y)$ there are a number of different ways to write the four second order partial derivatives, i.e.
${\Large\frac{\partial ^2z}{\partial x^2}} = z_{xx} = {\Large\frac{\partial ^2f}{\partial x^2}} = f_{xx}$ ${\Large\frac{\partial ^2z}{\partial y^2}} = z_{yy} = {\Large\frac{\partial ^2f}{\partial y^2}} = f_{yy}$
${\Large\frac{\partial ^2z}{\partial x \partial y}} = z_{yx} = {\Large\frac{\partial ^2f}{\partial x \partial y}} = f_{yx}$${\Large\frac{\partial ^2z}{\partial y \partial x}} = z_{xy} = {\Large\frac{\partial ^2f}{\partial y \partial x}} = f_{xy}$
We note here that if $z = f(x, \,y)$ is a function of two variables and the second order mixed partial derivatives, ${\Large\frac{\partial ^2z}{\partial x \partial y}}$ and ${\Large\frac{\partial ^2z}{\partial y \partial x}}$, both exist and are continuous then they will be equal, i.e. ${\Large\frac{\partial ^2z}{\partial x \partial y}} = {\Large\frac{\partial ^2z}{\partial y \partial x}}$.
Example 6
Given $z = x^2 + e^{xy}$ find ${\Large\frac{\partial ^2z}{\partial x^2}}$, ${\Large\frac{\partial ^2z}{\partial y^2}}$, ${\Large\frac{\partial ^2z}{\partial x \partial y}}$ and ${\Large\frac{\partial ^2z}{\partial y \partial x}}$.
${\Large\frac{\partial z}{\partial x}} =$ $2\,x + y\,e^{xy}$${\Large\frac{\partial z}{\partial y}} = 0 + xe^{xy} = $ $xe^{xy}$
${\Large\frac{\partial ^2z}{\partial x^2}} \equiv {\Large\frac{\partial}{\partial x}}\bigg ({\Large\frac{\partial z}{\partial x}}\bigg) = {\Large\frac{\partial}{\partial x}}(2\,x + y\,e^{xy}) = $ $2 + y^2e^{xy}$
${\Large\frac{\partial ^2z}{\partial y^2}} \equiv {\Large\frac{\partial}{\partial y}}\bigg({\Large\frac{\partial z}{\partial y}}\bigg) = {\Large\frac{\partial}{\partial y}}(x\,e^{xy}) = $ $x^2e^{xy}$
${\Large\frac{\partial ^2z}{\partial x \partial y}} \equiv {\Large\frac{\partial}{\partial x}}\bigg({\Large\frac{\partial z}{\partial y}}\bigg) = {\Large\frac{\partial}{\partial x}}(x\,e^{xy}) = 1.e^{xy} + x.y\,e^{xy}$ (using the Product rule)
${\Large\frac{\partial ^2z}{\partial x \partial y}} =$ $e^{xy}(1 + x\,y)$
${\Large\frac{\partial ^2z}{\partial y \partial x}} \equiv {\Large\frac{\partial}{\partial y}}\bigg({\Large\frac{\partial z}{\partial x}}\bigg) = {\Large\frac{\partial}{\partial y}}(2\,x + y\,e^{xy}) = 0 + 1.e^{xy} + y.xe^{xy}$ (using the Product rule on $y\,e^{xy})$
${\Large\frac{\partial ^2z}{\partial y \partial x}} = $ $e^{xy}(1 + x\,y)$.
Note that, as expected, the mixed partial derivatives are equal i.e., $z_{xy} = z_{yx}$.
End of Example 6Now watch the following:
-
Summary
This unit has extended the idea of differentiation of a function of one variable and introduced the concept of a partial derivative of a function of two variables.
- You should now be able to:
- understand the meaning of a partial derivative.
- determine partial derivatives, up to second order, of a function of two variables.
- apply standard rules of differentiation ( chain rule, product rule and quotient rule ) to calculate the partial derivatives of a function of two variables.
In the next unit we introduce ordinary differential equations (ODEs) and consider different types of ODEs and methods for their solution.