-
1. Introduction
For functions of a single variable there are two types of integration. The first is indefinite integration,
$$I = \int f(x)\,dx = F(x) + C,$$
which is effectively “differentiation in reverse”, and the second is definite integration,
$$I = \int _a^b f(x)\,dx = F(b) - F(a).$$
Before we consider how to integrate functions of two variables, we shall consider the “construction” of definite integrals and extend this idea to double integrals.
-
2. Definite Integrals - Functions of a Single Variable
Recall that one interpretation of a definite integral of the form,
$$I = \int_a^b f(x)\,dx$$
is an area between the graph of $y = f(x)$ and the $x$-axis. Let us examine this interpretation a little more closely.
If we were looking to determine the area limited by $x = a$ and $x = b$ we might approximate it first. Let us divide the interval $[\,a,\,b\,]$ into $n$ strips of width $\delta x$ and form rectangles whose heights are determined by the function $y = f(x)$ as shown in the following diagram:
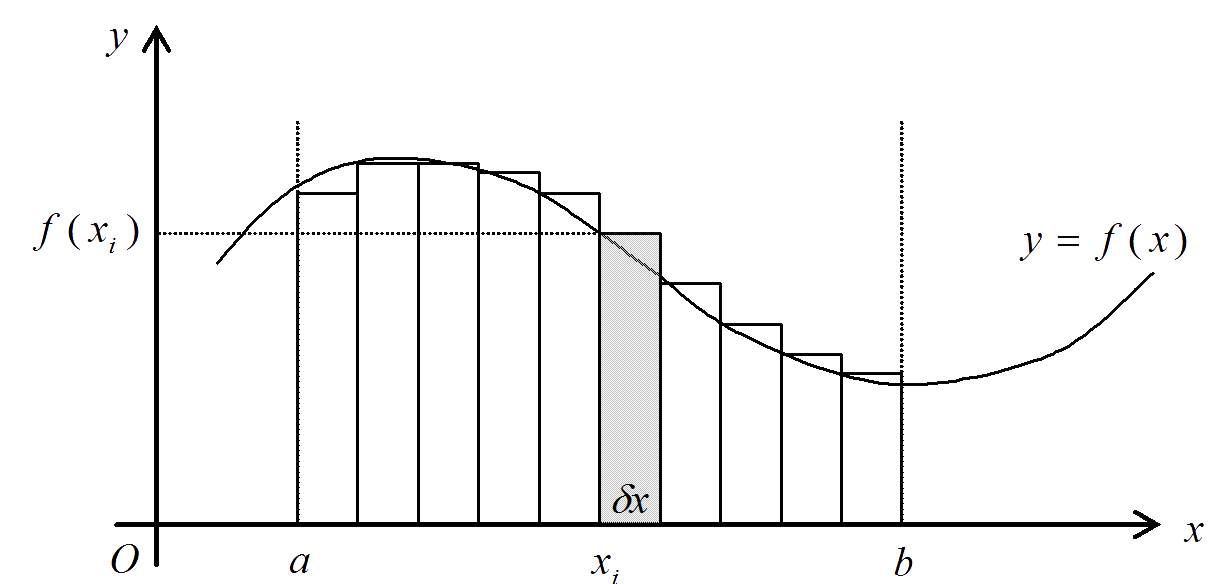
The area of a typical rectangle (shaded grey) is given by,
$$\delta A = f(x_i)\,\delta\, x $$
where $f(x_i)$ is the height of the rectangle and $\delta\,x$ is its width.
The total area is approximated by summing the areas of all $n$ rectangles,
$$A \equiv \sum_{i=1}^{n}f(x_i)\,\delta\,x. \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;[\,1\,] $$
If we take a smaller $\delta\,x$ ( larger $n$ ) the approximation should improve. Taking the limit as $\delta\,x \rightarrow 0$ (equivalently letting $n \rightarrow \infty$ ), it can be shown that,
$$A = \int _a^b f(x)\,dx. \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;[\,2\,]$$
-
3. Double Integrals Over Rectangular Regions
Suppose we have a function of two variables, $z = f(x\,y)$ defined over a rectangular region, $R$, whose sides are parallel with the coordinate axes in the $xy$ – plane, i.e. $R = \{\,(x,\,y) : a \le x \le b,\, c \le y \le d \,\}$ as shown in the figure below.
Consider partitioning $R$ into small rectangles $R_{i\,j}$ , where $1 \le i \le n$ and $ 1 \le j \le m$. Each small rectangle has area $\delta A = \delta\,x \delta\,y$. Here we have partitioned the interval $a \le x \le b$ into $n$ subintervals of width $\delta\,x$ and the interval $c \le y \le d$ into $m$ subintervals of width $\delta\,y$, as shown below.
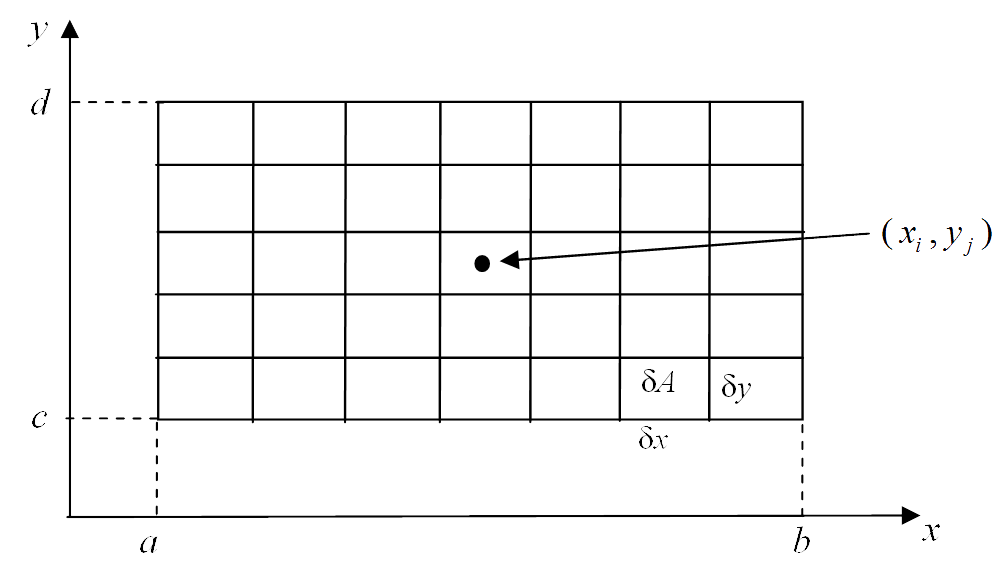
Choose an arbitrary point $(x_i,\,y_j)$ in rectangle $R_{i\,j}$ and project the rectangle up to the function surface to form a “cuboidal” volume element of height $f(x_i,\,y_j)$, as shown:
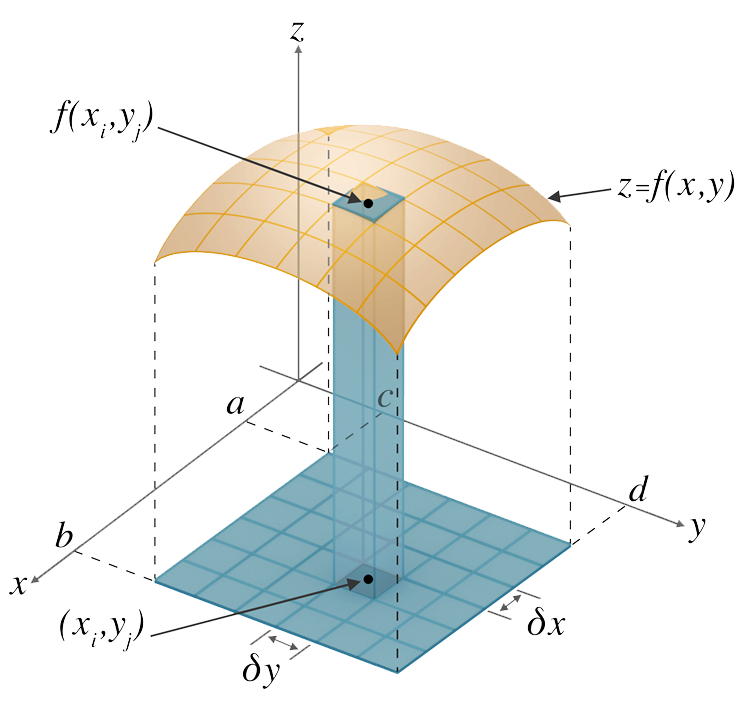
The volume of this column is given by $f(x_i, \,y_j)\delta A = f(x_i,\;y_j)\,\delta\,x\,\delta\,y$. This value will be an approximation to the exact volume above the small rectangular area $\delta A$ since the height of the column varies over the small rectangular area.
The volume above the entire region $R$ in the $xy$ - plane and under the surface $z = f(x,\,y)$, shown in the figure below, can be approximated by summing the volumes of all the cuboids, i.e.
$$V \equiv \sum_{i=1}^{n} \sum_{j=1}^{m} f(x_i,\,y_j)\,\delta A = \sum_{i=1}^{n} \sum_{j=1}^{m} f(x_i,\,y_j)\,\delta\,y\,\delta\,x.$$
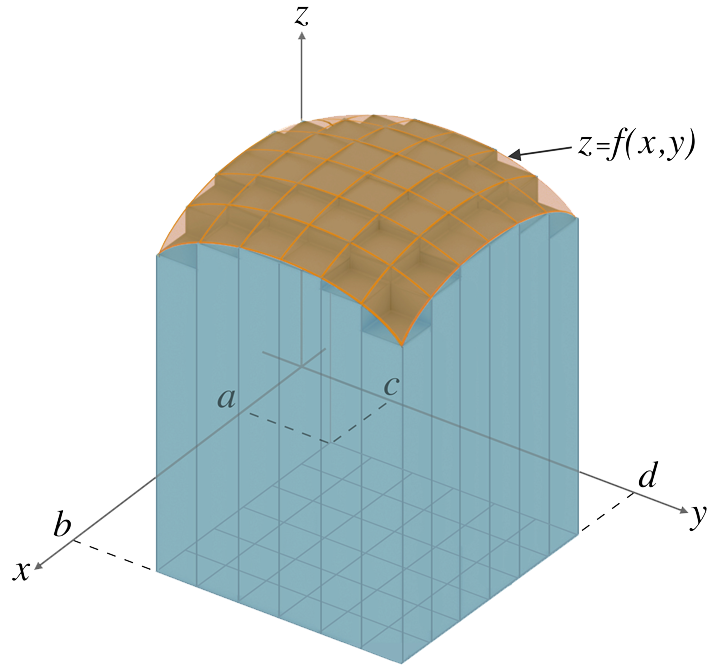
By taking the limit as $\delta\,y,\,\delta\,x \rightarrow 0 \;(\,m, n \rightarrow \infty\,)\;$ we obtain the double integral, i.e.
$$\overset{\Large\lim\;\;\;\;\;\;\;\;}{\delta\,x,\,\delta\,y \rightarrow 0} \Bigg(\sum_{i=1}^{n} \sum_{j=1}^{m} f(x_i,\,y_j)\,\delta\,y\,\delta\,x \Bigg) = \iint\limits_{R} f(x,\,y)\,dA = \iint\limits_{R} f(x,\,y)\,dy\;dx.$$
Referring to the above figure we can write $V = {\Large\iint\limits_{R}} f(x,\,y)\,dy\,dx$ as the iterated integral
$$\int_{x=a}^{x=b} \int_{y=c}^{y=d} f(x,\,y)\,dy\,dx = \int_{x=a}^{x=b} \Bigg(\int_{y=c}^{y=d} f(x,\,y)\,dy\,\Bigg)\,dx.$$
This integral is calculated from the ‘inside out’. First we integrate $f(x,\,y)$ with respect to $y$, treating $x$ as a constant, and evaluate from $y = c$ to $y = d$. This calculation gives a function of $x$ only, which is then integrated from $x = a$ to $x = b$.
Now watch the following:
📹 Introduction to Double Integrals and Volume 1
📹 Introduction to Double Integrals and Volume 2
We now illustrate the process by means of an example.
Example 1
Determine the volume of the solid that lies under the plane $z = 5 - x - y$ and above the rectangular region, $R = \{(x,\,y) : 0 \le x \le 2,\; 0 \le y \le 1\,\}$.
Solution
Here $f(x,\,y) = 5 - x - y$ and, from above, $V = {\Large\iint\limits_{R}}\,(5 - x - y)\,dy\,dx$.
The limits $a = 0, \; b = 2, \; c = 0, \; d = 1$ for the region $R$ are inserted to give $V = {\huge\int}_{x = 0}^{x = 2}\;{\huge\int}_{y = 0}^{y = 1} (5 - x - y)dy\,dx$.
First evaluate the inner integral, treating $x$ as a constant,
$$\int_{y=0}^{y=1}(5 - x - y)\,dy = \bigg[5\,y - x\,y - \frac{1}{2}y^2\bigg]_{y=0}^{y=1}$$
$= \bigg( 5 - x - {\Large\frac{1}{2}}\bigg) - 0 =\;$ ${\Large\frac{9}{2}} - x$.
Now evaluate the outer integral to obtain the required volume, i.e.
$V = {\huge\int}_{x=0}^{x=2} \bigg({\Large\frac{9}{2}} - x \bigg)dx = \bigg[{\Large\frac{9}{2}}x - {\Large\frac{1}{2}}x^2\bigg]_{x=0}^{x=2} = (9 - 2) - (0) =\;$ $7$.
The value, 7, represents the volume of the solid that lies under the plane $z = 5 - x - y$ and above the rectangular region, $R = \{(x,\,y) : 0 \le x \le 2, \; 0 \le y \le 1\,\}$.
End of Example 1In the next example we investigate what happens when the order in which the integrations are performed, over a rectangular region $R$, is changed. We first integrate the function in Example 1 with respect to $x$, treating $y$ as a constant, and then integrate the resulting function of $y$ only with respect to $y$.
Example 2
Changing the order in which the iterated integral in Example 1 is evaluated gives:
$$V = \int_{y=0}^{y=1} \int_{x=0}^{x=2} (5 - x - y)\,dx\,dy.$$
Solution
First evaluate the inner integral, treating $y$ as a constant,
$$\int_{x=0}^{x=2}(5 - x - y)\,dx = \bigg[\,5\,x - \frac{1}{2}x^2 - y\,x\, \bigg]_{x=0}^{x=2} $$
$= (10 - 2 - 2\,y) - (0) =\;$ $8 - 2\,y$.
Now evaluate the outer integral,
${\huge\int}_{y=0}^{y=1} (8 - 2\,y)\,dy = \;\Big[8\,y - y^2\,\Big]_{y=0}^{y=1} = (8 - 1) - (0) = \;$ $7$.
The value of 7 represents the volume of the solid below the surface $z = 5 - x - y$ and above the rectangular region $R = \{(x,\,y) : 0 \le x \le 2, \; 0 \le y \le 1 \}$. This result agrees with the value obtained in Example 1. Hence, we have shown that
$$\iint\limits_{R} (5 - x - y)\,dy\,dx = \iint\limits_{R} (5 - x - y)\,dx\,dy.$$
In general, when the region we are integrating over is rectangular the order of integration does not matter and both integrals evaluate to the same value (volume).
Note: The result ${\Large\iint\limits_{R}} f(x,\,y)\,dy\,dx = {\Large\iint\limits_{R}} f(x, \,y)\,dx\,dy$ is always true provided $f(x,\,y)$ is a continuous function.
The evaluation of double integrals using iterated integrals is now considered over regions of integration which are not rectangular.
End of Example 2Now watch the following:
-
4. Double Integrals Over General Regions
In the previous section we looked at double integrals over rectangular regions. However, most regions are not rectangular and we therefore need to consider integrals of the form
${\Large\iint\limits_{R}} f(x,\,y)\,dA $
where $R$ is any region. Here we consider two types of planar regions identified as Type 1 and Type 2.
A planar region $R$ is said to be of TYPE 1 if it lies between the graphs of two continuous functions of $x$, that is, $R = \{(x,\,y) : a \le x \le b, \;\, l(x) \le y \le u(x)\,\}$. Hence, as shown in the figure below, $y$ ranges from the function $y = l(x)$ up to the function $y = u(x)$ while $x$ ranges between the constant values $x = a$ and $x = b$.

A region is of Type 1 if any VERTICAL SCANNING LINE, $x = k$, in the interval $a < x < b$, intersects the boundary of $R$ in at most two points. Type 1 regions are also known as vertically simple regions.
If $f(x,\,y)$ is continuous on a Type 1 region $R$, then the double integral $\iint\limits_{R} f(x,\,y)\,dA$ can be described by the iterated integral
$$\int_{x=a}^{x=b} \bigg\{\int_{y=l(x)}^{y=u(x)}f(x,\,y)\,dy\bigg\}\,dx \;\;\text{or as} \;\; \int_{a}^{b}\int_{l(x)}^{u(x)}f(x,\,y)\,dy\,dx.$$
As before, the inner integral is evaluated first. The integration of $f(x,\,y)$ is carried out with respect to $y$, treating $x$ as a constant. The inner integral will produce an expression in $x$ only. The value of the double integral is then obtained by integrating this expression with respect to $x$.
A planar region $R$ is said to be of TYPE 2 if it lies between the graphs of two continuous functions of $y$, that is, $R = \{(x,\,y) : L(y) \le x \le U(y), \;\, c \le y \le d \,\}$. Hence, $x$ ranges from the function $x = L(y)$ up to the function $x = U(y)$ while $y$ ranges between the constant values $y = c$ and $y = d$.
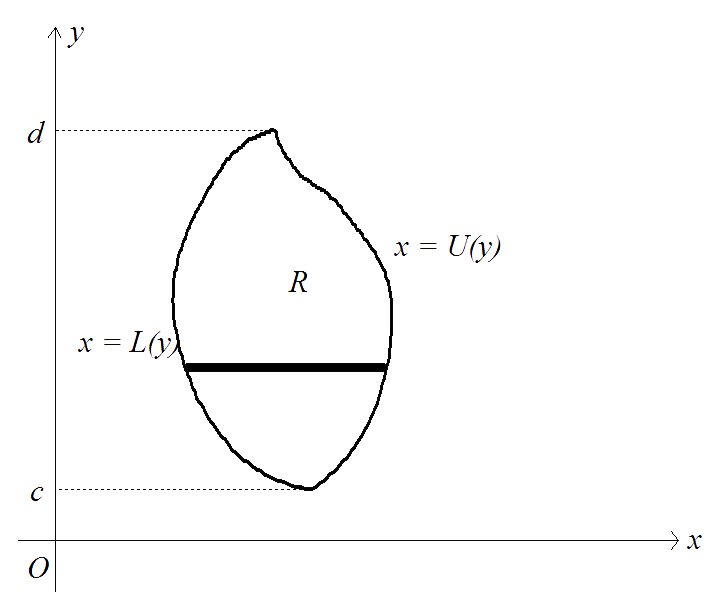
A region is of Type 2 if any HORIZONTAL SCANNING LINE, $y = k$, in the interval $c < y < d$, intersects the boundary of $R$ in at most two points. Type 2 regions are also known as horizontally simple regions.
If $f(x,\,y)$ is continuous on a Type 2 region $R$, then the double integral $\iint\limits_{R} f(x,\,y)\,dA$ can be described by the iterated integral
$$\int_{y=c}^{y=d} \Bigg\{\int_{x=L(y)}^{x=U(y)}f(x,\,y)\,dx \Bigg\}\; dy \;\;\text{or as}\;\; \int_{c}^{d} \int_{L(y)}^{U(y)} f(x,\,y)\,dx\,dy.$$
As before the inner integral is evaluated first. The integration of $f(x,\,y)$ is carried out with respect to $x$ treating $y$ as a constant. The inner integral will produce an expression in $y$ only. The value of the double integral is then obtained by integrating this expression with respect to $y$.
In some cases, such as for rectangular regions, we can describe the region $R$ as either Type 1 or Type 2, so that ,
$$\iint\limits_{R} f(x,\,y)\,dA = \int_{a}^{b} \int_{l(x)}^{u(x)} f(x,\,y)\,dy\,dx = \int_{c}^{d} \int_{L(y)}^{U(y)} f(x, \,y)\,dx\,dy.$$
Example 3
Describe the double integral ${\Large\iint\limits_{R}} x^2\,y\,dA$ where $R$ is the triangular region in the $xy$ - plane bounded by the lines $x = 0$ , $y = 1$ and $y = x$ as an iterated integral and hence evaluate.
Solution
Consider $R$ as a Type 1 region, with a vertical scanning line, as shown below.
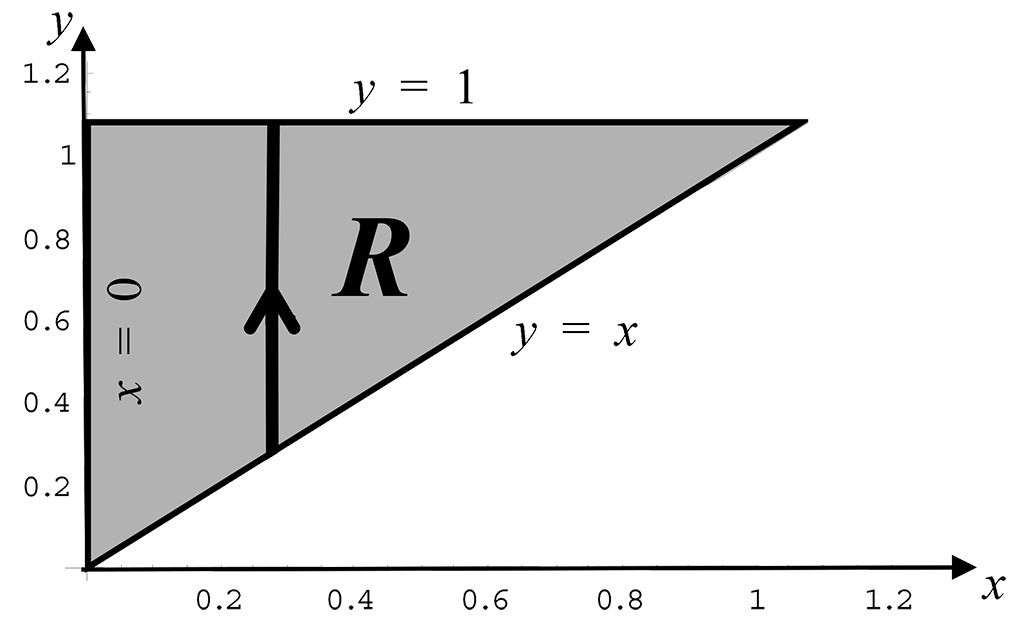
From the direction of the arrow we see that the vertical scanning line starts at the line $y = x$, giving the lower limit of integration, and ends at the line $y = 1$, giving the upper limit of integration. Vertical scanning lines are summed over $R$ from $x = 0$ to $x = 1$.
Hence,
$y$ ranges from $y = x$ to $y = 1$ and
$x$ ranges from $x = 0$ to $x = 1$.
The integral is then given by
$$\iint\limits_{R} x^2\,y\,dA = \int_{x=0}^{x=1}\,\int_{y=x}^{y=1} x^2\,y\,dy\,dx$$
which we evaluate as follows:
Inner integral
${\huge\int}_{y=x}^{y=1} x^2\,y\,dy$ ( along the vertical scanning line, $x$ is constant )
$= \bigg[{\Large\frac{x^2\,y^2}{2}}\bigg]_{y=x}^{y=1} = \bigg({\Large\frac{x^2.1^2}{2}}\bigg) - \bigg({\Large\frac{x^2.x^2}{2}}\bigg) =\;$ ${\Large\frac{x^2}{2}} - {\Large\frac{x^4}{2}}$.
Outer integral
${\huge\int}_{x=0}^{x=1}\bigg({\Large\frac{x^2}{2}} - {\Large\frac{x^4}{2}}\bigg)\,dx \;\;\;\;\;\;\;\;\;\; = \bigg[{\Large\frac{x^3}{6}} - {\Large\frac{x^5}{10}} \bigg ]_{x=0}^{x=1}$.
$= \bigg( {\Large\frac{1}{6}} - {\Large\frac{1}{10}} \bigg) - (0) = \;$ ${\Large\frac{1}{15}}$.
The value of ${\Large\frac{1}{15}}$ represents the volume under the surface $z = x^2\,y$ and above the triangular region, $R$.
End of Example 3Example 4
Evaluate the integral in Example 3 by considering the region of integration, $R$, as a Type 2 region.
Solution
Consider $R$ as a Type 2 region, with horizontal scanning lines, as shown below:
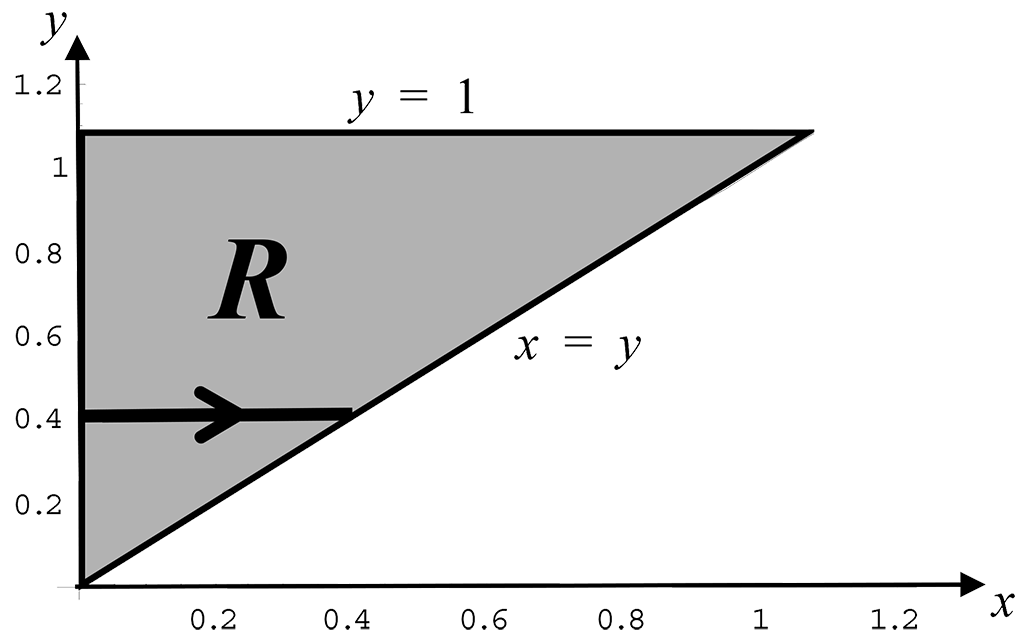
From the direction of the arrow we see that the horizontal scanning line starts at the line $x = 0$, giving the lower limit of integration, and ends at the line $x = y$, giving the upper limit of integration. Horizontal scanning lines are summed over $R$ from $y = 0$ to $y = 1$. Hence,
$x$ ranges from $x = 0$ to $x = y$ and
$y$ ranges from $y = 0$ to $y = 1$.
The integral is then given by
$$ \iint\limits_{R} x^2\,y\,dA = \int_{y=0}^{y=1} \,\int_{x=0}^{x=y}x^2\,y\,dx\,dy,$$
which we evaluate as follows:
Inner integral
${\huge\int}_{x=0}^{x=y} x^2\,y\,dx$ ( along the horizontal scanning line, $y$ is constant )
$= \bigg[{\Large\frac{x^3\,y}{3}}\bigg]_{x=0}^{x=y} = \bigg({\Large\frac{y^3\,y}{3}}\bigg) - (0) =\;$ ${\Large\frac{y^4}{3}}$.
Outer integral
${\huge\int}_{y=0}^{y=1} {\Large\frac{y^4}{3}}dy = \bigg[{\Large\frac{y^5}{15}}\bigg]_{y=0}^{y=1} = {\Large\frac{1}{15}} - 0 =\; $ ${\Large\frac{1}{15}}$.
This result agrees with the answer obtained in Example 3.
NOTES
(i). The outside limits of integration are ALWAYS constant values – they are NEVER variable limits.
(ii). The limits of integration for the iterated integral are found from a sketch of the region, $R$. ALWAYS SKETCH THE REGION, $R$.
End of Example 4Sometimes, as shown in the following example, the order in which we perform the integration, i.e. whether we consider the region as Type 1 or Type 2 can save us a considerable amount of work and thereby reduce the likelihood of errors. It is therefore essential to produce a sketch to help identify the most efficient approach.
Now watch the following:
📹 Double Integrals over General Regions 1
📹 Double Integrals over General Regions 2
Example 5
Determine ${\Large\iint\limits_{R}}(x + y)\,dA$ where $R$ is the region enclosed by $y = x^2$ and $y = x + 2$ .
Solution
To determine the limits of integration we must first sketch the region $R$.
The parabola $y = x^2$ and the line $y = x + 2$ intersect when,
$x^2 = x + 2$
$x^2 - x - 2 = 0$
$(x + 1)(x - 2) = 0$
$x = -1\,, \,x = 2$.
Points of intersection of the parabola and line are, $(-1,\,1)$ and $(2,\,4)$.
Method 1
Suppose we consider $R$ as a Type 1 region, with a vertical scanning line, as shown below:
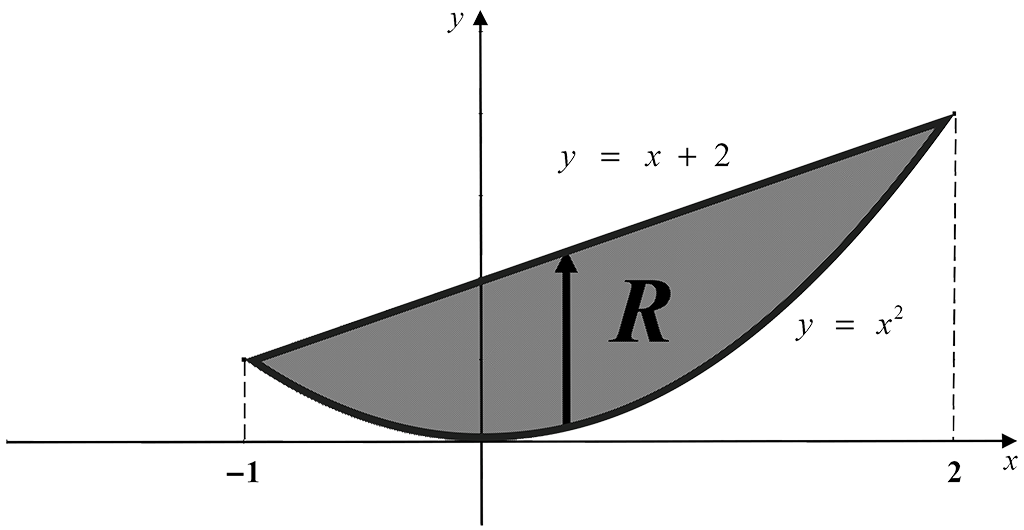
The vertical scanning line starts at $y = x^2$ and ends at $y = x + 2$ giving the lower and upper limits of integration respectively. Also, $x$ ranges from $x = -1$ to $x = 2$ .
The integral is therefore given by
$$\iint\limits_{R}( x + y)\,dA = \int_{x = -1}^{x = 2}\,\int_{y = x^2}^{y = x + 2} (x + y)\,dy\,dx.$$
Inner integral
${\huge\int}_{y=x^2}^{y=x+2}\, (x + y)\,dy$ (along the vertical scanning line, $x$ is constant)
$= \bigg[x\,y + {\Large\frac{1}{2}}y^2 \,\bigg]_{y=x^2}^{y=x+2} = \bigg( x(x + 2) + {\Large\frac{1}{2}}(x + 2)^2\,\bigg) - \bigg(x^3 + {\Large\frac{1}{2}}x^4\,\bigg)$
$= \;$ $-{\Large\frac{1}{2}}x^4 - x^3 + {\Large\frac{3}{2}}x^2 + 4x + 2$.
Outer integral
${\huge\int}_{x = -1}^{x = 2} \bigg(-{\Large\frac{1}{2}}x^4 - x^3 + {\Large\frac{3}{2}}x^2 + 4x + 2\,\bigg)\,dx$
$= \bigg[-{\Large\frac{1}{10}}x^5 - {\Large\frac{1}{4}}x^4 + {\Large\frac{1}{2}}x^3 + 2x^2 + 2x \,\bigg]_{x = -1}^{x = 2}$
$= \bigg(-{\Large\frac{32}{10}} - 4 + 4 + 8 + 4\,\bigg) - \bigg({\Large\frac{1}{10}} - {\Large\frac{1}{4}} - {\Large\frac{1}{2}} + 2 - 2 \bigg) = \;$ ${\Large\frac{189}{20}}$.
Method 2
Suppose we now consider $R$ as a Type 2 region, with a horizontal scanning line. This approach however, involves considerably more effort on our part as we are required to evaluate two iterated integrals. As shown in the figure below the region $R$ has to be split into sub-regions, $R_1$ and $R_2$, due to a horizontal scanning line starting on different curves in the two regions.
In region $R_1$ where $0 \le y \le 1$, the scanning line starts on $x = -\sqrt{y}\;$ (i.e. $y = x^2$ ) while in region $R_2$, where $1 \le y \le 4$, the scanning line starts on $x = y - 2\;$ (i.e. $y = x + 2$ ). The integral needs to be evaluated over each sub-region and the results added together.
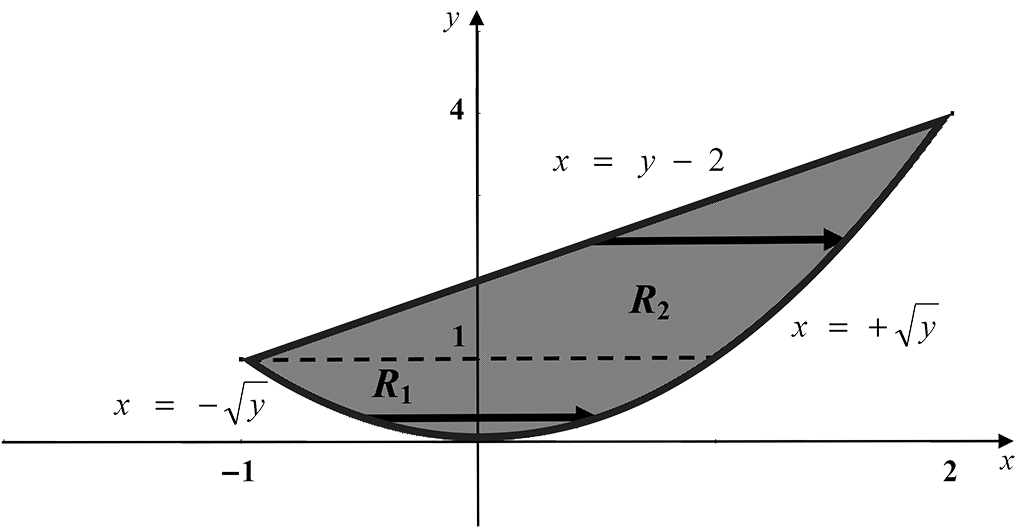
The double integral ${\Large\iint\limits_{R}}\,(x + y)\,dx\,dy$ over region $R_1$ is described by the iterated integral,
$$I_1 = \int_{y=0}^{y=1}\,\int_{x = - \sqrt{y}}^{x = \sqrt{y}}\,(x + y)\,dx\,dy.$$
The double integral ${\Large\iint\limits_{R}}\,(x + y)\,dx\,dy$ over the region $R_2$ is described by the iterated integral
$$I_2 = \int_{y = 1}^{y = 4}\,\int_{x = y - 2}^{x = \sqrt{y}}\,(x + y)\,dx\,dy.$$
We leave you to show that when evaluated, $I_1 = {\Large\frac{4}{5}}$ and $I_2 = {\Large\frac{173}{20}}$.
Hence, using horizontal scanning lines
${\Large\iint\limits_{R}}\; (x + y)\,dx\,dy = I_1 + I_2 = {\Large\frac{4}{5}} + {\Large\frac{173}{20}} = \;$ ${\Large\frac{189}{20}}$, as obtained earlier.
Note that in this case a sketch has helped us identify that calculations are made significantly easier by using a Type 1 region, resulting in a ‘$dy\,dx$ integral’, as opposed to a Type 2 region, giving a ‘$dx\,dy$ integral’. In the next section we look at changing the order of integration a useful technique when integrating in a given order is complicated or even impossible to carry out directly. One of the main challenges in such situations is identifying the limits of integration and so it is essential to sketch the region to enable calculations to be performed in the most efficient manner.
End of Example 5 -
5. Changing the Order of Integration
In some problems an iterated integral may be cumbersome to evaluate (as in Example 5 with horizontal scanning lines) or, in other cases, even impossible to evaluate. In these instances it will be worthwhile to consider the other iterated integral – this technique is called CHANGING THE ORDER OF INTEGRATION.
Example 6
By changing the order of integration, evaluate, $I = {\huge\int}_{y=0}^{y=1}\,{\huge\int}_{x=y}^{x=1}\,e^{x^2}\,dx\,dy$.
Solution
The change of order is necessary here since ${\huge\int} e^{x^2}dx$ cannot be evaluated.
The procedure is to first sketch the region $R$ from the limits on the given iterated integral.
In this case we have the following limits:
$x$: ranges from $x = y$ to $x = 1$
$y$: ranges from $y = 0$ to $y = 1$.
The inner integral is with respect to $x$ (Type 2 region) so that the scanning line is horizontal starting on the line $x = y$ (or $y = x$) and finishing on the line $x = 1$ as shown below.
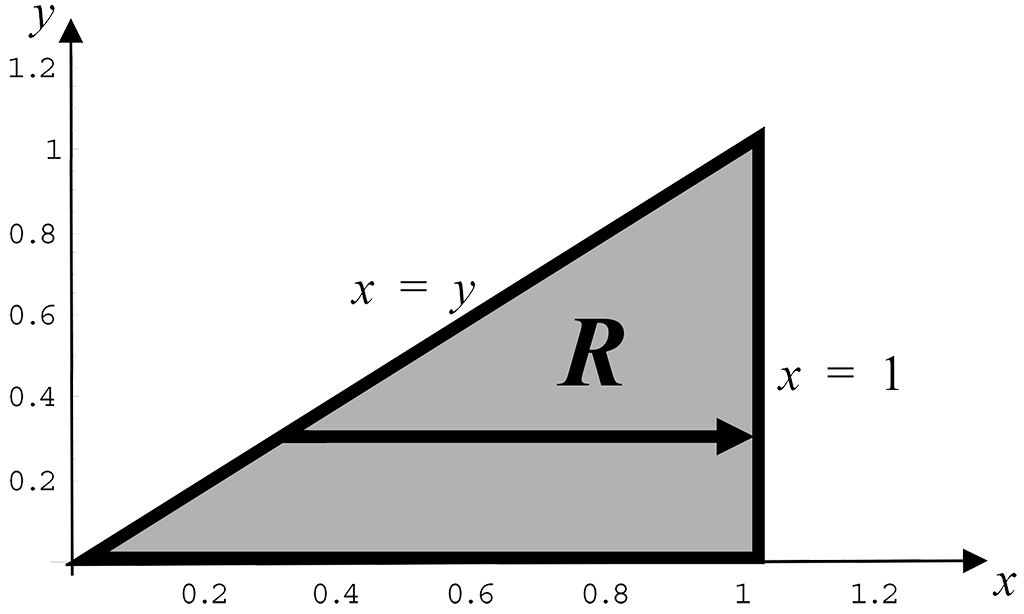
As noted above however it is not possible to evaluate the iterated integral as a Type 2 and so we are going to change (reverse) the order of integration to describe the region as Type 1 and integrate with respect to $y$ first, followed by an integration with respect to $x$.
As we are now considering $R$ as a Type 1 region we use vertical scanning lines.
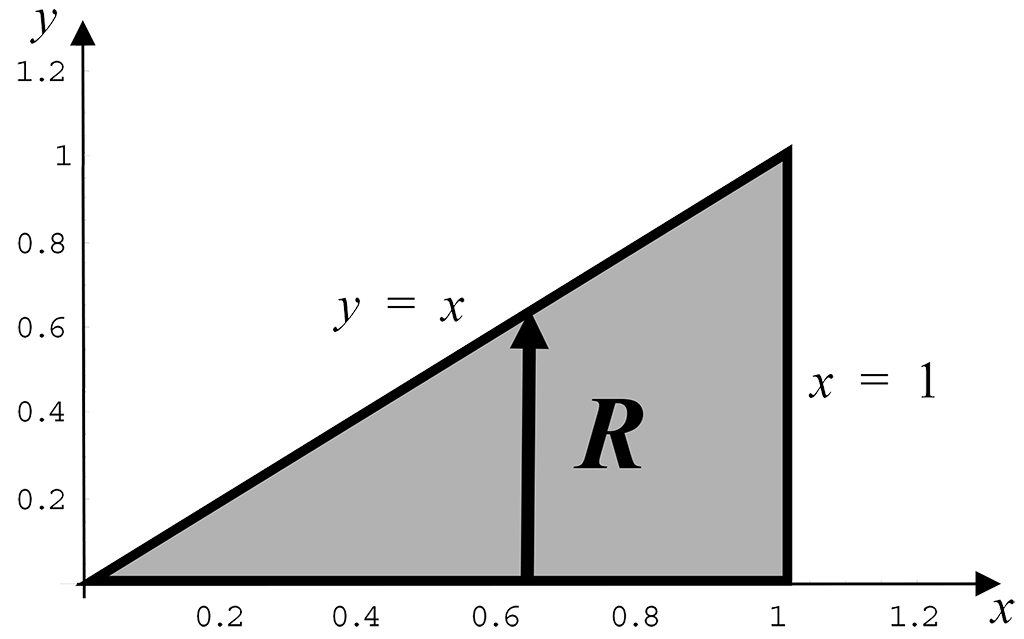
In this case we have the following limits:
$y$: ranges from $y = 0$ to $y = x$
$x$: ranges from $x = 0$ to $x = 1$.
The integral ${\huge\int}_{y=0}^{y=1}\,{\huge\int}_{x=y}^{x=1}e^{x^2}\,dx\,dy$ with the order reversed is therefore, $I = {\huge\int}_{x = 0}^{x = 1}\,{\huge\int}_{y = 0}^{y = x}e^{x^2}\,dy\,dx$.
Evaluating the integral gives,
Inner integral
${\huge\int}_{y=0}^{y=x}e^{x^2}dy = \bigg[e^{x^2}y\bigg]_{y=0}^{y=x} = x\,e^{x^2} - 0 =\;$ $x\,e^{x^2}$.
Outer integral
${\huge\int}_{0}^{1}x\,e^{x^2}\,dx$
Use the substitution, $u = x^2 \Rightarrow {\Large\frac{du}{dx}} = 2x \Rightarrow du = 2xdx \Rightarrow {\Large\frac{du}{2}} = xdx$.
At the lower limit of integration $x = 0 \Rightarrow u = 0^2 = 0$.
At the upper limit of integration $x = 1 \Rightarrow u = 1^2 = 1$.
Hence,
${\huge\int}_{0}^{1} x\,e^{x^2}\,dx = \,{\huge\int}_{u=0}^{u=1}e^u.{\Large\frac{1}{2}}du = {\Large\frac{1}{2}}\,{\huge\int}_{0}^{1}e^u\,du = {\Large\frac{1}{2}}[e^u]_{0}^{1} = {\Large\frac{1}{2}}(e^1 - e^0) = \;$ ${\Large\frac{1}{2}}(e - 1)$.
The process is actually quite tricky until you get the hang of it!
Note: It is essential to draw the region $R$ and from the sketch the limits for the iterated integral, with the order reversed, can be determined.
End of Example 6We illustrate the method with another example.
Example 7
By changing the order of integration evaluate, ${\huge\int}_{0}^{1}\,{\huge\int}_{\sqrt{x}}^{1}\,\sin\,\bigg({\Large\frac{y^3\, +\, 1}{2}}\bigg)\,dy\,dx$.
Solution
As in Example 6, if we tried to evaluate the integral using the current order of integration we would run into difficulties with the integration.
At the moment the region is of Type 1 with vertical scanning lines. We now describe the region $R$ as a Type 2 region by taking horizontal scanning lines.
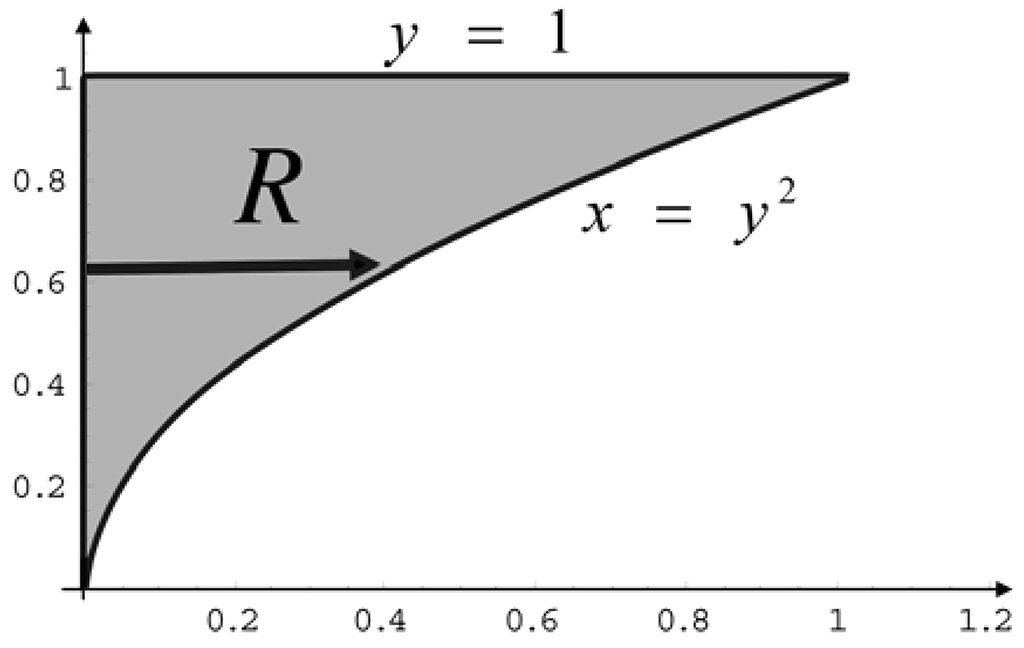
The horizontal scanning line starts at $x = 0$ and finishes on the parabola $x = y^2 \;\,(y = \sqrt{x})$. These horizontal lines are then summed over $R$ from $y = 0$ to $y = 1$ .
Hence, the integral
$$\int_{x = 0}^{x = 1}\,\int_{y = \sqrt{x}}^{y = 1}\,\sin\bigg(\frac{y^3\,+\,1}{2}\bigg)\,dy\,dx$$
on changing the order of integration becomes
$$\int_{y = 0}^{y = 1}\,\int_{x = 0}^{x = y^2}\,\sin\bigg(\frac{y^3\,+\,1}{2}\bigg)\,dx\,dy.$$
Evaluating this integral we have,
Inner integral
${\huge\int}_{x = 0}^{x = y^2}\,\sin\bigg({\Large\frac{y^3\,+\,1}{2}}\bigg)\,dx = \bigg[\,x\,\sin\bigg({\Large\frac{y^3\,+\,1}{2}}\,\bigg)\bigg]_{x = 0}^{x = y^2} = \;$ $y^2\,\sin\bigg({\Large\frac{y^3\,+\,1}{2}}\,\bigg)$.
Outer integral
${\huge\int}_{y = 0}^{y = 1}\,y^2\,\sin\bigg({\Large\frac{y^3\,+\,1}{2}}\,\bigg)\,dy$
Use the substitution,
$u = y^3 + 1 \Rightarrow {\Large\frac{du}{dy}} = 3\,y^2 \Rightarrow du = 3\,y^2\,dy \Rightarrow {\Large\frac{1}{3}}du = y^2\,dy$.
At the lower limit of integration $y = 0 \Rightarrow u = 0^3 + 1 = 1$.
At the upper limit of integration $y = 1 \Rightarrow u = 1^3 + 1 = 2$.
Hence, ${\huge\int}_{y=0}^{y=1}\,y^2\,\sin\bigg(\,{\Large\frac{y^3\, + \, 1}{2}}\,\bigg)\,dy = {\huge\int}_{u=1}^{u=2}\,\sin\bigg({\Large\frac{u}{2}}\bigg).{\Large\frac{1}{3}}du$
$ = {\Large\frac{1}{3}}\,{\huge\int}_{u = 1}^{u = 2}\,\sin\bigg({\Large\frac{u}{2}}\bigg)du$
$= {\Large\frac{1}{3}} \Big[-2\,\cos \Big({\Large\frac{1}{2}}u \,\Big)\,\Big]_{u = 1}^{u = 2} = - {\Large\frac{2}{3}}\Big[\,\cos\Big({\Large\frac{1}{2}}u\,\Big)\,\Big]_{u = 1}^{u = 2}$
$= - {\Large\frac{2}{3}}\bigg(\,\cos(1) - \cos\,\bigg({\Large\frac{1}{2}}\bigg)\bigg)$
$= {\Large\frac{2}{3}}\bigg(\,\cos\bigg({\Large\frac{1}{2}}\bigg) - \,\cos(1)\,\bigg)$.
End of Example 7Now watch the following:
📹 Double Integrals - Changing Order of Integration
📹 Double Integrals: Changing the Order of Integration - Example 1
📹 Double Integrals: Changing the Order of Integration - Example 2
-
6. Double Integration in Polar Coordinates
As we have seen, in order to evaluate a definite integral ${\huge\int}_a^bf(g(x))d\,x$ it is often necessary to use a substitution $u = g(x)$. The integral is then written in terms of $u$ and hopefully the resulting integral becomes easier to integrate.
This idea of changing the variable is now extended to double integrals.
Instead of using Cartesian coordinates $(x,\, y)$ to locate a point $P$ in the plane, we can use polar coordinates $(r,\,\theta)$. The value of $r$ measures the distance from the origin to $P$ and the angle $\theta$ (in radians) locates the position (measured anti-clockwise) relative to the positive direction of the $x$-axis. For example, the point $P$ with polar coordinates $(1,\,\pi / 4)$ , lies on a circle with radius 1 and at an angle of $\pi / 4$ from the $x$ – axis as shown below.
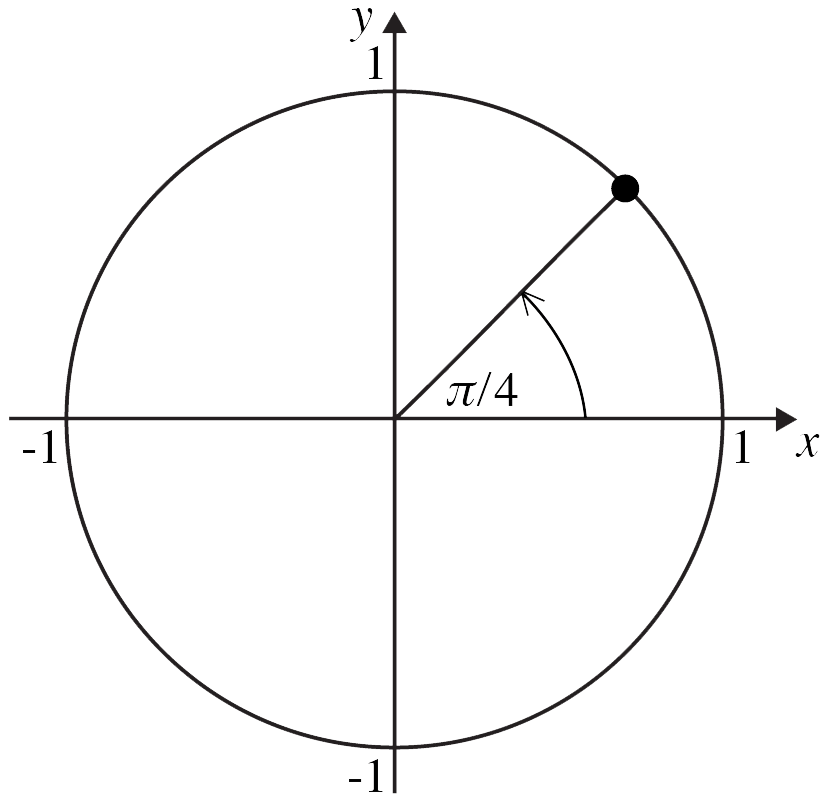
For a general point $P$, the relationship between Cartesian and polar coordinates is given by the equations,
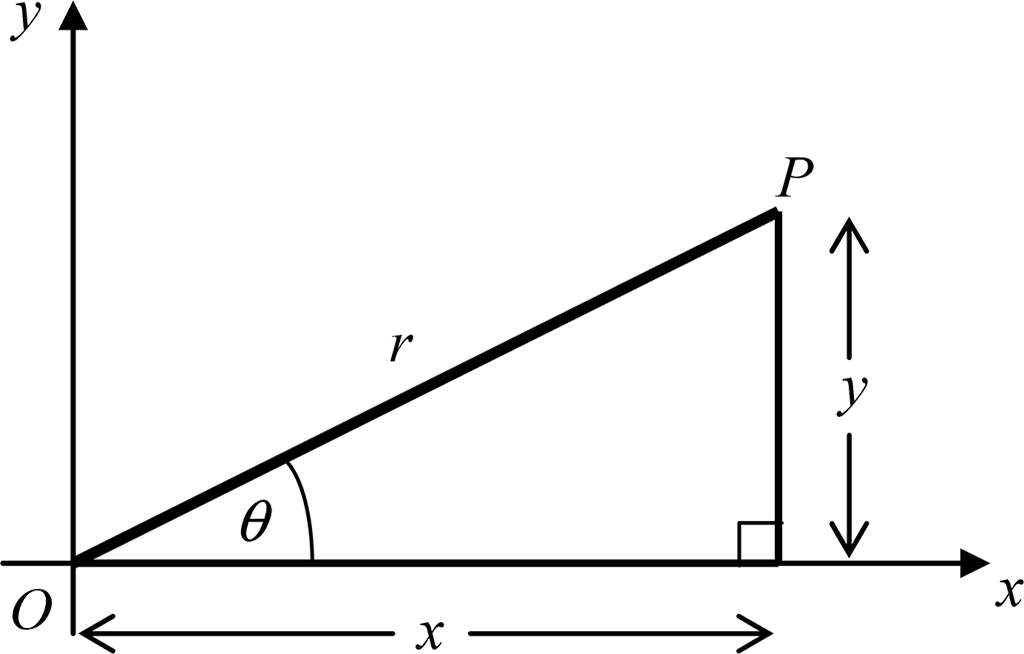
$x = r\,\cos\,\theta$ and $y = r\,\sin\,\theta$.
These equations are obvious from the following diagram using basic trigonometry:
As shown earlier, the double integral ${\Large\iint_{R}} f(x,\,y)dx\,dy$ can be thought of as the volume under the surface $z = f(x,\,y)$ and above the region $R$ in the $xy$ - plane. In Cartesian coordinates the region $R$, was partitioned into small rectangles, $R_{i\,j}$, whose sides, of length $\delta \,x$ and $\delta\,y$, were parallel to the $x$ and $y$ axes respectively. In the construction of the integral, $f(x\,y)$ represents the height of a cuboidal element whose base area is $\delta\,A = \delta\,x\,\delta\,y$ - refer to the diagram in Section 3.
In polar coordinates the plane is partitioned using rays (radial lines) and circles as shown below. Consider a typical element ( $ABCD$ ) which is almost, but not quite, a rectangle. The element is formed by circles of radius $r$ and $r + \delta\,r$ , and rays making angles $\theta$ and $\theta + \delta \,\theta$, with the positive $x$ axis.
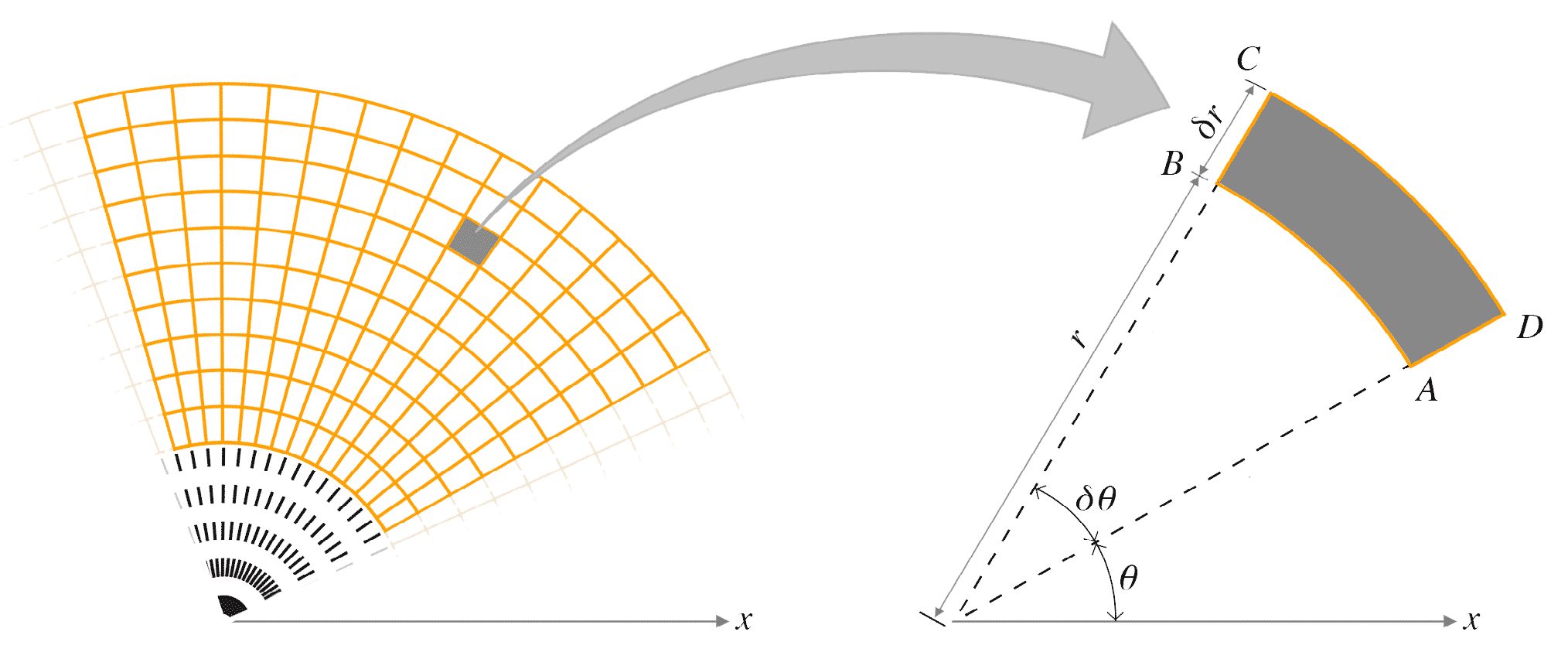
Now assume that our mesh is so small that the arcs $AB$ and $CD$ are approximately equal in length, i.e. of length $r\,\delta\,\theta$. If we consider $ABCD$ as approximately rectangular with sides of length $r\,\delta\,\theta\;$ and $\delta\,r$ its area satisfies $\delta\,A \approx r\,\delta\,r\,\delta\,\theta$. ( In the limit as $\delta\,r$, $\delta\,\theta \rightarrow 0$ we have that $d\,A = r\,d\,r\,d\,\theta$ ). Then
${\large\iint\limits_{R}}f(x,\,y)d\,A \;\;\;\;\;\;= {\Large\iint\limits_{R}} f(x,\,y)dx\,dy$
$$= \overset{{\Large\lim}}{\delta\,r,\,\delta\,\theta \rightarrow 0}\Bigg(\sum_{\text{all}\; R}f(r\,\cos\,\theta, \; r\,\sin\,\theta)r\,d\,r\,d\,\theta\Bigg)$$
$={\Large\iint\limits_{R}} f(r\,\cos\,\theta, \; r\,\sin\,\theta)r\,d\,r\,d\,\theta$.
NOTE: $dx\, dy$ changes to $r\,d\,r\,d\,\theta$ in polar coordinates.
A double integral is often easier to evaluate by changing to polar coordinates when the region $R$ is circular or segments of a circle
Now watch the following up to 3:32:
📹 Introduction to Double Integrals in Polar Coordinates
Example 8
Determine the volume of the solid bounded by $z = \sqrt{a^2 - x^2 - y^2}$ and the plane $z = 0$.
Solution
Firstly observe that $z = + \sqrt{a^2 - x^2 - y^2}$ represents an upper hemisphere of radius $a$. Hence, the region $R$ is a circle of radius $a$ in the $xy$ ‒ plane, shaded in the figure below.
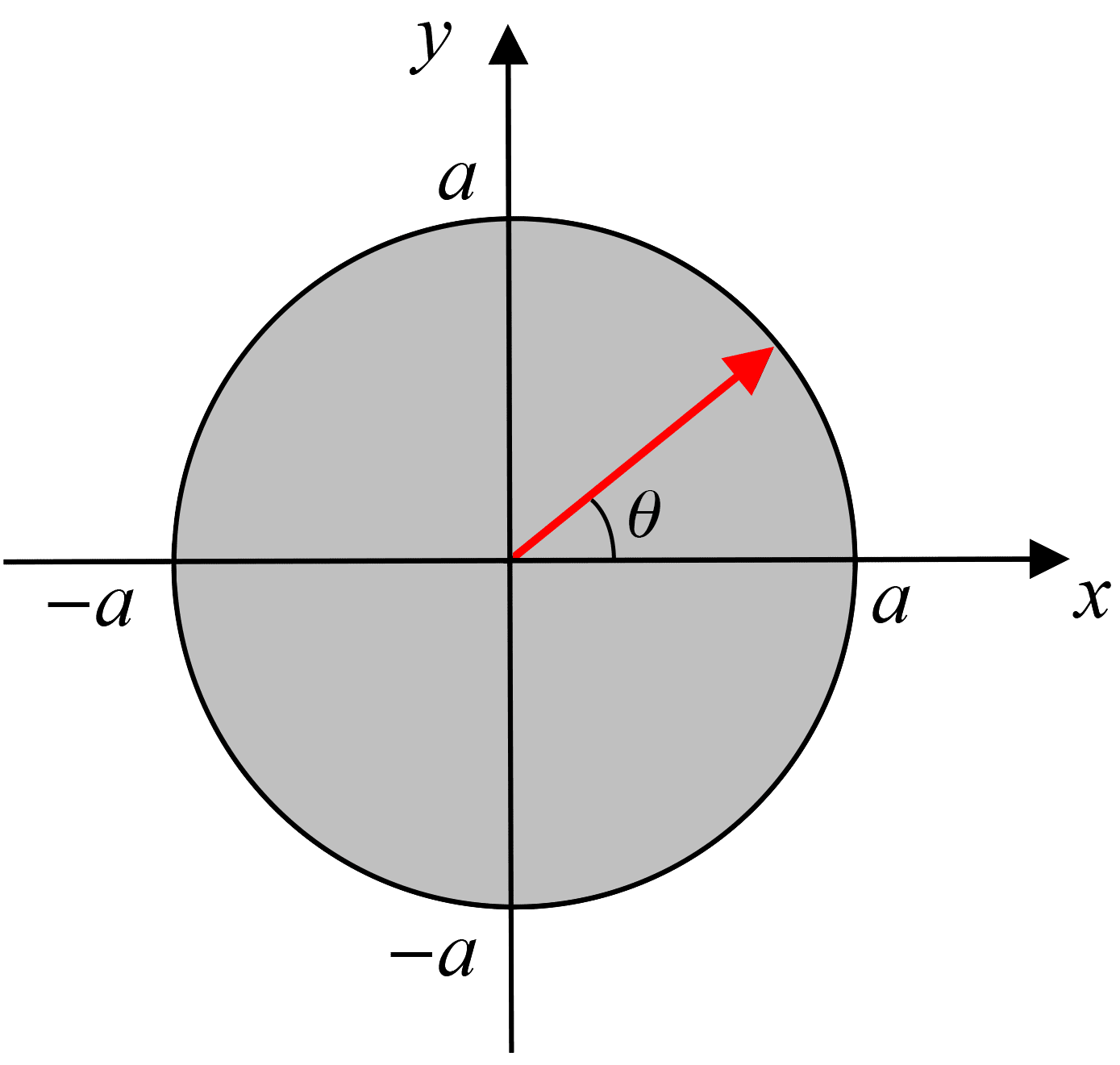
The volume of the upper hemisphere is given by,
$V = {\Large\iint\limits_{R}}\sqrt{a^2 - x^2 - y^2}\;dx\,dy$.
$= {\Large\iint\limits_{R}}\sqrt{a^2 - (x^2 + y^2)}\;dx\,dy, \;R = \{(x\,y) : x^2 + y^2 \le a^2\}$.
In polar coordinates, $x^2 + y^2 = r^2$ and $dx\,dy$ changes to $r\,d\,r\,d\,\theta$ , so
$V = {\Large\iint\limits_{R}}\sqrt{a^2 - r^2}\;r\,d\,r\,d\,\theta$.
We now determine the limits of integration.
In polar coordinates we integrate along the radial direction first ( regarding $\theta$ as constant ) and then sweep out the region $R$ by varying $\theta$.
Here the radial scanning line starts at $r = 0$ and finishes at $r = a$. The full circle is swept out by varying $\theta$ from $\theta = 0$ to $\theta = 2\,\pi$.
Hence,
$V = {\huge\int}_{\theta = 0}^{\theta = 2\,\pi} {\huge\int}_{r = 0}^{r = a} \sqrt{a^2 - r^2}\;r\,d\,r\,d\,\theta$.
Inner integral
${\huge\int}_{r = 0}^{r = a}\sqrt{a^2 - r^2}\;r\,d\,r$.
Use integration by substitution.
Let $u = a^2 - r^2$ so that $du = - 2\,r\,d\,r$ or $- {\Large\frac{1}{2}}du = r\,d\,r$ .
At the lower limit of integration $r = 0 \Rightarrow u = a^2$.
At the upper limit of integration $r = a \Rightarrow u = 0$.
Hence, ${\huge\int}_{r = 0}^{r = a} \sqrt{a^2 - r^2}\;r\,d\,r = -{\Large\frac{1}{2}} {\huge\int}_{u = a^2}^{u = 0}\;u^{1/2}d\,u$
$= -{\Large\frac{1}{2}}\bigg[{\large\frac{2}{3}}u^{3/2}\bigg]_{u = a^2}^{u = 0} = -{\Large\frac{1}{3}}\Big[u^{3/2}\Big]_{a^2}^{0} = - {\Large\frac{1}{3}}\Big[(0)^{3/2} - (a^2)^{3/2}\Big] =\;$ ${\Large\frac{1}{3}}a^3$.
Outer integral
$V = {\huge\int}_{\theta = 0}^{\theta = 2\,\pi} {\Large\frac{1}{3}}a^3d\,\theta = {\Large\frac{1}{3}}a^3 {\huge\int}_{\theta = 0}^{\theta = 2\,\pi} 1\,d\,\theta = {\Large\frac{1}{3}}a^3\big[\theta\big]_{0}^{2\,\pi} = \;$ ${\Large\frac{2\,\pi\,a^3}{3}}$.
NOTE: It is straightforward to check our answer as the volume of a sphere of radius $a$ is ${\Large\frac{4\,\pi\,a^3}{3}}$ and so the hemisphere’s area will be half this value, which is the answer we obtained.
Now watch the following:
📹 Double Integrals in Polar Coordinates – Example 1
End of Example 8Example 9
Consider the double integral,
${\huge\int}_{-2}^{\,\,2}{\huge\int}_{0}^{f(x)}x \sqrt{x^2 + y^2}\,dy\,dx$ where $f(x) = \sqrt{4 - x^2}$.
(i). Sketch the region of integration.
(ii). Express the integral in terms of polar coordinates $r$ and $\theta$.
(iii). Using your answer to part (ii) evaluate the double integral.
Solution
(i). From the limits given in the integral we have that,
$x$ ranges from $x = - 2$ to $x = 2$
$y$ ranges from $y = 0$ to $y = \sqrt{4 - x^2}$.
Now, $y = +\, \sqrt{4 - x^2}$ represents the upper half of a circle of radius, $r = 2$ as shown in the diagram below.

(ii). $x = r\,\cos\,\theta\;\;$, $y = r\,\sin\,\theta\;\;$, $x^2 + y^2 = r^2\;\;$, $dy\,dx \rightarrow r\;dr\;d\theta$.
The radial scanning line, shown in red, starts at $r = 0$ and finishes at $r = 2$.
The region $R$ is swept out by varying $\theta$ from $\theta = 0$ to $\theta = \pi$.
Expressing the integral in polar coordinates we have,
$I = {\huge\int}_{-2}^{\,\,2} {\huge\int}_{0}^{f(x)}\,x \,\sqrt{x^2 + y^2}\,dy\,dx$ where $f(x) = \sqrt{4 - x^2}$
$= {\huge\int}_{0}^{\pi} {\huge\int}_{0}^{2}\, r\,\cos\,\theta.\sqrt{r^2}.r\,dr\,d\theta$
$= {\huge\int}_{0}^{\pi} {\huge\int}_{0}^{2}\,r^3\,\cos\theta\,dr\,d\theta$.
(iii). Evaluating the integral,
Inner integral
${\huge\int}_{0}^{2}\,r^3\cos\theta\,dr\;\;\;\; = \bigg[{\Large\frac{r^4}{4}}\cos\theta\bigg]_{r = 0}^{r = 2} = 4 \cos\theta - 0 \;\; = \;$ $4 \cos \theta$.
Outer integral
$4{\huge\int}_{0}^{\pi}\cos\theta\,d\theta = 4\Big[\sin(\theta)\Big]_{0}^{\pi} = 4\Big[\sin(\pi) - \sin(0)\Big]$
$= 4\Big[0 - 0\Big] = \;$ $0$.
Now watch the following:
📹 Double Integrals in Polar Coordinates – Example 2
End of Example 9Example 10
By converting to polar coordinates, evaluate ${\large\iint\limits_{R}}\,y\,dx\,dy$ where $R$ is the region in the first quadrant that lies between the circles $x^2 + y^2 = 4$ and $x^2 + y^2 = 2x$.
Solution
The equation $x^2 + y^2 = 4$ represents a circle of radius 2 centred on the origin .The equation $x^2 + y^2 - 2x = 0$ can be written as $(x - 1)^2 + y^2 = 1^2$ and so represents a circle of radius 1, centred at the point $(1,\,0)$.
The region $R$ is the region shown shaded below.
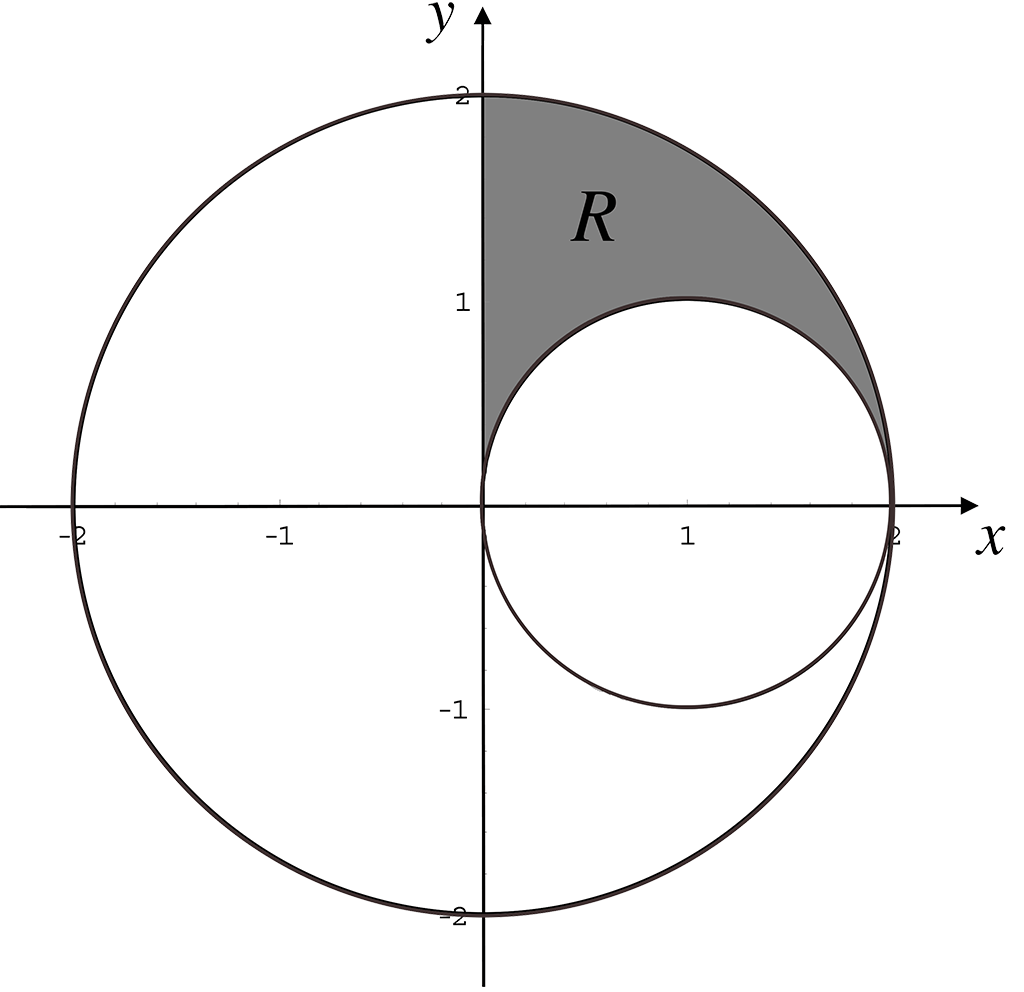
In polar coordinates ${\Large\iint\limits_{R}}\,y\,dx\,dy$ becomes ${\Large\iint\limits_{R}}\,r\sin\theta.r\,dr\,d\theta = {\Large\iint\limits_{R}}\,r^2\sin\theta\,dr\,d\theta$.
The circle $x^2 + y^2 = 4$ has polar equation $r^2 = 4 \Rightarrow r = 2$ ( since $r$ is positive ).
The circle $x^2 + y^2 = 2x$ has polar equation $r^2 = 2\,r\,\cos\theta$ or $r = 2\,\cos\theta$.
The figure below zooms in on the first quadrant in the above diagram. Integrate first along the radial direction at a fixed value of $\theta$ as shown below. The radial scanning line starts at $r = 2\cos\theta$ and finishes at $r = 2$. The region $R$ is swept out by varying $\theta$ from $\theta = 0$ to $\theta = {\Large\frac{\pi}{2}}$.
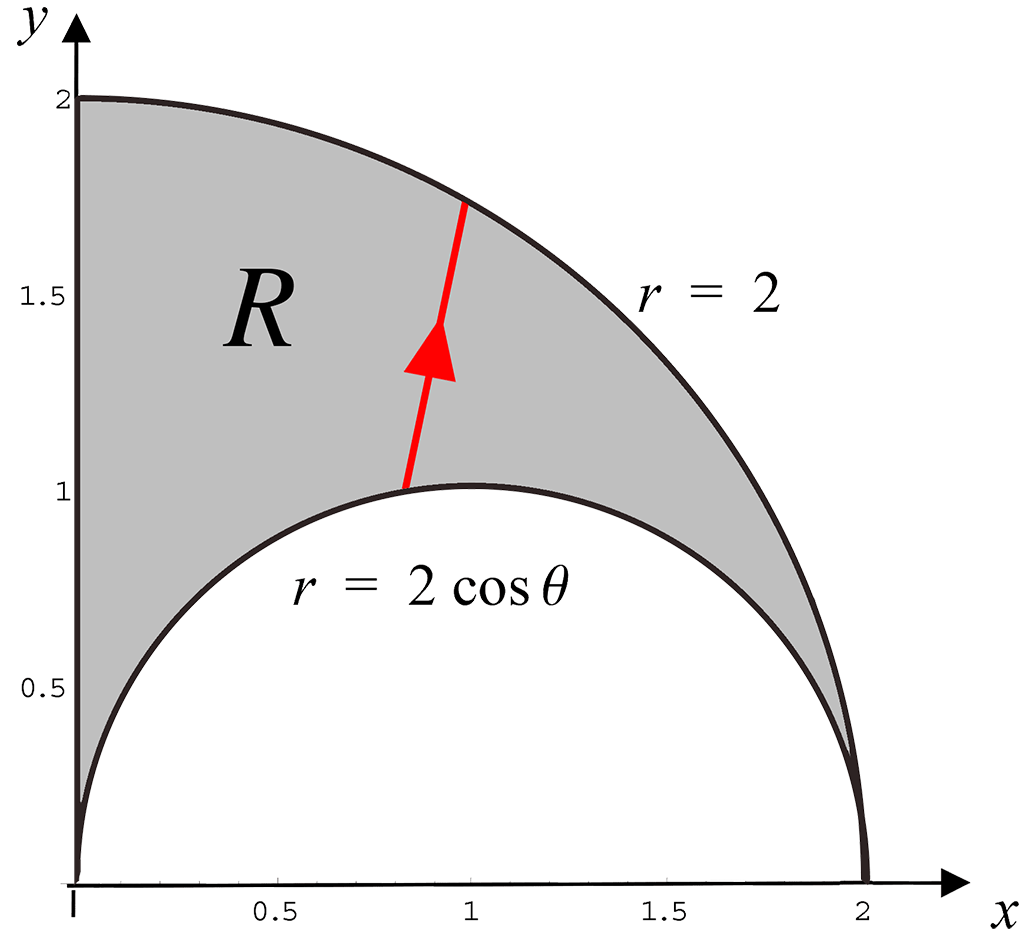
Hence, ${\Large\iint\limits_{R}}\,r^2\sin\theta\,dr\,d\theta = {\Large\int}_{\theta = 0}^{\theta = \pi/2}{\Large\int}_{r = 2\cos\theta\;}^{r = 2}\,r^2\sin\theta\,dr\,d\theta$.
Inner integral
${\huge\int}_{r = 2\cos\theta\;}^{r = 2}r^2\sin\theta\,dr$ ( regard $\theta$ as a constant )
$= \bigg[{\Large\frac{1}{3}}r^3\sin\theta\bigg]_{r = 2\cos\theta}^{r = 2} = {\Large\frac{8}{3}}\sin\theta - {\Large\frac{8}{3}}\cos^3\theta\sin\theta = \;$ ${\Large\frac{8}{3}}(\sin\theta - \cos^3\theta\sin\theta)$.
Outer integral
${\Large\frac{8}{3}}{\huge\int}_{\theta = 0}^{\theta = \pi/2}(\sin\theta - \cos^3\theta\sin\theta)\,d\theta$
$= {\Large\frac{8}{3}}\bigg[-\cos\theta + {\Large\frac{1}{4}}\cos^4\theta\bigg]_{0}^{\pi/2}$ (see Note 1 below)
$= {\Large\frac{8}{3}}\bigg(-\cos\bigg({\Large\frac{\pi}{2}}\bigg) + {\Large\frac{1}{4}}\cos^4\bigg({\Large\frac{\pi}{2}}\bigg)\bigg) - {\Large\frac{8}{3}}\bigg(-\cos(0) + {\Large\frac{1}{4}}\cos^4(0)\bigg)$
$= {\Large\frac{8}{3}}(0 + 0) - {\Large\frac{8}{3}}\bigg(-1 + {\Large\frac{1}{4}}\bigg)$
$= {\Large\frac{8}{3}} - {\Large\frac{2}{3}} = \;$ $2$ .
NOTES
1. $\;\;\;{\huge\int}_{\theta = 0}^{\theta = \pi/2}\cos^3\theta\sin\theta\,d\theta\;$ can be evaluated by using the substitution, $u = \cos(\theta)$.
2. We could have used Cartesian coordinates to evaluate ${\Large\iint\limits_{R}}\;y\,dy\,dx$.
Taking a vertical scanning line
${\Large\iint\limits_{R}}\,y\,dy\,dx = {\Large\int}_{x = 0}^{x = 2}{\Large\int}_{y = \sqrt{2x - x^2}}^{y = \sqrt{4 - x^2}}\;y\,d\,y\,d\,x$.
We leave you to show that this will give an answer of 2 as obtained above using polar coordinates.
End of Example 10 -
7. Applications (NON-EXAMINABLE)
(a). Pressure Distributions
Consider a pressure distribution acting on some planar surface of finite dimensions. Pressure is defined as Force per unit area. If pressure is constant over the whole surface then
Total Force = Pressure × Area of surface .
If the pressure varies from point to point on the surface then we can use a double integral to calculate the total force.
Suppose the surface is represented by a region $R$ in the $Oxy$ plane as shown below.

Denote the pressure distribution by $p(x,y)$. The force acting on a small rectangle at $(x_i, \,y_j)$ is approximately $p(x_i,\,y_j)\delta y\,\delta x$.
Therefore the total force over all $R$ is approximately $\hat{F} = {\large\sum\limits_{i=1}^{n}}\;{\large\sum\limits_{j=1}^{m(i)}}\,p(x_i,\,y_j)\,\delta y\,\delta\,x$ and exactly $F = {\Large\iint\limits_{R}}\,p(x,\,y)\,dy\,dx$.
(b). Density Distributions
A prismatic solid is one with a uniform cross-section, such as the shape $R$ shown below. For certain purposes we may regard such solids as two-dimensional. We can, without loss of generality, assume the third dimension to have length 1 (i.e the height of the solid is 1 unit)

The above diagram represents the view from above of a 2-dimensional prismatic solid.
Density is defined as Mass per unit Volume. If the density distribution is constant, say $\rho_0$, then Total Mass = $\rho_0 \times$ Volume.
In a prismatic solid, suppose density varies with position over the cross-section; denote this by $\rho(x,\,y)$.
For a small cuboid through the solid defined by a small rectangle on the cross-section at $(x_i,\,y_j)$, the volume is $1\,\delta\,y\,\delta\,x = \delta\,y\,\delta\,x$.
The mass of that cuboid is approximately $\rho(x_i,\,y_j)\delta\,y\,\delta\,x$ and so the total mass is approximately $\hat{M} = {\large\sum\limits_{i=1}^{n}}\,{\large\sum\limits_{j=1}^{m(i)}}\,\rho(x_i,\,y_j)\,\delta\,y\,\delta\,x$ and exactly $M = {\Large\iint\limits_{R}}\,\rho(x,\,y)\,dy\,dx$.
(c). Centre of Mass of a 2-Dimensional Prismatic Solid

The above diagram represents the view from above of a 2-dimensional prismatic solid with a density distribution denoted by $\rho(x,\,y)$. The 2-dimensional solid has a centre of mass at $C$, the point of balance of the solid.
The mass of a typical volume element is given by $\rho(x_i,\,y_j)\,\delta\,y\,\delta\,x$.
The distance of the element from the line $x = \bar{x}$ is $(x_i - \bar{x})$.
The distance of the element from the line $y = \bar{y}$ is $(y_j - \bar{y})$.
For $C$ to be the centre of mass (point of balance) we require
${\large\sum\limits_{i}}\,{\large\sum\limits_{j}}(x_i - \bar{x})\,\rho(x_i,\,y_j)\,\delta\,y\,\delta\,x = 0$
and
${\large\sum\limits_{i}}\,{\large\sum\limits_{j}}(y_j - \bar{y})\,\rho(x_i,\,y_j)\,\delta\,y\,\delta\,x = 0$.
Letting $\delta\,x$ and $\delta\,y$ tend to zero we obtain the balance conditions
${\Large\iint\limits_{R}}(x - \bar{x})\,\rho(x,\,y)\,dy\,dx = 0$
and
${\Large\iint\limits_{R}}(y - \bar{y})\,\rho(x,\,y)\,dy\,dx = 0$.
Since $\bar{x}$ and $\bar{y}$ are constants, these equations can be rearranged to give formulae for the coordinates of the centre of mass:
$\bar{x} = {\Large\frac{\iint\limits_{R}\,x\,\rho(x,\,y)\,dy\,dx}{\iint\limits_{R}\,\rho(x,\,y)\,dy\,dx}} = {\Large\frac{I_x}{M}}$
and
$\bar{y} = {\Large\frac{\iint\limits_{R}\,y\,\rho(x,\,y)\,dy\,dx}{\iint\limits_{R}\,\rho(x,\,y)\,dy\,dx}} = {\Large\frac{I_y}{M}}$
where $M$ is the total mass of the solid.
(d). Moment of Inertia of a Prismatic Solid
The moment of inertia of a prismatic solid about a point $(x_0,\,y_0)$ is defined to be
$I = {\Large\iint\limits_{R}}\Big((x - x_0)^2 + (y - y_0)^2\Big)\rho(x,\,y)\,dy\,dx$
where $\rho(x,\,y)$ is the density distribution function for the solid.
If the density is uniform (i.e constant, say $\rho_0$ ) and the moment of inertia is taken about the origin, then
$I = {\Large\iint\limits_{R}}(x^2 + y^2)\,\rho_0\,dy\,dx = \rho_0\,{\Large\iint\limits_{R}}(x^2 + y^2)\,dy\,dx$
-
Summary
- In this unit we have extended the concept of the definite integral of a function of a single variable to double integrals involving functions of two variables. You should now be able to:
- understand the application of double integration to computing volumes.
- evaluate a double integral over a rectangular region in the $xy$ – plane by writing it as an iterated integral.
- evaluate double integrals over general regions in the $xy$ – plane.
- identify when it is advantageous to change (reverse) the order of integration. Determine and evaluate the resulting integral.
- convert double integrals from Cartesian to polar coordinates.
The next unit introduces Laplace transforms and describes their application to solving ordinary differential equations which are either very difficult, or even impossible, to solve using the methods we have previously encountered.