-
1. Introduction
The idea of transforming a “difficult” problem into an “easier” problem is one that is used widely in mathematics. Diagrammatically we have
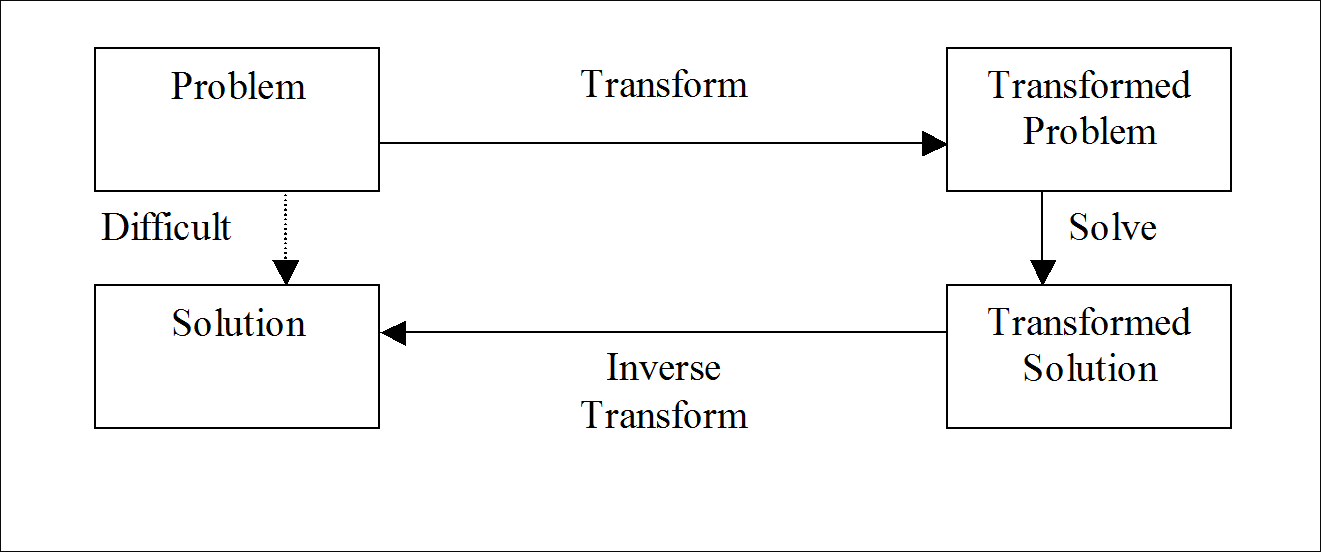
There are many types of transforms available to mathematicians, engineers and scientists. In this unit we are going to examine one such transformation, the Laplace transform, which can be used to solve certain types of differential equations and also has applications in control theory.
-
2. Definition
The Laplace transform (LT) is an integral transform that operates on functions of $t$, where $t$ is often taken to represent time. Given a function $f(t)$ its Laplace transform is defined as
$$\mathscr{L}\,\{f(t)\} = \int_{0}^{\infty}\,f(t)\,e^{-s t}\,dt$$
where $s$ is called the Laplace variable. Alternative notation for the Laplace transform includes
$\mathscr{L}\,\{f(t)\} = F(s)$ or $\mathscr{L}\,\{f(t)\} = \bar{f}(s)$.
Laplace transforms are usually only concerned with functions where $t \ge 0$.
When applying the Laplace transform a function of the real variable, $t$, is transformed to a function of the complex variable, $s$. Because the function of $t$ is often some form of time signal, we often talk about moving from the time $( t )$ domain to the Laplace $( s )$ domain when we perform a Laplace transformation.
Now watch the following:
📹 Introduction to Laplace Transforms
Example 1
Determine the Laplace transform of $f(t) = 1$ using the definition.
$$\mathscr{L}\,\{1\}\;\;\; = \int_{0}^{\infty}1.e^{-s t}\,dt$$
$$= \overset{{\large\lim\;}}{{\small u} {\small\rightarrow \infty}} \int_{0}^{u}e^{-s t}\,dt$$
$$= \overset{{\large\lim\;}}{{\small u} {\small\rightarrow \infty}} \bigg[-\frac{1}{s}e^{-s t}\bigg]_{t=0}^{t=u}$$
$$= - \frac{1}{s}\; \overset{{\large\lim\;}}{{\small u} {\small\rightarrow \infty}}\;(e^{-s u} - e^0)$$
$= - {\Large\frac{1}{s}}\;(0 - 1) $ ( provided $s > 0$ )
$$= \frac{1}{s}.$$
Now watch the following:
📹 Calculating Laplace Transforms from the Definition
End of Example 1Example 2
Determine the Laplace transform of, $f(t) = t$.
$$\mathscr{L}\{t\} = \int_{0}^{\infty}\;t.e^{-s t}\,dt$$
To evaluate this integral requires integration by parts and it can readily be shown that, provided $s > 0$,
$$\mathscr{L} \{t\} = \frac{1}{s^2}.$$
Very quickly the integrations required to complete the Laplace transformation become difficult and messy. For this reason, we generally work from a table of pre-determined Laplace transforms (see Appendix).
End of Example 2Using the Table of Laplace Transforms
We illustrate the procedure with some examples:
Example 3
(i). Determine $\mathscr{L}\{t^3\}$.
Now, $t^3$ is not in the table explicitly, but $t^n$ is:
$\mathscr{L}\{t^n\} = {\Large\frac{n!}{s^{n+1}}}$ (#4 in the table)
For $t^3$ we require $n = 3$:
Hence, $\mathscr{L}\{t^3\}\;$ $= {\Large\frac{3!}{s^4}} = {\Large\frac{3 \times 2 \times 1}{s^4}} = {\Large\frac{6}{s^4}}$.
(ii). Determine $\mathscr{L}\{e^{-2t}\}$.
From # 5 in the table:
$\mathscr{L} \{e^{-\alpha t}\} = {\Large\frac{1}{s + \alpha}}$.
Set $\alpha = 2$ to obtain:
$\mathscr{L} \{e^{-2 t}\} =\;$ ${\Large\frac{1}{s + 2}}$.
(iii). Determine $\mathscr{L}\;\{\sin(4t)\}$.
From # 8 in the table:
$\mathscr{L}\;\{\sin(4t)\} = {\Large\frac{\omega}{s^2 + \omega^2}}$.
Set $\omega = 4$ to obtain :
$\mathscr{L} \{\sin(4t)\}\;$ $= {\Large\frac{4}{s^2 + 4^2}} = {\Large\frac{4}{s^2 + 16}}$.
End of Example 3 -
3. Properties of the Laplace Transform
The Laplace transform has several special properties that make it a useful mathematical tool.
(a). Linearity
Suppose we have two functions along with their respective Laplace transforms:
$\mathscr{L} \{f(t)\} = F(s)$ and $\mathscr{L} \{g(t)\} = G(s)$
The linearity property means that
$\mathscr{L} \{af(t) + bg(t)\} = aF(s) + bG(s)$
providing $a$ and $b$ are constants. This makes the transformation of a string of functions straightforward.
Example 4
$\mathscr{L}\{2\cos(\omega t) + 3\sin(\omega t)\} = 2{\Large\frac{s}{s^2 + \omega^2}} + 3{\Large\frac{\omega}{s^2 + \omega^2}} = \;$ ${\Large\frac{2s + 3 \omega}{s^2 + \omega^2}}$.
End of Example 4WARNING: The Laplace transform of a product is NOT EQUAL TO the product of the individual Laplace transforms, i.e.
$\mathscr{L}\; \{f(t)g(t)\}\;\; \neq\;\; \mathscr{L}\; \{f(t)\} \;\;\mathscr{L}\; \{g(t)\}$.
We have to invoke other properties of the Laplace transform to deal with products.
(b). The First Shifting Theorem
Suppose a function $f(t)$ has the Laplace transform $F(s)$. It is easily demonstrated that
$\mathscr{L}\;\{e^{-\alpha t}f(t)\} = F(s + \alpha)$.
Now watch the following:
Example 5
Determine $\mathscr{L}\,\{e^{-2t}t^3\}$.
From tables and Example (3)(i) we have
$\mathscr{L}\;\{t^3\} = {\Large\frac{6}{s^4}}$. $[1]$
Then, by the first shifting property with $\alpha = 2$ we have that
$\mathscr{L}\;\{e^{-2 t}t^3\} = \;$ ${\Large\frac{6}{(s + 2)^4}}$.$[2]$
Note that to obtain $[2]$ from $[1]$ we merely replace $s$ by $(s + 2)$.
End of Example 5(c). Transformation of Derivatives
As before, denote the Laplace transform of $f(t)$ by $F(s)$. Now consider the Laplace transform of the derivative of $f(t)$, denoted by $\dot{f}(t)$. From the definition we have:
$$\mathscr{L}\;\{\dot{f}(t)\} = \int_{0}^{\infty}\dot{f}(t)e^{- s t}\,dt.$$
Using integration by parts, where we integrate $\dot{f}(t)$ and differentiate $e^{- s t}$, gives
$$\mathscr{L}\;\{\dot{f}(t)\} = \int_{0}^{\infty} \dot{f}(t)e^{- s t}\, dt$$
$$= \bigg[ f(t)e^{- s t}\bigg]_{0}^{\infty} - \int_{0}^{\infty} f(t)(-s)e^{- s t}\,dt $$
$$= 0 - f(0) + s \int_{0}^{\infty} f(t)e^{- s t}\, dt$$
$$= -f(0) + sF(s).$$
Hence,
$$\mathscr{L}\;\{\dot{f}(t)\} = sF(s) - f(0).$$
We have expressed the Laplace transform of a derivative in terms of the Laplace transform of the undifferentiated function. In effect, the Laplace transform has converted the operation of differentiation into the simpler operation of multiplication by $s$ .
In a similar fashion, using repeated integration by parts, we can show that
$$\mathscr{L}\;\{\ddot{f}(t)\} = s^2F(s) - sf(0) - \dot{f}(0).$$
This result is one of the most important properties of the Laplace transform. The Laplace transform “gets rid of” derivatives; just the thing for solving differential equations!
When we come to solve differential equations using Laplace transforms we shall use the following alternative notation:
$$\mathscr{L}\;\{x\} = \bar{x}.$$
$$\mathscr{L}\;\{\dot{x}\} = s\bar{x} - x(0)$$
$$\mathscr{L}\;\{\ddot{x}\} = s^2\bar{x} - sx(0) - \dot{x}(0).$$
However, before we can solve differential equations we need to look at the reverse process of finding functions of $t$ from given Laplace transforms.
-
4. Inverse Laplace Transforms
So far, we have looked at how to determine the LT of a function of $t$ , ending up with a function of $s$ . The table of LTs collects together the results we have considered, and more. When we apply LTs to solve problems we need to invoke the inverse transformation. That is, given a Laplace transform, $F(s)$, we need to determine the corresponding function, $f(t)$. In general we have
$$\mathscr{L}^{-1}\;\{F(s)\} = \frac{1}{2\pi j} \int_{\gamma \,-\, j\, \infty}^{\gamma \,+\, j \,\infty}F(s)e^{st}\,ds$$
where evaluation of the integral requires a knowledge of complex analysis and will not be considered here. Instead, we shall rely on the table of LTs used in reverse to provide inverse LTs. This procedure will involve manipulating a given Laplace transform until it ‘looks like’ one or more entries in the $F(s)$ column of the table. The inverse LT is then determined from the corresponding $f(t)$ column in the table. The following examples illustrate the main algebraic techniques required. These include completing the square, factorisation and the formation of partial fractions.
Example 6
Invert the Laplace transform, ${\Large\frac{3}{s^6}}$.
The closest entry in the table is #4 which gives
$$\mathscr{L}^{-1} \bigg\{\frac{n!}{s^{n+1}}\bigg\} = t^n.$$
Setting $n = 5$ we have
$$\mathscr{L}^{-1}\bigg\{\frac{5!}{s^6}\bigg\} = \mathscr{L}^{-1} \bigg\{ \frac{120}{s^6}\bigg\} = t^5.$$
In the given Laplace transform there is a 3 in the numerator and so we must manipulate the expression obtained from the tables which has 120 in the numerator. To do so we multiply by the value we want in the numerator (3) and divide by the value introduced from the tables (120). We then have
$$\frac{3}{s^6} = \frac{3}{120} \frac{120}{s^6} = \frac{1}{40}\bigg[\frac{120}{s^6}\bigg].$$
The term in the square brackets is now exactly the table entry so we can invert that and simply multiply by the fraction in front:
$\mathscr{L}^{-1}\bigg\{{\Large\frac{3}{s^6}}\bigg\} = \;$ ${\Large\frac{1}{40}}t^5$.
End of Example 6Example 7
Invert the Laplace transform, ${\Large\frac{1}{s^2\, +\, 2s \,+\, 5}}$.
This example requires the technique known as “completing the square” and a little bit of fine tuning to rewrite it in a form that can be inverted directly from the table. Note that the closest entry in the table is #14 giving:
$$\mathscr{L}^{-1}\bigg\{\frac{\omega}{(s + \alpha)^2 + \omega^2}\bigg\} = e^{- \alpha t}\sin(\omega\,t).$$
Now complete the square in the denominator:
$$s^2 + 2s + 5 = (s + 1)^2 - 1 + 5 = (s + 1)^2 + 4.$$
The given transform becomes:
$$\frac{1}{s^2 + 2s + 5} = \frac{1}{(s + 1)^2 + 4} = \frac{1}{(s + 1)^2 + 2^2}\;.$$
This expression is now very close to the table entry with $\alpha = 1$ and $\omega = 2$. We would like there to be a 2 in the numerator so “fine tuning” gives
$$\frac{1}{(s + 1)^2 + 2^2} = \frac{1}{2}\bigg[\frac{2}{(s + 1)^2 + 2^2}\Bigg] ,$$
where the term in the square brackets is exactly the table entry with $\alpha = 1$ and $\omega = 2$.
Inverting this expression and multiplying by the fraction gives
${\Large\frac{1}{2}} \mathscr{L}^{-1}\bigg\{{\Large\frac{2}{(s + 1)^2 + 2^2}}\bigg\} = \;$ ${\Large\frac{1}{2}}e^{- t}\sin(2t)$.
End of Example 7Example 8
(i). Detemine $\mathscr{L}^{-1}\bigg\{{\Large\frac{s\, +\, 5}{s^2 \,-\, 2s \,-\, 3}}\bigg\}$ using partial fractions.
Factorise the denominator and obtain the partial fraction representation of the resulting expression. Note that the details of the partial fraction expansion have been omitted.
$$\frac{s + 5}{s^2 - 2s - 3} = \frac{s + 5}{(s - 3)(s + 1)} = \frac{2}{s - 3} - \frac{1}{s + 1}.$$
Examination of the tables shows that # 5 is the appropriate choice giving
$$\mathscr{L}^{-1}\bigg\{\frac{1}{s + \alpha}\bigg\} = e^{- \alpha t}.$$
Using this result with $\alpha = - 3$ and $\alpha = + 1$ gives
$\mathscr{L}^{-1} \bigg\{{\Large\frac{2}{s - 3}}\bigg\} - \mathscr{L}^{-1}\bigg\{{\Large\frac{1}{s + 1}}\bigg\} = \;$ $2e^{3t} - e^{-t}$
(ii). Detemine $\mathscr{L}^{-1}\bigg\{{\Large\frac{s \,+\, 5}{s^2 \,-\, 2s \,-\, 3}}\bigg\}$ by completing the square.
If we fail to notice that the denominator can be factorised, then completing the square is still an option:
$$\frac{s + 5}{s^2 - 2s - 3} = \frac{s + 5}{(s - 1)^2 - 1 - 3} = \frac{s + 5}{(s - 1)^2 - 4} = \frac{s + 5}{(s - 1)^2 - 2^2} \;.$$
The minus sign in the denominator is significant since it no longer conforms to the form
$$(s + \alpha)^2 + \omega^2.$$
we had in Example 7.
Instead we need the following results, # 19 and #21 in the tables, i.e.
$$\mathscr{L}^{-1}\{e^{- \alpha t}\sinh \,(\beta t)\} = \frac{\beta}{(s + \alpha)^2 - \beta^2}$$
$$\mathscr{L}^{-1}\{e^{- \alpha t} \cosh\,(\beta t)\} = \frac{s + \alpha}{(s + \alpha)^2 - \beta^2} $$
where sinh (pronounced “shine”) and cosh (pronounced “cosh”) are the so-called hyperbolic functions. Fine tuning the Laplace transform a little bit more gives
$$\frac{s + 5}{(s - 1)^2 - 2^2} = \frac{(s - 1) + 6}{(s - 1)^2 - 2^2} = \bigg[\frac{(s - 1)}{(s - 1)^2 - 2^2}\bigg] + 3\bigg[\frac{2}{(s - 1)^2 - 2^2}\bigg].$$
Inverting the terms in square brackets using # 19 and #21 in the tables gives,
$$\mathscr{L}^{-1} \bigg\{\frac{s + 5}{s^2 - 2s - 3}\bigg\} = \mathscr{L}^{-1} \bigg\{\frac{(s - 1)}{(s - 1)^2 - 2^2}\bigg\} + 3\; \mathscr{L}^{-1}\bigg\{\frac{2}{(s - 1)^2 - 2^2}\bigg\}$$
$$= e^t \cosh(2t) + 3e^t \sinh(2t)$$
$$= e^t [\cosh(2t) + 3 \sinh(2t)].$$
Note: By applying the following mathematical identities:
$\cosh\,(\beta t) = {\Large\frac{1}{2}}[e^{+ \beta t} + e^{- \beta t}]$ and $\sinh\,(\beta t) = {\Large\frac{1}{2}}[e^{+ \beta t} - e^{- \beta t}]$
we can easily show that the two versions of the answer, in parts (i) and (ii), are equivalent.
End of Example 8Now watch the following:
📹 Find Basic Inverse Laplace Transforms
📹 Find Inverse Laplace Transforms: $\sin(at)$ and $\cos(at)$
📹 Find the Inverse Laplace Transform of $Y(s)$ - Example
📹 Find the Inverse Laplace Transform of $Y(s)$ Using Partial Fractions - Example
📹 Find Inverse Laplace Transforms: $\sinh(at)$ and $e^{(at)}$
-
5. Using Laplace Transforms to Solve ODEs
- We have seen how the Laplace transform of the derivative of a function can be expressed in terms of the Laplace transform of the undifferentiated function. We can use this property to derive solutions to certain types of differential equations. The process is broken down into the following steps:
- Transform both sides of the ODE;
- Substitute initial values;
- Solve for $\bar{x}$;
- Manipulate into a form that can be inverted from tables;
- Invert to give the solution of the ODE.
The method is best illustrated by example and we shall need the following results from earlier:
$$\mathscr{L}\,\{x\} = \bar{x}. $$
$$\mathscr{L}\,\{\dot{x}\} = s\bar{x} - x(0) $$
$$\mathscr{L}\,\{\ddot{x}\} = s^2\bar{x} - s\,x(0) - \dot{x}(0)$$
Example 9
Use Laplace transforms to solve the ODE, $\ddot{x} + 2\dot{x} + 5x = 8e^{- 3 t}$ subject to the initial conditions $x(0) = \dot{x}(0) = 0$.
Transform both sides of the ODE ( from left to right use #25, #24, #23 and #5 ):
$$[s^2\,\bar{x} - s\,x(0) - \dot{x}(0)] + 2[s\,\bar{x} - x(0)] + 5\,\bar{x} = \frac{8}{s + 3}$$
Substitute initial values:
$$[s^2\,\bar{x} - s\,0 - 0] + 2[s\,\bar{x} - 0] + 5\,\bar{x} = \frac{8}{s + 3}$$
$$(s^2 + 2s + 5 )\,\bar{x} \;\;\;\;\;\;\;\;\;\;= \frac{8}{s + 3}.$$
Solve for $\bar{x}$:
$$\bar{x} = \frac{8}{(s + 3)(s^2 + 2s + 5)}\;.$$
Manipulate into a form that can be inverted from the tables. In this case we form partial fractions, complete the square on the quadratic denominator and finish up with a little “fine tuning” of the last term:
$$\bar{x} = \bigg[\frac{1}{s + 3}\bigg] - \bigg[\frac{s}{(s + 1)^2 + 2^2}\bigg] + \frac{1}{2}\bigg[\frac{2}{(s + 1) + 2^2}\bigg].$$
Finally invert term-by-term and simplify:
$$x(t) = e^{- 3 t} - e^{- t}\Big[\cos(2t) - \frac{1}{2}\sin(2t)\Big] + \frac{1}{2}e^{-t}\sin(2t)$$
$= e^{- 3 t} - e^{- t} \big[\cos(2t) - \sin(2t)\big]$.
End of Example 9Example 10
Solve $\ddot{x} + 25x = 1$ subject to $x(0) = 10$ and $\dot{x}(0) = 0$ using Laplace transforms.
Transform the ODE:
$$\Big[s^2\bar{x} - s\,x(0) - \dot{x}(0)\Big] + 25\bar{x} = \frac{1}{s}\;. $$
Substitute initial values:
$$\Big[s^2\bar{x} - 10s - 0\Big] + 25\bar{x} = \frac{1}{s}\;. $$
Solve for $\bar{x}$:
$$s^2\bar{x} + 25\bar{x} = \frac{1}{s} + 10s$$
$$(s^2 + 25)\bar{x} = \frac{1}{s} + 10s$$
$$\bar{x} = \frac{1}{s(s^2 + 25)} + 10\frac{s}{(s^2 + 25)}.$$
Manipulate and invert:
$$\bar{x} = \frac{1}{25}\bigg[\frac{25}{s(s^2 + 25)}\bigg] + 10\bigg[\frac{s}{(s^2 + 25)}\bigg]$$
$x(t) = {\Large\frac{1}{25}}\big[1 - \cos(5t)\big] + 10\cos(5t)$. ( # 10 and # 9 from the tables )
End of Example 10Now watch the following:
📹 Solving Homogeneous ODEs using Laplace Transforms
Using Laplace transforms to solve ODEs of the form
$$a\ddot{x} + b\dot{x} + c\,x = f(t)$$
allows us to tackle problems where a solution by the method of undetermined coefficients (say) is rendered difficult or impossible because of the specific type of function on the right-hand-side.
We shall now look at two such functions for which this is the case.
-
6. The Unit Step Function
The unit step function, also known as the Heaviside function, is defined as
$$u(t - T) = \bigg\{\matrix{0\;,\,t < T \\ 1\;,\,t > T}$$
and its graph is shown in the figure below
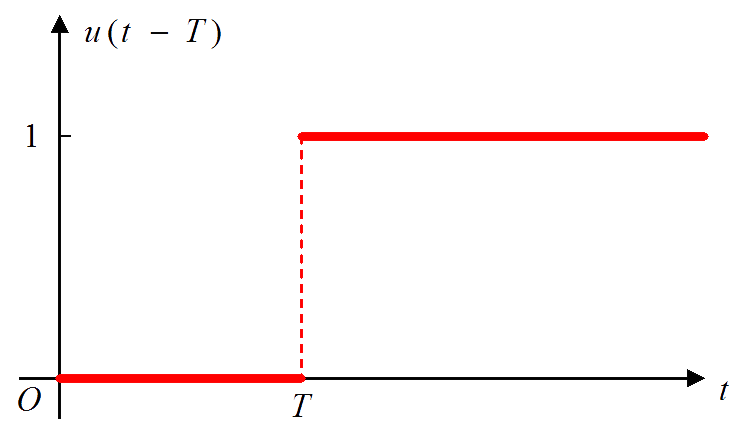
Here $T$ is called the critical value of the step function; it is where the function changes value. The value of the step function at $t = T$ is not defined above. Some authors define the value as 1, others define it as 0 while others define it as 0.5. We shall not worry about it!
The step function is like a mathematical switch. It can be used to model situations where an event occurs suddenly, such as when a circuit is switched on, or a voltage is instantaneously modified, or a force is suddenly applied or removed. The modelling may be done by taking combinations of step functions with different critical values, or even combining them with more conventional functions, as the following examples illustrate.
Note:Since Laplace transforms are only concerned with functions where $t \geqslant 0$, if the step occurs at $t = 0$ then $u(t - 0) \equiv 1$.
Example 11
Sketch the graph of the function $f(t) = 2u(t - 5) - 3u(t - 10) + u(t - 15)$.
- Here it may be useful to think of the step functions as switches and examine the critical values.
- for $t < 5$ all step functions are “off” and are all equal to zero;
- for $5 < t < 10 $ the first step function, $u(t - 5)$, is “on” and has the value 1;
- for $10 < t < 15$ the second step function, $u(t - 10)$, now switches on to 1 also; and
- for $t > 15$ all step functions are now “on” and equal to 1.
We now evaluate $f(t)$ noting that it is a linear combination of the three step functions.
$$ \begin{align*} f(t) = \left\{ \begin{matrix} \;\;0 & , & 0 < t < 5\; \\ \;\;2 & , & 5 < t < 10 \\ -1 & , & 10 < t < 15 \\ \;\;0 & , & t > 15 \end{matrix}\right. \end{align*}$$
The graph of $f(t)$ is shown below
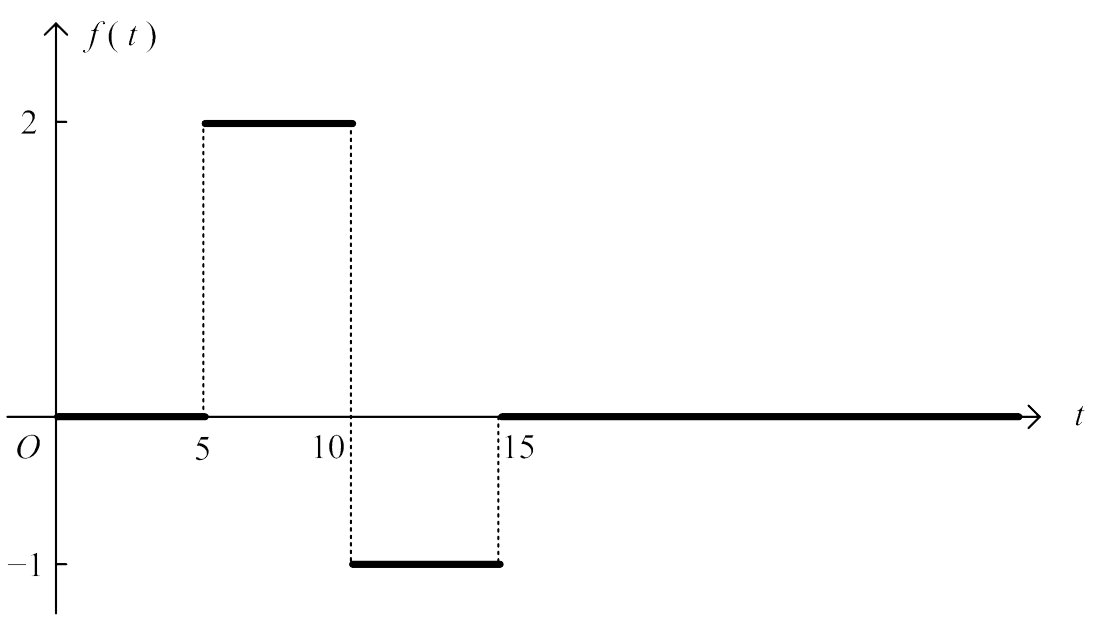 End of Example 11
End of Example 11Example 12
Graph the function, $f(t) = (2 - t)(t - 4)[u(t - 2) - u(t - 4)]$.
We shall do this in two parts. Without the step functions we would have the quadratic function
$$g(t) = (2 - t)(t - 4) = -t^2 + 6t - 8.$$
This graph crosses the $x$-axis at $t = 2$ and $t = 4$ and has a maximum turning point at $(3, 1)$ .
The step functions take the following values:
$$ \begin{align*} u(t - 2) - u(t - 4) = \left\{ \begin{matrix} 0 - 0 = 0\ & , & t < 2 \\ 1 - 0 = 1 & , & 2 < t < 4 \\ 1 - 1 = 0 & , & t > 4 \end{matrix}\right. \end{align*}.$$
When the two parts ( quadratic and step functions ) are multiplied together we obtain
$$ \begin{align*} f(t) = \left\{ \begin{matrix} 0 & , & t < 2 \\-t^2 + 6t - 8 & , & 2 < t < 4 \\ 0 & , & t > 4 \end{matrix}\right. \end{align*} $$
resulting in the graph below
We can think of a difference of two step functions
$$u(t - a) - u(t - b)$$
like a “mathematical window” whose frame obscures the graph of any multiplying function to the sides, i.e. for $t < a$ and $t > b$.
In the previous example by including the “mathematical window”, $u(t - 2) - u(t - 4)$, the quadratic function $g(t) = -t^2 + 6t - 8$ was obscured outside the window, i.e. set to zero for $t < 2$ and $t > 4$.
End of Example 12The following examples demonstrate how to determine a function, that involves step functions, from its graph.
Example 13
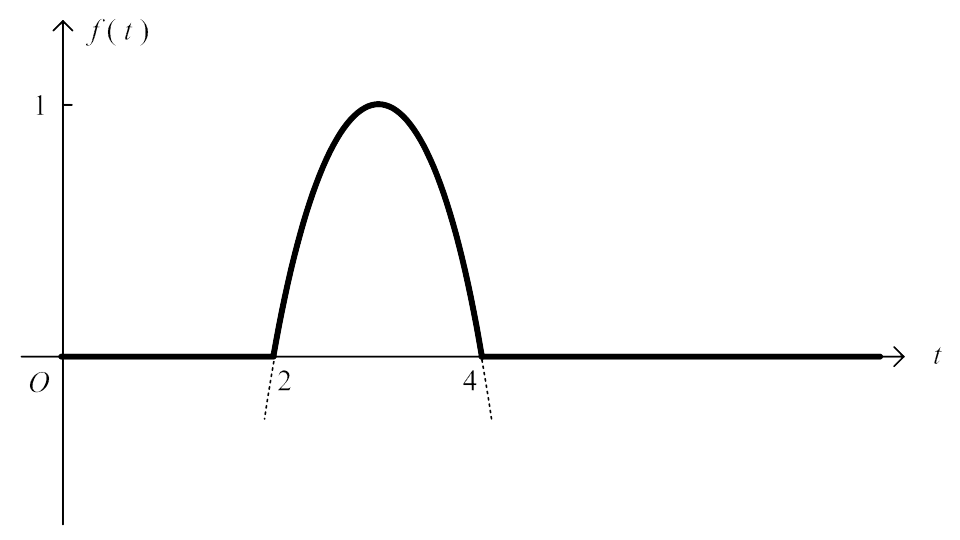
Determine $f(t)$ from the following graph:
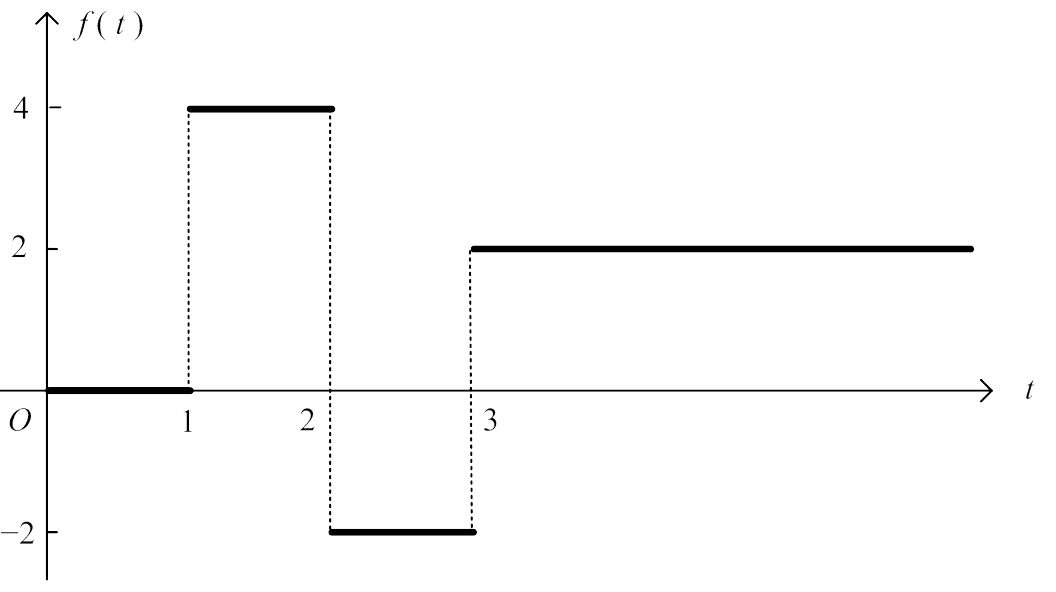
The jumps in the graph can be represented by step functions. The location of the jump is determined by the critical value of the step function, the size of the jump can be achieved by multiplying the step function by a suitably sized constant, the direction of the jump is obtained from the sign of the constant.
Working from left to right:
1st jump: $4u(t - 1)$ up to $4$ at $T = 1$
2nd jump: $-6u(t - 2)$ down by $6$ at $T = 2$
3rd jump: $4u(t - 3)$ up by $4$ at $T = 3$.
Adding these together gives us the function:
$f(t) = 4u(t - 1) - 6u(t - 2) + 4u(t - 3)$.
End of Example 13Example 14
Determine $f(t)$ from the following graph:
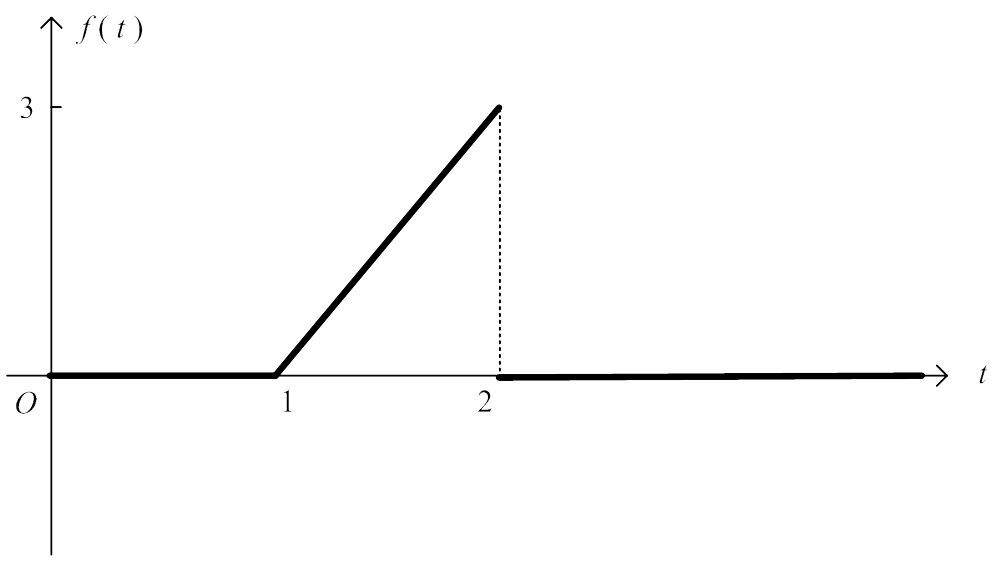
Using basic coordinate geometry the equation of the oblique straight line is given by
$$y = 3t - 3.$$
The straight line is only visible between $t = 1$ and $t = 2$ with the function taking the value zero outside this interval, i.e. for $t < 1$ and $t > 2$. Hence, we have the “mathematical window”,
$$u(t - 1) - u(t - 2).$$
Multiplying the two parts together gives us our function:
$f(t) = (3t - 3)[u(t - 1) - u(t - 2)]$.
End of Example 14For more general piecewise functions we can break them down into fragments, each with their own window, and add the parts together.
Example 15
Write down the following function in terms of step functions:
$$ \begin{align*} f(t) = \left\{ \begin{matrix} t & , & 0 <t <1 \\ 2 - t & , & 1 < t < 2 \\ 0 & , & t > 2 \end{matrix}\right. \end{align*}.$$
Examine the function $f(t)$ over each of the given intervals.
On the interval $0 < t < 1$, $f(t) = t$ giving, $t\big[u(t - 0) - u(t - 1)\big]$.
On the interval $1 < t < 2$, $f(t) = 2 - t$ giving, $(2 - t)\big[u(t - 1) - u(t - 2)\big]$.
For $t > 2,\; f(t) = 0$.
Combining the above gives
$$f(t) = t\big[u(t - 0) - u(t - 1)\big] + (2 - t)\big[u(t - 1) - u(t - 2)\big].$$
As far as Laplace transforms are concerned $u(t - 0) \equiv 1$ so the above can be rewritten as
$f(t) = t - 2(t - 1)u(t - 1) + (t - 2)u(t - 2)$.
End of Example 15There are two results that we shall need in order to solve ODEs containing step functions.
Result 1 - Laplace transform of the unit step function
$$\mathscr{L}\,\{u(t - T)\} = \frac{1}{s}e^{- s\,T}$$
Proof
$$\mathscr{L}\,\{u(t - T)\} = \int_{0}^{\infty}\,u(t - T)\,e^{- s t}\,dt$$
$$= \int_{0}^{T}\,0.e^{-st}\,dt + \int_{T}^{\infty}\,1.e^{-st}\,dt$$
$$=\;\;\;\;\;\;\;0\;\;\;\;\;\;\;\;\;\;\;+ \bigg[-\frac{1}{s}e^{-st}\bigg]_{T}^{\infty} $$
$$= \frac{1}{s}e^{-sT}\;\;\;\;\;\;\;\;(s > 0).$$
Now watch the following:
📹 Find the Laplace Transform of a Step Function - method 1
📹 Find the Laplace Transform of a Step Function - method 2
Result 2 – The Second Shifting Theorem
Given a function $f(t)$ with Laplace transform $F(s)$, it can be shown that
$$\mathscr{L}\,\{f(t - T)u(t - T)\} = F(s)e^{-sT}.$$
The proof of this is omitted. The implication of this result is demonstrated graphically in the figure below.
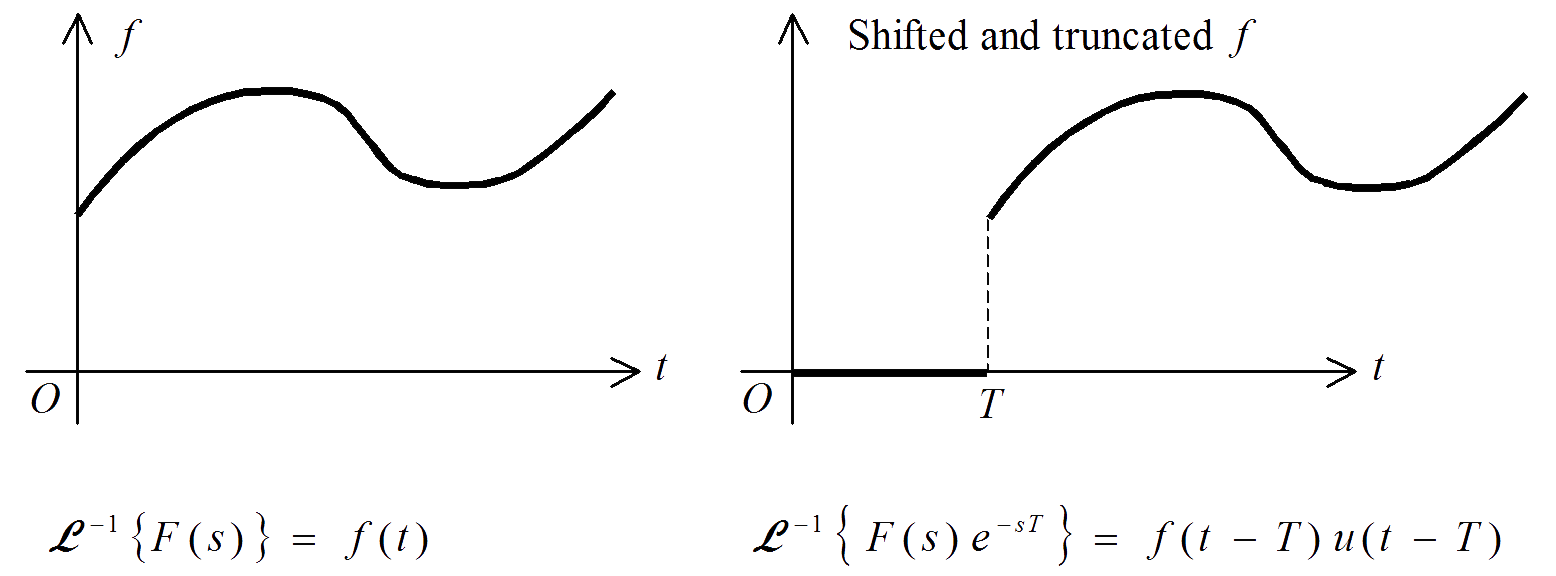
Now watch the following:
In our work we shall use modified versions of the following diagram to help us apply the Second Shifting Theorem (SST):
$$\class{outbox}{\matrix{f(t) & \leftrightarrow & F(s) \\ \updownarrow & & \updownarrow \\f(t - T)u(t - T) & \leftrightarrow & F(s)e^{-sT}}}$$
Example 16
Determine $\mathscr{L}\,\{t^2u(t - 10)\}$.
To calculate LTs using the SST we start at the bottom-left of the diagram and move round in a clockwise direction ending up in the bottom-right and obtaining the result:
$$\class{outbox}{\matrix{f(t) & \rightarrow & F(s) \\ \uparrow & & \downarrow \\ f(t - T)u(t - T) & & F(s)e^{-sT}}}$$
However, we have a slight problem in that the given function of $t$ does not quite conform to the structure in the bottom-left. We need to rewrite the multiplying function $t^2$ so that any occurrence of the variable $t$ always includes a “minus $T$ ”. For this example $T = 10$ so we introduce it as follows:
$$t^2 = \big[(t - 10) + 10\big]^2 = (t - 10)^2 + 20(t - 10) + 100 .$$
The original function becomes $\big[(t - 10)^2 + 20(t - 10) + 100\big]u(t - 10)$ which now does conform. Next we use the SST to transform:
Step 1: Cover up the step function and the “minus 10s” to leave
$$f(t) = t^2 + 20t + 100.$$
Step 2: Transform to give $F(s) = {\Large\frac{2}{s^3}} + {\Large\frac{20}{s^2}} + {\Large\frac{100}{s}}$.
Step 3: Everything we covered up in Step 1 is now accounted for by multiplying $F(s)$ by $e^{-10s}$ and so completes the transformation,
$\mathscr{L}\,\{t^2u(t - 10)\} = \;$ $\bigg[{\Large\frac{2}{s^3}} + {\Large\frac{20}{s^2}} + {\Large\frac{100}{s}}\bigg]e^{-10s}$.
End of Example 16Example 17
Invert the Laplace transform ${\Large\frac{1}{s(s + 2)}}e^{-4s}$.
To invert LTs, using the SST, we start at the bottom-right of the diagram and move round in an anticlockwise direction ending up in the bottom-left and obtaining the result:
$$\class{outbox}{\matrix{f(t) &\leftarrow & F(s) \\ \downarrow & & \uparrow \\f(t - T)u(t - T) & & F(s)e^{-sT}}}$$
Step 1: Ignore exponential to give $F(s) = {\Large\frac{1}{s(s + 2)}} = {\Large\frac{1}{2}}\bigg[{\Large\frac{2}{s(s + 2)}}\bigg]$.
Step 2: Invert $F(s)$ to give $f(t) = {\Large\frac{1}{2}}\big[1 - e^{-2t}\big]$.
Step 3: Shift and truncate with $T = 4$, i.e. replace $t$ in $f(t)$ by $(t - 4)$ and multiply by $u(t - 4)$, to give the completed inversion $f(t - T)u(t - T)$. Hence,
$\mathscr{L}^{-1} \bigg\{{\Large\frac{1}{s(s + 2)}}e^{-4s}\bigg\} = \;$ ${\Large\frac{1}{2}}\big[1 - e^{-2(t - 4)}\big]u(t - 4)$.
End of Example 17Example 18
Solve the differential equation $\ddot{x} + 4x = u(t - 3)$ subject to $x(0) = \dot{x}(0) = 0$.
Transform: $\big[s^2\bar{x} - s\,x(0) - \dot{x}(0)\big] + 4\bar{x} = {\Large\frac{1}{s}}e^{-3s}$
Substitute initial conditions and solve for $\bar{x}$:
$$(s^2 + 4)\bar{x} = \frac{1}{s}e^{-3s}$$
so
$$\bar{x} = \frac{1}{s(s^2 + 4)}e^{-3s}.$$
Invert with the help of the Second Shifting Theorem:
Again, we are starting at the bottom-right of the diagram and moving round anti-clockwise:
$$\class{outbox}{\matrix{f(t) & \leftarrow & F(s) \\ \downarrow & & \uparrow \\ f(t - T)u(t - T) & & F(s)e^{-sT}}} $$
Step 1: Ignore exponential to give $F(s) = {\Large\frac{1}{s(s^2 + 4)}} = {\Large\frac{1}{4}}\bigg[{\Large\frac{2^2}{s(s^2 + 2^2)}}\bigg]$.
Step 2: Invert $F(s)$ to give $f(t) = {\Large\frac{1}{4}}\big[1 - \cos(2t)\big]$.
Step 3: Shift and truncate with $T = 3$, i.e. in $f(t)\,$ replace $t$ by $(t - 3)$ and multiply by $u(t - 3)$ to give $f(t - T)u(t - T)$ and the completed solution,
$x(t) = {\Large\frac{1}{4}}\big[1 - \cos(2(t - 3))\big]u(t - 3)$.
End of Example 18Now watch the following:
📹 Solving ODEs Involving Step Functions using Laplace Transforms
The two previous examples illustrate the use of the SST to invert Laplace transforms that contain an exponential factor. The next example shows the theorem working in the opposite direction.
We now look at another new type of function, one that is closely related to the step function.
-
7. The Dirac Delta Function
The Dirac delta function at the point $t = T$ is denoted $\delta(t - T)$ and it is defined to be the derivative of the unit step function, i.e.
$$\delta(t - T) = \frac{d}{dt}u(t - T).$$
It is often used to model actions or events in mechanical and electrical systems that exert a large force over a short period of time. Examples include a hammer striking an object, a short in an electrical circuit or a lightning strike. It is also referred to as the impulse function.
We now briefly look at the derivation of the Dirac delta function and some of its properties.
Consider the function
$$D_\varepsilon(t) = \bigg\{\matrix{1/2\varepsilon & , & T - \varepsilon \le t \le T + \varepsilon \\ 0 & , & \text{otherwise}\;\;\;\;\;\;\;\;\;\;\;\;\;\; }$$
where $\varepsilon > 0$, shown in the figure below:
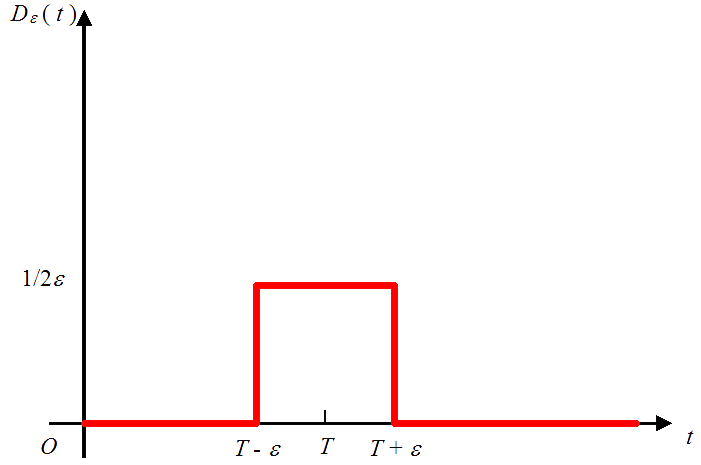
If the area under the rectangular section is defined to always equal 1 then it is clear that by letting $\varepsilon \rightarrow 0$, so that the width of the interval about $T$ shrinks towards zero, then the height must increase towards infinity ( in such a way that the area under the graph is always 1 ). In the limit, we obtain an “instantaneous, infinite blip” at $t = T$. This “infinite blip” at $ t = T$ is called the Dirac delta function and its graph is shown in the figure below
The Dirac delta function has the following properties:
(i). $\delta(t - T) = 0$, $t \neq T\;$ It is zero everywhere except at the point where $t = T$ and at this point it has infinite value.
(ii). ${\huge\int}_{- \infty}^{+ \infty} \delta(t - T)\; dt = 1$, the integral over any interval containing the point $t = T$ has the value 1.
(iii). ${\huge\int}_{- \infty}^{+ \infty} \delta(t - T)\,f(t)\,dt = f(T)$.
Using the third property we can determine the Laplace transform of the Dirac delta function:
$$\mathscr{L}\{\delta(t - T)\} = \int_{0}^{\infty} \delta(t - T)\,e^{- s t}\,dt = \int_{- \infty}^{+ \infty} \delta(t - T)\,e^{- s t}\,dt = e^{- sT}.$$
Strictly speaking the Dirac delta function is not a function in the usual sense as a function that is zero everywhere except at a single point will evaluate to zero when integrated. However, for our purposes it is convenient to regard it as an ordinary function.
Example 19
Solve the differential equation $\dot{x} + 4x = 3\,\delta(t - 2)\;,\; x(0) = 5$.
Transform: $\big[s\bar{x} - x(0)\big] + 4\bar{x} = 3e^{-2s}$.
Substitute initial condition and solve for $\bar{x}$:
$$(s + 4)\;\bar{x} = 3e^{-2s} + 5$$
$$\bar{x} = \frac{3}{(s + 4)}e^{-2s} + \frac{5}{(s + 4)}.$$
$[A] \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;[B]$
Invert to give solution:
$$[A]: \;\;\;\;\;\mathscr{L}^{-1}\bigg\{\frac{3}{(s + 4)}\bigg\} = 3\,e^{-4t}.$$
By the Second Shifting Theorem,
$$\mathscr{L}^{-1} \bigg\{\frac{3}{(s + 4)}e^{-2s}\bigg\} = 3\,e^{-4(t - 2)}u(t - 2)$$
$$[B]: \;\;\;\;\;\mathscr{L}^{-1}\bigg\{\frac{5}{(s + 4)}\bigg\} = 5\,e^{-4t}$$
Combine $[A]$ and $[B]$ above to obtain the solution:
$x(t) = 3e^{-4(t - 2)}u(t - 2) + 5\,e^{-4t}$.
End of Example 19Example 20
In a branch of an electronic circuit the variation of current with time is modelled by the differential equation
$$\frac{d^2i}{dt^2} + 36i = \frac{dV}{dt},$$
where $V(t)$ is an input voltage. Suppose $V(t) = 240[u(t - 5) - u(t - 10)]$. Assuming zero initial conditions, determine the current, $i$, as a function of time, $t$ .
Solution
Recalling that the Dirac delta function is the derivative of the unit step function we can write
$$\frac{dV}{dt} = 240[\delta(t - 5) - \delta(t - 10)]$$
and so the differential equation becomes
$$\frac{d^2i}{dt^2} + 36i = 240[\delta(t - 5) - \delta(t - 10)].$$
The Laplace transformation process results in
$$\bar{i} = \frac{240}{s^2 + 36}[e^{-5s} - e^{-10s}],$$
which can be inverted with the help of the Second Shifting Theorem to give the solution:
$i(t) = 40\,\sin[6(t - 5)]u(t - 5) - 40\,\sin[6(t - 10)]u(t - 10)$.
End of Example 20Earlier in the notes we encountered the warning below:
The Laplace transform of a product is NOT EQUAL TO the product of the individual Laplace transforms.
We shall now look at a kind of product rule for Laplace transforms.
-
8. Convolution
The convolution of two functions $f(t)$ and $g(t)$ is another function of $t$ denoted by $f * g$ and defined by
$$f * g = \int_{0}^{t}\,f(t - z)\,g(z)\,dz \;\;\;\;\;\;\;\;\;\;\;\;\;\;[a]$$
or
$$f * g = \int_{0}^{t}\,f(z)\,g(t - z)\,dz. \;\;\;\;\;\;\;\;\;\;\;\;\;[b]$$
It can be shown that these two integrals are equal.
If $F(s)$ and $G(s)$ are the Laplace transforms of $f(t)$ and $g(t)$ respectively, then
$$\mathscr{L}\{f * g\} = F(s)G(s).$$
Example 21
Invert the Laplace transform ${\Large\frac{1}{s(s + 4)^2}}$.
The solution could be obtained using partial fractions (try it!), but convolution can be used as an alternative:
Set $F(s) = {\Large\frac{1}{s}}$ and $G(s) = {\Large\frac{1}{(s + 4)^2}}$ and invert individually from the tables to obtain:
$f(t) = 1$ and$g(t) = te^{-4t}$.
Form the convolution of $f$ and $g$ using form $[a]$ above :
$f(t - z) = 1$, $g(z) = ze^{-4z}$
$$f * g = \int_{0}^{t}\, f(t - z)\,g(z)\,dz$$
$$= \int_{0}^{t}\,z\,e^{-4z}\,dz. $$
Omitting the details, integration by parts gives
$f * g = - {\Large\frac{1}{4}}t\,e^{-4t} - {\Large\frac{1}{16}}e^{-4t} + {\Large\frac{1}{16}}$.
End of Example 21Now watch the following:
-
9. A Note on Control Theory
As mentioned earlier, Laplace transforms are an important tool in control theory. Keeping things basic, in a simple control system there may be an input and an output. Control theory is concerned with the relationship between the input and the output within the system. Often a control system can be modelled by a differential equation that relates input to output in what may be referred to as the time domain. For example, a differential equation such as
$$\frac{dx}{dt} + k\,x = v(t)$$
might relate an input $v(t)$ to an output $x(t)$. For a given input the equation is solved to give the corresponding output. However, in control theory options regarding the input are often left open. Without a specific input, we cannot determine a corresponding output, but valuable information about the system's controllability can be established by leaving the input unspecified, and continuing to apply the solution process to the differential equation in any case.
For the differential equation given above denote the following Laplace transforms:
$$\mathscr{L}\,\{x(t)\} = X(s), \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathscr{L}\,\{v(t)\} = V(s).$$
Taking the LT of the ODE, assuming that the initial condition of $x(t)$ is zero, gives:
$$s\,X(s) + k\,X(s) = V(s).$$
Rearranging this expression yields:
$$(s + k)\,X(s) = V(s)$$
or
$$\frac{X(s)}{V(s)} = \frac{1}{(s + k)}.$$
What we have here is the ratio of the output of the system to its input in what is called the Laplace domain. In control theory this ratio is called the system’s transfer function.
In general, for a system with a single input and a single output we have
$$\frac{X(s)}{V(s)} = H(s).$$
The transfer function $H(s)$ is itself a Laplace transform and its form will depend on the structure of the differential equation modelling the system. The transfer function is of critical importance in control theory as much information can be derived from it. However, that is another story for another module!
-
Summary
- This unit has introduced the Laplace transform which in an integral transform that is extensively used in physics and engineering applications to solve problems, in particular differential equations, that would otherwise be difficult, or even impossible, to solve using standard methods. You should now be able to:
- calculate the Laplace transform of a basic function directly from the definition.
- determine Laplace transforms and inverse Laplace transforms of various functions from tables of Laplace transforms.
- solve first and second order differential equations involving standard forcing functions using Laplace transforms.
- understand basic properties of the unit step function and the Dirac delta (impulse) function.
- solve first and second order differential equations involving unit step functions and Dirac delta (impulse) functions using Laplace transforms.
-
TABLE OF LAPLACE TRANSFORMS
$\mathscr{L}\,\{f(t)\}$ is defined by ${\LARGE\int}_{0}^{\infty}\,f(t)\,e^{-st}\,dt$
$f(t)$ $f(s) = \mathscr{L}\,\{f(t)\}$ 1 $1$ ${\Large\frac{1}{s}}$ 2 $t$ ${\Large\frac{1}{s^2}}$ 3 $t^2$ ${\Large\frac{2}{s^3}}$ 4 $t^n$ ${\Large\frac{n!}{s^{n + 1}}}$ 5 $e^{-\alpha t}$ ${\Large\frac{1}{(s + \alpha)}}$ 6 $t\,e^{- \alpha t}$ ${\Large\frac{1}{(s + \alpha)^2}}$ 7 $1 - e^{- \alpha t}$ ${\Large\frac{\alpha}{s(s + \alpha)}}$ 8 $\sin\,(\omega\,t)$ ${\Large\frac{\omega}{s^2 + \omega^2}}$ 9 $\cos\,(\omega\,t)$ ${\Large\frac{s}{s^2 + \omega^2}}$ 10 $1 - \cos\,(\omega\,t)$ ${\Large\frac{\omega^2}{s(s^2 + \omega^2)}}$ 11 $\omega\,t\,\sin\,(\omega\,t)$ ${\Large\frac{2\,\omega^2\,s}{(s^2 \;+\; \omega^2)^2}}$ 12 $\sin\,(\omega\,t) - \omega\,t\,\cos\,(\omega\,t)$ ${\Large\frac{2\,\omega^3}{(s^2\,+\,\omega^2)^2}}$ 13 $\sin\,(\omega\,t \, + \, \phi)$ ${\Large\frac{s\,\sin\,\phi\, + \, \omega\,\cos\,\phi}{s^2 \, + \, \omega^2}}$ 14 $e^{- \alpha t}\,\sin\,(\omega\,t)$ ${\Large\frac{\omega}{(s\, + \,\alpha)^2 \, + \, \omega^2}}$ 15 $e^{- \alpha t}\,\cos\,(\omega\,t)$ ${\Large\frac{s\,+\,\alpha}{(s\,+\,\alpha)^2\,+\, \omega^2}}$ 16 $e^{- \alpha t}\bigg(\cos\,(\omega\,t) - {\Large\frac{\alpha}{\omega}}\sin\,(\omega\,t)\bigg)$ ${\Large\frac{s}{(s\,+\,\alpha)^2\,+\,\omega^2}}$ 17 $e^{- \alpha t} + {\Large\frac{\alpha}{\omega}}\sin\,(\omega\,t) - \cos\,(\omega\,t)$ ${\Large\frac{\alpha^2 \, + \, \omega^2}{(s\,+\,\alpha)(s^2 \, + \, \omega^2)}}$ 18 $\sinh\,(\beta\,t)$ ${\Large\frac{\beta}{s^2 \,-\, \beta^2}}$ 19 $e^{- \alpha t}\,\sinh\,(\beta\,t)$ ${\Large\frac{\beta}{(s\,+\,\alpha)^2\,-\,\beta^2}}$ 20 $\cosh\,(\beta\,t)$ ${\Large\frac{s}{s^2\,-\,\beta^2}}$ 21 $e^{-\alpha t}\,\cosh\,(\beta\,t)$ ${\Large\frac{s\,+\,\alpha}{(s\,+\,\alpha)^2\,-\,\beta^2}}$ 22 $e^{- \alpha t}\,f(t)$ $F\,(s\,+\,\alpha)$ 23 $x$ $\bar{x}$ 24 $\dot{x}$ $s\,\bar{x} - x(0)$ 25 $\ddot{x}$ $s^2\,\bar{x} - s\,x(0) - \dot{x}(0)$ Unit Step Function 26 $u\,(t - T) = \bigg\{\matrix{0 & , & t < T \\1 & , & t > T}$ ${\Large\frac{1}{s}}e^{-sT}$ 27 $f\,(t - T)\,u\,(t - T)$ $F\,(s)\,e^{-sT}$ Dirac Delta Function 28 $\delta\,(t)$ $1$ 29 $\delta\,(t - T)$ $e^{-sT}$ Convolution Integral 30 ${\LARGE\int}_{0}^{t}\,f(z)\,g(t - z)\,dz$
OR
${\LARGE\int}_{0}^{t}\,f(t - z)\,g(z)\,dz$$F(s)\,G(s)$