02
  • Do Not Click on the 'Main Menu' button, this action will erase the entire page !


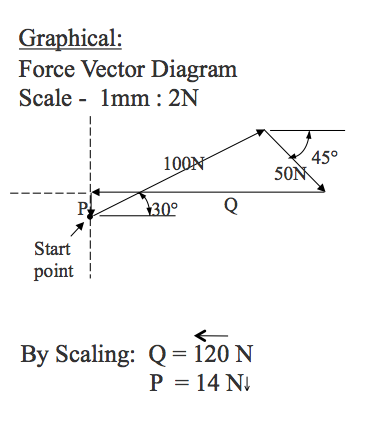
  • The forces shown in Figure Ex.1 are concurrent and in equilibrium. Determine the magnitude of the forces P and Q:
    •analytically;
    •graphically using vector diagrams.

    force vector diagramanalytical math equation

    2 Dimensional Force Equilibrium

    Worked Example No.1

    The forces shown in Figure Ex.1 are concurrent and in equilibrium.
    Determine the magnitude of the forces P and Q:
    i) analytically;
    ii) graphically using vector diagrams

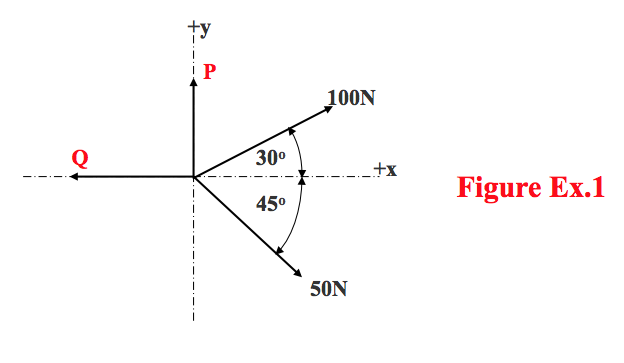
    figure 1

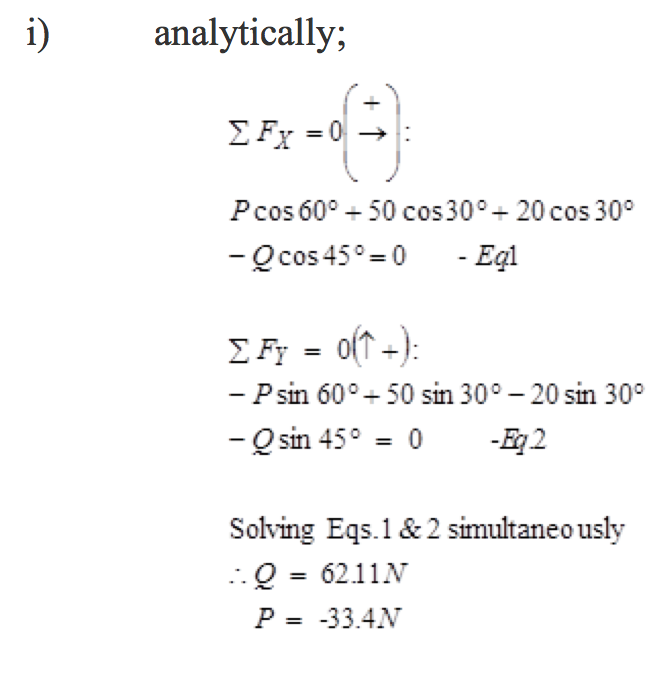
  • analytical math equation for example 2
    vector diagram

    2 Dimensional Force Equilibrium

    Worked Example No.2

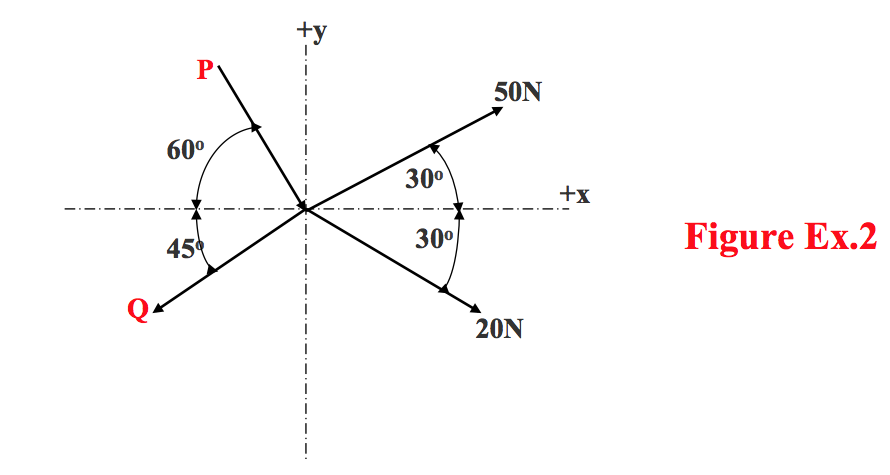
    The forces shown in Figure Ex.2 are concurrent and in equilibrium. Determine the magnitude of the forces P and Q:
    i) analytically;
    ii) graphically using vector diagrams.

    figure exmple 2
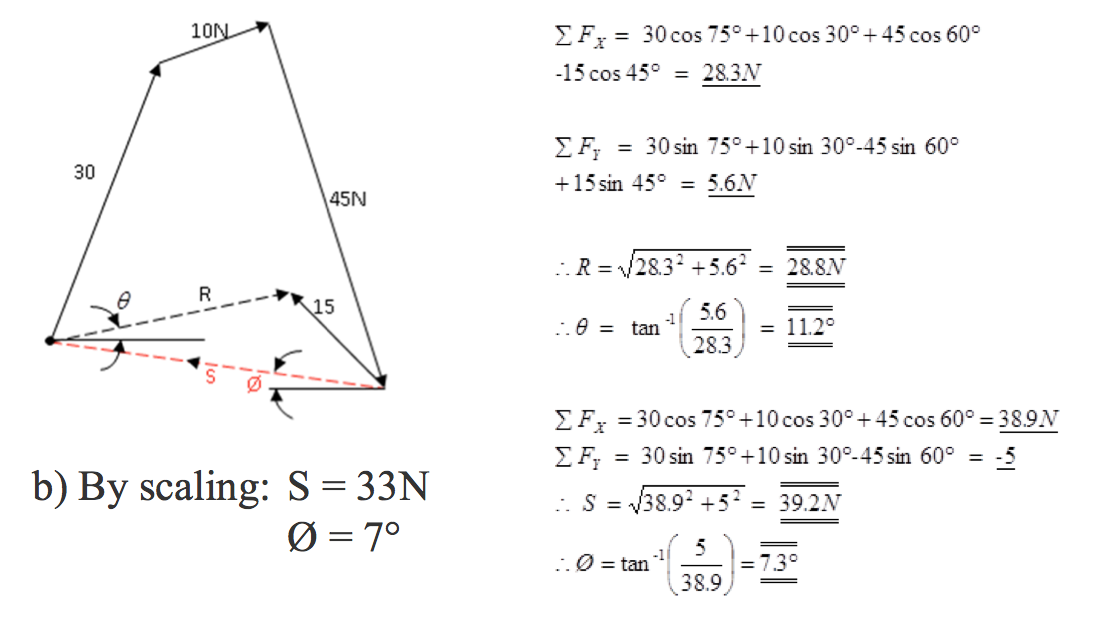
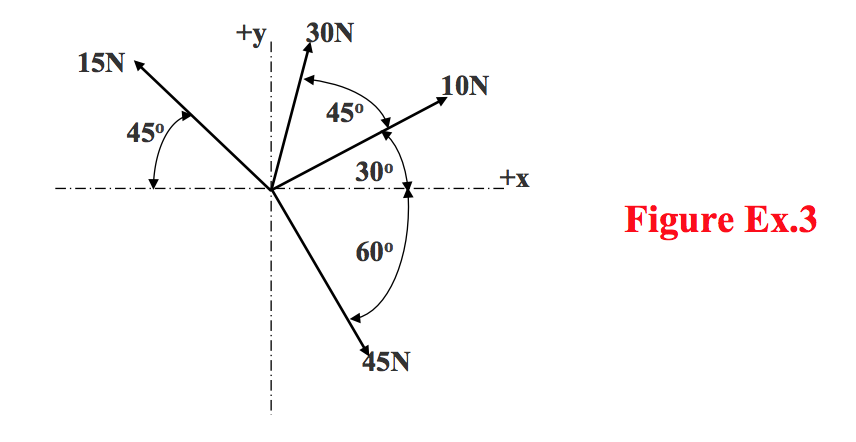
  • i) Find the resultant of the system of concurrent coplanar forces shown in Figure Ex.3 by constructing a vector diagram.
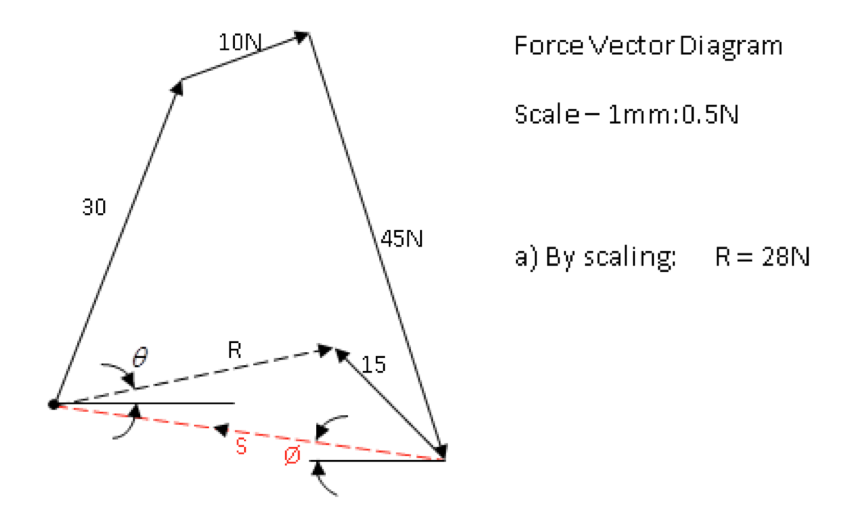
    force vector diagram for example 3
    ii) Replace the 15N force with a new force such that the force system will be in equilibrium.
    analytical math diagram for example 3

    2 Dimensional Force Equilibrium

    Worked Example No.3

    i) Find the resultant of the system of concurrent coplanar forces shown in Figure Ex.3 by constructing a vector diagram.

    ii) Replace the 15N force with a new force such that the force system will be in equilibrium.

    digure example 3

  • 2 Dimensional Equilibrium: The Moment of a Force


    Moment is the turning effect of a force about an axis and is defined as the product of the force and the perpendicular distance from the reference point to the line of action of the force. Figure 5 shows a force of magnitude F acting at a distance d from end point A.

    Figure 5 showing a force of magnitude F acting at a distance d from end point A
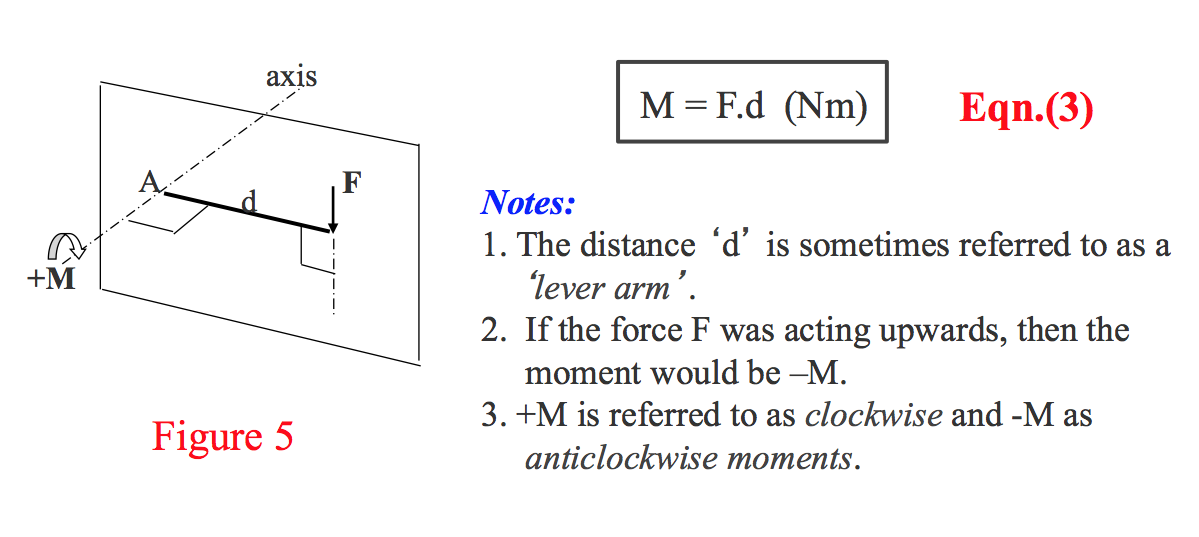
    As stated previously, a rigid body is in equilibrium when the resultant of any force system acting on it is zero, and that the sum of force components acting horizontally and vertically are zero [Eqns.(1) and (2)]. Hence in addition to this, the sum of all moments acting on the body must also add to zero, i.e.
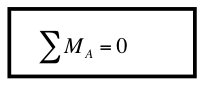    Eqn.(4)

    Hence for 2-dimensional equilibrium, a rigid body has 3 degrees-of-freedom in a plane, i.e. two of translation (displacement) and one of rotation, and the body is in equilibrium when all three are fully restrained. Summarising, the conditions that are required to satisfy the static equilibrium of a 2-dimensional structure are:
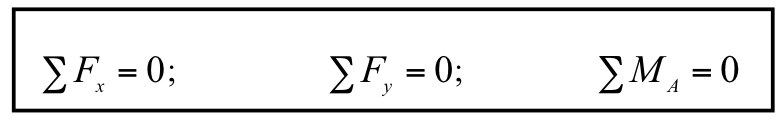
    math equations








  • math equation for example 4

    2 Dimensional Equilibrium

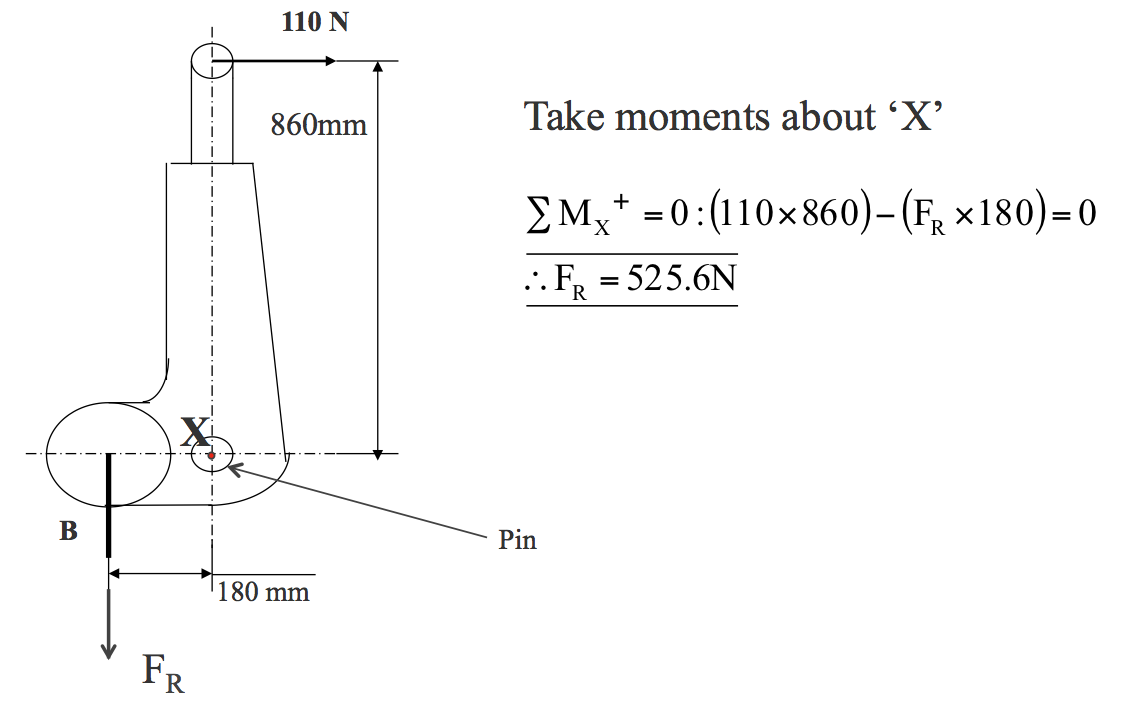
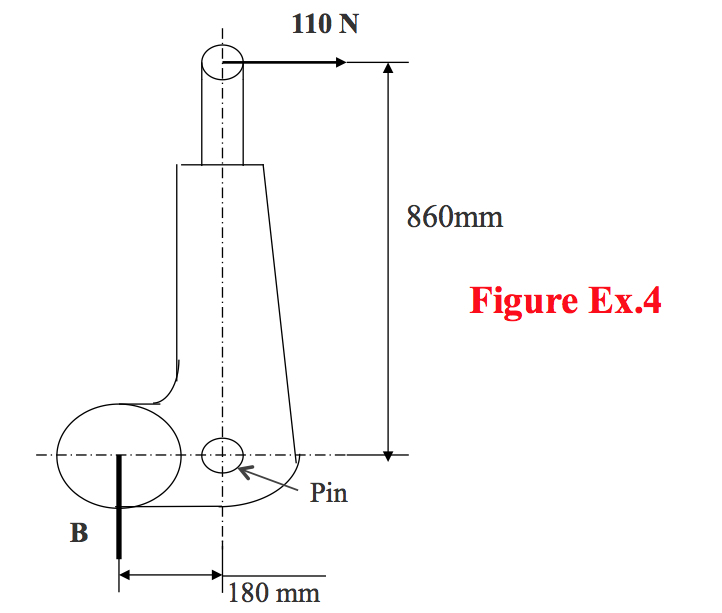
    Worked Example No.4

    A hand brake lever has a force of 110 N applied to it as shown in Figure Ex.4. Calculate the resisting pull in the hand brake cable at B and the direction in which it acts.

    figure example 4

  • 2 Dimensional Equilibrium

    Worked Example No.5

    A vertical structure is subjected to the loads shown in Figure Ex.5.
    If the structure is in equilibrium, determine:
    i) the load ‘W’;
    ii) the vertical distance ‘x’.

    figure example 5
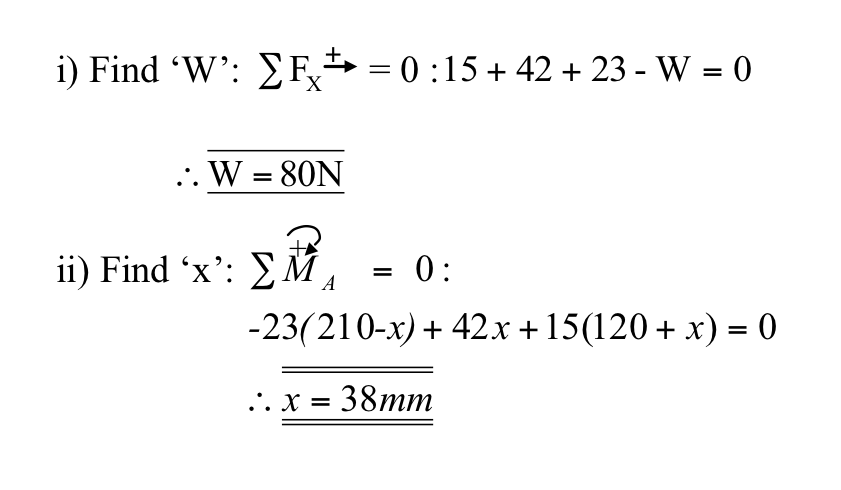
    math equation for example 5
  • detailed figure example 6
    math equation for example 6

    2 Dimensional Equilibrium

    Worked Example No.6

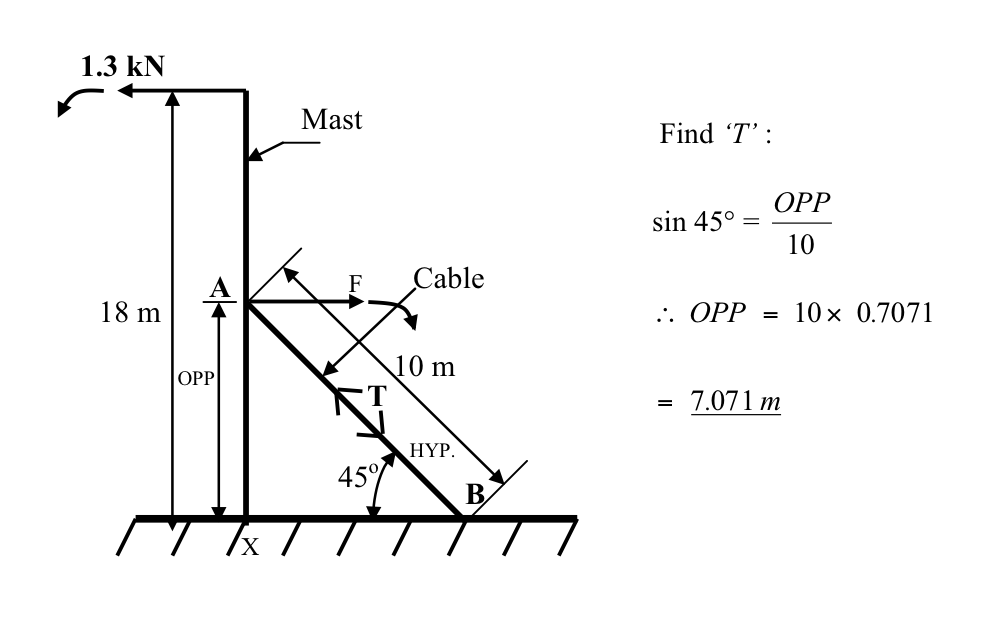
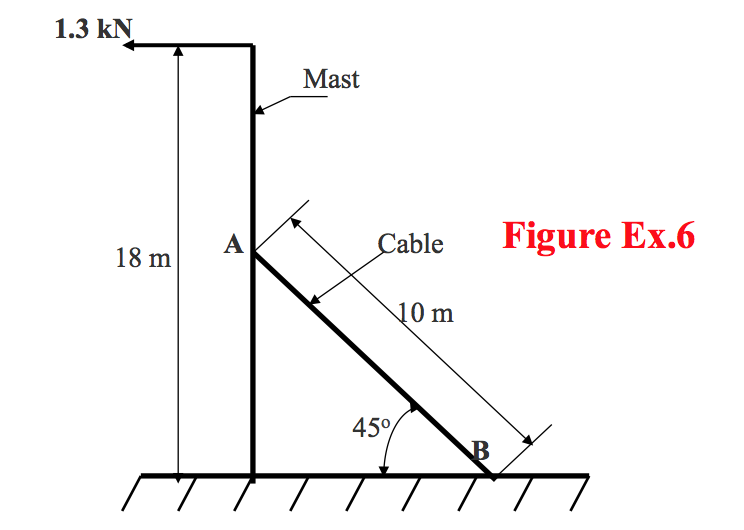
    A mobile telephone mast is held in position as shown by the free-body diagram in Figure Ex.6.
    Calculate the tension in the cable AB when, due to wind loading, a force of 1.3 kN is applied at the position and in the direction shown.

    figure example 6



  • Sample Problem sheet 2_1
    Sample Problem sheet 2_2
    Sample Problem sheet 2_5
    Sample Problem sheet 2_7-8