Skip to main content

Maths Summer School

10 Vectors exercises - Solutions

This section contains solutions to the bonus exercises to accompany the Vectors chapter. Each chapter contained embedded examples and exercises, often with explanations.

These solutions are provided with fewer explanations, generally just with the basic answers provided later. Of course, you can ask questions of the course lecturer about any problems here too.

10.1 Vector sketching

  1. Sketch the following vectors (given in polar format) starting from the specified points:
    1. \((2,30^{\circ})\) starting from \((-3,2)\).
    2. \((5,30^{\circ})\) starting from \((1,4)\).
    3. \((0.25,200^{\circ})\) starting from \((5,4)\).
    4. \((6,-30^{\circ})\) starting from \((-2,2)\).
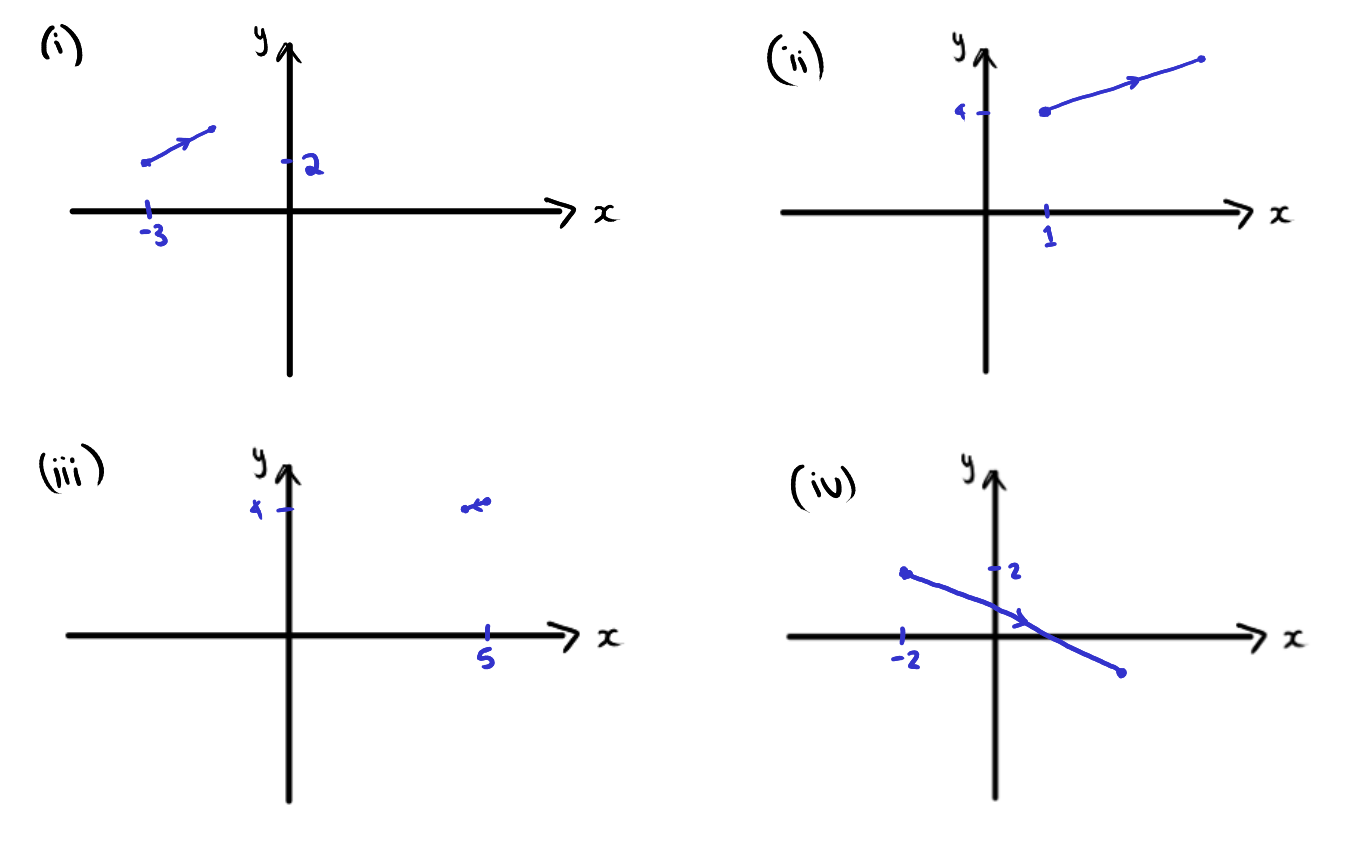
Sketches for question 1

Figure 4.4: Sketches for question 1

  1. Sketch the following vectors (given in the rectangular format) starting from the specified points:
    1. \(\begin{pmatrix}3 \\ 4 \end{pmatrix}\) starting from \((2,1)\).
    2. \(\begin{pmatrix}-4 \\ 2 \end{pmatrix}\) starting from \((2,-4)\).
    3. \(\begin{pmatrix}6.5 \\ 3.5 \end{pmatrix}\) starting from \((-4,-4)\).
    4. \(\begin{pmatrix}-2.5 \\ -4.5 \end{pmatrix}\) starting from \((-6,2)\).
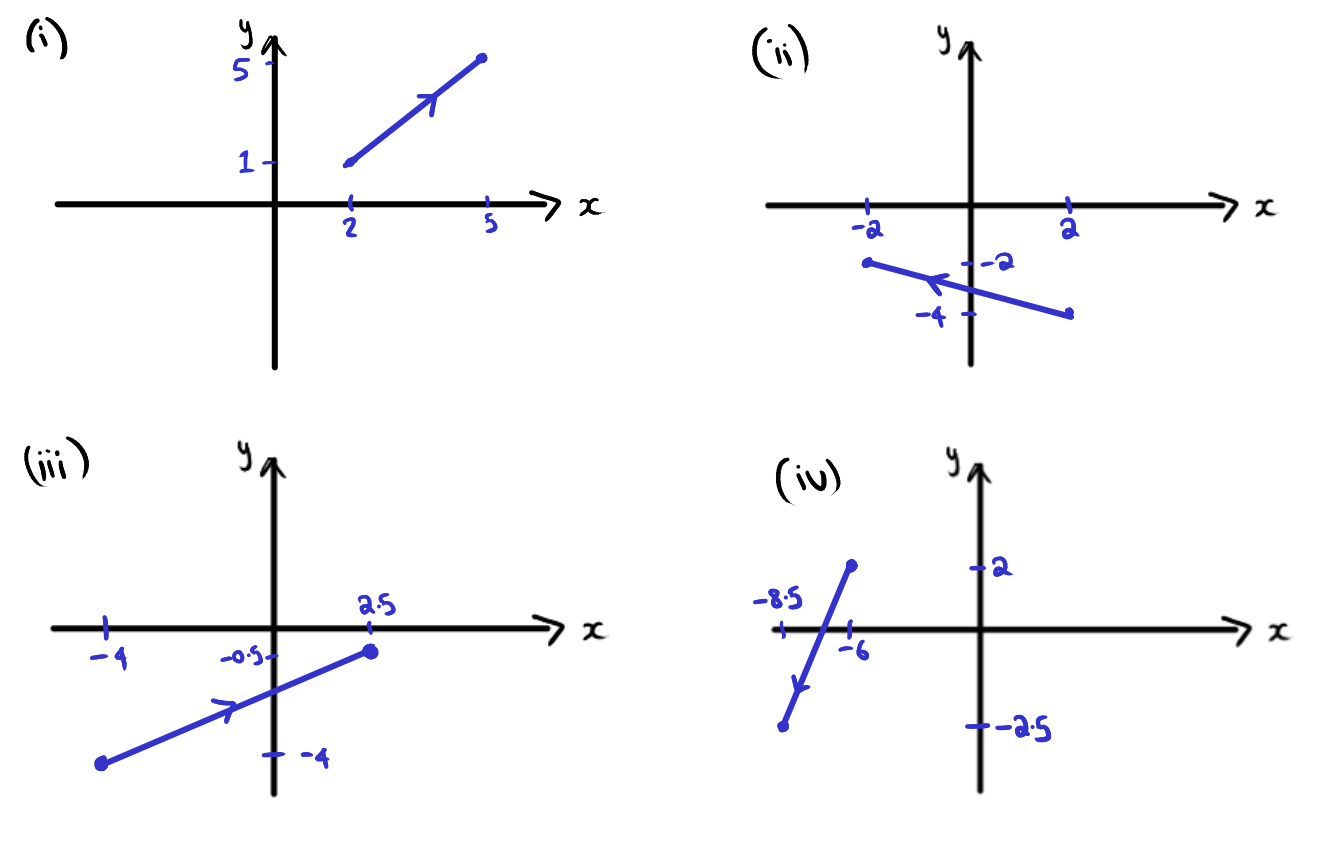
Sketches for question 2

Figure 4.5: Sketches for question 2

10.2 Vector format conversion

  1. Convert the following vectors to rectangular (Cartesian) format without using a calculator (Hint: the angles are nice):
    1. \((4,0^{\circ}) \longrightarrow \begin{pmatrix}4\\0 \end{pmatrix}\)
    2. \((8,90^{\circ}) \longrightarrow \begin{pmatrix}0\\8 \end{pmatrix}\)
    3. \((6,180^{\circ}) \longrightarrow \begin{pmatrix}-6\\0 \end{pmatrix}\)
    4. \((5,270^{\circ}) \longrightarrow \begin{pmatrix}0\\-5 \end{pmatrix}\)
    5. \((3,-90^{\circ}) \longrightarrow \begin{pmatrix}0\\-3 \end{pmatrix}\)
    6. \((10,,-180^{\circ}) \longrightarrow \begin{pmatrix}-10\\0 \end{pmatrix}\)
  2. Convert the following vectors into rectangular (Cartesian) format with the aid of the standard equations (4.1), and then your calculator.
    1. \((2,30^{\circ}) \longrightarrow \begin{pmatrix}1.732 \\1 \end{pmatrix}\)
    2. \((3,80^{\circ}) \longrightarrow \begin{pmatrix}0.521\\2.954 \end{pmatrix}\)
    3. \((1,120^{\circ}) \longrightarrow \begin{pmatrix}-0.5\\0.866 \end{pmatrix}\)
    4. \((5,315^{\circ}) \longrightarrow \begin{pmatrix}3.536\\-3.536 \end{pmatrix}\)
    5. \((4,200^{\circ}) \longrightarrow \begin{pmatrix}-3.759\\-1.368 \end{pmatrix}\)
    6. \((2,-75^{\circ}) \longrightarrow \begin{pmatrix}0.518\\-1.932 \end{pmatrix}\)
  3. Convert the following vector to Polar format, without the use of a calculator (Hint: the angles will be nice)
    1. \(\begin{pmatrix}5 \\ 0 \end{pmatrix} \longrightarrow (5,0^{\circ})\)
    2. \(\begin{pmatrix}0 \\ 10 \end{pmatrix} \longrightarrow (10,90^{\circ})\)
    3. \(\begin{pmatrix}-8 \\ 0 \end{pmatrix} \longrightarrow (8,180^{\circ})\)
    4. \(\begin{pmatrix}0 \\ -2 \end{pmatrix} \longrightarrow (2,-90^{\circ}) \text{ or }(2,270^{\circ})\)
  4. Convert the following vectors from rectangular format to Polar format,
    1. \(\begin{pmatrix}-3 \\ 2 \end{pmatrix} \longrightarrow (3.606 ,146.310^{\circ})\)
    2. \(\begin{pmatrix}3 \\ -2 \end{pmatrix} \longrightarrow (3.606 ,-33.690^{\circ})\)
    3. \(\begin{pmatrix}-4 \\ -3 \end{pmatrix} \longrightarrow (5 ,-143.130^{\circ})\)
    4. \(\begin{pmatrix}4 \\ 3 \end{pmatrix} \longrightarrow (5 ,36.870^{\circ})\)
    5. \(\begin{pmatrix}-2 \\ 1 \end{pmatrix} \longrightarrow (2.236 ,153.435^{\circ})\)
    6. \(\begin{pmatrix}2 \\ -1 \end{pmatrix} \longrightarrow (2.236 ,-26.565^{\circ})\)

10.3 Vector addition, subtraction and multiplication

  1. Given the vectors \(\underline{v}_1= \begin{pmatrix}4\\ -3 \end{pmatrix}\), \(\underline{v}_2= \begin{pmatrix}-2 \\ 4 \end{pmatrix}\) and \(\underline{v}_3= \begin{pmatrix}-5 \\ -1\end{pmatrix}\), determine the following vectors. In cases (i)-(vi) you may like to sketch the answers graphically too.
    1. \(\underline{v}_1+\underline{v}_2= \begin{pmatrix}2 \\ 1 \end{pmatrix}\)
    2. \(\underline{v}_1+\underline{v}_2+\underline{v}_3= \begin{pmatrix}-3 \\ 0 \end{pmatrix}\)
    3. \(\underline{v}_1+(-\underline{v}_2)= \begin{pmatrix}6 \\ -7 \end{pmatrix}\)
    4. \(\underline{v}_1-\underline{v}_3= \begin{pmatrix}9 \\ -2 \end{pmatrix}\)
    5. \(2\underline{v}_1= \begin{pmatrix}8 \\ -6 \end{pmatrix}\)
    6. \(3\underline{v}_2= \begin{pmatrix}-6 \\ 12 \end{pmatrix}\)
    7. \(2\underline{v}_1+3\underline{v}_2= \begin{pmatrix}2 \\ 6 \end{pmatrix}\)
    8. \(4\underline{v}_1-2\underline{v}_2+5\underline{v}_3= \begin{pmatrix}-5 \\ -25 \end{pmatrix}\)

10.4 Scalar Products and Relative Positions

  1. For each of the following pairs of vectors, determine their lengths \(|\underline{v}_1|\), \(|\underline{v}_1|\), their Scalar Product (\(\underline{v}_1\cdot\underline{v}_2\)), and the angle between them, \(\theta\).
    1. \(\underline{v}_1 = \begin{pmatrix} 2 \\ 2 \end{pmatrix},\; \underline{v}_2 = \begin{pmatrix} 1 \\ -3 \end{pmatrix}\) \[ |\underline{v_1}|=\sqrt{8}, |\underline{v_2}|=\sqrt{10}, \underline{v_1}\cdot\underline{v_2}=-4 ,\theta= 116.57^{\circ}\]
    2. \(\underline{v}_1 = \begin{pmatrix} -4 \\ 6 \end{pmatrix},\; \underline{v}_2 = \begin{pmatrix} 5 \\ -8 \end{pmatrix}\) \[ |\underline{v_1}|=\sqrt{52}, |\underline{v_2}|=\sqrt{89}, \underline{v_1}\cdot\underline{v_2}=-68 ,\theta= 178.32^{\circ}\]
    3. \(\underline{v}_1 = \begin{pmatrix} 3 \\ 4 \end{pmatrix},\; \underline{v}_2 = \begin{pmatrix} 1 \\ 0 \end{pmatrix}\) \[ |\underline{v_1}|=5, |\underline{v_2}|=1, \underline{v_1}\cdot\underline{v_2}=3 ,\theta= 53.13^{\circ}\]
    4. \(\underline{v}_1 = \begin{pmatrix} 3 \\ 4 \end{pmatrix},\; \underline{v}_2 = \begin{pmatrix} 0 \\ 1 \end{pmatrix}\) \[ |\underline{v_1}|=5, |\underline{v_2}|=1, \underline{v_1}\cdot\underline{v_2}=4 ,\theta= 36.87^{\circ}\]
  2. A triangle has vertices \(A=(1,1)\), \(B=(4,2)\) and \(C=(3,4)\).
    1. Sketch this triangle on the standard \(xy\)-axes (including the origin).
    2. Determine the relative position vectors \(\overrightarrow{AB}\) and \(\overrightarrow{AC}\). \[\overrightarrow{AB}=\begin{pmatrix}3 \\ 1 \end{pmatrix}, \overrightarrow{AC}=\begin{pmatrix}2 \\ 3 \end{pmatrix}.\]
    3. By calculation (using a Scalar Product), determine the angle of the triangle at the vertex \(A\). \[ \theta = 37.9^{\circ}\]
    4. If you have access to a protractor, try measuring the angle in your diagram to see if it agrees.
  3. A triangle has vertices \(A=(-2,1)\), \(B=(3,1)\) and \(C=(1,5)\).
    1. Draw this triangle accurately (including the origin).
    2. By calculation (using a Scalar Product), determine the angle of the triangle at the vertex \(B\). \[ \theta=63.4^{\circ}\]
    3. If you have access to a protractor, try measuring the angle in your diagram to see if it agrees.

10.5 Scalar Product further applications

  1. For each of these pairs of vectors, determine whether the pair are orthogonal to each other (i.e. at right-angles): Vectors are orthogonal if and only if their Scalar Product is zero:
    1. \(\underline{v}_1 = \begin{pmatrix} 4 \\ 0 \end{pmatrix},\; \underline{v}_2 = \begin{pmatrix} 0 \\ 3 \end{pmatrix} \Longrightarrow \underline{v_1}\cdot\underline{v_2}=0 \Rightarrow \text{Orthogonal}\)
    2. \(\underline{v}_1 = \begin{pmatrix} 3 \\ 2 \end{pmatrix},\; \underline{v}_2 = \begin{pmatrix} -3 \\ 2 \end{pmatrix} \Longrightarrow \underline{v_1}\cdot\underline{v_2}=-5 \Rightarrow \text{Not orthogonal}\)
    3. \(\underline{v}_1 = \begin{pmatrix} 1 \\ 5 \end{pmatrix},\; \underline{v}_2 = \begin{pmatrix} -5 \\ 1 \end{pmatrix} \Longrightarrow \underline{v_1}\cdot\underline{v_2}=0 \Rightarrow \text{Orthogonal}\)
    4. \(\underline{v}_1 = \begin{pmatrix} 15 \\ 3 \end{pmatrix},\; \underline{v}_2 = \begin{pmatrix} -2 \\ 10 \end{pmatrix} \Longrightarrow \underline{v_1}\cdot\underline{v_2}=0 \Rightarrow \text{Orthogonal}\)
    5. \(\underline{v}_1 = \begin{pmatrix} 10 \\ 3 \end{pmatrix},\; \underline{v}_2 = \begin{pmatrix} -10 \\ 33 \end{pmatrix} \Longrightarrow \underline{v_1}\cdot\underline{v_2}=-1 \Rightarrow \text{Not orthogonal}\)
  2. For each of the following forces \(\underline{F}\) find the Scalar projection of \(\underline{F}\) in the direction of the given vector \(\underline{d}\): In each case we need to calculate \(\underline{F}\cdot\underline{\hat{d}}\) where \(\underline{\hat{d}}\) is a vector of length \(1\) in the direction of \(d\). In the first three examples \(\underline{\hat{d}}=\underline{d}\) is already of length \(1\). In the final case we need to divide by its length (which is \(5\))
    1. \(\underline{F} = \begin{pmatrix} 5 \\ 0 \end{pmatrix},\; \underline{d} = \begin{pmatrix} 1/\sqrt{2} \\ 1/\sqrt{2} \end{pmatrix} \Longrightarrow \underline{F}\cdot\underline{\hat{d}}=5/\sqrt{2}=3.536\)
    2. \(\underline{F} = \begin{pmatrix} 4 \\ -3 \end{pmatrix},\; \underline{d} = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \Longrightarrow \underline{F}\cdot\underline{\hat{d}}=-3\)
    3. \(\underline{F} = \begin{pmatrix} 3 \\ -2 \end{pmatrix},\; \underline{d} = \begin{pmatrix} 0.6 \\ 0.8 \end{pmatrix} \Longrightarrow \underline{F}\cdot\underline{\hat{d}}=0.2\)
    4. \(\underline{F} = \begin{pmatrix} 2 \\ 1 \end{pmatrix},\; \underline{d} = \begin{pmatrix} 3 \\ 4 \end{pmatrix} \Longrightarrow \underline{F}\cdot\underline{\hat{d}}=\frac{1}{5} 10 = 2\)
  3. For each of the following forces \(\underline{F}\) find the work done in moving an object from location \(P\) to location \(Q\): **In each case we need to calculate \(\underline{F}\cdot\overrightarrow{PQ}\)
    1. \(\underline{F} = \begin{pmatrix} 5 \\ 1 \end{pmatrix},\; P = (1,3), Q=(2,5) \Rightarrow \underline{F}\cdot\overrightarrow{PQ}=9\).
    2. \(\underline{F} = \begin{pmatrix} -1 \\ -1 \end{pmatrix},\; P = (1,3), Q=(-2,-5) \Rightarrow \underline{F}\cdot\overrightarrow{PQ}=11\).
    3. \(\underline{F} = \begin{pmatrix} 2 \\ 3 \end{pmatrix},\; P = (-6,-4), Q=(0,0) \Rightarrow \underline{F}\cdot\overrightarrow{PQ}=24\).

10.6 3-dimensional vectors (mixture of topics)

  1. Given the three 3-dimensional vectors \[\underline{v}_1= \begin{pmatrix}4\\ -5 \\1 \end{pmatrix},\; \underline{v}_2= \begin{pmatrix}5 \\ 6 \\-3 \end{pmatrix},\; \underline{v}_3= \begin{pmatrix}6 \\ 2 \\ -4 \end{pmatrix}\] determine the following:
    1. \(\underline{v}_1+\underline{v}_2+\underline{v}_3 = \begin{pmatrix}15 \\ 3 \\-6 \end{pmatrix}\)
    2. \(4\underline{v}_1+3\underline{v}_2-2\underline{v}_3 = \begin{pmatrix}19 \\ -6 \\ 3 \end{pmatrix}\)
    3. \(\underline{v}_1+(-\underline{v}_3) = \begin{pmatrix}-2 \\ -7 \\ -5 \end{pmatrix}\)
    4. \(-2\underline{v}_1+\underline{v}_2+5\underline{v}_3 = \begin{pmatrix}27 \\26 \\ -25 \end{pmatrix}\)
    5. \(\underline{v}_1\cdot\underline{v}_2 = -13\)
    6. \(\underline{v}_2\cdot\underline{v}_3 = 54\)
    7. \(\underline{v}_1\times \underline{v}_2 = \begin{pmatrix}9 \\ 17 \\ 49 \end{pmatrix}\)
    8. \(\underline{v}_2\times\underline{v}_3 = \begin{pmatrix}-18 \\ 2 \\ -26 \end{pmatrix}\)
    9. \(\underline{v}_3\times\underline{v}_2 = \begin{pmatrix}18 \\ -2 \\ 26 \end{pmatrix}\)
  2. Using the same vectors from the previous question, find the following: (you may use previous answers, to speed up calculations)
    1. The angle between \(\underline{v}_1\) and \(\underline{v}_2\) is \(\theta=103.87 ^{\circ}\).
    2. The angle between \(\underline{v}_1\) and \(\underline{v}_3\) is \(\theta=78.1 ^{\circ}\).
    3. The component/projection of \(\underline{v}_1\) in the direction of \(\underline{v}_2\) is \(-3.153\).
    4. The component/projection of \(\underline{v}_3\) in the direction of \(\underline{v}_1\) is \(1.543\).
  3. A triangle in 3D has vertices at \(A=(1,4,3)\), \(B=(4,2,0)\) and \(C=(5,4,6)\).
    1. Determine the relative position vectors \(\overrightarrow{AB}\) and \(\overrightarrow{AC}\). \[ \overrightarrow{AB}= \begin{pmatrix}3\\-2\\-3 \end{pmatrix}, \overrightarrow{AC}=\begin{pmatrix}4\\0\\3 \end{pmatrix}\]
    2. Determine the angle of the triangle at vertex \(A\). \[ \theta=82.65^{\circ}\]
  4. A triangle in 3D has vertices at \(A=(-2,3,-5)\), \(B=(2,0,4)\) and \(C=(1,5,1)\)
    1. Determine the angle of the triangle at vertex \(C\). \[ \theta=105.40^{\circ}\]

10.7 3D vector applications

  1. A force \(\underline{F}=\begin{pmatrix}3\\-2\\5\end{pmatrix}\) acts on a particle which moves from point \(P=(1,4,-1)\) to point \(Q=(-2,3,1)\).
    1. Determine the displacement vector \(\underline{d}\) of the particle. \[ \underline{d} = \overrightarrow{PQ}=\begin{pmatrix}-3\\-1\\2 \end{pmatrix}\]
    2. Determine the work done by the force. \[ \text{Work done}=\underline{F}\cdot\underline{d} = 3.\]
  2. A force \(\underline{F}\) acts through a point \(P\). Given that \(P=(2,3,-5)\), \(Q=(1,2,-3)\) and \(\underline{F}=\begin{pmatrix}3\\-2\\5\end{pmatrix}\),
    1. Calculate the moment of this force about the point \(Q\). You may want to consult Section 4.14.2. \[ \text{Moment of force}=\underline{M}=\underline{r}\times\underline{F} = \begin{pmatrix}-8\\6\\-1 \end{pmatrix}\] A moment/torque produces a rotation. The direction of this vector gives the direction of the axis of that rotation. The length is the strength of the force.