Wk 6



  • Deflection of Beams

    This topic deals with the deflection of beams. We have already studied beams by considering the calculation of reaction forces so that we can draw the variation of shear forces and bending moments along the span of a beam. We also studied different types of beams (simply-supported, cantilevers) and beam supports (knife edges, rollers, pins and fixed ends).

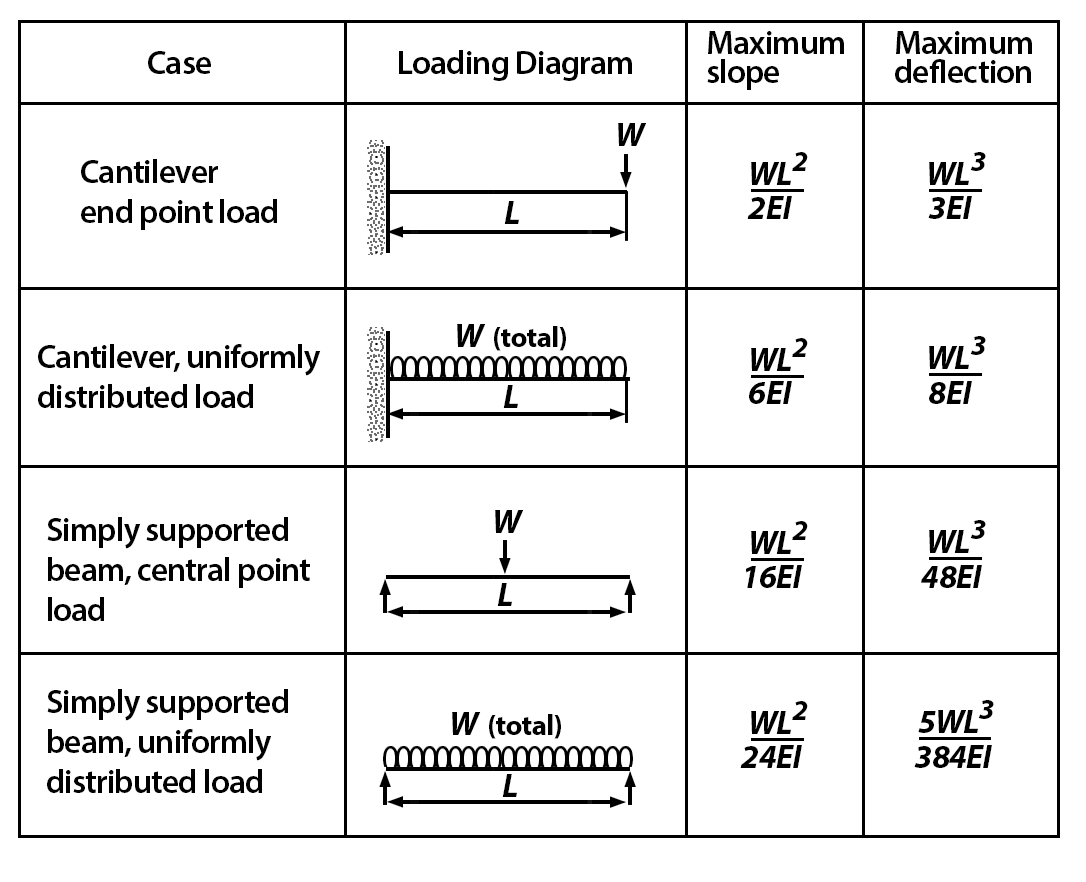
    It is also of great interest to be able to calculate the deflection of a beam under external loading and to indentify the point along the span of a beam where the maximum deflection occurs. We will study 'standard' beam cases using a direct integration method, and 'non-standard' beams using Macaulay's method.

  • Theory of Deflection of Beams – Standard Beam Cases

    📷 Table 1 shows max slope and maximum deflection equations for standard beams and cantilevers where L = total length (m) and W = total load (N). [All derived from Eq(3).] For distributed load cases, W = wL (N), where w = load per unit length (N/m). - click to view

    Deflection of Beams – Non-Standard Cases: Macauley’s Method

    The simple integration method used above can only be used when a single expression for BM applies along the complete length of a beam.

    In general, this is not the case, and a method has to be adapted to cover all loading conditions – one such method is Macaulay’s Method.

    Consider the simply supported beam with a concentrated off-centre load as shown.
    📷 View Diagram Larger

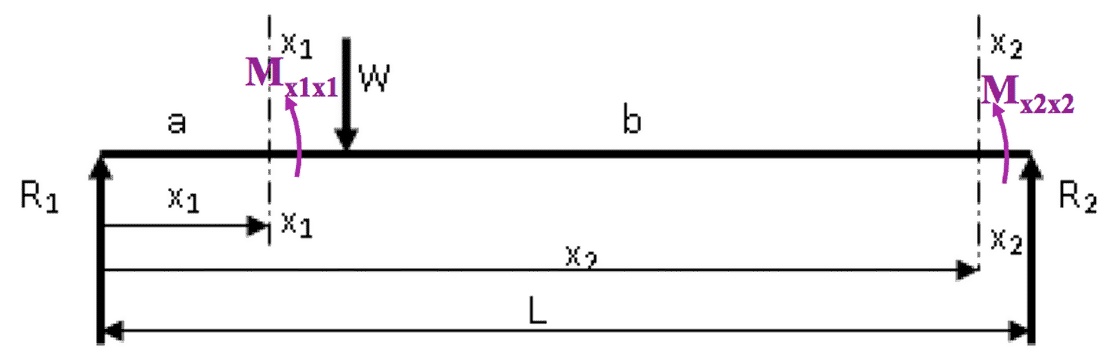
    Consider section x1x1: Mx1x1 = R1x1 and is valid for 0 < x < a.

    Consider section x2x2: Mx2x2 = R1x2 – W(x2 - a) and is valid for a < x < L.
    In order to use the elastic beam deflection equation $ \large EI \frac{d^2y}{dx^2} = - M _{xx} $
    The expression for M must hold for any section x-x from x = 0 to x = L.

    It is necessary to ignore the term containing the bracket when the quantity within the bracket becomes negative, i.e. when x < a, (x – a) is negative and should be ignored.
    Hence, Mxx = R1x – W(x – a) can be considered to be a general equation for the bending moment at any section along the beam.

    Continues on next tab.



    Deflection of Beams

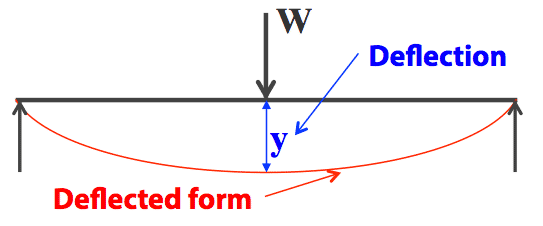
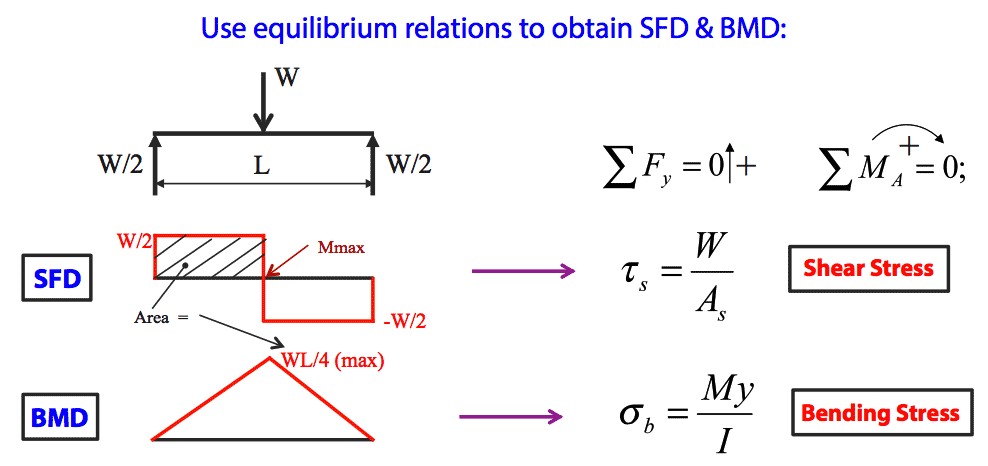
    Previously we have seen that the loading actions at any section of a simply-supported beam or a cantilever can be resolved into a bending moment and a shearing force, and diagrams showing how they vary with respect to beam length were drawn. 📷 Methods of calculating stresses due to these bending moments and shearing forces have also been studied, eg., standard simply-supported beam with a mid-span point load: - click to view

    There is another aspect of the problem of bending which must also be considered, namely, the calculation of the stiffness of the beam and hence the deflection.

    A beam should not only be strong enough for its purpose (to support loads), but also that it should not deflect from its original position by more than a certain (small) amount (basis of elastic behaviour).

    It is therefore necessary that we are able to find the deflected form of the beam under a known system of external loads with known support conditions.



  • Typical Applications of Macauley’s Method.
     ii) Beam with partially distributed uniform loading:
    📷 View Diagram Larger
      From the loaded beam above:
    $$ \large M _{xx} = R_1 x - w (b - a) \Bigg[ x - a - \frac{(b - a)}{2} \Bigg] \; \; \small \color{red}{\text{Eq (A)}} $$
    This is expression is difficult to integrate and hence it is more usual to make use of the principle of superposition, as follows:
    📷 View Diagram Larger
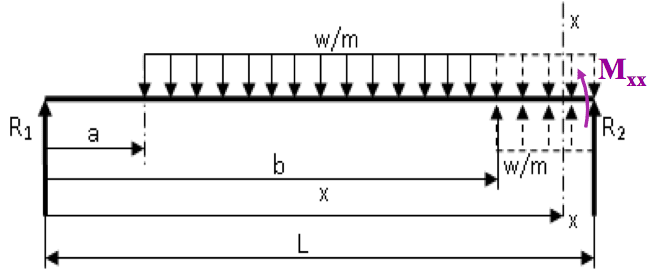      From the same loaded beam above:
    $$ \large M _{xx} = R_1 x - \frac{w}{2} (x - a)^2 + \frac{w}{2} (x - b)^2 \; \; \small \color{red}{\text{Eq (B)}} $$
    $ \color{red}{\text{Eq (B)}} $ is easier to integrate and is therefore preferred – when $ \color{red}{\text{Eq (A)}} $ is multiplied out, it will = $ \color{red}{\text{Eq (B)}}$ !

    ⬇ Beam Deflection Worked Example 1
    ⬇ Beam Deflection Worked Example 2


    Deflection of Beams – Non-Standard Cases: Macauley’s Method (cont.)

    📷 View Diagram Larger
    Rules for Macaulay’s Method:
    - Take the origin at either left or right hand extremity and section x-x just preceeding the last force action at the other end.
    - Express Mxx in terms of distances from the origin.
    - Substitute into $ \large EI \frac{d^2y}{dx^2} = - M _{xx} $ and integrate keeping all bracket terms intact.
    - When evaluating the constants of integration, slope or deflection, any term for which the quantity within the brackets becomes negative is discarded.

    Typical Applications of Macauley’s Method.
     i) Beam with bending moment concentrated at one point
    📷 View Diagram Larger
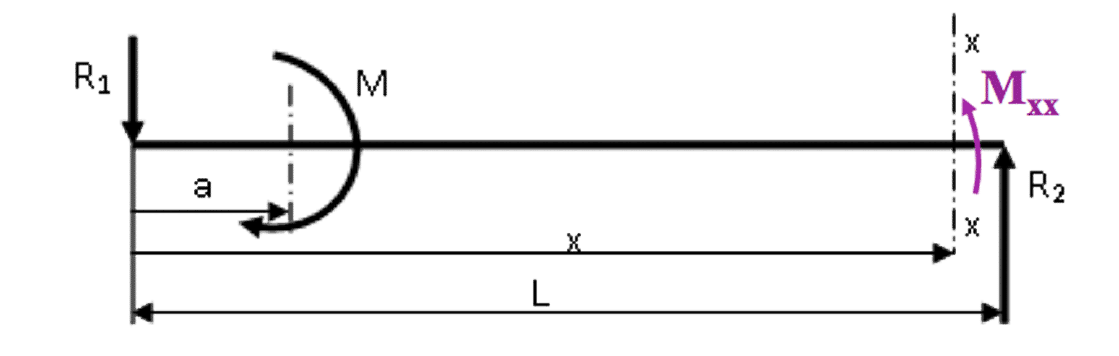
    If an applied moment M acts on the beam at any point other than the ends, then the distance ‘a’ from the origin must be included in the expression for Mxx. This is achieved by using the mathematical statement that any number raised to the power 0 (zero) is unity. $$ \large \textit{i.e.} M_{xx} = - R_1x + M (x-a)^0 $$ and if (x-a) term becomes negative, i.e. (0 < x < a), then the whole term M(x-a) is ignored.





  • Tutorials

    ⬇ Beam Deflection Tutorial